空心板梁桥铰缝破坏机理精细化有限元分析

高庆飞， 宋洪雨，2， 张 坤， 秦卫军

(1.哈尔滨工业大学 交通科学与工程学院， 黑龙江 哈尔滨 150090； 2.北京市市政工程设计研究总院有限公司， 北京 100082； 3.吉林省交通科学研究所， 吉林 长春 130012)

0 引言

空心板梁桥由于其构造简单、建筑高度低、施工方便、造价低等优势在我国中小跨径桥梁中得到了广泛应用[1]。但是大量空心板梁桥都在运营期间出现病害，随后国家颁布了2008年交通部空心板标准图以改进企口缝的构造设计，不过改进并没有彻底克服病害问题，铰缝病害仍然严重影响着桥梁的安全性和耐久性[2-4]。作为空心板梁桥的结构整体受力关键构件，铰缝存在着某些先天不足从而使其成为结构体系中的最薄弱的构件，一旦发生病害，不仅是严重的安全隐患，而且增加了大量养护维修成本，因此研究铰缝的受力状态及其破坏机理变得尤为重要，为接下来的病害防治养护加固等提供重要理论支持[5-8]。

我国现行的空心板梁桥设计方法采用铰接板法计算横向分布影响线，在最不利布载下计算出合板梁的横向分布系数，根据单梁最大荷载进行截面配筋设计，根据等效半波荷载峰值求出接缝内最大剪力，最后按照纯剪状态验算铰缝剪力[9-10]。

1 荷载横向分布研究

1.1 有限元法计算横向分布

铰缝将车辆荷载传递到各板梁上，采用横向分布理论简化桥梁实际受力，对简化后的平面问题进行计算。铰接板法假定铰缝无横向抗弯刚度，仅传递竖向剪力，实际中铰缝的自由转动被限制，能够传递弯矩，故需采用有限元法建立实体模型来模拟铰缝实际情况。

参考2008年交通部13m跨径装配式先张法预应力混凝土简支空心板梁标准图(公路-I级)，利用ANSYS大型有限元软件，采用Solid45实体单元模拟铰缝及空心板，不考虑普通钢筋及预应力钢绞线，不考虑桥面铺装层取最不利情况，10块板有限元模型见图1。

图1 10块板有限元模型

计算得到10块板模型横向分布影响线有限元法计算结果见图2，结构高度对称，因此仅给出桥梁一半结果。

图2显示，大铰缝空心板梁桥荷载梁间分布更均匀，大铰缝在铰缝完好时，空心板梁整体受力性能较好，小铰缝横向联系弱，荷载横向传递较差。

1.2 铰接板法计算横向分布

将空心板截面特性代入式(1)中求出刚度参数，截面特性见表1，计算横向分布影响线坐标值，绘制荷载横向分布影响线，10块板模型横向分布影响线铰接板法计算结果见图3。

图2 10块板模型横向分布影响线有限元法计算结果

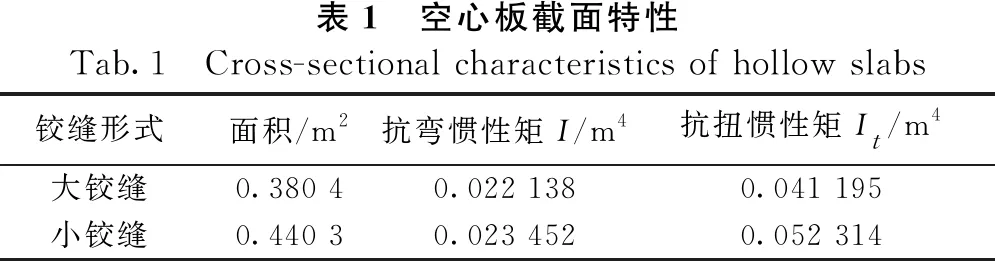
表1 空心板截面特性Tab.1 Cross-sectional characteristics of hollow slabs铰缝形式面积/m2抗弯惯性矩I/m4抗扭惯性矩It/m4大铰缝0.380 40.022 1380.041 195小铰缝0.440 30.023 4520.052 314

(1)

图3显示，有限元法相比铰接板法计算结果更加均匀、整体性好，且随着板数的增加，荷载分布的不均匀程度更加明显。

1.3 横向分布对比分析

为了更直观分析，将刚接板法、铰接板法、铰缝完好和大铰缝开裂一定高度的有限元法的计算结果分别进行比较，刚接板法考虑横向弯矩的影响。

a.大铰缝空心板梁桥。

分析大铰缝空心板梁桥横向分布，对比铰缝不同开裂高度模型有限元计算结果，显示随铰缝开裂高度增加，荷载横向分布逐渐趋近铰接板法计算结果，以铰缝开裂31 cm为例，给出大铰缝1号板梁横向分布影响线对比结果，见图4。

图3 10块板模型横向分布影响线铰接板法计算结果

对比可以看出，大铰缝空心板梁桥，其铰缝完好时，有限元法和刚接板法计算结果接近，说明铰缝完好时，大铰缝空心板梁桥受力状态接近整体板，其铰缝开裂到一定程度时，各板梁间横向联系减弱，计算结果接近铰接板法，不过仍存在一定差距。结果显示，铰接板法理论与大铰缝空心板梁实际情况存在一定差异，单就主梁设计看，计算结果偏于保守。

图4 大铰缝1号板梁横向分布影响线对比

b.小铰缝空心板梁桥。

在2008年交通部空心板梁标准图发布之前，我国主要采用小铰缝形式空心板梁桥，运用上述分析方法，对小铰缝空心板梁桥的荷载横向分布进行分析，对比大铰缝空心板梁桥研究铰缝病害产生原因，小铰缝1号板梁横向分布影响线对比结果，见图5。

图5显示，小铰缝空心板梁桥，有限元法与铰接板法计算结果接近，小铰缝空心板模型整体性不如大铰缝空心板好，铰接板法计算结果更接近实际受力，但由于铰缝多边形构造限制自由转动，依然和实际情况存在一定差异。

图5 小铰缝1号板梁横向分布影响线对比

以上采用不同方法对比分析了空心板梁桥的荷载横向分布规律，不同方法计算所得的结果存在较大差异，现行设计规范中铰接板法不能精确反应大铰缝空心板梁桥实际荷载横向分布，为分析铰缝病害机理，需针对铰缝应力状态进一步研究。

2 空心板铰缝应力分布

2.1 最不利布载

现行空心板梁桥的设计主要采用大铰缝构造形式，大铰缝板间横向联系较强，实际运营时更接近板的形式，然而对于铰缝病害产生的原因，需要分析铰缝的实际受力状态。

建立5块板有限元模型，分9个工况进行加载，观察铰缝截面各控制点应力状态，分析不同工况下铰缝位置的应力分布，工况加载位置及铰缝应力控制点位置见图6，参考《公路桥涵设计通用规范》(JTG D60-2015)采用车轮均布荷载形式，荷载取200 kN，车轮桥面的接触面积为0.6 m×0.2 m，不考虑桥面铺装。

2.2 横向正应力

取铰缝底缘1#控制点，分析不同荷载工况下空心板梁桥的铰缝横向正应力分布，横向正应力沿纵向分布规律见图7。

图6 各工况加载位置及铰缝应力控制点位置

图7显示，靠近荷载布置位置的铰缝底缘横向拉应力较为集中，远离荷载布置位置的铰缝底缘出现横向压应力。1号铰缝底缘在中板跨中布载时产生最大横向正应力，取其所在铰缝截面分析，采用工况1进行加载，提取1#控制点→3#控制点→6#控制点横向正应力沿竖向分布规律，与整体板进行对比。

整体空心板铰缝可以与主梁看作整体，铰缝作为受力构件上缘受压，底缘受拉，接近横向受弯构件，由于构造本身原因，铰缝底缘出现最大横向正应力。1号铰缝顶缘出现少量横向拉应力，理论上不应该出现，对铰缝顶缘横向正应力沿桥梁纵向分布进行分析，见图8。

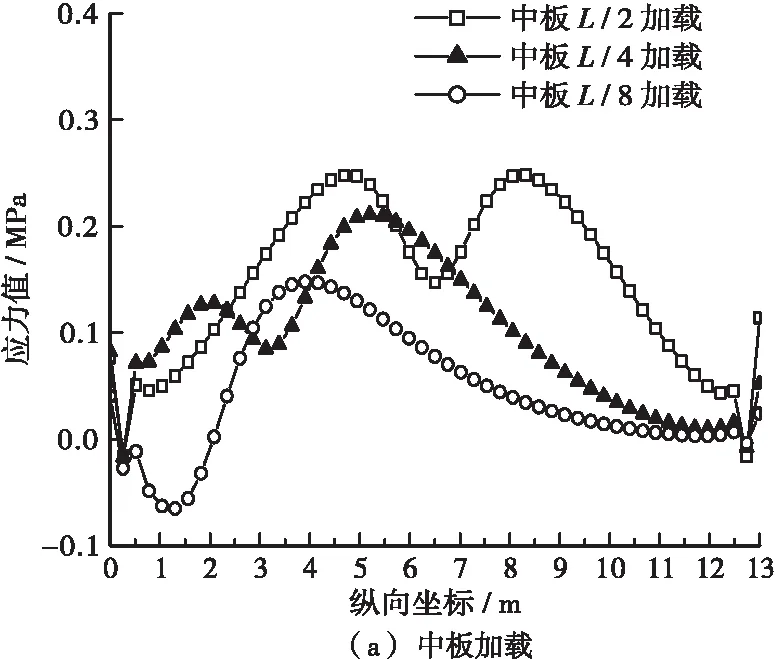
图7 1号铰缝底缘横向正应力沿纵向分布

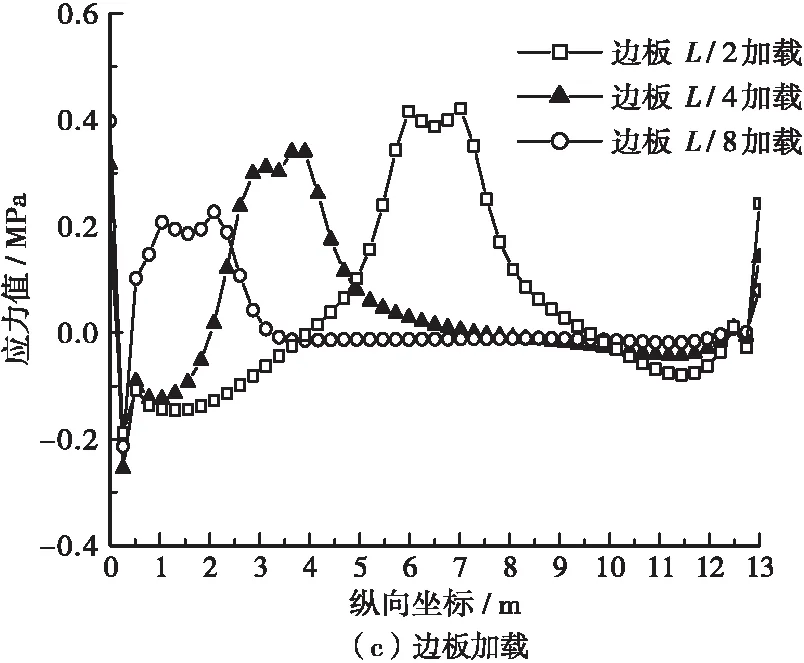
续图7 1号铰缝底缘横向正应力沿纵向分布

加载区附近铰缝顶缘局部拉应力突变，在边板加载时达到最大，局部应力集中导致了突变，在消除应力集中后铰缝顶缘则恢复了受压性能。

将9块板模型与5块板模型的横向正应力最大值及最大值所在截面沿铰缝高度规律进行对比，分析桥宽对横向正应力分布影响。结果显示桥宽并不影响横向正应力沿铰缝高度的分布规律，铰缝底缘最大横向拉应力随桥宽增加变大。采用此法研究小铰缝空心板梁桥，发现小铰缝沿高度方向处于受压状态，铰缝底缘存在较大横向拉应力，在中板跨中布载下2号铰缝底缘横向正应力沿铰缝高度分布及纵向分布规律，见图9。

图8 1号铰缝顶缘横向正应力沿纵向分布

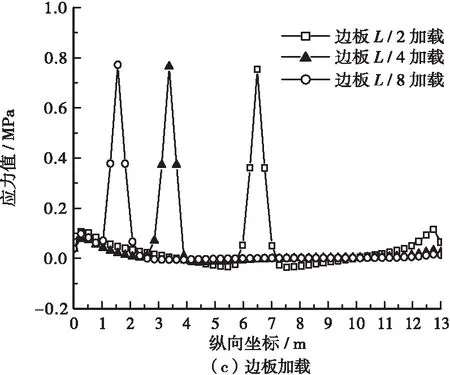
续图8 1号铰缝顶缘横向正应力沿纵向分布

图9 小铰缝横向正应力沿铰缝高度分布及纵向分布

图9显示，加载区附近铰缝底缘存在局部低应力区，横向正应力水平整体比大铰缝要高。取铰缝底部完全填充、小铰缝、大铰缝的空心板模型研究，采用工况1布载，对比后分析2号铰缝底缘横向正应力以及中板和次边板产生的横向位移规律。横向正应力对比见图10，横向位移及位移差对比见图11。

图10、图11显示，横向位移差和横向正应力的分布规律基本一致，因此相邻板梁的横向相对位移是导致铰缝底缘横向正应力的主要原因。为实现相邻板梁间的变形协调，装配式空心板梁桥浇筑铰缝时留1 cm施工缝，荷载较大时，板梁受力扭转，板梁间出现横向相对位移，产生横向正应力，随着铰缝高度的变小，横向连接变差，各板梁自由活动空间变大，在铰缝底缘产生较大横向拉应力，而全部填充的铰缝底部由于变形协调均匀，横向正应力较小。

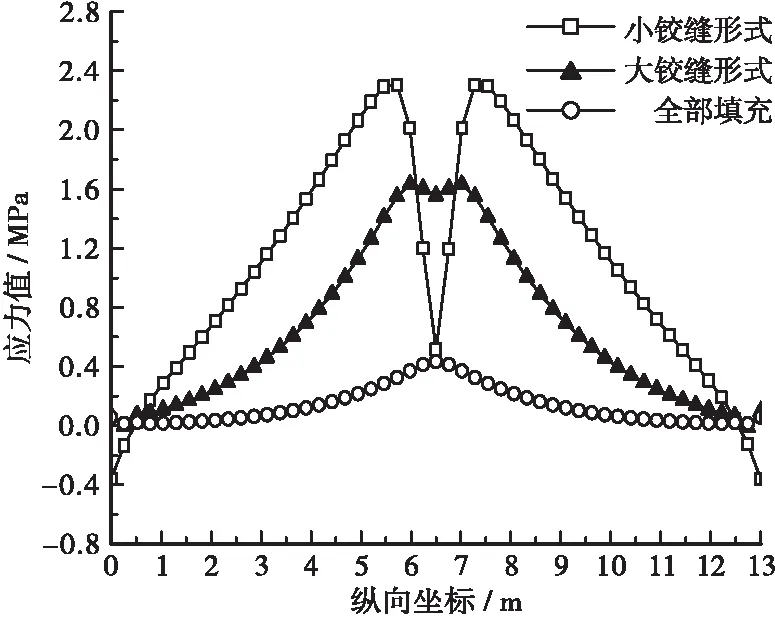
图10 铰缝横向正应力分布对比

图11 铰缝相邻板梁横向位移对比

2.3 竖向剪应力

现行空心板设计中铰缝应力主要考虑竖向剪应力，现取在铰缝高度方向的竖向剪应力进行纵向分析，对空心板各铰缝在不同加载工况下竖向剪应力纵向分布进行比较，见图12。

图12 1号铰缝底缘竖向剪应力沿纵向分布

图12显示，铰缝竖向剪应力随着荷载距离的增大而快速衰减，支座附近也存在部分竖向剪应力，与9块板模型进行对比，竖向剪应力峰值不随桥宽改变而改变，铺装层可以使荷载均匀作业在各板梁从而分担部分荷载。

采用此法研究小铰缝高度对竖向剪应力的影响，小铰缝全截面抗剪，铰缝底缘峰值大于大铰缝的峰值，竖向剪应力沿纵桥向衰减规律与大铰缝一致，支座附近存在较大竖向剪应力，竖向剪应力沿铰缝高度分布及桥长方向分布规律见图13。

图13 小铰缝底缘竖向剪应力沿铰缝高度分布及沿桥长方向分布

2.4 纵向正应力

对比各工况布载下铰缝高度对纵向正应力的影响，发现铰缝沿纵向分布符合受弯构件规律，顶缘受压，底缘受拉，即在铰缝完好时，铰缝与主梁共同承担纵向弯矩。

铰缝底缘在纵向受弯时受拉，可能开裂，需要确定最大纵向正应力的出现位置，取铰缝底缘，分析纵向正应力在不同工况布载下沿桥梁纵向分布规律，见图14。

图14显示，铰缝纵向正应力随着远离荷载作用区域而变得平缓，与9块板模型进行对比，随桥宽增加纵向正应力峰值降低了，分析铺装层影响，增加10 cm混凝土铺装层可以有效减小铰缝纵向正应力峰值。

采用此法研究小铰缝高度对纵向正应力影响，由于小铰缝位于空心板中性轴以上，铰缝全截面在纵向受弯时处于受压区，因此纵向正应力并不直接导致小铰缝开裂，在中板跨中布载下2号铰缝底缘纵向正应力沿铰缝高度分布及桥长方向分布规律，见图15。

2.5 纵向剪应力

板梁间纵向错动会在铰缝位置产生纵向剪应力，铰缝底缘纵向剪应力在不同加载工况下沿纵桥向分布规律，见图16。

图16显示，铰缝底缘纵向剪应力随荷载向边板靠近而增大，采用此法研究小铰缝模型，纵向剪应力沿纵桥向分布规律与大铰缝一致，纵向剪应力沿铰缝高度分布及桥长方向分布规律见图17。

图14 1号铰缝底缘纵向正应力沿纵向分布

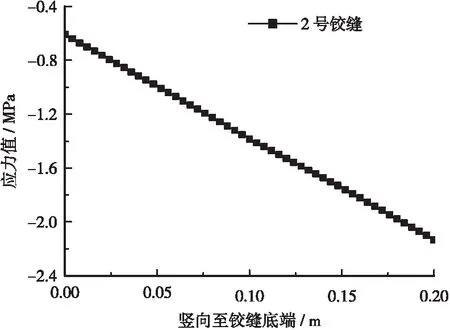
图15 小铰缝底缘纵向正应力沿铰缝高度分布及沿桥长方向分布

图16 1号铰缝底缘纵向剪应力沿纵向分布

图17 小铰缝底缘纵向剪应力沿铰缝高度分布及沿桥长方向分布

3 结论

通过建立空心板梁桥ANSYS有限元实体模型，对比分析了铰接板法与有限元法荷载横向分布影响线，研究了铰缝主要应力分布规律并依此分析了铰缝的实际受力状态。

a.大铰缝空心板梁桥中，当铰缝完好时，有限元法与刚接板法计算出的横向分布影响线结果较为接近，与铰接板法结果有许多差异，而当铰缝开裂至一定高度时，有限元法与铰接板法计算出的横向分布影响线结果较为接近。小铰缝空心板梁桥中，有限元法和铰接板法计算出的横向分布影响线结果更接近，但是存在一定差距。

b.铰缝实际受力状态十分复杂，现行设计方法不能完好地模拟，各主要应力的峰值存在于不同的工况之中，最不利荷载工况为中板跨中布载时，铰缝底缘横向正应力较大，而当纵向正应力和竖向剪应力达到一定水平后，铰缝底缘双向受拉，极易开裂。

c.铰缝的纵向正应力随桥宽增加逐渐减小，而横向正应力逐渐增大，从而成为铰缝产生病害的主要因素，铰缝底缘出现横向正应力的主要原因是相邻板梁的横向相对错动。

空心板梁存在施工接缝，在铰缝底缘存在较大应力，在交通荷载作用下铰缝开裂，随着裂缝不断发展，相邻板梁横向约束减弱，于是产生更大横向相对错动，由此又增大铰缝未开裂部分的横向拉应力，循环多次后，开裂至一定高度，铰缝由于抗剪不足被破坏，桥梁单板受力，安全性能降低。桥梁宽度的逐渐增大，会导致铰缝的纵向正应力减小、横向正应力增大，从而成为铰缝病害的主导因素。