室内自校准导航定位方法

傅惠民， 崔 轶

（北京航空航天大学 小样本技术研究中心， 北京 100191）

0 引言

据统计，人有80%左右时间是在室内活动[1]，因此室内导航定位具有广泛的应用前景。关于室内定位问题，目前已经发展了WiFi、蓝牙、超宽带、紫蜂、红外等一系列室内定位技术，但是，在非视距环境中的定位精度还有待进一步提高。 为此，本文提出一种室内信号强度路径损耗自校准模型， 与传统的因墙壁等障碍物引起的信号强度路径损耗模型相比， 本文的自校准模型既不需要大量试验，而且精度还更高。 在此基础上，建立了距离量测方程，给出一种基于接收信号强度指示（RSSI）的室内高精度定位方法。

关于室内导航问题， 由于用于室内导航的惯性导航系统往往存在较大漂移，不能很好地满足比室外导航精度更高的室内导航的要求。 为了解决上述问题，人们提出了行 人 航 位 推 算 方 法[2，3]，其 中 最 著 名 的 是Weinberg 模 型[4]，该模型以步态周期内Z 轴加速度的极差为特征量估计步长，其具体计算公式如下：式中：L 为步长，azmax和azmin分别为步态周期内Z 轴加速度的最大值和最小值，K 为步长参数， 可以通过训练得到。 但是Weinberg 模型存在两个不足，一是需要通过大量训练才能得到步长参数K， 这严重限制了它的实际使用；二是当室内地面不平（如上下坡或上下楼等）时，采用Z 轴加速度会导致步长误差。 对此，本文提出一种新的步长估计模型，并建立一种基于RSSI 的室内自校准导航方法，能够通过自校准滤波对步长参数进行实时估计，解决了传统方法需通过大量训练来确定参数的问题。

1 室内信号强度路径损耗自校准模型及方法

1.1 自校准模型

设在位置（x，y）处能够接收到n 个信号，其信号强度与距离之间的关系可用式（2）描述：

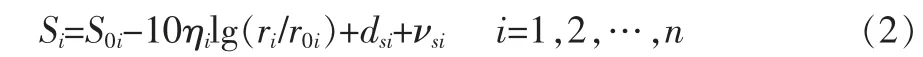
式中，Si为第i 个热点（AP）在距离ri处的信号强度，r0i为参考距离，S0i为参考距离处的信号强度，ηi为信号强度的路径损耗系数，在不同建筑物中有不同的取值，νsi为零均值的正态随机变量，即νsi～N（0，2σsi），dsi为因墙壁等障碍物引起的信号损耗而带来的未知输入 （未知的系统误差）。设前n0（n0≥3） 个信号是在视距环境中传播， 此时可取dsi=0，i=1，2， …，n0； 后n-n0个信号是在非视距环境中传播，如需穿过墙壁等障碍物，此时dsi一般不为零。

1.2 自校准方法

下面给出室内信号强度路径损耗自校准模型式（2）中未知输入dsi的自校准估计方法。 设第i 个AP 的位置坐标为（Xi，Yi），i=1，2，…，n，则有

实际工作中， 当不知道哪些信号是在视距环境中传播，哪些是在非视距环境中传播时，通常可将信号强度最大的前三个信号看作是在视距环境中传播。

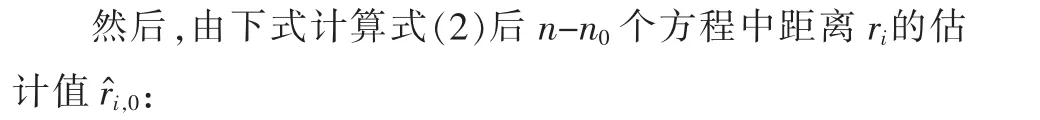
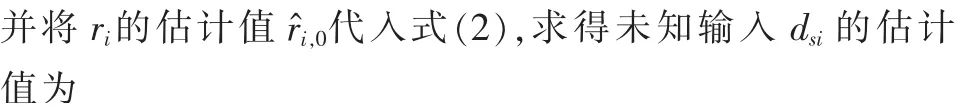
传统的因墙壁等障碍物引起的信号强度路径损耗模型比较复杂，其参数确定需要进行大量试验，而且精度也远没有式（2）的信号强度路径损耗自校准模型高。

2 基于RSSI 的室内自校准定位方法

2.1 距离量测方程

由式（2）可知，距离越远，距离估计值的分散性就越大，因此建立距离量测方程为

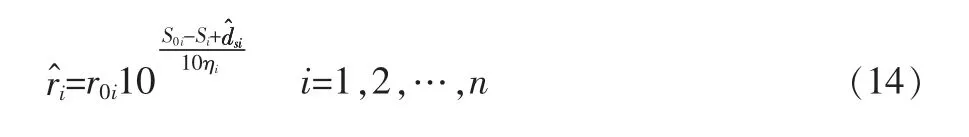
距离量测方程式（12）考虑了测量的随机性，所以能够比传统的距离方程更好地描述实际情况。

2.2 距离量测方程快速求解方法

3 新步长模型及行人航位自校准推算方法

3.1 一种新的步长估计模型

当室内地面不平（如上下坡或上下楼等）时，通过式（1）估计步长往往会产生较大的误差。 为此，本文提出一种新的步长估计模型：

式中：L 为步长，axmax和axmin分别为步态周期内X 轴加速度的最大值和最小值，aymax和aymin分别为步态周期内Y轴加速度的最大值和最小值，K 为步长参数，可以通过训练得到，也可以通过自校准滤波实时估计。

由于式（23）所示的步长估计模型是以水平方向加速度的极差为特征量，并未用到竖直方向的加速度，所以其不受路面坡度的影响， 能够在行人上下坡或上下楼时依然保持高精度的步长估计。

3.2 基于新步长模型的行人航位自校准推算方法

下面基于新的步长估计模型， 采用惯性传感器中陀螺仪和加速度计的量测数据， 给出一种行人航位自校准推算方法， 这里的自校准主要是对陀螺仪和加速度计的漂移进行校准。

首先，由式（24）计算总加速度：

式 中，acx，k，acy，k，acz，k为 第k 次 采 样 时 加 速 度 计 的 量 测 数据，ac，k为相应的总加速度。

实时对总加速度进行探测， 每探测到总加速度出现一个波峰，就代表行人迈出了一步。 同时，为了剔除伪波峰，设定如下两个阈值：

式中：a*为总加速度阈值，tc，k为第k 次采样距上一个总加速度波峰（真波峰）的时间间隔，t*为时间间隔阈值。 只有同时满足式（25）和式（26）的总加速度波峰，才被认为是真波峰。

与此同时，根据惯性导航方程，并通过对陀螺仪和加速度计量测数据进行自校准滤波处理， 实时计算行人的航向角。 滤波的状态方程如下式所示：

式中：ψk为航向角，θk为俯仰角，γk为滚转角，ωx，k，ωy，k，ωz，k为载体坐标系下的三轴角速度，△tk-1是相邻两次采样的时 间 间 隔，wψ，k-1，wθ，k-1，wγ，k-1，wωx，k-1，wωy，k-1，wωz，k-1为 状 态 噪声，bψ，k-1，bθ，k-1，bγ，k-1，bωx，k-1，bωy，k-1，bωz，k-1为状 态方 程 中的 未知输入。

滤波的量测方程由式（28）给出：

式中：ωgx，k，ωgy，k，ωgz，k为第k 次采样时陀螺仪的量测数据，νax，k，νay，k，νaz，k，νωx，k，νωy，k，νωz，k为量测噪声，dax，k，day，k，daz，k为量测方程中的未知输入，g 为当地的重力加速度，Cij，k为Ck矩阵第i 行第j 列的元素，Ck矩阵由式（29）计算。

采用文献[5]中的非线性系统双未知输入自校准滤波方法进行滤波， 也可以采用其中的两步自校准滤波方法来进一步提高滤波的鲁棒性和精度。第k 步滤波完成后，再由式（30）和式（31）计算水平方向的加速度。

当探测到行人迈出了一步时，即可由式（23）计算该步步长，进而由式（32）和式（33）估计行人所处的位置。

式中：（xj，yj）为第j 步终点的位置坐标，Lj为第j 步步长，ψj为第j 步内航向角的平均值。

4 基于RSSI 的室内自校准导航方法

下面将行人航位自校准推算和室内信号强度路径损耗自校准模型相结合，建立一种基于RSSI 的室内自校准导航方法，以进一步提高导航精度。

首先，由行人航位自校准推算式（32）和式（33），可得到基于RSSI 的室内自校准导航的状态方程为：

式中：Si，j为在第j 步终点（xj，yj）处来自第i 个AP 的信号强度，dsi，j为量测方程中的未知输入，νsi，j为量测噪声。 当第i 个AP 发出的信号在视距环境中传播时，直接令dsi，j=0，且这样的AP 不少于2 个。

最后，采用文献[5]中的非线性系统双未知输入自校准滤波方法对式（34）和式（36）进行导航滤波。 其中自校准主要是对步长模型式（23）中的参数即式（34）中的Kj-1和式（36）中的未知输入dsi，j进行实时校准和估计。

5 实例

现在北京航空航天大学新主楼20m×30m 的一个长方形走廊内的四个角和四条边中点布置了8 个WiFi AP。 行人手持手机沿长方形走廊行走一圈， 实时记录陀螺仪、 加速度计数据和接收到的每个WiFi AP 的三个信号强度平均值。

采用本文方法（新步长模型+自校准滤波）和传统方法 （Weinberg 模型+扩展卡尔曼滤波） 以及Weinberg 模型+自校准滤波方法进行计算。计算每一步终点的导航精度，并计算其平均值列于表1。

表1 平均导航精度比较

从表1 可以看到，本文方法的导航精度最高，比传统方法的导航精度提高了3.8 倍。 本文方法的导航精度比Weinberg 模型+自校准滤波方法的导航精度提高了25%，这说明本文提出的新步长模型在平地上也比Weinberg模型具有更高的精度。 此外，Weinberg 模型+自校准滤波方法的导航精度则比传统方法的导航精度提高了2.8倍， 这说明本文自校准滤波方法能够比传统扩展卡尔曼滤波方法显著提高导航精度。

6 结论

（1）本文的室内信号强度路径损耗自校准模型，能够根据信号强度的量测值实时进行自校准，具有精度高、实时性强的特点， 解决了传统的因墙壁等障碍物引起的信号强度路径损耗模型需要大量试验且精度不高的问题。

（2）推导出距离量测方程的协方差矩阵，建立了距离量测方程，因其考虑了测量的随机性，所以能够比传统的距离方程更加准确地描述实际情况。在此基础上，建立基于RSSI 的室内自校准定位方法，能够进行高精度定位。

（3）提出一种新的步长估计模型，它不但克服了传统的Weinberg 步长估计模型因地面不平导致的较大步长误差，而且在平地上也比Weinberg 模型具有更高的精度。

（4）给出行人航位自校准推算方法，通过对陀螺仪和加速度计的漂移进行自校准，有效地减小导航误差。

（5）建立基于RSSI 的室内自校准导航方法，通过将行人航位自校准推算和RSSI 自校准模型有机相结合，并通过自校准滤波对步长参数实时估计， 解决了传统方法需大量训练来确定参数的问题，显著提高导航精度。