基于多节点姿态信息融合的行人步长估计算法

欧 毅，张泽欣，李星海，曹加昇，刘 宇

（1.重庆邮电大学 智能传感技术与微系统重庆市高校工程研究中心，重庆 400065；2.中国科学院微电子研究所 集成电路先导工艺研发中心，北京 100029；3.中电科技集团 重庆声光电有限公司，重庆 401332）

随着社会经济的发展，人类活动越来越多地集中在室内，对室内定位的需求逐渐提高。目前常见的室内定位技术有WiFi定位［1-2］、RFID定位［3］、蓝牙定位［4-5］等。这些定位技术需要在室内提前布置基站、成本较高，且无法完成突发情况下的快速定位［6］。而行人惯性导航定位技术是一种自主式定位技术，仅依靠安装在行人身上的惯性测量单元即可获得行人位置信息，具有自主性强、不受外界环境干扰的特点［7-10］。其中行人步长估计是行人惯性定位算法中的关键技术，高精度的步长信息可以有效地提升定位算法精度。

为提升行人惯性定位算法中步长估计的精度，研究人员进行了大量研究。Martinelli等［11］提出了一种基于行为识别的步长估计算法，该算法可以根据测试人员运动状态的变化动态调整步长估计模型，但是需要先通过RVM对运动行为进行判断，算法内部结构复杂，不适用于实时系统。Tian等［12］提出了一种基于测试人员性别、身高以及步频的步长计算模型，可以结合多种状态信息，但是该步长模型仅在行人步速或步频较高的情况下表现良好，当运动状态改变后精度下降。Ho等［13］提出了一种根据行人行走速度以及加速度变化特征动态调整的步长估计模型，但是模型中传感器数据来源于单一节点，而单个节点的数据无法包含全部的运动信息。Allseits等［14］将角速度传感器布置在行人的左右大腿、小腿4个位置，通过角速度变化信息检测行人步态并结合行人双腿长度信息计算前进速度，最终计算行人步长。但计算的结果会受到传感器绑定位置的影响，且同样存在仅依靠单一步态参数，未能结合其他数据信息的缺点。

针对以上问题，对Allseits等提出的方法在步态检测及步长计算部分进行改进，利用足部Z轴加速度与X轴角速度检测行人的步态信息，并通过腿部角速度的变化特征，对足跟着地动作的判定进行时域上的约束，最终根据测试人员的双腿长度信息、步态检测结果及腿部俯仰角信息计算行人的步长。

1 平走运动模型分析

本文结合人体下肢的结构特征，构建出七段刚体结构的运动模型，将行人平走运动过程描述为各刚体在三维空间的摆动行为。平走时行人下肢运动特征如图1所示。

图1 平走运动时行人下肢运动特征

图1显示的是一个完整的步态周期，包含足跟着地、足跟离地、脚掌着地、脚掌离地、空中摆动等几个重要的步态特征。

本文以足跟着地动作作为前一步态周期结束及下一步态周期开始的标志。将一个步态周期分为3个阶段：第1个阶段表现为行人的摆动腿整体向后弯曲并在空中达到最大弯曲程度，在这一阶段中，摆动腿的大腿会向前小幅度伸展，同时足部后蹬，小腿向后摆动；第2个阶段表现为摆动腿整体向前伸展并在空中摆动到正向的最大幅度；第3个阶段表现为摆动腿整体小幅度向后收缩，然后足跟着地，在这一阶段内，摆动腿的小腿与足部的摆动速度比大腿的摆动速度快，摆动幅度比大腿的摆动幅度大，当前步态周期结束后，摆动腿变为支撑腿，支撑腿变为摆动腿，开始下一步态周期。

2 硬件平台搭建

在第1节运动模型分析的基础上，本文设计了多节点实验平台，对行走中下肢各部位的运动情况进行跟踪，并提供相关的运动参数用于步态分析与步长计算。本文将IMU固定在人体的左大腿、右大腿、左小腿、右小腿、左脚、右脚6个位置。IMU的坐标系定义与固定方式如图2所示。

图2 多节点平台部署示意图

多节点平台由数据采集模块、数据处理模块、上位机等3部分组成。其中数据采集模块负责运动过程中身体各部位运动参数的采集，并完成原始数据预处理与相关校准工作，最终将解算后的姿态信息与传感器数据传输至数据处理模块；数据处理模块将各个节点采集到的信息收集整理，通过分析检测行人步态、计算行人步长，将结果以无线的方式传输到上位机；上位机负责最终的显示功能。硬件平台框图如图3所示。

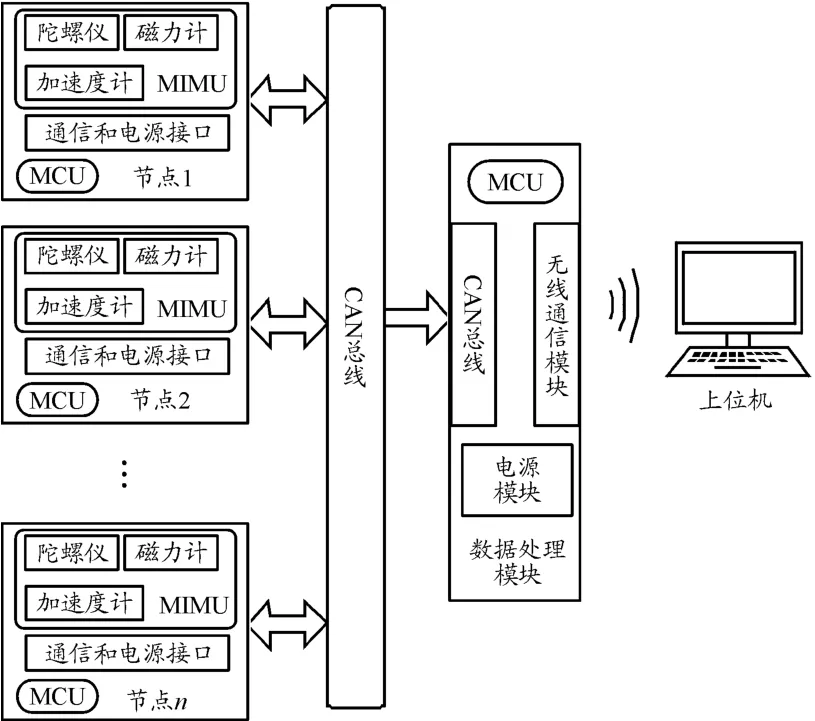
图3 硬件平台框图

3 步长估计算法

3.1 算法原理

在一个步态周期内，当行人一只脚足跟着地时，另一只脚的足跟会同时抬起，此时双腿处于支撑阶段。读取该时刻佩戴于两腿上4个节点的俯仰角信息，利用角度信息以及行人下肢长度信息即可完成步长的计算。将行人的下肢姿态描述为一个几何模型，如图4所示。

图4 平走步长计算模型

图4中行人的右大腿、左大腿、右小腿及左小腿的长度分别为L1、L2、L3、L4，而相应的俯仰角为θ1、θ2、θ3、θ4。通过分析可得，平走时行人步长的计算公式为：

通过以上分析，只要检测到足跟着地时刻，便可准确计算出行人的步长。因此，如何准确地检测出每个步态周期内足跟着地时刻是准确计算行人步长的关键。

3.2 步态检测算法

3.2.1 平走过程中节点数据特征

本文使用gx、gy、gz分别代表三轴加速度信息，ωx、ωy、ωz分别代表三轴角速度信息，θ、γ、ψ分别代表俯仰角、横滚角、航向角。并定义合加速度为Anorm，合加速度的计算公式为：

为了有效地检测每一种惯性数据在时域上的变化特征，并精确地捕捉到该数据在时域上的波峰与波谷，本文将窗口长度设置为5，定义如下的波峰、波谷检测方法。

式中：k代表被检测的惯性数据；ki-2、ki-1、ki、ki+1、ki+2分别是该惯性数据连续5个时刻的测量值。当pk＝1时，表示检测到该惯性数据的波峰，当vk＝1时，表示检测到该惯性数据的波谷。

本文首先采集了平走过程中足部节点的加速度与角速度信息，通过分析合加速度Anorm、Z轴加速度gz、X轴角速度ωx及俯仰角θ的变化特征，发现Z轴加速度gz和X轴角速度ωx的变化规律与实际的步态周期吻合度较高，可以应用于行人步态的检测。图5表示平走过程中足部Z轴加速度gz、X轴角速度 ωx、合加速度Anorm、俯仰角 θ的变化特征。其中，合加速度Anorm和Z轴加速度gz均为重力补偿后的值。

图5 行人平走运动足部节点运动特征

与实际运动情况对比可知，X轴角速度ωx的第1个波谷是由摆动腿足部后蹬动作引起的；波峰是由摆动腿足部前踢动作引起的；第2个波谷是由步态周期中第3个阶段内的动作造成的，包含摆动腿整体向后小幅收回、足跟着地2个重要行为。在陀螺X轴角速度ωx的波峰与第2个波谷发生的时间范围内，Z轴加速度gz会先出现一个峰值（代表足部前踢），然后出现一个波谷（代表足部回收与足跟着地这2个行为），其中波谷出现最小值的时刻为足跟着地时刻。

经分析可得，通过检测到足部节点的X轴角速度ωx的波峰后，再依次观察到Z轴加速度gz的波峰、X轴角速度ωx的波谷以及Z轴加速度gz的波谷的时域特征时，可对平走过程中的足跟着地动作进行检测。判断方法如下：

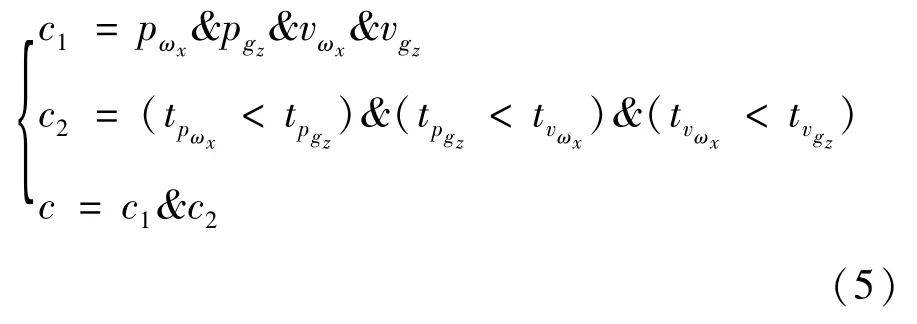
式中：tpωx、tpgz、tvωx、tvgz分别为 ωx波峰发生时刻、gz波峰发生时刻、ωx波谷发生时刻、gz波谷发生时刻；当c＝1时，说明成功检测出足跟着地动作，否则检测失败。

但平走过程中，足部的运动较为剧烈，使得足部节点的传感器输出波形会产生很多伪波峰和伪波谷，易造成峰谷的误判，影响对足跟着地动作的判别。与足部相比，腿部的运动平稳，且在行走过程中，行人两腿周期性交替运动，腿部节点的数据也呈现周期性的变化，传感器数据更加稳定。

为解决因足部剧烈运动造成伪波峰和伪波谷使得行人步态检测准确度下降的问题，本文通过在行人腿部安装传感器获得腿部运动信息，并结合足部数据进行分析，以提高步态检测的准确度。

图6表示平走过程中大腿、小腿X轴角速度ωx，足部Z轴加速度gz、X轴角速度ωx的数据变化特征。其中，为了方便观察变化规律，对Z轴加速度gz进行了一定比例的放大。

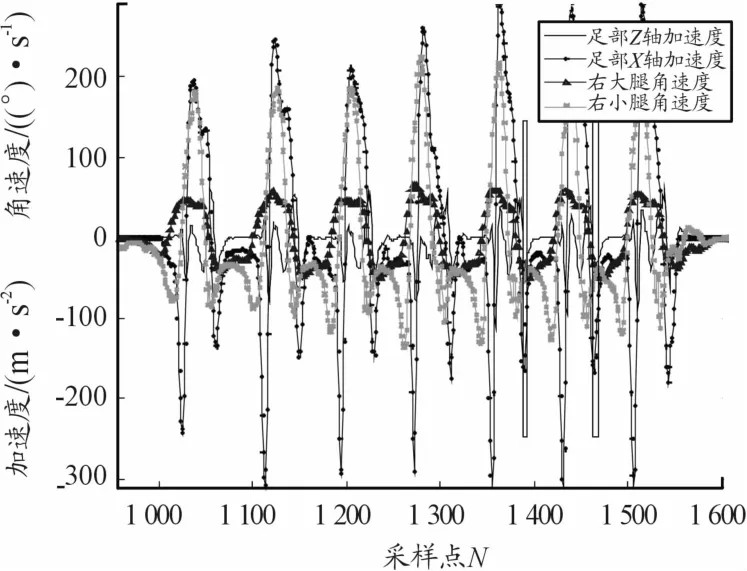
图6 行人平走运动腿部及足部节点运动特征

每个步态周期内，行人大腿、小腿上节点输出的角速度ωx都会出现明显的变化特征，均包含1个波峰、2个波谷。与实际运动情况对比可知，大腿、小腿角速度ωx的波峰均处于摆动腿的空中摆动阶段即步态周期的第2阶段；小腿角速度ωx的第1个波谷出现时刻晚于大腿角速度ωx的波谷出现时刻，且小腿角速度ωx处于波谷的时间范围内，大腿角速度ωx向波峰方向变化的时域特征符合步态周期中第1阶段内的腿部运动行为；小腿角速度ωx的第2个波谷处于步态周期的第3阶段，大腿角速度ωx的第2个波谷包含摆动腿整体向后收回，足跟着地及之后因重心变换身体整体前移，摆动腿过渡到支撑腿3个重要步态信息。因此，在这一阶段内，小腿角速度ωx波谷值到达时刻与足跟着地时刻会领先于大腿角速度ωx的波谷值到达时刻。图6中，方框内标记的是足跟着地时刻，晚于小腿角速度ωx的波谷值出现时刻，早于大腿角速度ωx的波谷值出现时刻。

通过检测小腿角速度ωx的波谷值出现时刻与大腿角速度ωx的波谷值出现时刻，可以进一步在时域上对足跟着地动作的捕捉进行约束。判断方法为：

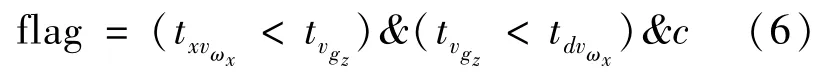
式中：txvωx为小腿角速度波谷出现时刻；tdvωx为大腿角速度波谷出现时刻；当flag＝1时，说明检测到正确的足跟着地时刻，否则检测失败。

3.2.2 算法模型设计

基于上述分析，本文设计了一种多条件约束步态检测算法，通过寻找足部节点X轴角速度ωx的波峰、波谷，Z轴加速度gz的波峰、波谷初步确定足跟着地的动作，并通过大腿、小腿节点的X轴角速度ωx的变化特征，在时域上对足跟着地时间点的确定进行进一步约束。算法流程如图7所示。

图7 步态检测算法流程框图

3.2.3 步态检测结果

利用多条件约束步态检测算法，可以准确地检测出一个步态周期内足跟着地时刻。图8为平走过程中，腿部俯仰角θ的变化特征以及步态检测结果。

根据本文定义的坐标系并结合实际运动情况，行人抬腿时，俯仰角会正向变化，达到正向最大值后略有减小，然后足跟着地。与此同时，另一条腿会向后弯曲，导致俯仰角负向变化。俯仰角的波峰值、波谷值出现时刻均处于一个步态周期内的第2阶段，即摆动腿的空中摆动阶段。从图8中可以看到，本文提出的多条件步态检测算法可以准确地检测行人的足跟着地动作。

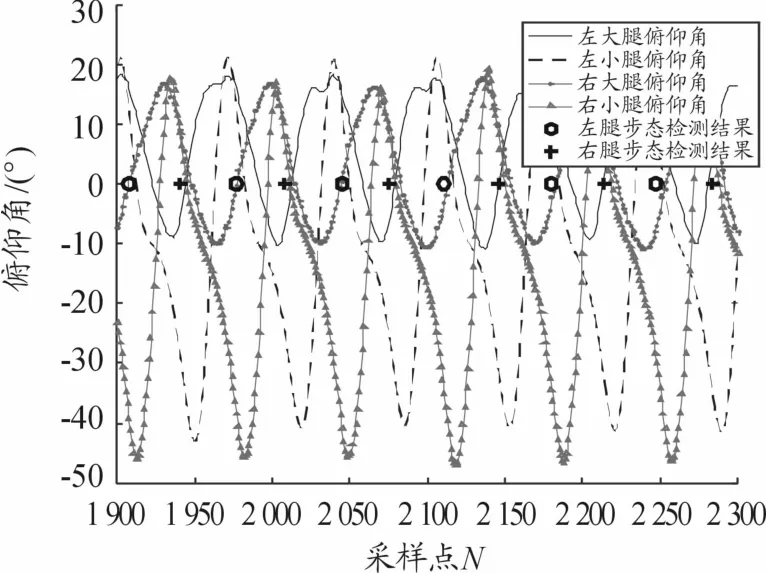
图8 行人平走运动腿部各节点俯仰角变化与步态检测结果

4 实验结果

为验证本文提出的分布式多节点行人平走步长估计算法的有效性，设计实验进行证明。实验采集了5名实验人员在长为60 m的水平路面往返行走过程中各节点的传感器数据，总共10组。利用多节点平走步长估计算法对行人步长进行计算，并与Weinberg等提出的单节点步长估计算法的计算结果进行比较。单节点步长估计算法的函数表达式为：

式（7）中：step_length为单节点步长估计算法每一步估计的步长；Amax和Amin为每一步中合加速度Anorm的最大值与最小值；K是模型的校准系数，设置为经验值0.5。

测试人员信息与多节点平走步长估计算法的计算结果如表1所示。2种步长估计算法的结果对比如表2所示。

为便于观察分析，将一组行人实际步长、多节点步长模型计算结果与单节点步长模型计算结果进行对比，如图9所示。

表1 多节点平台下的平走步长计算结果

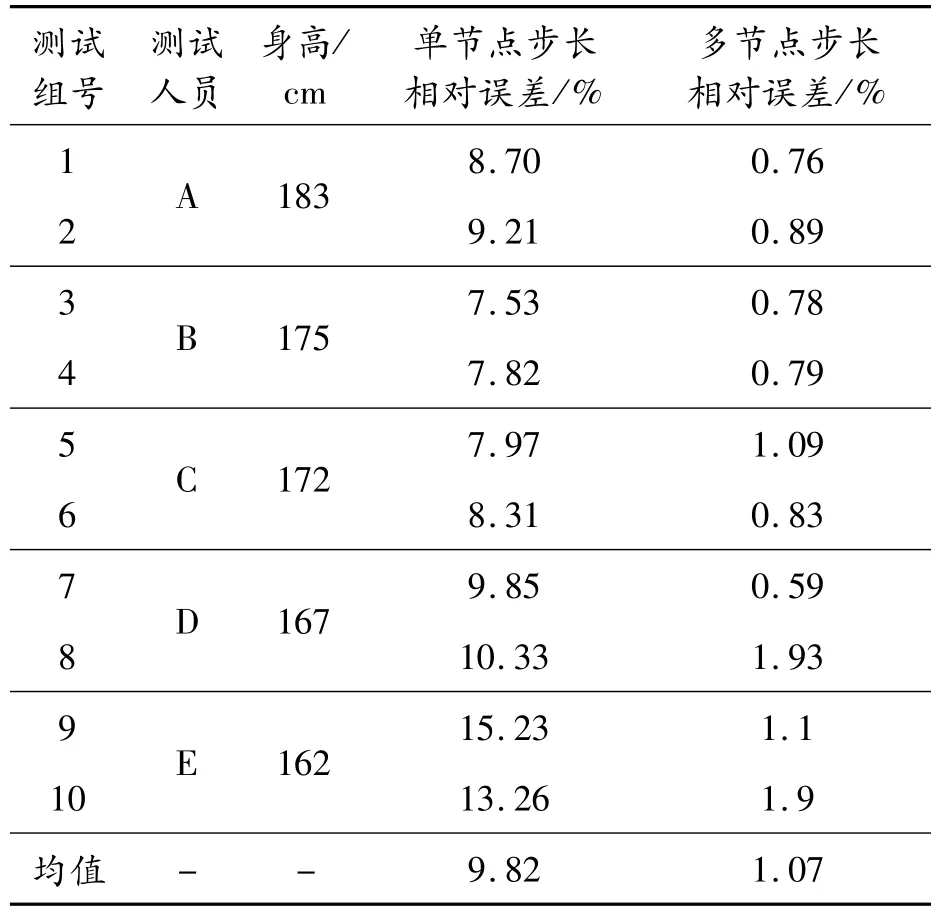
表2 多节点与单节点行人步长计算结果的比较

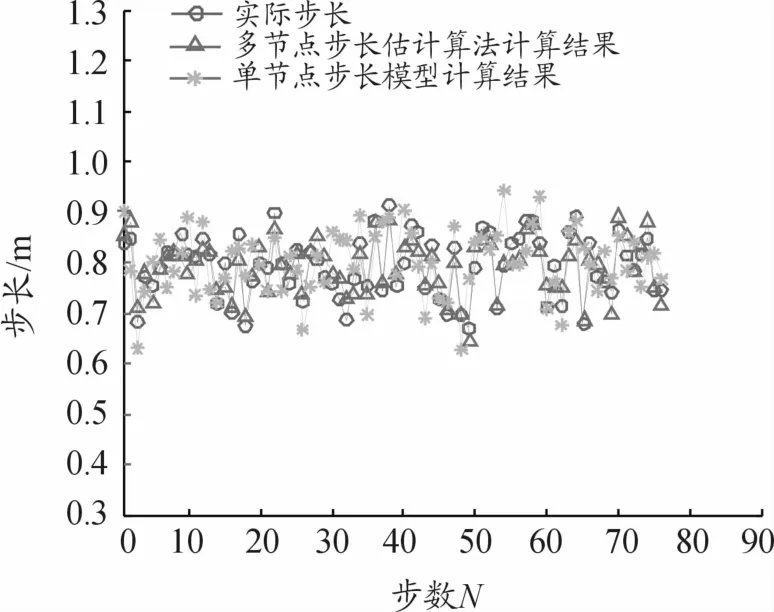
图9 步长计算结果对比图

从表1与表2分析得到，单节点步长估计模型计算的步长相对误差均值为9.82%；基于多节点平台的行人步长估计算法，其步长相对误差均值为1.07%；误差下降约为一个量级。从图9可以看出，多节点步长估计模型相比单节点步长估计模型的计算结果更加接近行人实际步长。

5 结论

针对行人惯性定位算法中步长计算精度较低的问题，提出了基于多节点运动姿态信息融合的行人步长自主估计算法。通过融合分析行人平走过程中足部节点与腿部节点不同位置的数据特征，对行人的步态、步长进行检测、计算，步长平均估计精度达到98.9%，平均误差相比传统步长估计算法下降约一个量级。算法具有原理简单、参数直观、实时性好、精度高、可结合身体各部位运动信息的优点，具有很好的工程应用前景。