徐盐高速铁路新洋港斜拉桥施工控制研究

李方柯 邹孔庆 王冰

（1.中铁第五勘察设计院集团有限公司，北京 102600；2.中铁四局集团钢结构建筑有限公司，合肥 230022）

1 工程概况

新洋港斜拉桥位于盐城市亭湖区通榆河和新洋港交口位置，设计采用（72+96+312+96+72）m 双塔双索面连续钢桁斜拉桥，是徐州至盐城高速铁路的全线控制性工程［1］。结构采用带纵向阻尼约束的半漂浮体系；主梁采用双主桁、三角形桁式，节间距12 m，桁高14 m，主桁中心距15 m，主桁采用焊接整体节点形式，杆件与节点之间采用高强度螺栓连接；桥面系采用正交异性钢桥面；桥塔采用129 m 高的花瓶形结构，单塔每侧设12对拉索。大桥立面布置如图1所示。

图1 大桥立面布置（单位：m）

新洋港斜拉桥的基础和桥塔采用常规方法施工，钢桁梁采用散拼法施工。为保证施工过程中结构的抗风稳定性，采用支架单向悬拼的方案（图2），先在承重支架上安装边跨和次边跨钢梁，再利用2 台70 t 全回转架梁吊机单向悬拼架设主跨钢梁，并挂设斜拉索，主梁在中跨跨中实现强制合龙［2］。

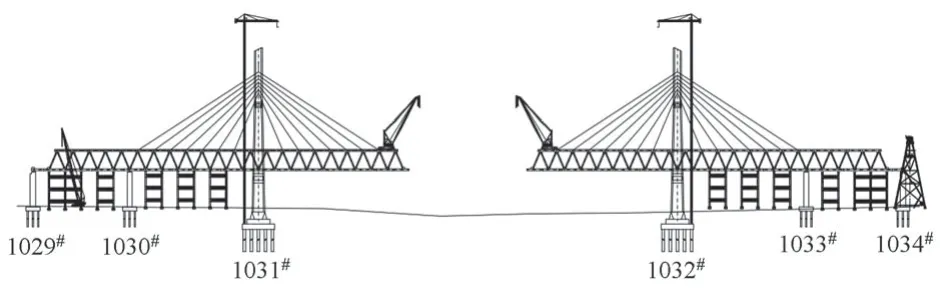
图2 支架单向悬拼法架设

2 施工控制概述

2.1 施工控制原则

斜拉桥施工控制的根本目的是对结构实际状态和理想状态的差异进行判别和修正，从而保证施工过程安全可控，使成桥结构线形和内力状态逼近设计理想状态。铁路钢桁梁斜拉桥的二期恒载和活载占比较大，施工过程中主梁内力通常不控制设计，主要通过控制线形以保证主梁顺利合龙。高速列车通行对桥面平顺度要求较高，在成桥状态控制主梁线形以满足列车通行需求更为重要。因此，有别于传统斜拉桥“线形内力双控”理念，铁路钢桁梁斜拉桥的施工控制宜采用线形控制为主、内力控制为辅的原则。

2.2 施工控制方法

斜拉桥施工控制以自适应控制法为主［3］，通过参数修正使理论计算模型更接近结构实际情况，从而对结构的真实状态进行判断和控制。

斜拉桥施工控制的核心在于处理结构实际状态与理论状态的偏差。产生偏差的原因包括：结构实际参数和设计参数存在差异、计算模型简化导致的结构力学行为和实际情况不一致、结构制造和安装误差、施工监测误差等。

新洋港斜拉桥采用自适应控制法消除参数误差，钢桁梁采用几何控制法［4-5］降低监测误差。但栓接钢桁梁的线形在杆件制造完成后已基本确定，后期安装标高调整量很小，钢梁的制造和拼装误差、仿真分析误差等造成的钢梁线形偏差只能通过斜拉索索力来调整。由于钢桁梁斜拉桥的索力线形敏感度相对较低，为保证钢梁线形，斜拉索索力可能出现较大的偏差。因此，新洋港斜拉桥施工控制在基于自适应控制的基础上，采用“线形精确控制+索力近似控制”的方法。

2.3 施工监控监测手段

新洋港斜拉桥施工监控计算基于无应力状态法［6-7］，采用三维空间有限元分析软件MIDAS 和TDV进行监控计算。桥塔、钢桁梁杆件等结构采用梁单元模拟，铁路正交异性钢桥面板采用板单元模拟，斜拉索采用索单元模拟，全桥按实际施工过程考虑几何非线性进行分析。

桥塔采用预埋式应变计进行应力、温度监测，塔柱采用棱镜进行位移监测；钢桁梁采用外贴式应变计进行应力和温度监测，采用全站仪和电子水准仪进行线形监测；斜拉索采用频谱式索力计监测索力。应变计采用自动化数据采集与分析。

3 重难点及解决措施

3.1 结构制造及安装线形

根据成桥线形、受力状态确定合理的结构制造及安装线形是斜拉桥施工控制的前提。传统方法一般根据施工阶段模拟计算确定从制造到成桥过程中结构的几何变位，然后采取各种方式加以几何补偿。目前，大跨度斜拉桥多采用无应力状态法确定构件的制造和安装线形，即根据成桥状态确定构件的无应力长度、无应力曲率、相对几何关系等参数，再辅以施工过程控制，最后达到预定的成桥状态。传统方法原理清晰、操作简便，对于大跨度桥梁则会出现较大的误差。控制构件的制造尺寸和几何关系对于超大跨度斜拉桥适应性较好，但过程繁琐，特别是几何控制量和制造、安装精度相近时则难以控制。因此，对于实际结构应综合几何控制参数、施工便利性等条件确定合理的线形控制方案。

新洋港斜拉桥钢梁按水平设计，各跨按1/2 静活载挠度设置预拱度，并通过桥面道砟进行竖曲线拟合，最终形成0.44‰的人字坡（图3）。主跨设143 mm预拱度，其中92 mm 通过调整上弦节点间距实现，51 mm通过张拉斜拉索实现。

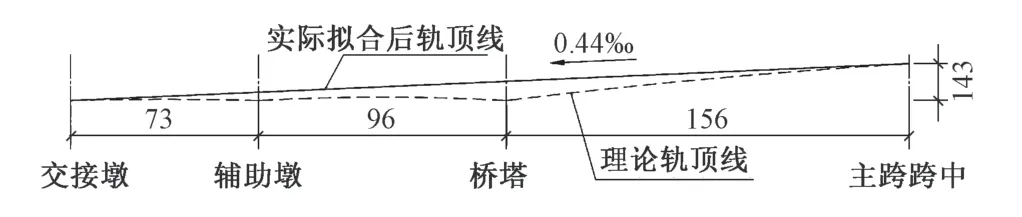
图3 钢梁成桥线形布置（单位：m）

根据监控结果计算得到钢梁梁端压缩量约为50 mm，各杆件的无应力长度比设计长度仅多出1～3 mm，与杆件制造误差在同一量级，控制几何尺寸较为困难。按无应力长度和杆件间无应力几何关系控制时，杆件拼接、腹板倾角、平联及横联角度均有较小的调整，不仅增加了制造复杂度，还会影响后期线形控制的判断。因此，该桥梁制造线形采用按设计长度制造+局部几何补偿的方法比较合理。因桥塔处设置了钢梁纵向顶推装置，钢梁选用强制合龙方案；考虑到梁端压缩值相对较小，钢梁最终采用梁端补偿的方案。

新洋港斜拉桥桥塔采用花瓶形混凝土塔，采用爬模分段现浇施工。桥塔线形控制按2 阶段计算、一次性补偿考虑。第1 阶段：计算桥塔施工阶段自重和收缩徐变引起的竖向变形、横向变形。第2阶段：计算斜拉索张拉和后期收缩徐变引起的竖向变形、横向变形。叠加2 阶段桥塔变形作为塔柱初始施工的预偏值，同时考虑桥塔上垫石以及斜拉索锚点的预抬量。斜拉索直接按照无应力状态法进行加工和控制。

综上所述，该桥施工控制最终采用无应力状态法+几何补偿法的方式来确定结构构件的制造和安装线形。线形监测结果表明，采用该方法成桥后梁、塔线形与理论线形吻合良好，各项线形误差均小于规范限值。

3.2 钢梁悬拼线形控制

新洋港斜拉桥钢梁采用单悬臂拼装，钢梁悬拼线形控制总体采用自适应控制原理，根据钢梁架设过程中的实际线形对计算模型进行不断修正，但模型修正无法消除计算模型简化误差和钢梁制造安装误差。新洋港斜拉桥钢梁前6 个节段的模型修正结果显示，仅调整主梁自重和斜拉索弹性模量2项对钢梁线形最敏感的参数，钢梁的理论线形和实际线形难以吻合。

考虑钢梁悬拼的首要目的是保证线形，实现合龙，所以允许斜拉索索力出现一定偏差。针对本桥提出了模型修正和索力调整相结合的控制方式：①对钢梁拼装施工过程进行计算，分析各斜拉索张拉对当前阶段梁端位移及合龙口位移的影响，引入索力敏感性参数β；②根据前3个悬拼节段线形修正计算模型关键参数，此时钢梁制造误差和拼装累积误差较小，模型修正效果较好；③在其后的3个悬拼节段施工过程中，根据索力敏感性分析结果调整索力，保证实际线形和理论线形一致。同时根据实际索力和钢梁变形对索力敏感性参数β进行修正。④此后每拼装3 个钢梁节段，对索力敏感性参数β再进行一次修正。

按照上述步骤建立钢梁悬拼线形与索力控制数据系统，对钢梁悬拼过程实时控制。实际施工情况表明，钢梁合龙前梁端高程和理论值差值小于5 mm，现场仅通过小幅调整中跨尾索就能实现钢梁合龙。

3.3 斜拉索初张拉拔出量

斜拉索的拔出量指索力在一定变化范围内，斜拉索的张拉伸长值（张拉端的拔出量）。斜拉索的拔出量主要有以下特点：①斜拉索在自重作用下会产生一定的垂度，索力增大时斜拉索的拔出量包括弹性伸长量以及克服垂度导致的伸长量；②由于斜拉桥为柔性体系结构，在斜拉索张拉过程中，塔端和梁端的锚点会产生一定的位移，影响斜拉索的拔出量；③斜拉索在自然状态下会产生一定的弯曲的扭转，在索力相对较小的区段内，索力变化值和索长变化值呈现强烈的非线性关系。因此，斜拉索的拔出量不仅与索的自重、弹性模量等参数有关，还与索力、索长、索的垂度、结构体系刚度等密切相关。分析和控制拉索的拔出量不仅是对其物理参数的校核，也可对结构的刚度进行验证。

分析索拔出量理论值时，初始索长通常按斜拉索在无自重作用下自由安装时的索长考虑（即无应力索长），即斜拉索安装前梁、塔端锚点的直线距离（图4（a））；最终索长按拉索张拉完成状态计算（图4（b）），此时斜拉索承受自重和张拉力F，塔端、梁端锚固点分别产生竖向变位ω1，ω2和水平变位υ1，υ2。索的理论拔出量=斜拉索的最终无应力索长-初始索长。

斜拉索张拉拉过程（图5）包括：①机动位移阶段。该阶段张拉力保持不变，索在张拉力作用下产生刚体位移，索的支承状态逐步由多点弹性支承转变为锚点支承；②垂度抵抗阶段。该阶段张拉力逐渐增大，索的拔出量不断增加，拔出量中以抵抗垂度产生的变形量为主；③弹性伸长阶段。该阶段张拉力进一步增大，索的拔出量不断增加，拔出量中以索的弹性伸长量为主。

图5 斜拉索实际张拉阶段

从斜拉索的实际张拉过程可以看到，其理想的初始状态（图4（a））并不存在，只有当张拉力达到一定程度时，其实际状态才与理想状态相对应。理论上应先根据锚固点坐标确定拉索的初始无应力索长，对斜拉索提前标记，待张拉完成后再次标记，将2次标记点的差值作为实测拔出量。由于实际的索锚点几何位置与理论存在偏差，且斜拉索制造先于锚点成型，斜拉索的初始标记可能存在较大误差，因此实际施工时一般不采用该方法。

基于斜拉索的实际张拉阶段和工作特性，提出2种方法对斜拉索拔出量的实测值和理论值进行对比：①零点弹性伸长对比。以斜拉索自由安装（计自重）变形后的索端拉力作为零点索力，以零点索力作为拉索张拉的垂度抵抗阶段和弹性伸长阶段的界限，假定后期拉索伸长量均为弹性伸长量。拉索拔出量校核仅考虑零点索力至初张力范围。②等效弹性伸长对比。考虑索力相对较大时，斜拉索基本已克服了垂度变形和弯曲扭转变形，其伸长量基本为弹性伸长量。斜拉索拔出量实测值采用张拉后几级的伸长量作等效替换，并与理论值进行对比。

以新洋港斜拉桥北岸侧1031#桥塔1～4 号索为例，按上述2 种方法对拉索拔出量进行验证，见表1。其中，S1′为边跨1 号索，S1 为中跨1 号索，-1 为东侧索，-2 为西侧索。实际拉索按初张力分5 级张拉，第1级直接张拉至理论零点索力，等效弹性伸长对比时采用后3 级伸长量等效替换得到的实际拔出量。由表1可知，斜拉索实际拔出量和理论值误差均在6%以内，验证了斜拉索弹性模量和理论值相符，结构整体刚度与理论值接近。表明按照零点索力法或等效弹性法进行斜拉索初张拉拔出量校核可靠。

3.4 二次调索

对于铁路钢桁梁斜拉桥，二次调索的目的是保证钢梁线形和设计线形尽量一致，并使斜拉索索力接近设计值。一般采用调整拉索拔出量的方法进行二次调索。由于斜拉索的实际长度与结构实际刚度、施工误差、温度、张拉力等诸多因素相关，因此采用相对调整法进行二次调索。

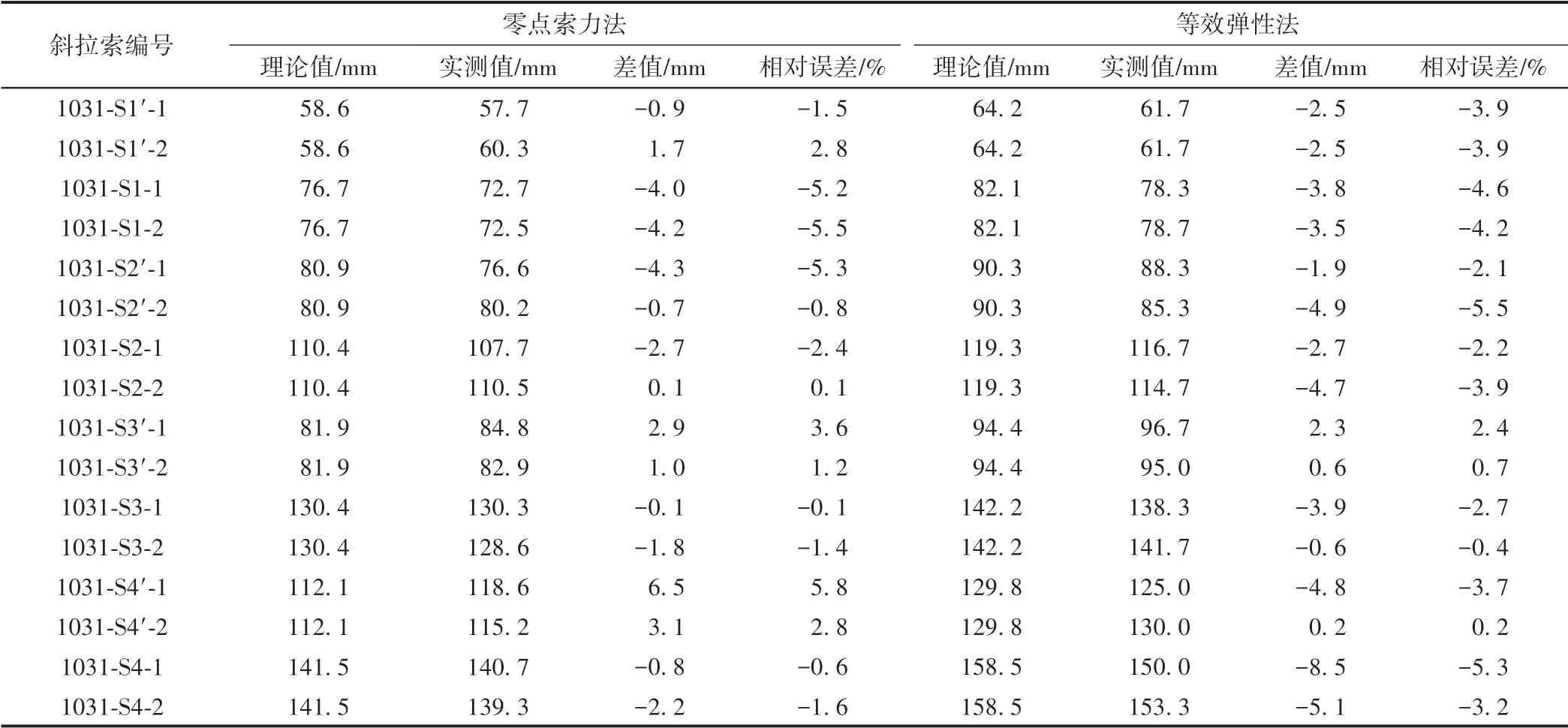
表1 斜拉索初张拉拔出量对比

按照二次调索前后的计算模型即可确定斜拉索拔出量。斜拉索在调索前后的状态如图6 所示。其中，A，B，C，D 为锚固点，DE 段为张拉拔出段，调索前后索力分别为F1，F2。令AB 段、CD 段、DE 段的无应力长度分别为L1，L2，L0，DE 段实际长度为ΔL。考虑温度T，线膨胀系数α，斜拉索的弹性模量E和面积A。根据无应力长度不变原则，忽略DE 段垂度影响可以得到ΔL=（L1-L2）［1+F2/（EA）+αT］。

图6 斜拉索张拉前后状态

根据斜拉索实际工作参数F2=5000 kN，T=30 ℃，E=195 GPa，A=13431 mm2，α=1.2×10-5计算得到F2/（EA）+αT=0.00226，该项可忽略。因此，二次调索拔出量计算公式可简化为ΔL=L1-L2。理论上仅需要计算出二次调索前后模型各斜拉索的无应力长度即可。

根据钢梁悬拼线形控制结果可知，钢梁合龙后其线形与理论线形基本相同，但索力实测值和理论值不符，且不成比例。为避免成桥后斜拉索索力出现较大偏差，应基于实际情况采用相对调整法进行二次调索。由于二次调索与索力绝对值无关，决定钢梁线形达到理想线形的指标是索力的变化量，即张拉拔出（Fn为第m根斜拉索的索力）和钢梁线形差方和量。因此，以斜拉索索力差方和2（Hn为第n个钢梁控制点的高程）最小作为控制指标，对调索前模型进行调整，使索力理论值接近实测值。结合调索前后模型即可确定各斜拉索的二次调索拔出量。

二次调索后钢梁东、西侧各控制点高程实测值和理论值的差值见图7，1031#墩斜拉索索力实测值和理论值见图8。可知，钢梁实际线形和理论线形吻合良好，高程误差基本在20 mm 以内；斜拉索索力实测值与理论值吻合较好，实际索力约为理论值的1.08 倍，差值主要由钢梁预拱方法以及制造和拼装误差引起。实测结果表明钢梁线形、斜拉索索力均满足设计要求。

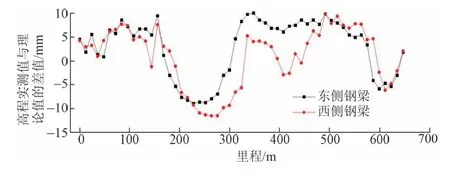
图7 钢梁高程实测值与理论值的差值

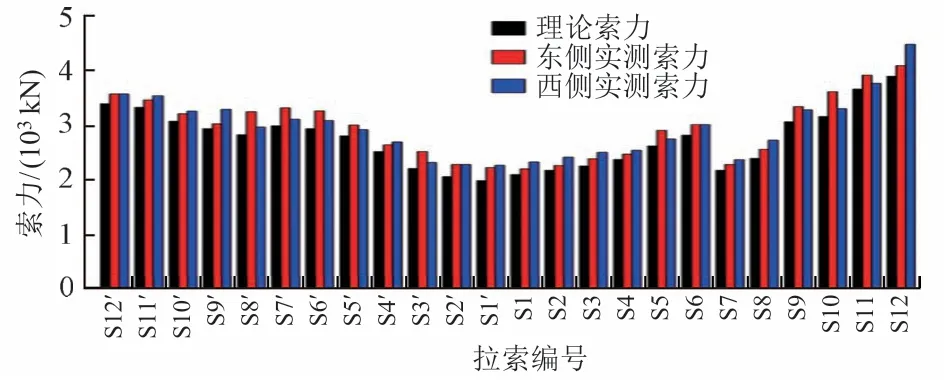
图8 1031#墩斜拉索索力实测值与理论值

4 设计优化建议

4.1 成桥线形

铁路斜拉桥在列车通行时将产生较大的竖向位移，应设置预拱度以保证线路的平顺性。传统方法是按照恒载+1/2 静活载的挠度曲线设置预拱度。铁路客车、货车设计荷载分别为64（ZK），85 kN/m（ZKH），而实际运营荷载仅为28，66 kN/m，且按传统方法设置预拱度会导致线路不平顺。因此，预拱度设置时应结合实际活载考虑。

对于钢桁梁斜拉桥的成桥线形，若按主梁水平设计在各跨分别设置预拱度，则预拱度曲线在支点处会出现不连续的情况，成桥后还需要对轨道线形进行拟合。该传统方法仅适用于有砟轨道。预拱度的设置受预拱方法、施工误差影响，控制困难。同时，钢梁成桥线形受温度影响较大，成桥后轨道线形拟合困难，易出现成桥轨道线形和设计轨道线形不一致的情况［8］。设计时可根据钢梁预拱度将线路局部调整为人字坡，钢梁直接按照实际人字坡线形进行设计和制造。

4.2 构造设计

除制造和拼装误差外，钢桁梁的拼装工艺和预拱度设置方法是影响钢梁线形控制的主要因素。钢桁梁的拼装工艺主要有焊接和栓接2 种，新洋港斜拉桥钢梁均采用栓接连接，施工时采用散拼的方式。由于杆件栓接拼装时可能绕节点转动，会造成拼装线形误差并逐步累积。因此，在施工条件允许的情况下，钢桁梁宜采用整节段先焊接后拼装或多节段先焊接后拼装的工艺，便于施工线形控制。

钢桁梁的预拱度成形方法主要有调整上弦节点间距尺寸、张拉斜拉索起拱、调整钢梁制造线形等。调整上弦节点间距尺寸是实现钢桁梁预拱的传统方法，但调整尺寸一般较小，钢桁梁的节点刚域难以准确考虑［9-10］，线形控制困难。张拉斜拉索起拱会增大索力，边跨压重也需增加，一般仅适用于对斜拉索刚度需求高且压重便利（或不需压重）的钢箱混合梁斜拉桥。调整钢梁制造线形的方法更有利于钢桁梁的线形控制。考虑钢梁的制造、拼装误差等，采用调整钢梁制造线形为主、张拉斜拉索起拱为辅的方案较为合理，且钢桁梁边跨压重应具备足够的富裕度。

从钢梁线形的敏感性分析来看，钢梁自重是主要影响因素，斜拉索刚度是次要影响因素。对于钢桁梁斜拉桥，索力变化对钢梁线形的敏感度相对较低，当自重、二期恒载出现偏差或制造、拼装误差导致钢梁实际线形和设计不一致时，需要调整的索力较大。因此，钢桁梁斜拉桥设计时斜拉索宜留有足够的富裕度，以保证成桥后斜拉索的强度安全系数满足规范要求。

5 结论

1）基于自适应控制原理，采用“线形精确控制+索力近似控制”的原则。施工控制采用无应力状态法+几何补偿法的方式确定结构构件的制造和安装线形。钢梁悬拼线形采用线形精确控制+索力近似控制的方式，有效保证了钢梁合龙线形。

2）采用零点索力法或等效弹性法在斜拉索初张拉阶段实现了索力和拔出量双控，能够及时发现斜拉索及其相关设备的质量问题，是斜拉索施工控制的重要手段。

3）采用无应力状态法结合实际索力进行二次调索，在保证成桥线形的基础上，各斜拉索索力应尽可能逼近设计成桥索力。

4）对于铁路钢桁梁斜拉桥，设计预拱度宜结合实际活载设置，采用人字坡线路来拟合钢梁预拱度。预拱度设置宜采用调整钢梁制造线形为主、张拉斜拉索起拱为辅的方案。为保证成桥钢梁线形，设计时斜拉索宜留有足够的富裕度来消除各项误差。

新洋港斜拉桥于2016年3月开工建设，2018年8月钢桁梁顺利合龙，2019年12月正式通车运营。大桥实测线形、内力状态良好，达到了设计的理想状态。