坡屋面建模计算及配筋设计相关问题研究
刘孝国 李 欣 杨金强
(1.中国建筑科学研究院 北京构力科技有限公司,北京 100013; 2.山东东瑞规划建筑设计院有限公司,济南 250011)
引言
坡屋面因其形象美观、造型独特倍受建筑设计师的青睐,被广泛用于各种各样的建筑中,如体育馆看台、住宅屋顶造型等,但大部分结构设计师对于坡屋面的受力分析及配筋设计未形成完整、准确的认知。设计中对坡屋面的斜板按照投影的平板进行内力计算及配筋设计,对于结构整体指标(刚度比、周期比、位移比等)按照平板建模计算结果考察。整体建模计算及构件配筋设计中按照平屋面建模计算或坡屋面布置不正确导致斜板未参与整体分析,各种对坡屋面的简化模拟,会导致计算模型与实际工程存在较大出入,工程设计中造成安全隐患或不同程度的浪费。本文结合PKPM软件对于坡屋面的建模及计算处理原则,对设计人员坡屋面常用建模的几种方式做深入剖析,通过实际案例,解析坡屋面设计过程中的一系列重要问题,如与斜板相连梁的内力分析、配筋设计及结构整体各项指标等,并给出设计建议,供设计人员在设计此类工程时做参考[1-3]。
1 坡屋面的建模[4-6]
PKPM软件中坡屋面建模有以下几种方式:
1.1 仅有斜板的坡屋面楼板建模
采用调整上节点高的方式,形成坡屋面。在PMCAD中,将坡屋面屋脊处最高的高度设置为层高,坡屋面下的其他节点的上节点高设置为负值,这样程序通过搜索房间边界杆件,只需要将斜板周围的杆件端点的标高进行调整,通过斜梁或者斜坡墙围成房间,即可生成对应的楼板数据,自动形成坡屋面斜板[7]。
1.2 既有平板又有斜板的坡屋面楼板建模
如果存在坡屋面下层有平板,上层有坡屋面斜板,为保证坡屋面上荷载的正确传递,必须在坡屋面下檐布置一道封口梁。坡屋面外沿的封口梁和其下层楼面的封口梁处于同一位置,是重合的,他们同时连接下层楼板和坡屋面的斜板,并同时承担两层楼板传递来的荷载。在输入这种坡屋面结构的封口梁时,可在下层输入实际尺寸的梁,在坡屋面层输入截面尺寸为100*100的虚梁。坡屋面封口梁的作用是为了生成坡屋面的屋面板,同时进行楼板导荷,程序在计算时自动将仅保留一根梁,自动将上层虚梁的荷载加到下层楼面梁上。
在PKPM软件V4.3版本中,这种平板和斜板共存的坡屋面也可通过自动形成一层斜坡屋面和布置一层层间楼板实现整体建模,如图1所示为采用层间板加坡屋面按一层建模形成的坡屋面效果。层间板程序自动按照弹性板考虑,进行网格剖分,考虑其对结构整体刚度的影响,楼板网格剖分情况如图2所示。

图1 按照层间板方式输入坡屋面下的平板

图2 坡屋面及其下的夹层平板网格剖分情况
1.3 有高低跨的坡屋面楼板建模
对于坡屋面高低跨的建模,可以按照不同标高的梁布置,修改梁两端标高建模,也可以按照不同的标准层建模,需要调整柱底标高。最佳的建模方式是采用层间斜梁方式,其不仅可以打断相应柱,不同高度坡屋面的荷载导算也能正确传递,而且可避免使用分层方案造成某些计算指标(如层间位移角等)可能不恰当的情况发生。
2 坡屋面建模中的特殊情况
2.1 斜坡屋面建模的共面问题
围成斜板的杆件必须共面,PKPM软件建模中要求板的节点高差在1m范围内的斜板都可以强制自动形成共面楼板,节点高差超过该高度的,该板计算时被扔掉,但是保证板上荷载不会丢失。如图3所示为布置的坡屋面斜板,建模中看到楼板好像是布置上去的,但在SATWE计算中这种板其实是被过滤掉,并没有参与分析。

图3 建模布置的不共面楼板三维显示图
通过分析模型下的“空间简图”看到网格剖分情况,如图4所示,图中标记出的那几块斜板没有网格剖分,就未参与分析,楼板丢掉。大量的坡屋面工程因为未遵循该楼板形成规则而造成斜板丢失,从而导致计算结果与真实情况产生较大出入,可能造成结构设计产生安全隐患。对于类似坡屋面等复杂情况,如果板周边构件确实无法共面建模,则可以考虑增加虚梁将斜板分成几块共面板,每一块由于虚梁划分都保证了四个节点共面,楼板才能参与后期的整体分析。

图4 SATWE空间简图下楼板网格剖分情况
2.2 按照斜杆输入斜梁形成坡屋面
PMCAD建模中,一个房间仅仅能生成一块对应的楼板。如果坡屋面满足上述共面条件,按照斜梁形成的封闭区间,程序可以自动生成坡屋面。如果坡屋面中的斜梁按照斜杆建模,需要注意斜杆是不参与房间的划分的,也就是说按照斜杆建模程序无法自动形成对应的斜板。因此,在进行坡屋面斜构件布置的时候,不建议按照斜杆布置斜梁,而应该按照斜梁布置,形成闭合房间让程序自动形成共面楼板。
3 坡屋面及其斜梁软件处理原则
3.1 程序对于封口梁的处理原则
SATWE程序对坡屋面斜梁与下层梁直接连接的情况,程序可以自动连接生成斜梁与下层梁直接的连接关系。程序对这种同一位置重合梁(封口梁)做荷载合并和删除机制,将他们作用到下层梁,然后将上层的梁在计算时删除,避免刚度重复计算。荷载合并和删除机制保证坡屋面封口梁结构的正确计算和设计。坡屋面的封口梁主要起导算荷载作用,其与下接楼层梁或墙之间的一一对应的关系,是建立坡屋面与下层构件之间正确连接连接关系的基础。
3.2 软件对于斜板荷载处理原则
坡屋面斜板上的房间恒、活荷载,软件将板上荷载导算至周边梁、墙等构件上时,按该斜板的水平投影面考虑。坡屋面荷载导算面积如图5所示。通过SATWE生成的分析模型中“错误定位”,查看到坡屋面的荷载导算情况,如图6所示。需要注意的是《建筑结构荷载规范》GB50009-2012(以下简称“荷载规范”)中对于活荷载是按照投影面计算的,因此,在软件中输入时,直接输入板面上的活荷载即可,不考虑斜板倾角角度问题。对于板自重程序可以自动计算,并考虑倾角,但如果要输入其他恒载,应该考虑楼板的角度,按照图5所示的关系考虑。

图6 “错误定位”中坡屋面导算在梁上的荷载图
3.3 程序对于斜板的刚度考虑
斜板的计算属性,SATWE和PMSAP软件均默认按弹性板考虑,设计师可以将其定义为弹性板6,但是不能定义为弹性板3,当然强制刚性楼板假定对斜板也不起作用,即使勾选“全楼刚性楼板假定”,程序对斜板仍然按照默认弹性膜或者自定义的弹性板6考虑。斜板(弹性模)的平面内刚度按照实际刚度考虑,其平面内刚度在程序计算中被分解为世界坐标系下X、Y两个方向的分量,X分量具有水平板的属性Y分量具有竖向墙的属性,弹性膜不考虑平面外刚度。
斜板与墙相连,由于板边界上具有与墙相同的公共节点,因此,剪力墙与斜板之间完全协调,对于斜板与斜梁的情况,目前程序内部默认梁板协调,板剖分的节点与梁位置对应的节点完全变形协调,梁板的共同作用通过中梁刚度放大系数来反映。
3.4 判断楼板是否参与整体分析
判断斜板不共面或者斜板是否丢失的办法。在建模中可通过三维方式直观查看斜板布置是否正确,但有些情况由于偏心、标高等原因,造成即使在PMCAD中正常显示的斜板,在计算模型中也可能会被判断为不共面情况而过滤掉。因此,最直接的方式是在SATWE计算分析模型中的“空间简图”查看斜板是否参与网格划分,如果网格剖分即该板参与计算。
3.5 PMSAP对于不共面楼板的特殊处理
上述图3所示的不共面楼板,在PMSAP中可以形成曲面进行处理,如图7所示,对于类似或者更加复杂的不共面楼板,PMSAP都可处理,使楼板参与整体内力分析。需要注意的是,如果楼板不共面很严重,此时虽然可以形成曲面,但应检查生成的模型是否符合实际情况,对结果做细致校核。
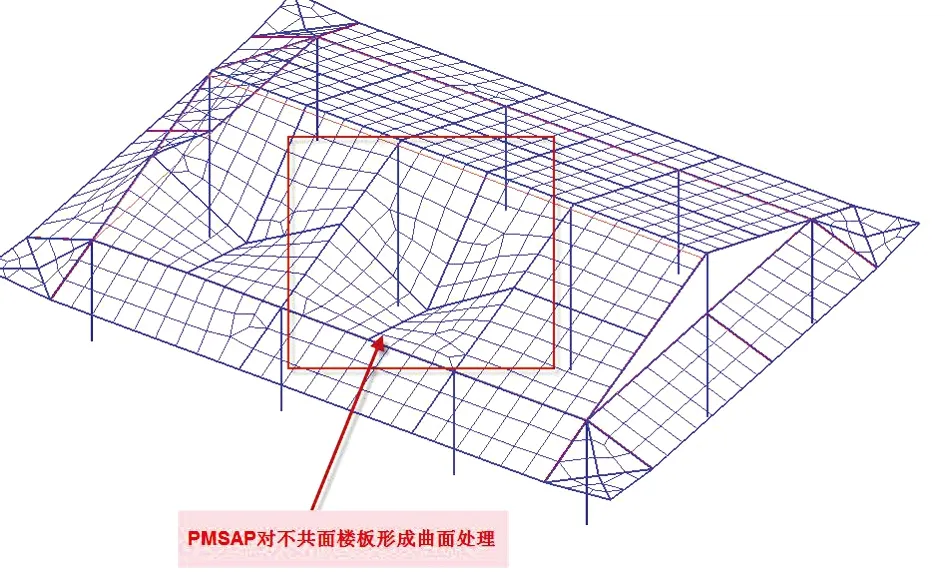
图7 PMSAP对不共面楼板的特殊处理
4 不同情况的算例工程
对坡屋面建模计算时,设计人员往往认为不考虑斜板设计一般偏于保守,或者按照平板去简单模拟,但实际上斜板对结构刚度、内力影响很大,不同的斜板坡度对结构的影响大小有别。下面以几个工程为例,使用SATWE软件分析斜板对整个结构刚度、内力及指标影响; 同时着重考察不同坡度下与斜坡屋面楼板相连梁的内力与配筋[8]。
4.1 不考虑斜板的模型1
该工程为钢筋混凝土框架结构,其中框架梁的截面300mm*600mm,中间榀重点研究位置梁截面600mm*1200mm,柱截面800mm*800mm,柱距8m,层高6m,斜坡屋面坡度10度,布置板厚为0,恒载8kN/m2,活载4kN/m2,7度0.15g,Ⅲ类场地土。模型1是无斜板的,即不考虑板作用的计算模型,如图8是模型1的三维图,图9是重点研究榀计算的恒载作用下的弯矩图。结构总质量1593.5t; 前三个周期分别为1.2491s,0.5077s,0.4401s; 底部剪力为:X向381.5kN,Y向1193.8kN。
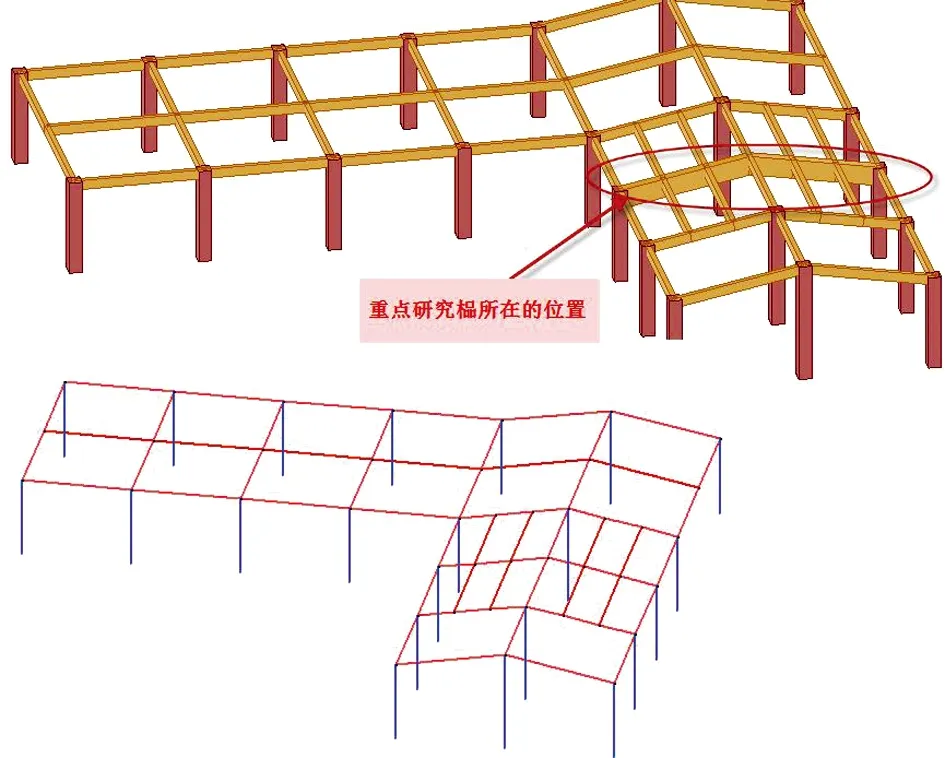
图8 模型1三维模型及计算简图

图9 模型1研究榀恒载下弯矩图(单位:kN.m)
4.2 考虑100厚斜板的模型2
模型2几何属性同模型1,荷载情况也一致,唯一不同是布置了100厚的斜板,并且不考虑板重。计算模型的“空间简图”如图10所示,可以看到斜板参与了网格剖分。该模型2计算的总质量1 593.5t; 前三个周期分别为0.3793s,0.3573s,0.3282s; 底部剪力为:X向1 868.1kN,Y向1 760.9kN。图11是所选取研究榀恒载作用下的弯矩图。
4.3 考虑100厚斜板角度20度的模型3
模型3几何属性不同模型2,相比模型2,斜板坡度从10度增加到20度,荷载情况一致。计算模型的“空间简图”如图12所示。模型3计算的总质量1 606.4t,前三个周期分别为0.3732s,0.3554s,0.3338s,底部剪力为:X向1 919.3kN,Y向1 906.8kN。图13是重点研究选取榀恒载作用下的弯矩图。

图11 模型2研究榀恒载下弯矩图(单位:kN.m)
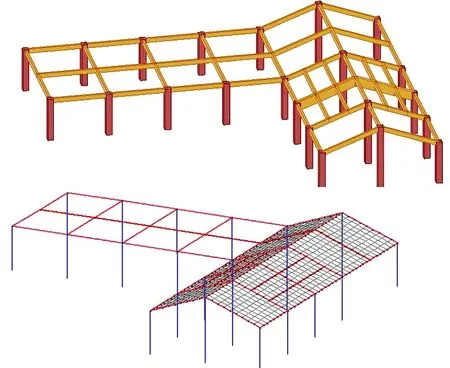
图12 模型3三维模型及计算简图网格划分图
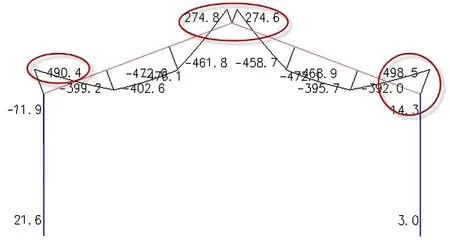
图13 模型3所选取榀恒载下弯矩图(单位:kN.m)
4.4 考虑100厚斜板角度60度的模型4
模型4几何属性不同模型3,相比模型3,斜板坡度为60度,荷载情况一致。计算模型空间简图如图14所示。模型4计算的总质量1 660.8t,结构前三个周期分别为0.4173s,0.3837s,0.3598s,底部剪力为X向3 744.9kN,Y向3 966.5kN。图15是所选取榀恒载作用下的弯矩图。

图14 模型4三维模型及计算简图网格划分图

图15 模型4选取榀恒载下的弯矩图(单位:kN.m)

图16 模型5三维模型及计算简图网格划分图
4.5 考虑100厚平板的模型5
模型5 属于100厚平板模型,荷载与前面的几个模型都一致。计算模型的空间简图如图16所示,计算的结构总质量1 579.8t,前三个周期分别为0.3713s,0.3397s,0.3092s,底部剪力为:X向1 734.9kN,Y向1 676.5kN。图17是所选取榀恒载作用下的弯矩图。

图17 模型5选取榀恒载下的弯矩图(单位:kN.m)
5 五个模型周期、内力结果对比分析
对上述五个模型结果进行比对,汇总如表1所示的对比结果,表中列出了对应五个模型的质量、周期、底部剪力及对应研究选取榀梁在恒载下的支座和跨中弯矩值。
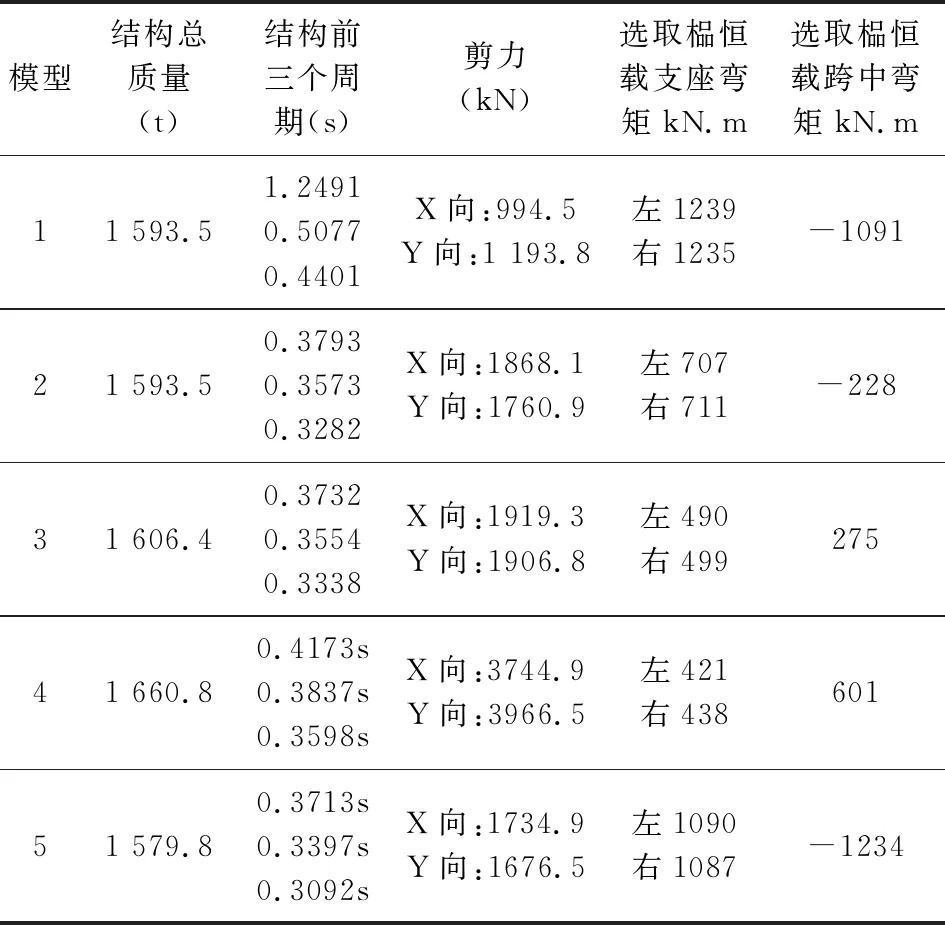
表1 模型1-模型5计算结果对比
5.1 有无斜板对结果的影响
表1中模型1与模型2的结果比较发现,斜板是否参与计算对于结构整体刚度影响很大,导致周期及底部剪力差异较大,最大的X方向剪力有无斜板大概差了1倍。对于选取的研究榀,无斜板的模型1中的斜梁表现出典型门式刚架梁的受力形式,支座弯矩与跨中弯矩都较大; 模型2中有斜板的梁,由于10度斜板的作用,在梁梁相交跨中部位产生了较大的相互支撑作用,使得弯矩值大大减小,变化幅度与模型1相比差4倍。梁支座部位的负弯矩也由于板的约束作用,由无楼板的1200kN.m变为有斜板的700kN.m,相差大概40%。模型1、2的对比很好的解释了很多设计师的一个疑问,按照不考虑斜板与考虑斜板相连的梁内力有时候差好几倍。
5.2 不同斜板坡度对结果的影响
模型2与模型3的周期结果对比发现,随着斜板的倾斜角度变大,结构整体刚度变大。从研究榀的梁的弯矩结果对比发现,斜板倾斜角度从10度变为20度,导致梁跨中弯矩反号,由-228kN.m变为275kN.m,即坡屋面坡度变大时,支承作用变强,产生了更强的约束,更具有了竖向墙的属性。研究榀梁的支座弯矩,由700kN.m变为500kN.m,支座弯矩减小幅度30%以上。从上述对斜梁结果的对比可知,如果不正确考虑楼板作用会导致梁跨中弯矩计算结果完全错误,本来受拉的结果可能会被判定为受压,会导致钢筋配置完全错误。
模型2、3再与模型4比较,较大倾斜角度下,楼板具有更大的竖向刚度,导致结构底部剪力较小倾斜角度楼板的剪力大了1倍,对底部剪力影响明显。由于斜板的约束作用变大,导致与斜板相连的观察榀斜梁的相交部位约束更强,梁端产生更大的负弯矩。
5.3 无楼板与平板的结果对比分析
模型1与模型5的计算结果对比发现,由于有平板的作用,导致结构整体刚度变大,地震作用下的底部剪力较没有楼板的大,最大X方向差距在45%左右。当然无楼板与平板相比,对于研究榀梁的弯矩影响比较小。
模型2与模型5的计算结果对比发现,平板和斜板作用下对应的结构的整体底部剪力差异并不是很大,但是对研究榀梁的支座和跨中的弯矩影响很大,跨中最大的影响弯矩差了大概5倍。
5.4 研究榀梁恒载轴力、柱恒载剪力对比
由于柱剪力一部分是由梁轴力引起的。表2列出了研究榀梁恒载下轴力、柱恒载下剪力的内力对比结果。

表2 研究榀梁恒载轴力、柱恒载下剪力
通过对比前4个模型,发现没有楼板的斜坡屋面对应的柱剪力是最大的。对于斜板的模型,斜板角度越大,对于柱产生的剪力越小; 梁的轴力随着坡屋面坡度的变大,跨中轴力减小,支座轴力变大。正常的平板结构,柱剪力是小于没有楼板的斜坡屋面所对应柱的剪力。斜板的参与影响了与之相连的框架柱的剪力,坡度越大,柱子的剪力越小。
5.5 研究榀梁地震作用下弯矩对比
表3列出了研究榀梁在X地震下模型1~模型4的梁端及跨中弯矩结果。

表3 研究榀梁在X地震下跨中及支座弯矩
模型1~模型4相比,结构底部总剪力,模型4的最大,模型2,3比较接近,模型1底部剪力最小。该研究榀的梁端弯矩,模型4是最大的,模型2与3的弯矩比较接近,模型1的弯矩是最小的,并且模型1的梁端弯矩结果与其他三个模型差异较大,与模型4相比差异1倍以上。四个模型X向地震作用下梁端弯矩变化趋势与结构底部剪力变化规趋势一致。斜板坡度越大,刚度越大,对应地震剪力越大,分配到对应的梁构件上的弯矩也是越大的。
6 五个模型梁、柱配筋结果对比
列出5个模型研究榀梁、柱的配筋结果如表4所示。
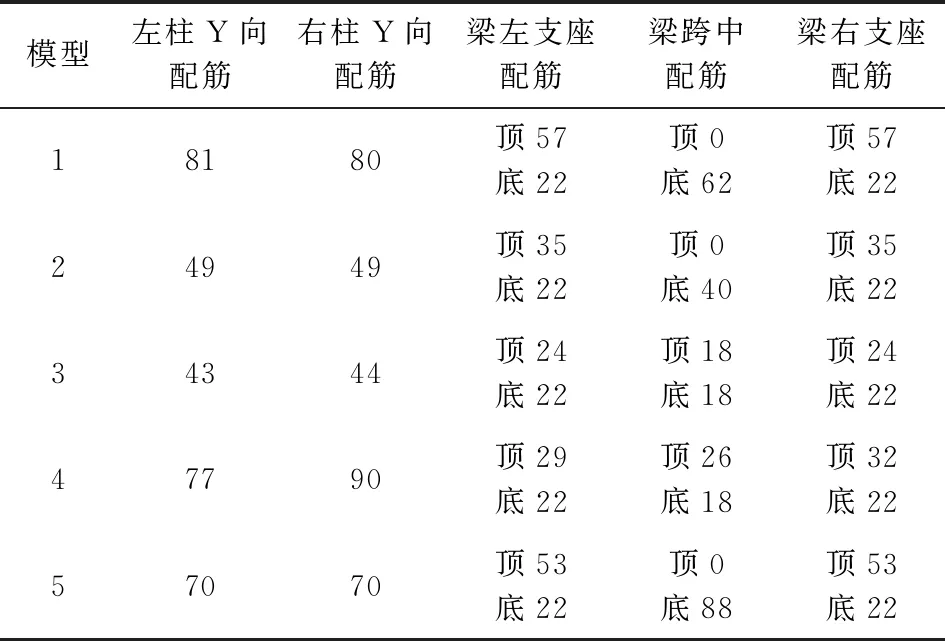
表4 研究榀梁、柱配筋结果
通过上述的对比发现配筋具有如下规律:
6.1 柱配筋结果对比
模型1的柱配筋大于模型5的配筋,即没有楼板参与的模型1柱配筋是最大的。有斜板的模型比较,柱配筋最大差异1倍多,柱配筋最大的是模型4,最小的是模型3,因为柱配筋控制考虑了地震作用,变化趋势不太有规律性。但是从以上的对比结果可以看到,计算中应该考虑楼板参与工作,并应真实模拟坡屋面的坡度,不同的坡度对柱配筋结果影响很大。
6.2 梁支座配筋结果对比
由模型1,2对比发现,有楼板参与导致研究榀梁梁相交部位约束变强,梁支座部位弯矩分布发生变化,梁端受拉钢筋面积有楼板时减小。模型2,3比较发现,随着斜板坡度变大,梁支座处配筋减小,主要是由于支座处的弯矩减小,梁梁相交部位约束变强。模型4与3比较,梁支座配筋反而增大,主要是模型4较模型3中梁恒载下轴力有大幅度的减小,此处的梁配筋已经变成了拉弯构件控制配筋。
模型1与5相比,有平板的梁支座配筋较无楼板配筋减小,主要原因是恒载作用下模型5的弯矩较模型1 的小,且模型5的梁是纯弯构件的配筋,而模型1中的梁属于斜梁,配筋是由拉弯控制。
斜板有无与斜板不同坡度相比,柱配筋差异很大,斜板对柱配筋影响较大,5个模型中配筋最大差异达到一倍多。
6.3 梁跨中配筋结果对比
对比五个模型中研究榀梁的跨中配筋,梁底部受拉钢筋面积模型5最大,模型1没有楼板,计算的梁底部受拉钢筋次之,模型5的梁跨中正弯矩大于模型1的; 随着坡屋面坡度的增加,斜板对梁跨中的支承作用变强,梁跨中下部正弯矩减小,配筋减小,在模型3,4中已经出现了跨中上部受拉,并且坡度越大,上部受拉面积也越大。差异最大的模型5与模型4相比,受力及配筋已经出现了本质差异,模型5梁跨中底部受拉,配筋88cm2,模型4梁跨中顶部受拉,配筋达到26cm2,坡屋面对于与之相连的梁跨中内力及配筋影响巨大,坡度越大影响越明显。
7 坡屋面对结构指标的影响
7.1 对于周期及周期比影响
通过表1的对比得知,有无楼板对于结构的周期影响较大,坡屋面的坡度大小对于结构周期影响不太大,但是不同的坡度对结构底部剪力影响较大。
7.2 对于楼层刚度比的影响
由于该模型仅仅一层,未具体列出对于刚度比影响的数据。但是由于坡屋面楼层已经失去了正常的层概念,并且无法准确确定坡屋面的层高,层的概念广义化,超出了《建筑抗震设计规范》GB50011-2010(后续简称“抗规”)及《高层建筑混凝土结构技术规程》JGJ 3-2010(后续简称“高规”)对于层刚度比要求的概念,此时必须做出相应的简化处理才能计算出层刚度比。两本规范均按层剪力与层间位移之比计算刚度比,由于无法准确确定其层间位移,会导致斜板层对应刚度很大,宜造成斜板所在楼层的下层或者下几层形成薄弱层,因为斜板竖向分量起到了类似剪力墙的作用。实际设计中可酌情考虑软件计算出的坡屋面刚度比结果,对软件判断可能出现的薄弱层,在设计中可根据概念设计进一步做合理性判断。
7.3 对于楼层位移比的影响
抗规及高规对于楼层位移比均提出了要求。规范对于位移比计算公式是抗侧力构件的最大位移除以平均位移,公式计算前提条件是楼板为强制刚性楼板假定下的变形,或者分块刚性楼板下抗侧力构件的变形,而坡屋面的楼板即使按照全楼刚性楼板假定考虑,程序默认按照弹性模计算,可能存在抗侧力构件最大位移点位移与最小位移点反号的问题,进而导致计算位移比异常,超过规范最大位移比2的限值; 且有坡屋面的结构,结构内力要计算正确,也不应该按照刚性板考虑,要考虑斜板的板面内变形。因此,对于坡屋面层的位移比计算已经不符合规范计算的前提条件,其位移比无参考意义。通过规范要求的位移比控制,无法反应坡屋面层的平面不规则性。
7.4 对结构弹性层间位移角的影响
由于坡屋面建模时需要输入楼层的层高,软件在计算层间位移角时按照对应节点的位移与层高比值得到,因此,坡屋面工程层间位移角的准确计算与否主要取决与层高的确定。而坡屋面由于无准确的层高定位,在前面的论述中,本文虽然提到多种建模方式,可按坡屋面最顶部的高度作为层高输入,也可按柱高加坡屋面层半层高度输入,也可按照柱高输入,坡屋面高按照上节点高建模等,但无论怎么输入,该高度完全是人为赋予,并不能准确确定实际高度是多少,因此,坡屋面结构弹性层间位移角结果不好确定,在设计中建议灵活把握。
8 坡屋面斜板应力分析及拉弯配筋设计
采用PMSAP对于斜板按照中厚板元做有限元应力分析,得斜板在恒、活、风及地震作用下单工况的单元应力,由三向应力状态可计算得到板的名义主拉应力,积分可以得到板沿着主拉应力方向的弯矩与轴力,然后按照拉弯、压弯或纯弯包络得到板的最不利配筋结果。这样的板计算结果不同于设计师正常在PMCAD中按照投影计算的板。
PMCAD中的板,按投影面考虑,对规则矩形房间使用静力手册简化算法计算内力及配筋; 板边界约束仅考虑简支、固结及自由三种情况; 板仅仅是每个房间单独计算,不考虑相邻房间的作用; 板上荷载仅考虑承受竖向荷载,不考虑水平风和地震作用; 并且楼板仅按照纯弯构件进行设计,不考虑板中轴力影响; 同时对于板不考虑相邻楼板影响,也不考虑楼层之间的影响。
PMSAP中的弹性板不仅仅考虑相邻楼层的影响,也考虑本层楼板之间的相互影响,同时考虑风和地震水平力,也考虑真实的梁、柱、墙等对于板的约束,按照拉弯、压弯及纯弯计算最不利的板的配筋面积[9-10]。
选取模型4中的某块斜板,按照PMCAD与PMSAP计算结果做对比,图18,19为PMCAD计算60度斜板对应计算榀投影下板的内力及配筋结果。图20为PMSAP计算该计算榀相连楼板恒载的主拉应力图。图21为对应楼板的配筋计算结果(面积单位为cm2)。图22,23为楼板剖分节点编号图及等效弯矩、轴力结果输出图(在POLY_REI.1输出)。

图18 计算榀相连楼板PMCAD计算的板弯矩

图19 计算榀相连楼板PMCAD计算的板配筋图

图20 计算榀相连楼板PMSAP恒载主拉应力图
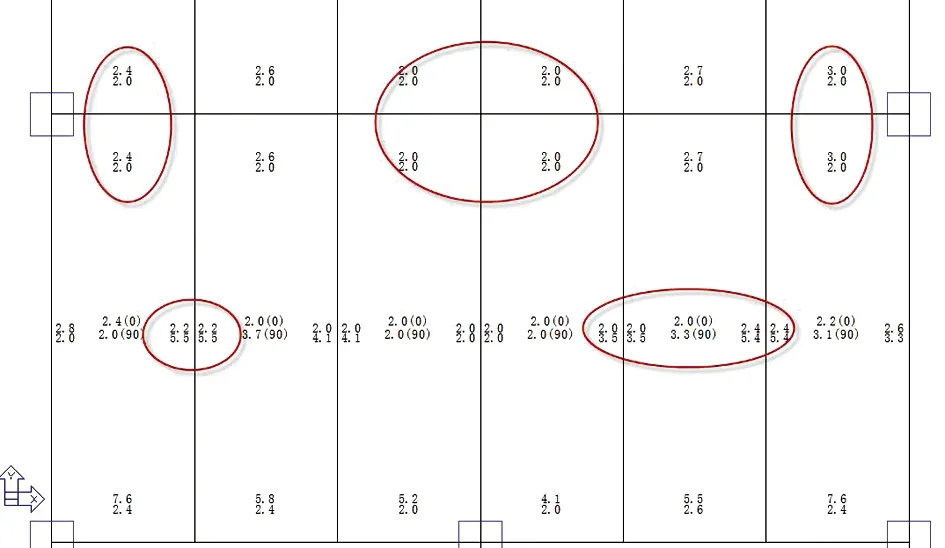
图21 计算榀相连楼板PMSAP计算的配筋面积

图22 楼板网格剖分节点编号图

图23 第2块板等效弯矩、拉力文本结果输出图
通过以上板应力分析结果可得,在恒、活、地震及风荷载作用下楼板中是有等效拉力的,最终板配筋计算是按照拉弯或压弯构件计算得到配筋的。PMCAD与PMSAP计算的楼板的配筋是有较大差距的,对斜板只有考虑真实的约束,并且考虑各类荷载组合,按照拉弯、压弯及纯弯包络设计,考虑斜板真实的作用,配筋才是合理的,该配筋结果可用于指导设计中板的配筋。
9 结语
坡屋面中的斜板,由于既具有水平板的属性也具有竖向墙的属性,与平板受力有较大的区别,对结构整体刚度、内力及指标有较大影响,同时对与之相连梁的受力影响更大,在设计中需正确建模、计算考虑。通过五个模型的对比得出如下结论,供设计人员在设计中参考。
(1)坡屋面的有无对于结构周期、整体刚度、受力均有较大影响,尤其对于与板相连的梁的内力与配筋,如果不正确考虑会得到甚至错误的结果。
(2)坡屋面斜板坡度对结构整体刚度、内力影响很大,坡度变大时会使底部剪力变大,进而影响结构中的梁、柱构件的地震作用,导致配筋增加; 另外随着坡度增大,板对梁的支承作用变强,与斜板相连的梁支座及跨中内力与配筋减小,坡度更大时会导致梁跨中顶部受拉。
(3)坡屋面随着坡度的增大,与斜板相连的梁构件跨中截面、支座轴力逐渐减小,斜梁下柱的剪力也随着楼板坡度的变大剪力减小,斜板对于梁轴力、柱剪力影响较大。
(4)坡屋面由于斜板的作用会导致刚度比、位移比、弹性层间位移角等设计指标异常,在设计中需要根据具体情况灵活把握,按照规范方法计算的结果未必能反应结构真实情况。
(5)坡屋面的斜板具有水平兼竖向刚度,在各种荷载工况下均会产生轴力,应按拉弯构件进行斜板的配筋设计,使用PMSAP对于楼板做整体分析,按应力得到等效弯矩与轴力,再采用拉弯构件进行板的配筋设计。

