上下椽头尾搭接的木构古建筑受力性能的简化计算方法研究

淳 庆，华一唯，张承文，贾肖虎

(东南大学建筑学院，江苏南京 210096)

0 引 言

中国的古建筑木结构体系在世界建筑体系中占有重要地位，历经千百年，具有鲜明的中华民族特色，明显不同于西方以砖石砌体结构为主的建筑遗产类型。中国的古建筑木结构营造传统工艺是工匠按世代相沿袭的手法完成从原材料采集、构件加工制作到安装成型，再到后期装修和修缮的一套完整技术过程，是劳动人民长期实践经验的总结，是经过长时间的反复运用、不断改进和创新而形成的较为成熟的工艺技术体系，蕴含着深刻的科学原理。我国现存的古建筑木结构主要有抬梁木构体系、穿斗木构体系和井干木构体系。这些古建筑木结构随着时间的流逝，受应力效应、环境效应、疲劳效应、腐朽效应以及材料老化等不利因素的影响，不可避免地产生了损伤累计和抗力衰减，一旦材料或结构严重损伤、受强外力作用、自然灾害作用达到一定程度，这些古建筑木结构就存在损毁的风险了。因此，对这些古建筑木结构进行科学的结构性能计算，准确地评估其结构安全现状，尽早地预防损毁的风险，已变得非常迫切了。

目前，国内外学者对于古建筑木结构的结构性能研究主要有以下几方面：在构件研究层面上，徐国明[1]推导出原木椽条在不同荷载组合作用下的最小直径计算公式，并对采用原木椽条的瓦屋面四种常用工程做法进行了总结，编制了杨木原椽条最小直径选用表；赖振中[2]以飞檐为研究对象，介绍了飞檐的历史、形制、艺术价值等，包括早期发展和演变过程、飞檐做法、结构等；井庆升[3]从历史的角度对古建筑翼角的演变进行了总结；一些学者[4-7]对于木梁中出现的叠合做法进行了理论分析与试验研究，得出不同材料、不同尺寸的木梁叠合构件抗弯承载力计算公式。在结构研究层面上，淳庆等[8]通过对南方地区传统的穿斗木构体系和抬梁木构体系的典型榫卯节点和构架的试验研究，得出两种木构体系结构的整体性关键残损点指标；李振等[9]参照宋《营造法式》，建立了单、双、三跨一榀木构架无斗拱有限元模型，对其在相同柱顶配重下进行了低周往复荷载作用下的数值模拟，研究了各自的承载性能；陈春超[10]以榫卯节点、单榀木构架和整体结构的受力性能为研究对象，归纳和总结现有研究成果的不足，结合试验研究、有限元模拟和理论分析对古木结构的整体性能进行了研究；袁建力[11]对墙体与木构架的构造特征、力学性能和布置方案对整体结构抗震性能的影响进行了研究，提出了基于位移控制包括墙体微裂和开裂工作状态的古建筑木结构三阶段抗震分析方法；李小伟[12]以宋代八架椽分心斗殿堂为原型结构，制作了3榀相似比为1∶4的木构架模型，测试得到木材的材料性质和木构架模型在空载、半载和满载3种工况下的动力参数；张海彦[13]以殿堂式木构建筑为例，对其独特的结构形式、节点特性、动力机制进行了研究，提出了榫卯连接特性的刚度公式和等效黏滞阻尼系数。而国外学者[14-17]对木结构的计算研究主要针对采用胶合木为材料的木结构。

综上所述，目前国内外学者对于古建筑木结构受力性能的计算方法研究较少，本研究选取古建筑木结构中的主要结构构件作为研究对象，对常见的荷包木椽、拼合木檩条、木梁架的受力性能计算方法进行研究，最后再从整体上对典型木构架的动力特性进行研究，给出其结构基本自振周期的简化计算公式。研究成果可以为古建筑木结构的结构计算、安全评估、加固修缮设计提供理论依据。

1 结构受力性能简化计算方法

1.1 上下椽头尾搭接的木椽受力简化计算

在古建筑木结构中，木椽是屋面基层的最底层构件，垂直安放在檩条之上，布椽方式多为上下椽头尾搭接(图1)。木椽的类型主要分圆椽、方椽与荷包椽3类。木椽两端搁置在檩条之上，从结构受力的角度可以假设成两端简支的简支梁模型。在木椽受力性能计算时，通常对木椽的抗弯强度、抗剪强度和挠度进行计算分析，以确定木椽的结构安全性。

图1 屋面木椽实景照片Fig.1 Photos of roof rafters

对于方椽和圆椽而言，计算较为简单，本研究不再赘述。在我国江南地区的传统木构建筑中，椽子多为荷包椽。荷包椽的结构安全直接关系到屋面的整体安全，在笔者修缮的数十栋江南地区传统木构建筑中，就存在许多荷包椽挠度过大或断裂的残损现象，究其原因主要是由于断面较小而引起的受力问题所致。对于江南地区传统木构建筑中常见的荷包椽，由于其不规则截面形状，如何求解其截面惯性矩成为计算过程的关键所在。本研究针对荷包椽的截面特性，提出一种简化、快速的计算方法，以便于实际工程中的复核计算。

1.1.1荷包椽截面惯性矩的简化计算 荷包椽是指圆形截面截去直径的1/4所留下的弓形截面，是传统木构建筑中常用的木椽截面形式，如图2所示。为研究其截面惯性矩的简化计算方法，采用组合截面的计算方式计算。计算时，采用整圆的截面惯性矩减去上部1/4弓形截面惯性矩并附加移轴惯性矩，以此得到荷包椽截面的惯性矩。

图2 计算简图Fig.2 Structural calculation diagram

按图2所示的计算简化与参数示意图建立相应的坐标系，首先依据式(1)计算荷包椽截面中性轴位置xc。

(1)

式中，S1、S2分别为整圆截面、弓形截面的面积；xc1、xc2分别为这两个截面自身形心轴相对于x轴的坐标。若假设荷包椽切除的弓形高为h，宽为b，整圆截面的半径为r，那么S1、S2、xc1、xc2可按式(2)至式(5)计算得到，其中弓形的面积和形心位置按抛物线近似估计。

xc1=0

(2)

S1=πr2

(3)

xc2=r-2h/3

(4)

S2=2bh/3

(5)

将式(2)至式(5)代入式(1)可计算得到荷包椽中性轴位置坐标的表达式。

(6)

荷包椽截面惯性矩的计算根据组合截面惯性矩的移轴定理按式(7)计算。

(7)

式中，Ic1、Ic2分别为整圆截面、弓形截面对自身形心轴的截面惯性矩；dc1、dc2分别为这两个截面自身形心轴对荷包椽截面中性轴距离。其均可按式(8)至式(11)计算得到，其中弓形截面惯性矩和按半椭圆近似估计。

(8)

Ic1=πr4/4

(9)

(10)

Ic2=46bh3/945

(11)

将式(8)至式(11)代入式(7)可以计算得到荷包椽对自身形心的截面惯性矩表达式。

(12)

荷包椽截面抵抗矩的按式(13)计算。

W=Ic/ymax

(13)

式中，ymax为荷包椽上下边缘至中性轴距离的较大值，表达式如式(14)。

(14)

当h/2r=1/4时：

Ic≈0.638 8r4

(15)

ymax≈0.932 5r

(16)

W≈0.685 0r3

(17)

1.1.2对檐椽和飞椽的结构意义讨论 1) 宋《营造法式》檐口伸出的规定。《营造法式》卷五中述“造檐之制，皆从撩檐枋心出，如椽径三寸，即檐出三尺五寸；椽径五寸，即檐出四尺至四尺五寸。檐外别加飞椽，每檐一尺出飞子六寸”。也就是说，从撩檐枋心向外至檐口的伸出，由“檐椽出”和“飞椽出”两个距离组成，檐椽出按椽径大小计算，飞椽出按檐椽出的0.6倍计算。

2) 清《工程做法则例》檐口伸出的规定。无斗拱建筑由檐檩中至飞椽外皮的距离，按0.3倍檐柱高计算；带斗拱建筑由挑檐桁中至飞椽外皮(按21斗口计算，其中檐椽出占14斗口；飞椽出占7斗口)。

3) 飞椽。飞椽宋称飞子，它是铺钉在望板上，楔尾形的檐口椽子，与檐椽成双配对，飞椽径与椽子相同，后尾长按出檐长的2.5倍计算。

一般可认为，檐椽由抗弯承载力控制，而飞椽则由挠度控制。下文给出详细计算推导作为依据。

在出挑长度相同的情况下，分两种工况进行计算分析，工况1：仅是檐椽出；工况2：檐椽出+飞椽出。

(1) 工况1。仅是檐椽出时，出挑长度为L1+L2，计算简图如图3所示。

图3 檐椽出挑(L1+L2)的计算简图Fig.3 Calculation diagram of eave rafter with cantilever length of (L1+L2)

此时，最大弯矩为：

(18)

最大剪力为：

V1=q(L1+L2)

(19)

最大挠度为：

(20)

式中,q为木椽均布荷载设计值；qk为木椽均布荷载标准值；E为木椽的弹性模量；I为木椽截面的惯性矩。

(2) 工况2。檐椽出挑L1，飞椽再出挑L2，计算简图如图4所示。

图4 檐椽出挑L1+飞椽出挑L2Fig.4 Calculation diagram of eave rafter with cantilever length of L1 and flying rafter with cantilever length of L2 overhang of eaves-rafter： L1+ overhang offlying-rafter： L2

此时，最大弯矩为：

(21)

最大剪力为：

V2=q(L1+L2)

(22)

最大挠度为：

(23)

经计算比较得，M1>M2，V1=V2，Δ1>Δ2。

计算结果表明，在檐椽的基础上增加飞椽，不仅可以满足建筑外观和构造的要求，而且可以使檐椽的弯矩和挠度均减小，因此檐椽的截面尺寸也可以相应缩小。

表1为檐椽出和飞椽出的最大值，计算时木材强度按照杉木和松木取值，檐椽和飞椽均为方椽，屋面恒荷载标准值取值：琉璃瓦取3.8 kN/m2，筒瓦取3.0 kN/m2，小青瓦取2.4 kN/m2，屋面活荷载标准值取0.7 kN/m2。该表格中的数据可供木椽长度设计时参考。

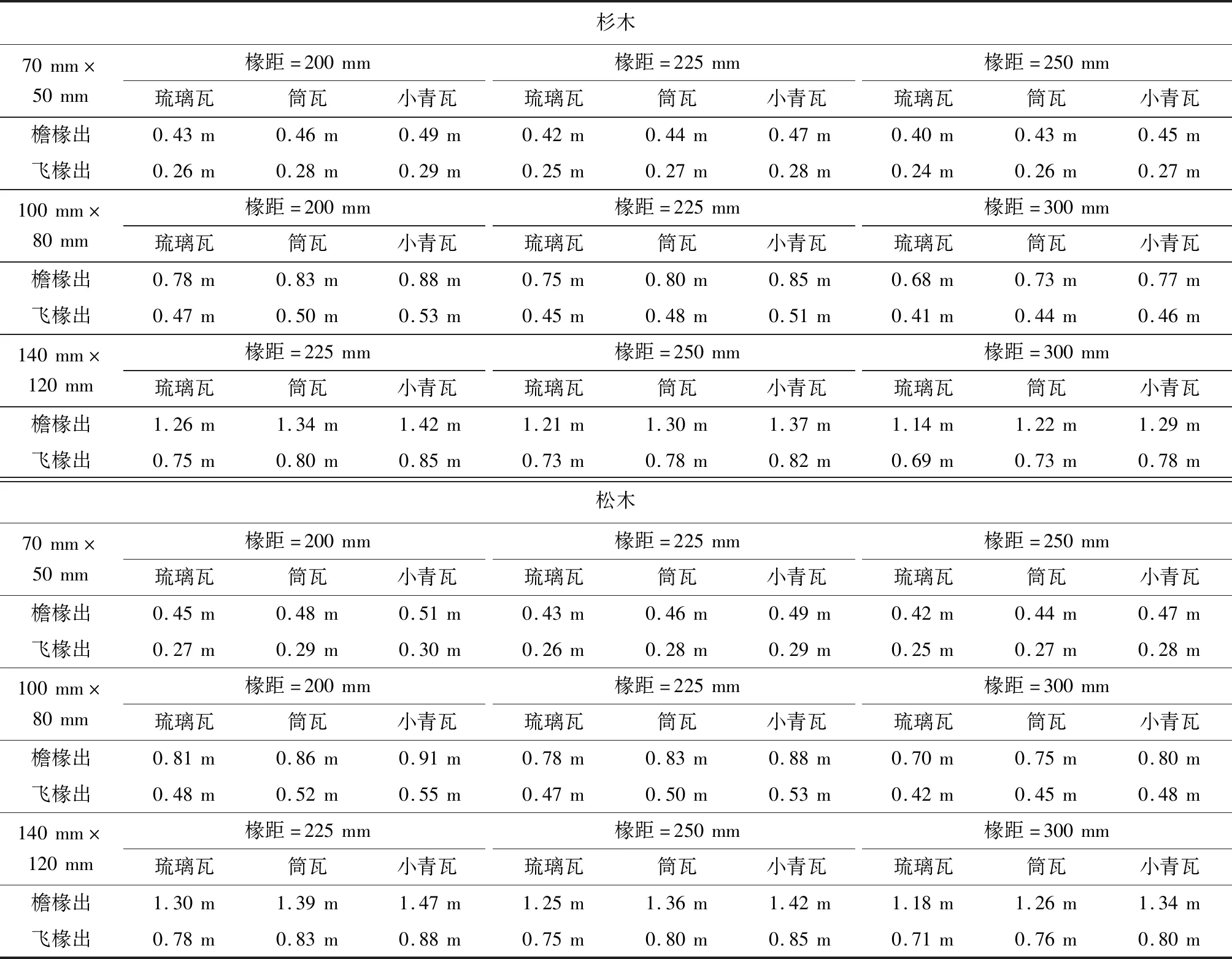
表1 檐椽出和飞椽出的长度最大值Table 1 Maximum cantilever length of eave rafter and flying rafter

1.2 拼合檩条受力简化计算

古建筑木结构的檩条根据位置不同可分为脊檩、金檩、檐檩和挑檐檩等类型，檩条与檩条之间一般用燕尾榫纵向拉接，檩条在跨度较大且受力较大时，为增强檩条抗弯性能，其下方会增设随檩枋(南方又称连机)形成拼合檩条以满足承载力和刚度的要求。随檩枋与檩条之间通常采用近端部硬木销钉的方式进行连接，以形成拼合檩条的结构形式，拼合方式如图5所示。

图5 拼合檩条模型(檩条+随檩枋)Fig.5 Calculation model of stitching purlin (purlin with Fang)

在实际做法中，木结构榫卯节点通常呈半刚性，限制了竖直方向上的位移且具有一定的转动能力。而在进行拼合檩条截面承载力验算时，为留足安全富余度且便于计算，故保守考虑将两端支座简化为铰支座。这时若考虑荷载平衡方程及变形协调条件，再加以檩条与随檩枋的的物理方程，便可求出近端部销栓所受的剪力。

(24)

式中,q为拼合檩条所受均布荷载；d为近端部销栓至拼合檩条端部距离；L为拼合檩条总长度；Du为檩条直径；h为随檩枋高度；A1、A2分别为檩条、随檩枋的面积；I1、I2分别为檩条、随檩枋的惯性矩。檩条—随檩枋拼合檩条的破坏模式可分为两种：1)销栓首先破坏，随后拼合檩条形成叠合檩条，随着荷载的增大，檩条或随檩枋最后破坏；2)拼合檩条率先达到极限抗弯强度而破坏。

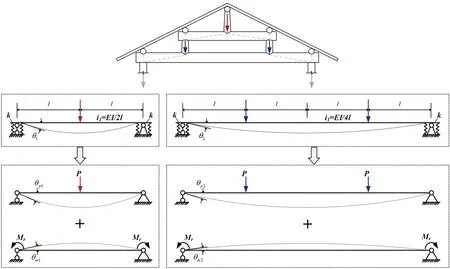
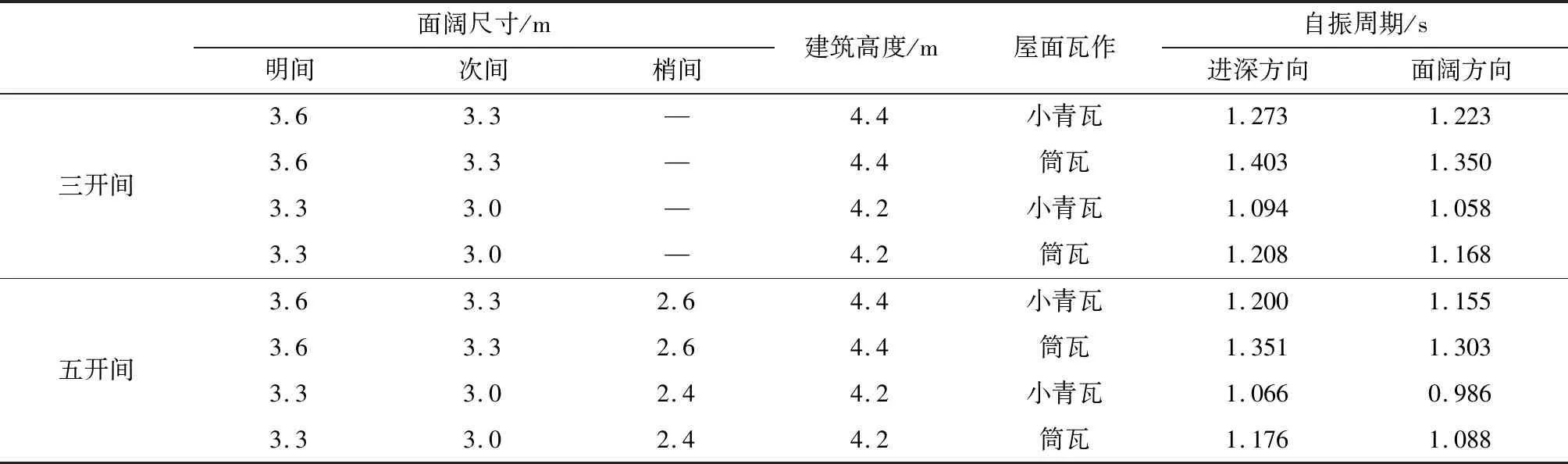
1.2.1破坏模式1 销栓先破坏时，上下小件的极限弯矩满足M1

(25)

式中,A为销栓截面积，其余参量与式(24)中的参量定义一致。在销栓破坏后，形成檩条-随檩枋叠合构件，在小变形情况下，两梁的曲率相同，则拼合檩条最终破坏时最大弯矩为：

当h>Du(随檩枋先破坏)时：

M=M1+M2=2fm(I1+I2)/h

(26)

当h≤Du(檩条先破坏)时：

M=M1+M2=2fm(I1+I2)/Du

(27)

1.2.2破坏模式2 单个小件先破坏时的销栓剪力应满足N<2fvA/3，因此单个小件先破坏时的最大弯矩为：

当h>Du(随檩枋先破坏)时：

(28)

当h≤Du(檩条先破坏)时：

(29)

式中,I1、I2分别为檩条、随檩枋的惯性矩；W1、W2分别为檩条、随檩枋的弯曲截面系数；λ数值为近端部销栓至拼合檩条端部距离d与拼合檩条总长度L的比值。为简化表达引入参量CK，表达式如式(30)。

(30)

1.3 三架梁和五架梁受力简化计算

古建筑木结构民居中的主要受力梁架一般为三架梁和五架梁两种，木梁与木柱的榫卯连接节点根据木构架的不同会有所不同，木梁可以简化为两端半刚性连接的梁，其结果可以视作两端铰支的梁在外荷载与支座反力弯矩相叠加，其叠加原理图见图6。

从图6的叠加原理，有端部转角叠加相等的几何方程：

图6 三架梁、五架梁支座半刚性弯矩计算简图Fig.6 Calculation diagrams for moment calculation of three-purlin beam and five-purlin beam with semi-rigid supports

θi=θpi-θmi(i=1，2)

(31)

若设梁的弯曲刚度为EI，步距为l，则三架梁与五架梁的θpi、θmi可按式(32)和(33)求得。

(32)

(33)

式中,Mr为支座处的弯矩，若设支座处转动刚度为k，其值应为kθ；代入式(31)可解得θi。

(34)

依据Mri=kθi及弯矩叠加原理，容易计算得到支座处弯矩Mri及梁的跨中弯矩Mmi：

(35)

(36)

式中,i为梁的线刚度，对于三架梁计算模型i1=EI/2l，对于五架梁计算模型i2=EI/4l。

对比两端铰支的简支梁跨中弯矩，可以发现当两端支座处考虑榫卯节点半刚性后，跨中的弯矩有所减小，而支座处则出现了一定的负弯矩。为了在工程中方便地计算节点半刚性带来的跨中弯矩折减以及支座处的负弯矩，引入跨中弯矩系数和支座弯矩系数φm、φr，那么跨中弯矩及支座处的负弯矩可以通过简支梁的跨中弯矩Mm0乘以对应的系数得到，即：

Mm=φmMm0，Mr=φrMm0

(37)

依据式(35)和式(36)，容易计算得到φmi、φri的表达式。

对于三架梁：

(38)

对于五架梁：

(39)

1.4 古建筑木结构的基本自振周期简化计算方法

为研究古建筑木结构在两个方向基本自振周期的近似计算公式，针对典型开间数、屋面瓦作及建筑高度的古建筑采用SAP 2000软件建立了有限元模型进行计算分析，其计算模型如图7所示，榫卯节点的转角刚度半刚性数据参见文献[18-20]，木材的弹性模量按常见的杉木和松木考虑，取值为9 000 N/mm2。对于不同的开间数，考虑了三开间、五开间两种常见类型；对于不同的屋面瓦作，考虑了小青瓦和筒瓦两种常见类型，其中小青瓦屋面恒载取2.4 kN/m2、筒瓦屋面恒载取3.0 kN/m2；对于不同的建筑高度，考虑了明间3.6 m和3.3 m两种情况，其余尺寸按古建筑的形制中确定的比例关系推算得到，这两种情况对应的建筑高度分别为4.4 m和4.2 m，柱底为铰接。

图7 不同开间木构建筑计算有限元模型Fig.7 Finite element models of traditional timber buildings with different bays

最终，共获得三开间的4种工况和五开间的4种工况的结构基本自振周期，计算结果如表2所示。

表2 典型木构建筑的基本自振周期Table 2 Basic natural vibration periods of typical traditional timber buildings

从表2中的计算结果可以初步拟合得到典型类型的古建筑木结构在2个方向(进深方向T1、面阔方向T2)的基本自振周期的近似计算公式。

当为三开间时：

T1=η(0.895H-2.665)，T2=η(0.825H-2.407)

(40)

当为五开间时：

T1=η(0.670H-1.748)，T2=η(0.845H-2.563)

(41)

式中，结构基本自振周期单位为s；H为结构建筑高度，单位为m；η为屋面瓦作影响系数，当屋面瓦作为小青瓦时取1，筒瓦时取1.1。

2 结 论

通过从构件层面到结构层面，一方面，对木椽、木檩条、木梁架进行了结构受力计算研究，给出了受力性能的简化计算方法；另一方面，研究了常见开间数的木构架整体动力特性，并给出了其基本自振周期的简化计算公式，研究成果对古建筑木结构的结构受力计算、结构安全评估及加固修缮设计研究与工程实践有一定的参考价值和指导意义。

1) 对古建筑木结构中的荷包椽进行了截面特性的研究，得出荷包椽截面惯性矩的简化计算公式，便于在实际工程中对此类木椽的截面特性进行快速计算。

2) 通过计算分析，给出了工程做法中檐椽与飞椽组合的长度最大值，供设计借鉴参考。

3) 对常见的圆形檩条拼合矩形随檩枋的拼合檩条构件，给出不同破坏模式下的销栓剪力与极限弯矩的简化计算公式，便于在实际工程中进行结构验算和构件设计。

4) 考虑转角半刚性，提出了古建筑木结构中的三架梁、五架梁的跨中弯矩和支座弯矩的计算公式。

5) 给出了古建筑木结构中典型三开间、五开间木构架在进深方向和面阔方向的结构基本自振周期近似计算公式。