一种基于参数标定的投影条纹周期简易校正方法

（内蒙古工业大学 机械工程学院，内蒙古 呼和浩特 010051；内蒙古自治区特殊服役智能机器人重点实验室，内蒙古 呼和浩特 010051）

引言

光学三维轮廓测量在逆向工程、机器人视觉、虚拟现实、医学图像诊断等领域有着广泛应用[1-2]。条纹投影测量法是一种重要的三维轮廓测量技术，具有非接触、全场测量，测量速度快等优点[3-4]。条纹投影三维轮廓测量系统通常需要偏转投影仪的镜头光轴，获得合适的光轴夹角。对于参考平面而言，此时处于倾斜投影状态，需要采用远心镜头投影[5]来保证条纹周期的一致性。如果采用普通镜头进行倾斜投影，则参考平面上条纹周期不再恒定，必然导致相位-高度映射模型复杂化[6]，对后续测量系统标定带来困难[7]。此外，若采用傅里叶变换法也就是傅里叶变换轮廓术[8-9]进行相位复原，会影响频域滤波操作，甚至影响系统测量精度。特别是应用在大视场测量时，这种现象对测量精度的影响会更加严重。

针对上述情况，可通过对投影条纹周期进行校正来解决，许多学者对此进行了研究。当倾斜投影时，若把参考平面上的条纹周期看成恒定值，将会产生高度测量误差。为此，Sansoni 等人[10]提出一个误差补偿算法作为校正措施。Maurel 等人[11]指出参考平面上条纹周期从左向右逐渐增大，如果得到倾斜投射角则可以得到参考面上的条纹周期表达式。Zhang 等人[12]、和Fu 等人[13]在传统二维模型基础上建立了光栅投影模型的方法，提高了测量精度。这2种方法需要事先测量出模型中的未知参数，例如Zhang的方法需要测量出投影仪光轴和摄像机光轴之间的夹角，测量难度较大；Fu的方法需要测量投影仪光心与摄像机光心之间的距离以及投影仪光心至参考平面的距离，由于投影仪与摄像机的光心位置难以确定，所以这2个几何长度的准确测量存在困难。边心田等人[14]建立了双光轴异面情况下的高度计算模型，并在模型中实现条纹周期预校正，主要是为了解决测量系统约束条件问题；但是仍存在类似前面方法的问题，需事先测量3个距离参数。李岩等人[15]提出一种无模型预校正方法，通过投射标准正弦条纹到参考平面，使用傅里叶条纹分析方法复原出非线性相位分布，对比理想线性相位分布反算新的待投影条纹；因为非线性相位分布与空间坐标关系会给相位计算带来误差，并且条纹周期不便于控制。此外也有学者采用后处理技术消除非线性载波影响，如Srinivasan 等人[16]针对未校正条纹利用相位调制技术复原相位，采用相位映射方法得到高度数据。

上面的技术方法能够在一定程度上消除条纹周期非线性变化所带来的误差。然而，处理过程或者复杂、可操作性较差，或者不能完全消除条纹周期误差；多次实验结果的重复性较差，校正效果存在不确定性。本文借鉴反向条纹投影思想实现投影条纹周期校正，以投影条纹图像中各级条纹横向坐标为控制变量推导条纹周期校正理论模型。通过建立实验系统，引入特定光栅图案实现数学模型中未知参数标定，进而生成反向投影条纹；最后通过条纹周期校正实验和三维测量实验进一步验证本文方法正确性和有效性。

1 条纹周期校正理论模型

条纹投影三维测量原理如图1所示，Ep和Ec分别为投影仪的出瞳和摄像机的入瞳。投影仪光轴和摄像机光轴相交于参考面R上O点，二者夹角为φ。投影平面和CCD平面分别与光轴和垂直。经过Op点作参考面R的平行线作为虚拟平面I。

图1 条纹投影三维测量系统示意图Fig.1 Schematic diagram of fringe projection 3D measurement system

由图1可知，投影仪将周期性分布的条纹图像（栅线垂直于投影平面，即平面）投射在参考平面R上，此时参考平面上的条纹从左向右逐渐增大，呈现非均匀变化。要使得R上的条纹为周期性分布，则虚拟平面I上的条纹同样也应该为周期性分布。假设A点为投影平面上任意一点，光线投射在参考面R上于B点，B点在成像系统（即CCD平面）中的像点为Bc点。另外的反向延长线交虚拟平面I于Bp点。过A点作平行于虚拟平面I的直线交光轴于于C点。设投影平面上A点的坐标为Xp，即=Xp，该点在成像系统中对应的像点Bc的坐标为Xc，即=Xc。

另设由 ∆BpOpEp与∆ACEp相似可得

在 ∆ACOp中，根据三角形定理可得

将（2）和（3）式代入（1）式可得

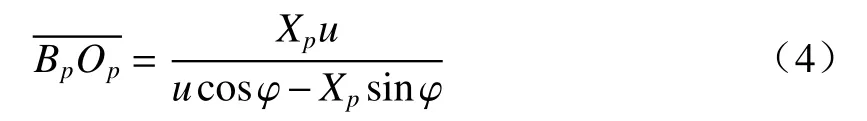
设投影仪与摄像机的放大倍率分别为M1=u和并设再由∆BpOpEp～∆BOEp、∆BOEc～∆BcOcEc得

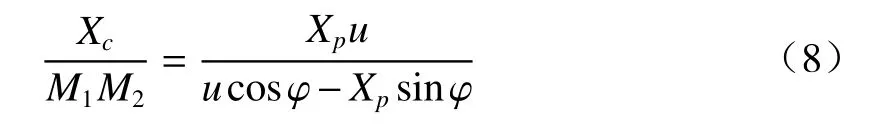
进一步可得

式中：φ、u、M1和M2均为测量系统结构参数或为恒定量，令 sinφ/uM1M2=a，cosφ/M1M2=b，于是（9）式可以简写为

式中：Xp与Xc单位均为像素。上式表明Xp/Xc与Xp呈明确的线性关系。这样将原来的4个系统参数转化为2个组合参数，尽管这2个参数a和b不具有明确的物理意义，但是它却为后续的条纹周期校正提供了极大方便。

（10）式所示的数学模型中的2个参数的确切数值可通过标定方法获取。若得到a和b的数值后，也就建立了CCD平面与投影平面上各级条纹横向坐标之间的关系，即

经投影条纹周期校正后得到的条纹应为周期分布，即Xc与条纹级次为线性关系，因此可以将线性变化的Xc作为输入量，再通过求取反函数计算出待投影条纹坐标：

将其代入下面余弦函数：

便可设计出待投影条纹模式，然后经该系统投影后便得到周期分布条纹。这里Ib和Im分别表示条纹的背景和调制度，f表示条纹频率。

2 模型参数标定

条纹投影实验系统如图2所示，投影仪倾斜投射，摄像机安装在一维平移台上可上下平移。计算机1 控制投影仪加载条纹图像，计算机2 显示和处理由摄像机获取到的条纹图像。实验之前需调整摄像机光轴与参考平面垂直，以及投影仪光轴与摄像机光轴相交于参考平面。具体步骤为：投影仪投影一幅田字格图像至参考平面，田字格目标位于投影平面中心位置；摄像机拍摄参考平面上目标图像并在计算机2 实时显示。打开摄像机控制软件中的十字线（代表CCD 图像平面坐标系），上下一定范围内移动摄像机的过程中，通过调节摄像机位姿使控制软件中的十字线始终与田字格中心线重合，由此完成系统调整。

图2 条纹投影实验系统Fig.2 Experimental system of fringe projection

通过实验方式标定数学模型（10）式中的未知参数时，输入和输出参量为条纹图像中各级条纹的横向坐标。为了方便准确地提取条纹位置坐标，由计算机仿真产生一幅如图3（a）所示的光栅图像，大小为1 309×200像素，包含11条白色栅线，任意两条相邻白色栅线中心之间的距离为130像素。这里指出，投影图像的大小只与显示器分辨率、投影于参考平面上的视场范围以及摄像机空间分辨率有关。将光栅图像投影到参考平面后，摄像机拍摄到的投影条纹如图3（b）所示，大小为1 361×200像素；计算出的条纹间距如图4所示，由图4可见条纹间距从左向右逐渐增加且呈非线性变化，最大最小间距之差为46像素。

图3 未校正光栅条纹图像Fig.3 Fringe images without correction

图4 未校正条纹的间距Fig.4 Spacing of fringe without correction

以图3所示2 幅光栅图像左侧第一级栅线为基准，由此分别获得各级条纹横向坐标Xp和Xc。对Xp/Xc和Xp进行线性拟合后有

式中：a=1.50×10−4，b=1.08。图5给出了计算数据和拟合直线，二者吻合很好，这也进一步验证了上述理论模型的正确性。

图5 理论模型的拟合结果Fig.5 Fitting results of theoretical model

3 投影条纹周期校正实验

获得模型参数后代入（12）式得Xp=Xc/(1.08−1.50×10−4Xc)。其中Xc为线性坐标，由1像素开始，其最大范围结合摄像机空间分辨率、参考平面上投影视场范围等条件给出。进一步代入（13）式可以设计出待投影余弦条纹，设Ib=Im=128，f=1/150，待投影余弦条纹如图6（a）所示，大小为1 300×200像素；将其投射至参考平面，采集到校正后的条纹图像如图6（b）所示，大小为1 381×200像素。校正后条纹间距如图7所示，间距变化不超出均值的±0.1像素范围，说明本文方法能够准确获得周期分布的投影条纹。

图6 校正后投影条纹图像Fig.6 Projection fringe image after correction

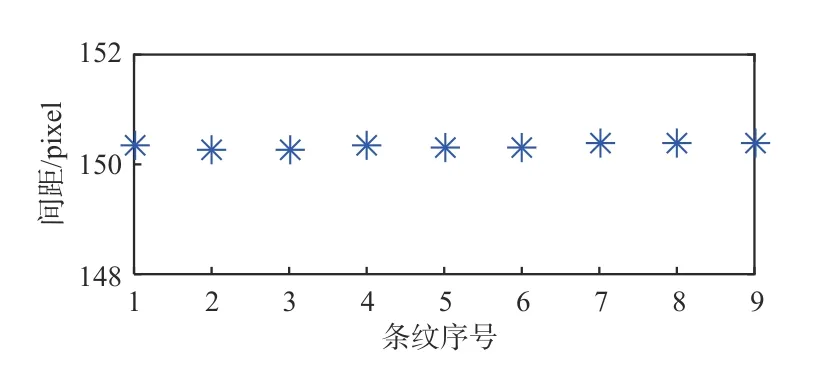
图7 校正后条纹的间距Fig.7 Spacing of fringe after correction

4 三维轮廓测量实验

针对周期校正前后的光栅条纹分别产生四步移相条纹后投影于参考平面。将一个平板作为测量对象，利用四步移相算法求解相位分布。对系统进行标定后恢复出物体高度信息。投影条纹周期校正前后的物体测量结果分别如图8和图9所示。使用精度为0.02 mm 游标卡尺多次测量得到物体的实际高度为8.22 mm；条纹校正前测量结果为7.304 mm，误差为−0.916 mm；条纹校正后测量结果为8.242 mm，误差为0.022 mm，测量误差为校正前误差的2.4%。

图8 条纹周期校正前三维测量结果Fig.8 3D measurement results before fringe period correction

图9 条纹周期校正后三维测量结果Fig.9 3D measurement results after fringe period correction

5 结论

提出一种新的投影条纹周期校正方法，推导出的校正模型只包含2个未知参数，且为明确的线性关系；在系统搭建时，投影仪出瞳与摄像机入瞳连线无需平行于参考平面，放宽了传统方法对测量系统的约束条件。详细介绍了实验测量系统调整以及模型参数标定过程，通过实验在参考平面上获得了周期性分布的投影条纹。该方法原理简单、易于操作、结果准确，可以应用于投影条纹三维形貌测量中改善测量精度、降低系统标定复杂性。尤其是在大视场、条纹数目少的测量场合，该方法的优势和价值将更为明显。