基于区域霍夫变换的机弹分离初始信息提取研究

（南京理工大学 机械工程学院，江苏 南京 210094）

引言

随着战争理念的更新，现代战机更强调高速、可靠性打击、高隐身性能等条件。为了进一步提高战机发射导弹时其自身的安全性和打击的可靠性，机弹分离技术[1-2]开始不断发展。研究[3-4]的主要内容是机弹许可分离，即导弹与载机不仅分离到安全距离才点火，且其点火时导弹的角偏移能控制在一个较小的范围内，使得导弹的命中精度基本不受影响，同时载机的安全性得到保证。目前，国内外对于机弹分离[1-2]的研究手段主要有3种：数值模拟法、风洞试验及飞行实验。相比于高成本的飞行实验与风洞试验，数值模拟法的优势随着计算机技术的提高逐渐凸显出来。其主要是通过计算机来求解出载机与导弹的运动方程，进而研究其特性。目前的机弹分离数值模拟计算过程为：给定初始计算状态，生成网格，求解流场计算气动力，求解导弹运动方程，从而得到导弹的质心运动方程及导弹姿态来分析导弹发射的安全性。由上可知初始计算状态的误差对于最后实际结果的误差有着关键的影响，而目前绝大部分的初始计算状态如初速度、初角速度都只由导弹分离时所受力及力矩的作用粗略计算得出，为了保证仿真结果的精确性与实用性，有必要精确求出机载导弹分离时的初始物理信息。本文提供了一种能实时且精准提取导弹在与弹射挂架分离时的初始物理信息的方案，运用区域霍夫变换对导弹弹身及弹尾的一系列标识圆进行跟踪，再将标识圆的运动转换成导弹运动，从而达到提取导弹分离物理信息的目的。

1 导弹物理信息提取方案

本方案适用于室内导弹弹射试验，可以根据需要添加风洞等条件。导弹可以看成是刚体，其分离运动可以分解为弹体的平动以及弹体绕自身质心的转动。在导弹上添加了一系列标识圆，如图1所示。

图1 标识圆在导弹上的分布Fig.1 Distribution of marking circles on missile

为了简化模型，本文只研究导弹在z-x平面内的运动情况。分别在弹体侧面及弹体的尾部添加3个标识圆（原理图便于查看，实际圆半径要更小），并放置双高速摄像机对弹体下落进行观测。其初始状态如上图所示，以1、2、3 这3个标识圆的观测为例，在导弹未弹射时，过标识圆2圆心平行于y轴的直线与过标识圆5圆心平行于x轴的直线相交于导弹的质心，可以用标识圆2的绝对位移以及其绕弹体转动造成的相对位移求出质心的位移即导弹位移。导弹的位移（xd，zd）和俯仰角θd可表示为

式中：λ为实际导弹尺寸与画面导弹尺寸缩放比；xn、zn为第n个标识圆圆心的位移；−l2·sinθd、l2·cosθd分别为标识圆2 绕弹体转动造成的x、z方向上的相对位移；l2由（3）式给出。

取一极短的时间间隔 ∆t，导弹的速度（vdx，vdz）和俯仰角速度θ′d可表示为

同理通过对标识圆4、5、6 进行跟踪观测可以求得导弹的滚转角 γd及滚装角速度γ′d，同时可计算出l2，如下式所示：

其中R为标识圆2圆心所在弹体圆截面的半径。

2 基于速度的动态区间搜索算法

虽然目前目标跟踪算法[5-8]层出不穷，但其绝大多数都是基于tracking-by-detection的原理进行跟踪。其步骤如下：1）用目标检测算法检测每帧画面中需要的目标，并得到其对应的位置坐标；2）通过某种方式将步骤1）里的检测结果与上一帧的检测结果进行关联匹配，也就是一一对应起来。检测算法分为传统方法以及基于神经网络的深度学习方法。出于时效性的考虑，本方案采取了主流的检测圆及圆心的方法，即随机霍夫变换（RHT）[9]。而一般的数据关联方法是计算两帧中任意2个目标间的欧几里得距离，并取最小值，相应的2个目标被关联，之后使用匈牙利算法来找出最匹配的目标对。但由于导弹弹射时采用的是高速摄像机，其帧率可达到1000 fps，在进行多次重复试验进行数据比对或其他类似情况的时候，短时间内会产生大量的待检测图片。即使采用传统的随机霍夫变换加上一般的数据关联方法也难以保证其检测时效性。为了解决该问题，本文结合KCF[10]（Kernel correlation filter）原理的部分思想提出了一种基于速度确定搜索区间的算法，其依据的是由于高速摄像机的高帧率，前后帧之间的速度矢量变化可以忽略的特点。该算法原理如图2所示。

图2 基于速度确定搜索区间Fig.2 Determine search interval based on speed

假设我们需要检测n个目标，在这里以标识圆为例。首先对视频的前3帧的每一帧进行全图RHT，查找出每个标识圆圆心的初始位置，并通过上文所述的一般数据关联方法对其上下帧的圆进行一一匹配。从第3帧开始，对每个圆给定一个边长均为β·r的矩形搜索框，其中β为矩形框长度系数，r为检测的标识圆半径。假设我们测出标识圆m及其圆心所在的位置(xm,ym)，则由当前帧圆心的位置与上上帧圆心的位置采用平均速度法求出上一帧圆心的速度(vmx,vmy)，由（4）式表示：

式中（x0m，y0m）与（x1m，y1m）分别代表前一帧与后一帧的圆心位置。将其近似为当前帧的圆心速度并假设其保持不变，则可预测下一帧圆心位置在(xm+vmx·∆t,ym+vmy·∆t)附近，把搜索框中心移步到该位置。从下一帧开始，只需要在n个搜索框内（n为待搜索圆个数）进行区域RHT，且无需进行数据关联，就可以进行n个圆的多目标跟踪。步骤流程如图3所示。

传统KCF算法原理是根据原有搜索框的位置将预测搜索框在原有搜索框附近进行循环移位，再使用分类器依次计算响应值，得到最大的响应值就是所求结果。而本文利用了高速摄像机高帧率的特点，将搜索框的下一位置进行较为精准的预测，从而避免了不必要的计算，节省了时间成本，时效性大幅提高。

图3 算法流程示意图Fig.3 Flow diagram of algorithm

3 实验结果及分析

由于真实的导弹弹射试验涉密，故设计了模拟实验来对上文算法进行效果评估。以等比缩小的待测物体来模拟导弹，取标识圆内径r=0.7 cm、外径R=0.9 cm、相邻圆圆心距l=12.7 cm。以上物理量皆根据实际大小等比缩放。实验内容为，在渐变亮度背景情况下对该算法及传统的全图随机霍夫变换加上一般性数据关联方法进行效果比对，其中矩形框长度系数β设为4.0。

3.1 图像处理

原图一般为彩色的且含有较多噪声，需要进行图像处理才能开始目标检测。首先对其进行边缘检测，其算法有Laplacian算子[11]、Sobel算子[12]和Canny算子[13]等。为了满足边缘检测的3个主要标准即低错误率、高定位性及最小响应，本文采用目前效果最好的Canny算子对其进行检测。在边缘检测后为了减少数据量，采用二值化处理，即图像灰度化，处理后效果如图4（b）所示。最后一步是对图像进行高斯滤波[14-15]（必须使用高斯滤波，因为其他的方法如均值滤波都无法很好保留细节部分），以抑制图像中的噪声。对于本算法而言，由于是图像区域性检测跟踪，故图像的处理在给定搜索框内进行便可，处理后的图像如图4（c）所示。

图4 图像处理结果Fig.4 Results of image processing

3.2 视频检测及结果分析

通过对无风环境下室内导弹弹射视频帧分析，可以得到指标如（5）式所示。

图5 视频帧处理结果Fig.5 Results of video frame processing

表1 前3帧的坐标定位Table1 Coordinate positioning of first three frames

由表1可见初始定位的搜索框十分准确，坐标误差不超过1.5%。

处理完前3帧图像后，按算法流程逐帧预估搜索框的位置并进行区域RHT检测跟踪相应标识圆。图5（b）是视频中等间隔取出的3帧原始图像，可以从图像中看出标识圆移动的速度是逐渐改变的，其坐标数据如表2所示。

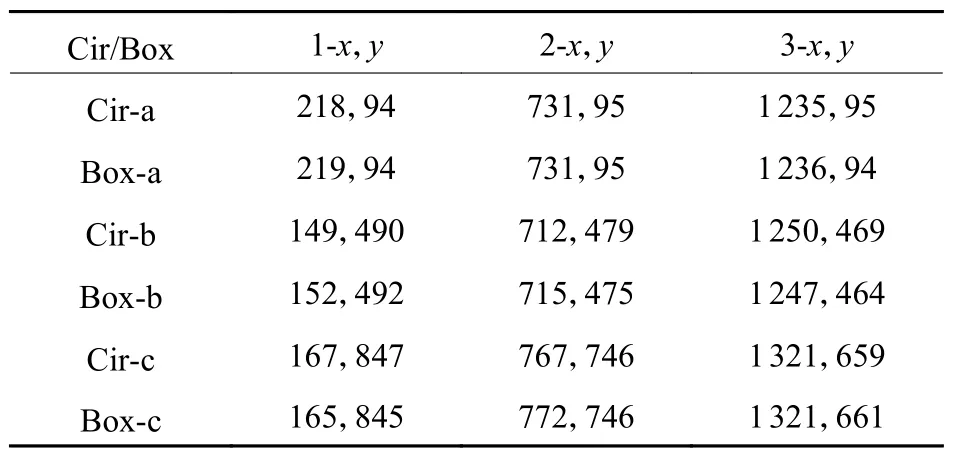
表2 等间隔帧的坐标定位Table2 Coordinate positioning of equally spaced frames

由表2可以看出搜索框中心与圆心的位置十分接近。设搜索框中心与圆心的欧几里得距离为l，标识圆的半径为r，则预测区域的位置误差可以由即相对距离误差来表示。以15帧为步长，从300帧图像中均匀地取出20帧图像，可以得到每帧图像每个标识圆对应的ε，如图6所示。

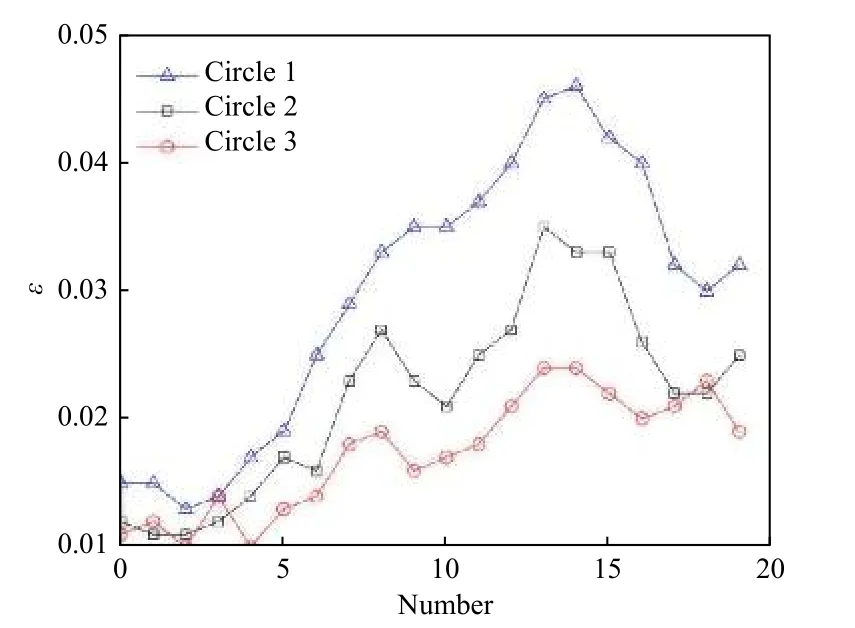
图6 三个标识圆对应的预测误差Fig.6 Prediction errors corresponding to three marking circles

由图6可以看出标识圆1，即左边的标识圆的ε最大，这是因为其速度的变化幅度较其他2个标识圆更大，但其最大相对距离误差不会超过5%，从而证明了预测区域的稳定性较好。

为验证该算法在复杂背景下仍然具有较好的效果，将模拟实验的背景设置为多圆干扰背景，其结果如图7所示。从图7可看出区域RHT 避开了所有的干扰圆，只要矩形框长度系数β选择恰当，背景中的干扰圆一般不会影响区域RHT，故该算法具有较好的复杂背景适应能力。

再比较单帧图像处理时本算法与传统方法的耗时，对比结果如表3所示。

图7 复杂背景下视频帧处理结果Fig.7 Results of video frame processing under complex backgrounds

表3 耗时对比表Table3 Comparison of time consumption

从上表可以看出，相较于传统方法，本算法可以缩短近41.6%的耗时。这在于本算法只对框选区域进行图像处理及霍夫变换，避免了不必要的计算。

3.3 物理信息提取及误差计算

通过本算法得到相应的标识圆每帧所对应的位置后，就可以通过（1）～（3）式来计算出导弹弹射分离初始状态物理信息。算法精度来源于物理定位精度，而物理定位精度由相机的像素精度及RHT的精度共同决定，标识圆越完美，RHT的精度越高，通过观察视频帧，发现相对于像素带来的误差，RHT 带来的误差可以忽略。对于本弹射系统，像素带来的不确定区间为（−0.25 mm，0.25 mm），用1000帧高速摄像机（像素1440×1080）记录真实的导弹弹射运动过程，共采集300帧图像，对机弹分离点所在帧进行物理信息提取。为尽可能减少相机像素带来的误差，取∆t=0.01 s，即间隔10帧。用3种不同型号的导弹挂架进行弹射试验，计算分离点的物理信息及其物理量平均误差 η，如表4所示。

从表4可以看出物理量平均误差最大误差不超过2.39%，随着弹射速度的增大，其误差越小。这是因为弹射速度越大，相邻帧的相似度就越小，像素精度带来的误差就会越小。

以上实验可以证明该算法兼顾了时效性及鲁棒性（抗干扰性），同时在高帧率下，预测区域的稳定性较高，不容易陷入局部最优。

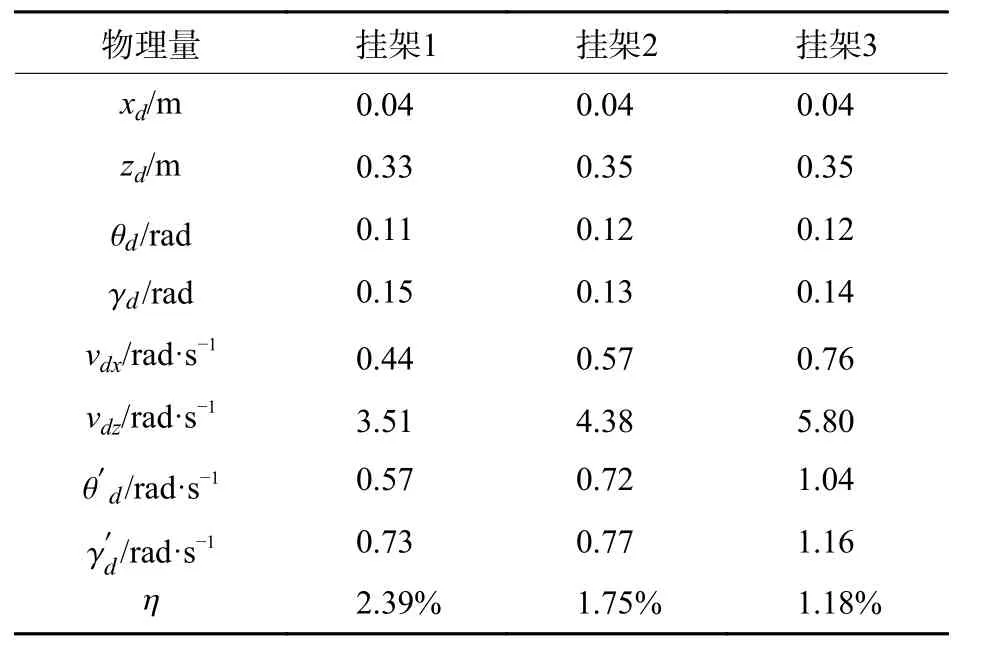
表4 物理量及误差计算Table4 Calculation of physical quantities and corresponding error

4 结论

本文设计了一套关于如何提取导弹弹射分离下落的初始物理信息的方案，其使用高速摄像机对标识圆圆心的位置进行检测，并将其转化为导弹的俯仰角、滚转角、质心位移及其各自对应的速度、角速度等物理信息；同时提出了基于搜索框预测的区域RHT算法，其相比于传统方法性能更优良。应用此方案可以为机弹分离数值模拟技术提供精确的初始条件，减少仿真误差，机弹分离安全性研究的基础更加牢靠，具有良好的应用前景。