高温高湿环境下人体热生理模型的检验及应用
安启启,徐 刚,2,杨 杰,王兴明,朱 辉
(1.西安科技大学 安全科学与工程学院,陕西 西安 710054;2.西安科技大学 西部矿井开采及灾害防治教育部重点实验室,陕西 西安 710054)
0 引 言
“热”是威胁人类健康的职业危害因素之一,尤其是长期从事高温环境下作业的工人更容易患热疾病[1]。研究表明,长期暴露在热环境下作业的工人不仅身体会受到热伤害,还会影响其工作状态和生产效率,甚至造成生产安全事故[2]。因此,人体热生理研究对我国职业危害热防护、人员的热安全性评估以及保障企业的安全高效生产具有非常重要的意义。
自20世纪中期以来,许多研究者开始聚焦于人体热生理的研究,同时开展了一系列的人体热生理实验以发现人体暴露在高温高湿环境下的生理变化特点[3-4]。但由于热生理实验耗时比较长,费用比较高,可操作性不强,且火灾高温辐射场景存在一定热危险性,无法利用真人来展开实验研究[5]。因此,越来越多的研究者开始关注人体热生理模型的建立以预测人体在不同环境温度下的生理反应及舒适性[6-8]。受到国际上广泛认可和使用的是Gagge等提出的两节点模型,该模型将人体分为2个节点(核心节点和皮肤节点),并提出每个节点的热平衡方程,同时该模型中加入了经过简化的热调节机制以控制人体的产热和散热量,进而预测人体的热生理变化,该模型的优点在于简单实用[9-10]。之后,许多研究者为了获得更精确的人体热响应模型,基于两节点模型进行扩展和修正。例如,OOKA等改进了两节点模型中的出汗模型并且验证了改进后的模型在高温环境下的适用性[11]。TAKADA等测试了两节点模型预测皮肤稳态温度的有效性[12];PREK等改进了二节点模型,建立了体现热量和质量在体内传递或转化特性的模型[13]。ZOLFAGHARI等开发了一个新的简化体温调节模型,用于评估人体对瞬态环境的热响应[14]。以上这些改进后的模型在一定程度上增加了模型的精确度,但这些方法大多从某一个方面来改进模型,并且这些模型在能量代谢率输入方面大多取的是近似值,其模糊性较大;此外,以前的热生理模型大都未考虑人体出汗极限,从而使得在高温高湿条件下模型散热较大,与实际情况产生一定的误差[15]。
文中从Gagge两节点模型入手,通过综合考虑暴露在高温环境下作业人员的生理变化特点,分别对两节点模型中的能量代谢率、出汗率、血流速度以及皮肤的最大蒸发热损失等多方面进行改进,建立了改进的人体热生理模型,并通过实验研究对所建模型进行验证和分析,最后利用改进的热生理模型预测煤矿工人的核心温度和安全作业时间,提出职业防护建议,从而确保在热湿环境中作业人员的安全性,降低事故发生。
1 人体热生理模型的建立
1.1 Gagge两节点模型
Gagge两节点模型将人体看成是由2个同心圆柱体组成。外圆柱体代表身体的皮肤层,由皮肤和相关组织组成,内圆柱体代表人体的核心层,由骨骼、肌肉和内部器官组成。核心层和皮肤层的热量传输都服从人体热平衡方程[10-11],两节点模型的计算流程如图1所示。

图1 Gagge模型计算流程Fig.1 Gagge model calculation flow chart
在核心层,人体为了维持自身的体温以及保障正常生理活动,需通过代谢产生热量(M),这些热量主要通过以下方面将热量消耗:人体对外界所做的功(W)、核心层通过热传导以及血液传递的方式将热量转移到皮肤层(Qcr-sk)、与外界进行气体交换损失的热量(Qres),剩余的能量被存储并导致核心温度升高,具体平衡方程如下
(1)
皮肤层的热量传输主要包括与核心层之间的热量传输(Qcr-sk)以及通过对流、辐射(Qc,r)和皮肤蒸发(Esk)与环境之间的热量交换,具体方程如下
(2)
式中m为人体体重,kg;Cb为身体的比热容,(≈3 490 J/kg·℃);t为时间,s;Tcr,Tsk分别为核心温度(指人体身体内部的温度,医学测量中一般以口腔舌下或者直肠温度为参考值)和皮肤温度,℃;AD,α分别为人体表面积(m2)和皮肤质量比(无量纲),可通过公式(3)和(4)计算
(3)
AD=0.202m0.425l0.725
(4)
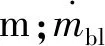
人体通过呼吸损失的热量计算如下
Qres=0.001 4M(34-Ta)+0.017 3M(5.87-Pa)
(5)
式中Ta为空气温度,℃;Pa为人体周围空气中的饱和水蒸气分压,kPa。
核心层主要通过热传导以及血液传递的方式将热量转移到皮肤层,其转移的热量计算公式为
(6)
式中K为核心与皮肤之间的导热系数,W/m2·K;Cbl为血液的比热,J/kg·℃。
皮肤层通过对流和辐射与环境交换的热量如下
Qc,r=ht·(Tsk-To)
(7)
式中To为操作温度,℃;ht为从皮肤到其热环境的总传热系数,W /(m2·K)。
皮肤蒸发热损失(Esk)计算公式如下
Esk=w·Emax
(8)
式中w为皮肤湿润度;Emax为最大蒸发热损失,W/m2。
人体在冷环境中会通过发抖和血管收缩来调节人体热平衡;在热环境中通过血管舒张和出汗来调节人体热平衡,Gagge两节点模型中的温度调节信号模拟了人体在热环境和冷环境下的温度调节机制,这些信号取决于人体每个节点(核心或皮肤)的温度与其相关的中性温度之间的差异。人体对皮肤层和核心层的冷热信号定义如下
WSIGcr=max{0,Tcr-Tcr,n}
(9)
CSIGcr=max{0,Tcr,n-Tcr}
(10)
WSIGsk=max{0,Tsk-Tsk,n}
(11)
CSIGsk=max{0,Tsk,n-Tsk}
(12)
WSICb=max{Tb-Tb,n,0}
(13)
式中CSIG和WSIG分别为人体的冷信号和温信号,下标sk,cr分别为人体的皮肤和核心;Tsk,n为中性皮肤温度(33.7 ℃);Tcr,n为中性核心温度(36.8 ℃)。热中性是指人体每个节点(皮肤和核心)的蓄热量为0。Tb,Tb,n分别为身体的温度以及身体的中性温度,℃,可用公式(14)和(15)表示
Tb=αTsk+(1-α)Tcr
(14)
Tb,n=αnTsk,n+(1-αn)Tcr
(15)
式中αn为人体中性条件下的皮肤所占热量比。
1.2 Gagge两节点模型的改进
1.2.1 被动系统的改进
在Gagge两节点模型中,对于能量代谢率的预测计算主要分为3种。第1种是通过生理实验测量人体的最大耗氧量,然后根据能量代谢率与最大耗氧量之间的经验公式计算得出;第2种根据人体的活动情况,通过国际标准查找近似值;第3种是直接根据能量代谢率的经验公式计算得出。第1种方法虽然能体现个体差异性,但是人体实验耗时较长、费用较高,此外,很多高温热辐射环境无法利用真人展开实验研究;第2种方法模糊性较大,从而误差也较大。综上,利用精确度较高的经验公式预测能量代谢率是相对可靠的,同时有关研究表明,当人在负重及运动条件下能量代谢率会发生变化。因此,基于上述考虑,本研究在Gagge两节点模型中引用PANDOLF等得出的计算人体在负重及运动状态下较为准确的代谢率公式,以模拟人体在高温高湿环境下作业的热生理变化[16],具体公式如下
(16)
式中L为人体负重的质量,kg;V为人体行走的速度,m/s;G为坡度,%;η为地形影响因子,通常取1。
1.2.2 主动系统的改进
有关研究发现,出汗率和血液流速除了受温度信号的影响外,还受到体表面积的影响[17-18],因此,需要在出汗率以及血流速率公式中引入体表面积修正因子,具体公式如下
(17)
(18)
式中Cba为体表面积修正因子,计算如下式
(19)
有关研究指出,人体出汗速率存在上限,且上限值为696 g/h[5]。在热中性条件下可以不考虑该条件,但是在高温高湿环境下需予以考虑。但以前的热生理模型很少将其考虑其中,因此,本研究将该上限值引用到Gagge两节点模型中,使模型更切合实际。此外,身体在实际散热过程中排出的汗液并不是全部蒸发掉,尤其当皮肤湿润度越大时,汗液蒸发效率越低。因此,本研究引用了HAVENITH等提出的汗液蒸发效率与皮肤润湿度关系式[19]
当w≤1时
(20)
当1 (21) 当w>1.7时 ηm=0.05 (22) 式中ηm为汗液蒸发效率。 同时,在Gagge两节点模型中,对于人体表面积的计算通常采用的是标准人体公式,未考虑到性别差异,因此,本模型应用了区分性别的人体表面积公式使模型得到更广泛的应用,具体如下[17] (AD)男性=0.005 7l+0.012 1m+0.088 2 (23) (AD)女性=0.007 3l+0.012 1m-0.210 6 (24) 1.2.3 服装系统的改进 服装对于皮肤的蒸发热损失(Esk)具有显著的影响,由于着装人体汗液是在服装表面或内部织物间蒸发。因此,蒸发同样汗水量的着装者和裸体者感受到的冷却效果是不同的,在Gagge模型中需要考虑着装者的最大蒸发热损失(Emax)[20],具体公式如下 Emax=16.7hc(Psk-Pa)Fpcl (25) 式中hc为蒸发传热系数,W/(m2·kPa);Psk为皮肤温度下空气中水蒸气的饱和分压力,kPa;Fpcl为服装的渗透系数。 Fpcl=1/(1+0.143fcl×hc×Icl) (26) 式中fcl为服装面积系数;Icl为服装基本热阻,clo。 此外,由于Gagge两节点模型中对于人体通过服装与环境进行对流与辐射的热交换计算中的服装有效热阻很难确定,通常取的是模糊值。因此,本研究在Gagge两节点模型中引用同济大学叶海等在提出热平衡数时所用到的关于计算服装与环境进行对流与辐射的热交换(Qc,r)公式[21],该公式将替换公式(7),具体如下 (27) 式中Ia为服装外的空气层热阻,m2·℃ /W;Icl单位为m2·℃ /W。 (28) 式中v为风速,m/s。 文中应用3个案例对模型的可靠性进行检验,前2个案例是根据文中所设实验条件进行模拟验证。案例3是根据高俊勇等研究人体在温度为40 ℃,相对湿度为80%的环境条件下进行重体力劳动时的实验数据对模型进行验证[21]。核心温度、皮肤温度以及出汗量对人体在热环境下的风险性评估具有重要的参考价值,也是人体热生理响应中非常重要的3个参数,因此,用它们来验证新模型的准确性。 人体热生理实验在人工气候室进行,该气候室可根据实验需要设定室内温度和湿度,风速约为 0.05 m/s。选用了10名健康男性大学生作为人体实验的受试者。受试者的信息:年龄20.9± 0.9岁;身高:174.8±4.6 cm;体重:64.8±7.7 kg。实验开始前24 h内,受试者不得进行剧烈运动,不得饮酒、喝咖啡。实验过程中受试者里面穿着短袖短裤,外面穿着普通制服,总热阻约为0.7 clo[20-22]。 高温环境一般指的是 35 ℃以上的生活环境与32 ℃以上的生产环境,并且部分生产行业中环境温度会更高。为验证所建模型在高温环境下预测人体生理参数的适用性,同时考虑实验的安全性,文中在高温环境(40 ℃)下设定相对湿度分别为50%及60%这2个工况。实验开始前,受试者称完体重后在气候室外(室内自然风流环境)静坐15 min以减小环境因素对人体热生理实验的影响。实验期间,受试者暴露在设定工况条件下(40 ℃/60%或40 ℃/50%)的气候室内,并在跑步机上以6.5 km/h的速度行走50 min(劳动强度可视为重劳动)。在此期间,测量他们的皮肤温度和核心温度。实验结束后,受试者离开气候室,回到静坐时的环境下换衣服,最后称体重(此阶段共计10 min)。具体流程如图2所示。 图2 实验流程Fig.2 Experiment flow chart 人体核心温度的测量采用核心胶囊(测量范围25~50 ℃,精度±0.1 ℃)实时监测,人体平均皮肤温度的测量根据ISO标准[23]使用皮肤温度传感器(测量范围-40~150 ℃,精度±0.1 ℃)连续测量颈部、右肩胛骨、左手和右胫骨4点的皮肤温度,然后通过以下公式加权计算[24] Tsk=0.28T1+0.28T2+0.16T3+0.28T4 (29) 式中T为测量部位的皮肤温度,℃;下标为测量部位,对应关系如图3所示。 图3 4点法测量平均皮肤温度示意 (左正面,右背面)Fig.3 Schematic diagram of mean skin temperature measured by four-point method(left front,right back) 2.2.1 核心温度 将不同环境条件下测量得到的人体核心温度与模拟值进行对比,如图4~6所示。 图4 核心温度的变化(案例1)Fig.4 Change of core temperature(Case 1) 图5 核心温度的变化(案例2)Fig.5 Change of core temperature(Case 2) 图6 核心温度的变化(案例3)[21]Fig.6 Change of core temperature(Case 3)[21] 从图4~5可以看出,本模型与实验值较为吻合。通过计算案例1和案例2实验值与模拟值之间的均方根偏差(RMSD)发现,新建模型预测50 min内核心温度的RMSD分别为0.15 ℃和0.23 ℃。图6可以看出模拟值与实验值在前30 min吻合度良好,但是在t=30 min后核心温度突然下降,这是因为人员在该环境下持续30 min跑步出现热应激反应迫于停止实验,30 min到40 min人员处于休息状态[21]。同时,计算了实验值与模拟值之间的最大误差,案例1的最大误差为0.28 ℃,案例2的最大误差为0.41 ℃,案例3中前30 min的最大误差不超过0.3 ℃。综上,新建热生理模型与实验值之间的所有误差均不超过1 ℃,且能在误差允许范围内可靠预测人体的核心温度。 2.2.2 皮肤温度 不同案例下的皮肤温度测量值与模拟值的比较如图7~9所示。 图7 皮肤温度的变化(案例1)Fig.7 Change of skin temperature(Case 1) 图8 皮肤温度的变化(案例2)Fig.8 Change of skin temperature(Case 2) 图9 皮肤温度的变化(案例3)[21]Fig.9 Change of skin temperature(Case 3)[21] 由图7和图8可以看出皮肤温度的模拟曲线在实验测得皮肤温度误差棒范围内,并且由图9可以看出本模型在案例3中也同样适用。计算案例1和案例2下50 min内新建模型预测的皮肤温度的RMSD分别为1.03 ℃和0.78 ℃,其模拟值与实验值之间的最大误差分别为1.37 ℃和1.21 ℃,并且在30~50 min时模拟值更接近实验值。此外,通过案例3检验了本模型在该环境条件下预测人体皮肤温度的适用性,其最大误差为0.74 ℃。文献中指出平均皮肤温度的模拟值与实验值的差值在 1.6 ℃内是合理范围[25],因此可以看出新建热生理模型在预测人体皮肤温度方面较为可靠。 2.2.3 出汗量 本实验测量的累计总失水量与新建模型模拟的累计出汗总量进行对比如图10所示。 图10 失水量的变化Fig.10 Change of water loss 可以看出,2个工况下人体累计总失水量均超过1 kg,模拟值小于实验值。可能的原因有以下2点,①实验测量的受试者累计总失水量是实验后人体净重减去实验前的人体净重,包括准备阶段和收尾阶段受试者在夏季自然通风室内所损失的水分,由于个体差异性不排除受试者在此阶段有汗液损失;②人体在实验过程中通过呼吸以及新陈代谢等需要消耗一部分水分。 随着我国工业的进一步发展,高温高湿作业导致的职业热病已渗透到越来越许多的行业,采矿业就是其中之一。有关研究的现场测试表明,高温矿井的采掘工作面由于地热、采掘机电设备运转时持续放热等原因致使其实际作业环境温度超过30 ℃,可视为《煤矿安全规程》中规定的高温环境,相对湿度大多在80%~90%,甚至恶劣条件下相对湿度可达100%[26-27]。可以看出,采掘工作面是煤矿井下典型的高温高湿作业环境,工人长期在此作业势必会导致一些职业热疾病。因此,有必要利用已通过可靠性验证的热生理模型来预测煤矿工人在该环境下的核心温度的变化,并参考ISO 9886标准[23]中提出的正常人体核心温度的监测限值38.5 ℃(超过该值人体可能会出现一些生理预警或降低工作效率)来预测安全作业时长,从而提出煤矿井下职业防护建议。 本次模拟场景设置为夏季煤矿工人在采掘工作面从事生产作业的场景。为了达到最大安全防护,环境温度设置为《煤矿安全规程》中规定的高温环境界限,即30℃,相对湿度设置为经研究发现大多数夏季高湿煤矿井下的环境条件,即:80%、90%、100%这3个工况;同时,采掘工作面矿工从事的工种按照劳动强度等级分为轻劳动(强度近似于0.8 m/s的步行)、中劳动(强度近似于1.5 m/s的步行)、重劳动(强度近似于1.8 m/s的步行)[28]。 由图11可以看出轻劳动下矿工的核心温度维持在37 ℃左右,属于正常人体核心温度波动范围,说明从事轻劳动的矿工在此环境下受环境条件的影响很小。由图12可以看出随着湿度的增加矿工的安全作业时间在减少,在湿度为100%恶劣环境下中劳动矿工安全作业时间为107 min,湿度在90%~100%之间矿工安全作业时长为107~124 min,湿度在80%~90%之间,安全作业时长为124~149 min。图13可以看出,湿度为100%时安全作业时长为37 min,比湿度为80%和90%分别减少了6 min和4 min,因此当矿工从事重体力劳动时安全作业时长减少,并且受湿度的影响也变小。基于上述分析,为确保人员安全和提高作业效率,并达到最大防护时间,本研究提出如下3点煤矿井下采掘工作面职业热防护建议。 图11 轻劳动作业矿工的核心温度Fig.11 Core temperature of miners for light work 图12 中劳动作业矿工的核心温度Fig.12 Core temperature of miners for medium work 图13 重劳动作业矿工的核心温度Fig.13 Core temperature of miners for heavy work 1)对于从事中劳动作业的矿工,在相对湿度大于90%时,应每工作107~124 min,进行一次简短休息;当相对湿度在80%~90%之间时,应每124~149 min,进行一次简短休息。 2)对于从事重劳动作业的矿工,在相对湿度大于90%时,应每工作37~41 min,进行一次简短休息;当相对湿度在80%~90%之间时,应每工作41~43 min,进行一次简短休息。 3)应定期对不同作业工种的员工开展问卷调查,调查内容包括超过有效作业时间时其生理或心理方面会产生哪些预警信号,如在作业过程中出现类似预警则应及时采取救护措施。 1)基于Gagge两节点模型,对该模型中的被动系统、主动系统以及服装系统进行改进,建立了改进的人体热生理模型。 2)通过人体热生理实验验证了本模型的精确性,结果表明,该模型能较为准确的预测人体的皮肤温度,核心温度等。 3)通过预测矿工在煤矿井下高温高湿环境中持续作业的安全作业时间发现,从事重劳动作业的矿工安全作业时间最短,基本需每工作40 min左右就要进行一次短暂休息,从事中劳动的工人安全作业时间在2小时左右,从事轻劳动的工人受环境影响较小,该研究可为我国煤矿生产作业工序提供科学指导。2 人体热生理模型的检验
2.1 实验方法及流程

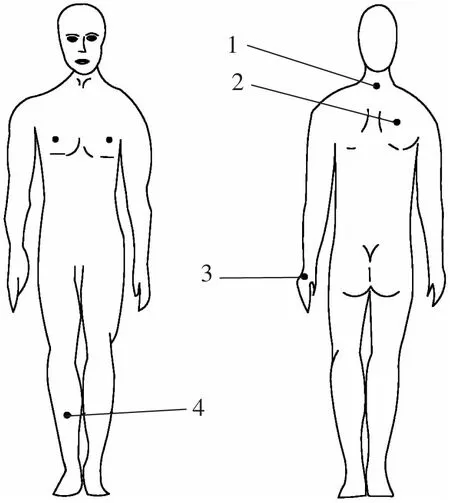
2.2 实验结果及模型检验
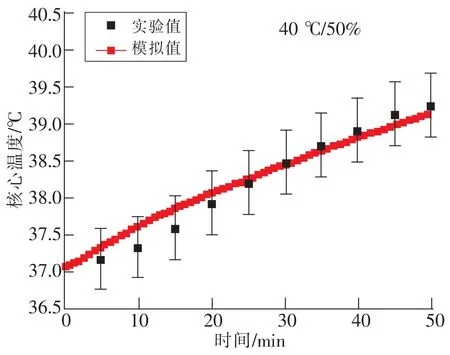


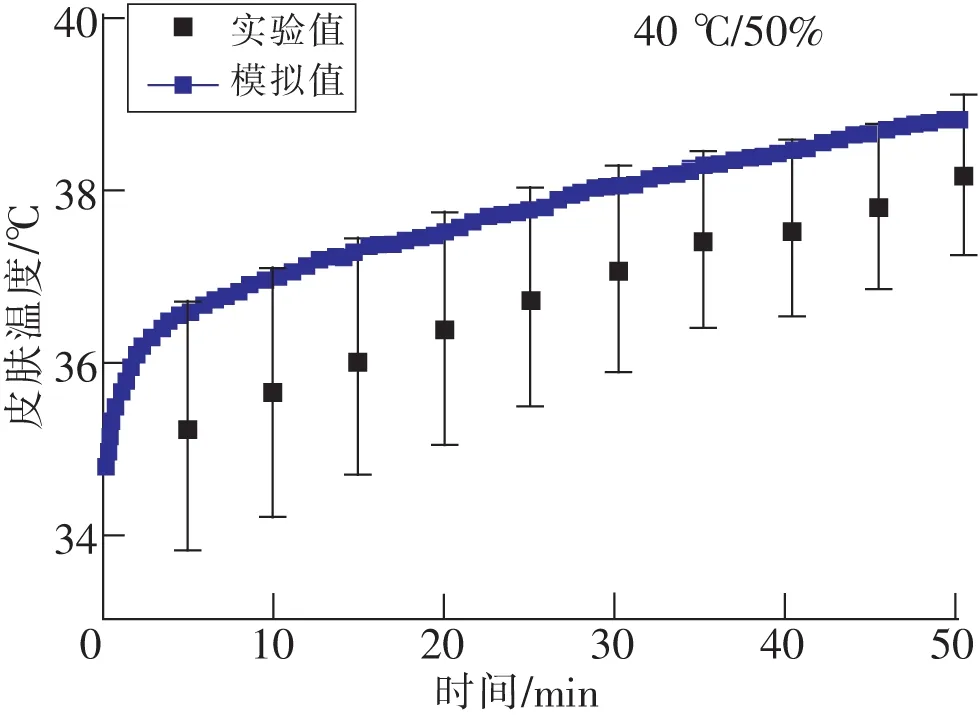
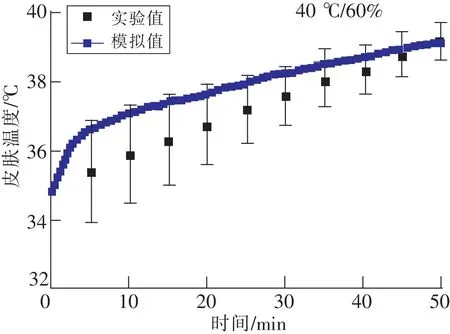
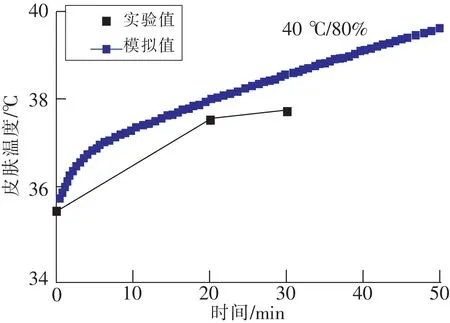

3 模型的应用
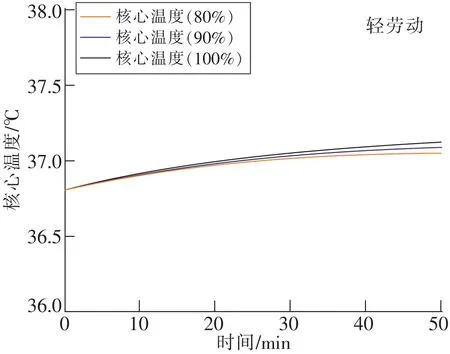

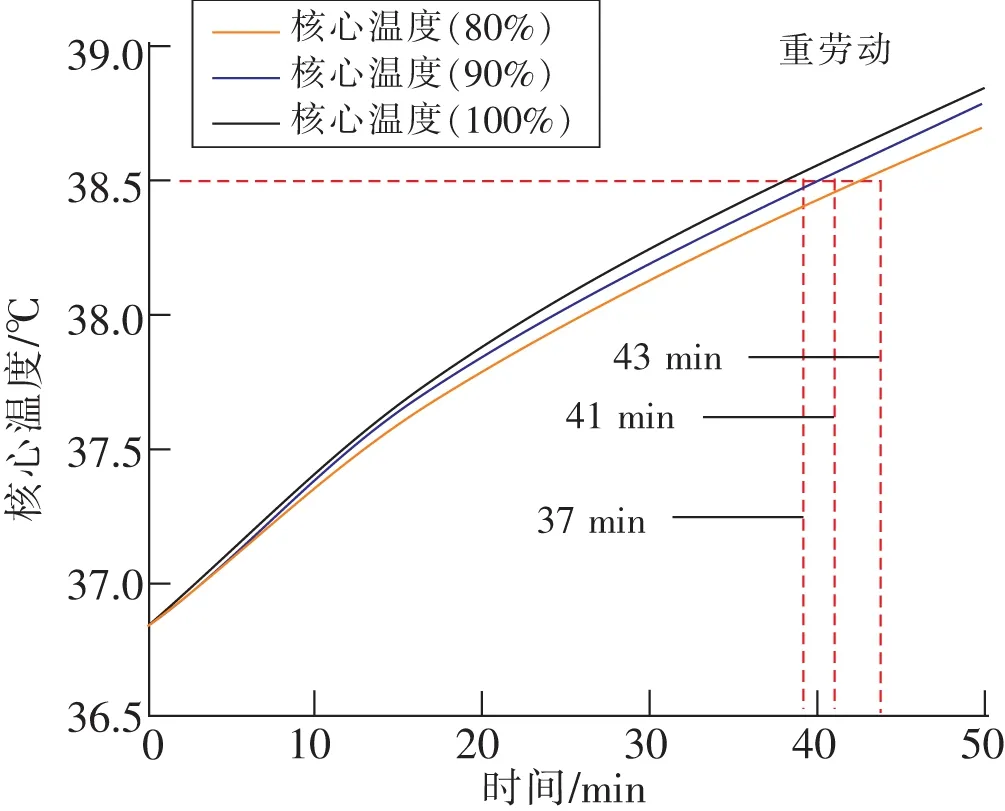
4 结 论

