不同股票风险度量方法的比较研究
——以安徽海螺水泥股票为例
钱礼会,程建华
(安徽大学 经济学院,安徽 合肥230601)
一、引言
中国银行研究院在《2020年度经济金融展望报告》中提到2019年中国经济发展面临复杂的内外部环境,经济下行压力增大。中国经济金融面临了诸多风险,过去十年来的全球银行业总体上都处于一个金融高约束、高风险、高成本的发展环境之中。[1]因此在金融行业中,如何做好风险管理是一项重要的战略性活动,即通过对风险进行识别、评估,并实施有效的控制来减少损失以获得最大安全保障。
弗兰克·奈特在《风险,不确定性和利润》一书中将“风险”定义为可度量的不确定性,通常用数学上的概率来表示,即发生概率不等于0也不等于1,而是存在于0和1之间。[2]霍利则认为风险是企业家的基本属性,企业家是所有实际财富的所有者,而所有权包含着风险。[2]30
市场风险是金融风险的一种,是指因市场价格(利率、汇率、股票价格和商品价格)的不利变动而造成损失的风险。而风险评估作为风险管理的一个关键步骤,需要使用合适的数学模型对风险进行量化,计算出适当的准备金,从而使金融机构在面临经济周期或者日常经济活动中的困难时能够安全度过。[3]度量技术方法也一直在演进,由早期的名义值法、敏感性分析法、波动性分析法,发展到现在比较流行的VaR方法以及压力测试方法。为探究各种不同风险度量方法在股票市场的运用,选取了近几年来收益率一直稳步增长的一只股票,对它进行风险评估。从评估结果的差异对不同的度量方法进行简单比较,从而给投资者或者金融机构在进行投资或风险管理等经济活动时提供参考。
二、文献综述
Wei Jiang等[4]等运用GARCH模型对标准普尔500指数期货收益波动率进行建模,得到了未来波动性与目前的风险损失有很强相关关系的结论。Gupta等[5]运用了几种波动率模型计算了不同时间范围内铜、大豆等七种大宗商品的风险价值,总结出这些商品的VaR异常值与价格的季节性有关,在农产品上更显著。Karmakar等[6]使用了不同市场的不同的股票价格指数,运用CGARCH-EVT-Copula模型,预测投资组合的风险价值和条件风险价值,从而为不同市场建立相应的风险价值有效边界,找到风险资产的最佳投资组合。
在国内,李琳等[7]基于GARCH模型对流动性缺口的风险值进行计算,对不同类型的商业银行面临的风险进行比较,给出了相应的管理建议。徐文彬[8]提到VaR方法是分析和预警系统性风险最有效的模型之一,为使银行业在后危机时代成功转型,测算了12家上市股份制银行的VaR值,分析并提出了我国银行业系统性风险的预警和防范措施。乔瑞中[9]对我国证券市场面临的市场风险进行了探讨,并使用VaR对中信证券风险进行分析,有助于公司对风险进行防范。
以上都是对风险度量进行横向比较,即使用不同模型对风险价值进行计算,比较模型之间的优劣,从而选出最优模型作为衡量标准;或是在基础模型之上进行改进,对特定环境产生更优的结果。而从纵向来看,风险评估的结果是否有显著差异还尚待考究,即各种不同风险度量的方法对某一特定目标是否会产生不同的结果。
三、股票风险理论分析与建模
(一)股票风险
我国股票市场起源于20世纪末,近年来的股票市场越来越庞大,投资也成为国民经济中的重要组成部分。人们放弃即时的消费转而投资是为了获取更高的利益,然而“世上没有免费的午餐”,收益与风险并存,高收益必然意味着高风险。这里所探讨的股票风险指市场风险中的股票风险,即在股票市场上由于股票价格的不利变动而给金融机构带来的损失,风险因素主要为权益证券价格。
(二)市场风险度量方法与股票数据选取
1.敏感性分析法
所谓敏感性分析法,就是找出对收益影响最大的风险因子,通过研究这个关键因子与资产损益之间的关系,进而揭示出风险的大小。通常使用敏感系数即资产损益变动与风险因子变动的比值来表示此影响因子的敏感性强弱。通常用β系数来衡量风险程度,公式如下:

其中ρiM表示第i只股票的收益与市场组合收益的相关系数,σi表示股票的标准差,σM表示市场组合收益的标准差。
2.波动性分析法
传统理论认为市场是有效的,资产的波动恒定,但其实不然。如资产收益率的分布会被假设服从正态分布,而实际分布却会表现出尖峰后尾的特征。均值周围的点比正态分布要高,而尾部也会肥胖一点。另外,市场外部冲击会对资产价格造成一种持续性的影响,这种现象被称为波动集聚性。关于波动性的估计分为两种:静态法和动态法。静态法假定在一定时间内波动率保持不变,使用该样本期的方差。在基于历史数据的动态估计下,可使用移动平均法和GARCH模型。
3.VaR方法
风险价值(VaR,Value at Risk)方法作为衡量风险的标准,自巴塞尔协议II(Basel Committee,1996)采用VaR作为监管资本的基准以来一直受到欢迎。[10]它是指一家金融机构在面临正常的市场波动时,特定资产组合在一定持有期内、一定置信水平下可能遭受的最大损失。这种将风险量化,即可以用具体的数字去衡量资产风险的方法,使得风险价值的应用得以推广。[11]根据估值模型和波动性模型的不同,又可将计算方法分为历史模拟法、蒙特卡罗模拟法与方差-协方差法三种。其中,历史模拟法假定变量未来路径与历史路径一致;蒙特卡罗模拟法假定变量变化服从某个既定随机模型,其中随机游走(Random Walk,RW)是股票走势最常用模型;方差-协方差法假定变量变化趋势服从某个既定分布,如正态分布。
4.压力测试方法
国际证券监管机构组织(IOSCO)将压力测试方法定义为分析最不利市场情形的一种分析方法,如利率突然急升或股市突然急降。压力测试主要分为情景测试(sensitive analysis)和敏感性测试(sce⁃nario analysis)两种。主要区别在于情景测试假设多个风险因素同时变化或极端不利事件发生,而敏感性测试旨在测试单个或少数几个风险因素变动时金融机构的风险承受能力。
房地产行业是国民经济的重要组成部分,水泥作为基建的原材料之一,其价格也随房价的上涨而上调。安徽海螺水泥股份有限公司(以下简称安徽海螺)有着“世界水泥看中国,中国水泥看海螺”的美誉,形成了专业化生产体系和庞大的市场营销网络,一直在稳健地发展,更是在2019年度实现了1570.30亿元的营业收入。查看往年数据发现,该公司近十年的平均净资产收益率都在10%以上,最近两年更是达到了25%以上。而且对比同行业其他股份公司,安徽海螺的风险等级处于一个较低水平。综合考虑公司的盈利能力与风险等级,选取安徽海螺2019年1月2日至2019年12月31日期间每个交易日股票收盘价作为样本数据,一共244个记录①。
(三)风险评价模型
1.GARCH模型
GARCH模型是在ARCH模型的基础上提出的,适用于波动性的分析和预测。一种用过去的方差及其预测值来预测未来方差的自回归条件异方差时间序列模型。当前应用最广泛的是GARCH(1,1)。

其中,回报系数α表示波动性对市场运动反应的灵敏度;滞后系数β表示波动性对市场运动反应的持久性;常数项ω代表波动性长期平均水平,对数据的取值期限长度具有较强敏感性。
2.VaR模型
VaR是基于统计学基本原理、利用统计思想对风险进行估值的一种方法。[12]假设给定置信水平为1-α,则有

其中f(r)是收益率的概率密度,VaR默认用正值表示。
四、实证结果及比较
由于收益率序列相比价格序列更有研究意义,对安徽海螺股票收盘价格取对数差分。画出日收盘价(图1)与日收益率(图2)。通过收盘价序列图可以看出股价有一个明显的上升趋势,而且由收益率的时序图可以看到在前期股价的波动幅度较大,尤其在第60—70个交易日之间,而在后期除了有几次较大波动,平时股价相对稳定。
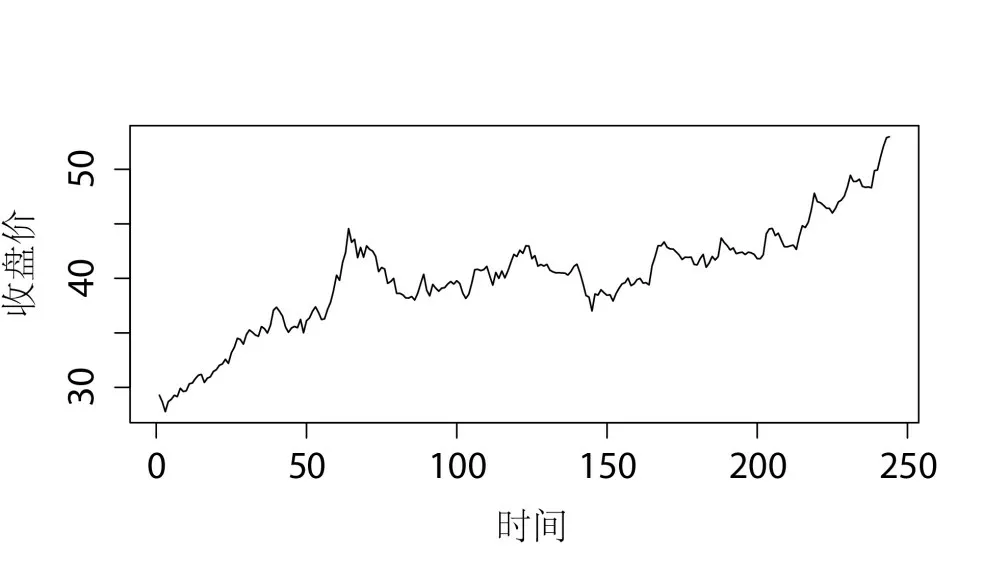
图1 收盘价图
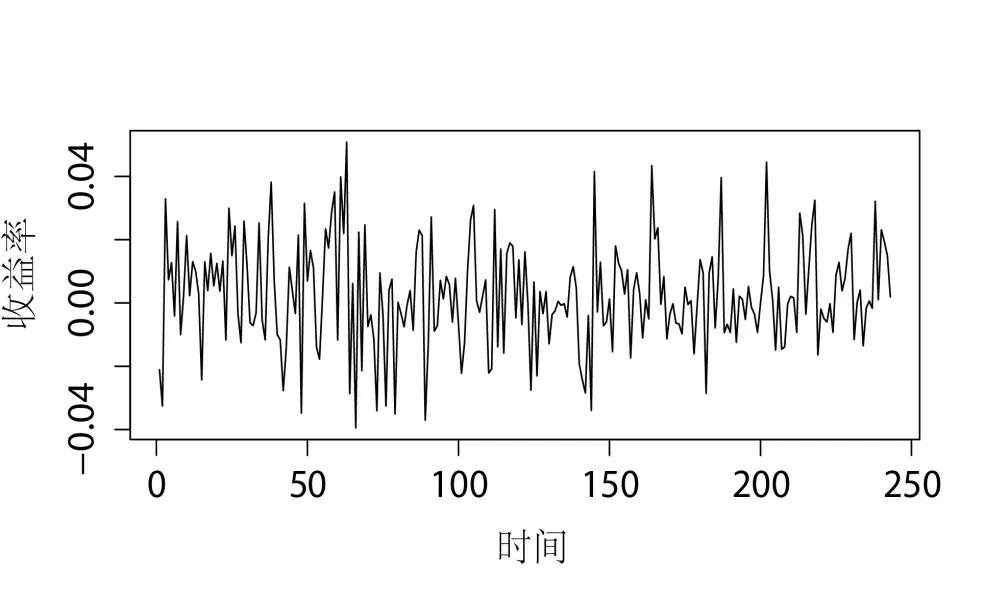
图2 收益率图
对收益率序列数据进行描述统计,得到均值为0.00243,标准差为0.01654,偏度系数为0.11181,峰度系数为3.15659,以及正态分布检验结果的P值为0.69,没有拒绝对数收益率服从正态分布的原假设。平稳性检验结果见图3、图4。
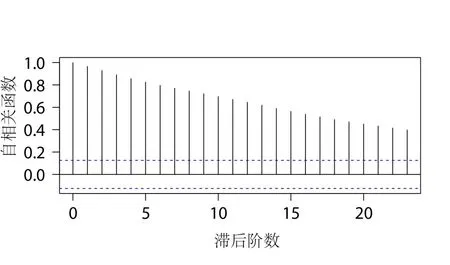
图3 收益率自相关函数图
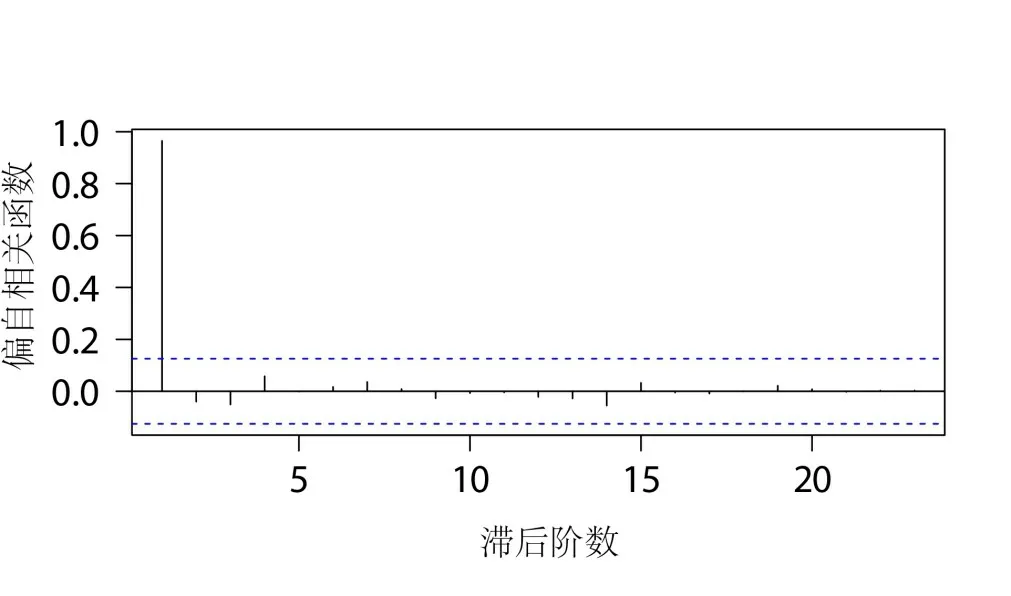
图4 收益率偏自相关函数图
由图3、图4可以看出,自相关与偏自相关的函数值都在一个标准差内上下摆动,可认为收益率序列具有很低的自相关性,满足GARCH模型中的均值方程。继续考察收益率平方项的相关性,结果见图5、图6。

图5 收益率平方序列自相关函数图
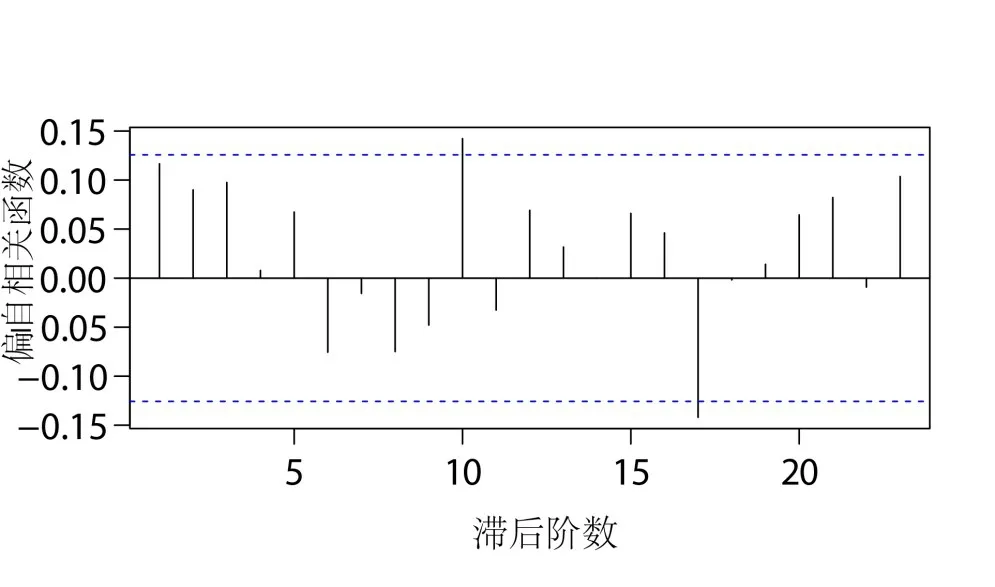
图6 收益率平方序列偏自相关函数图
注意到平方项序列在3阶、10阶之后都有缓慢衰退,可认为平方项序列具有一定程度的相关性。因此可采用GARCH描述股价波动过程中的条件方差。另外滞后10期的LM检验结果P值为0.076,则可以在1%的显著性水平上拒绝认为序列不存在ARCH效应的原假设,即可进行GARCH拟合。可以得到GARCH(1,1)模型拟合参数结果,见表1。

表1 GARCH模型拟合参数
由拟合结果看到所有系数在0.1的显著性水平下拒绝系数为0的假设,说明收益率过去的波动大小对当前的波动具有明显影响,即有波动聚集效应。β系数为0.5,表面条件方差具有一定的记忆性,即波动具有一定程度持续性,投机因素占一半比例,风险稍大。同时,拟合了GARCH(1,2)、GARCH(2,1)、GARCH(2,2),发现模型的AIC与BIC等值并没有显著减少,舍去。对模型结果进行残差分析,同样发现残差序列没有明显波动聚集,且由残差和残差平方自相关图与偏自相关图以及Ljung-Box检验结果P值为0.42,都可以得到原不具有序列相关性,即认为此模型可以有效解释收益率序列。
上述分析是建立在波动性基础上衡量风险,下面使用风险价值方法进行度量。以购买一万只股票作为假定情景进行分析。
在历史模拟法下,逐日股价分布序列上1%位置的值为-1.87,即风险价值为18700元。
使用蒙特卡洛模拟法时,得到收盘价序列ADF检验的t统计量为0.6027,即为非平稳序列。同时由自相关检验结果得到序列存在着明显的自相关性,并且具有滞后一期的偏自相关性。综上可认为收盘价服从随机游走模型。
已知收盘价在最后一个交易日为54.8元,设定随机变量取值范围为(-5.48,5.48)。使用一万个随机数模拟价格变动,计算得到损益序列的1%处的值为-9.47,即由蒙特卡洛计算出的风险价值为94700元。
由前面对数收益率的正态检验结果以及频率直方图,可认为此序列服从正态分布。因此,在方差-协方差方法下,由公式(4)计算得到VaR=ασP0。在计算方差时,考虑静态波动性和动态波动性。静态波动性假设标准差不随时间变化,为0.01654。对动态波动性,在时间窗口的长度为5天、10天、15天的简单移动平均法下,标准差分别为0.02368、0.01953、0.01840。运用指数移动平均法λ=0.94,得到结果0.01612。将以上计算出来的数据代入公式,结果见表2。

表2 不同方差下的风险价值
综合以上计算结果,采用历史模拟法得到的风险价值为18700元,蒙特卡洛模拟法得到风险价值为94700元,方差-协方差法下根据波动性计算方法的不同得到不同的风险价值,其中最大值为5日移动平均30235.57元,最小值为指数平滑20582.66元。由此可以看出蒙特卡洛模拟法计算出的风险价值最大,远远超过其他方法的风险价值,原因在于蒙特卡洛模拟法完全是随机的,没有考虑到历史因素的影响,不确定因素较大。历史模拟法得到的值相比方差-协方差法要小一点,因为历史模拟法赋予历史数据相同权重,而方差-协方差法则对近期的历史数据看得更重。另外由于5日移动平均间隔较短,因此波动较其他方法更大。
五、结论
波动性分析法是根据股价历史的变动轨迹对序列进行建模,由模型的系数对股价往期走势进行分析,该方法既考虑了自身变化,同时也考虑到对市场的反应程度。而VaR方法则是将风险进行了定量化,并求出具体的数值,且所求风险价值只是一个统计上的结果。总的来讲,波动率的分析可以让投资者对股票的变化情况有一个基本了解,而VaR方法则是直观给出了风险的估值。两种方法从不同的角度对风险进行了度量,投资者或者金融机构完全可以结合两种方法对股价的变动以及可能造成的损失在投资行动或风险管理方面做出正确的判断和选择。
在VaR方法的三种不同具体计算方法中,历史模拟法完全依赖于往期的数据,只能适用于市场稳定的情况下,当市场发生重大波动时,就会失去预测效果。蒙特卡洛模拟法全靠随机模型模拟,历史数据失去原本价值。而由于方差-协方差法引入了概率分布,因此计算出来的结果可信度较高,具有很大的借鉴意义。对风险规避者来说,可能更倾向于使用蒙特卡洛模拟法;而对风险偏好者,也许会选择历史模拟法和方差-协方差法来计算风险价值。
需要注意的是,VaR方法最明显的缺陷在于其无法衡量绝对的最大损失,通常我们计算置信水平为99%的风险价值,还有1%的可能亏损会超过风险价值,即存在着尾部风险。此时,需要通过压力测试方法进行风险度量。另外,风险价值是在市场处于稳定即正常情况下所计算出的结果,一旦市场发生了重大波动,VaR方法也就失去了意义。计算风险价值的前提假设是资产组合固定不变,也就是投资组合的规模和结构均不变,然而实际上,资产组合经常会随市场的变动而发生调整,因此限制了风险价值的运用。
注释:
①数据来源:东方财富通Choice数据,股票代码:600585。

