风电场有功功率聚合特性分析及控制策略优化

丛 雨，杨宝峰，尹柏清，刘 宇，翟 寅

（1.内蒙古电力科学研究院，呼和浩特 010020；2.内蒙古自治区电力系统智能化电网仿真企业重点实验室，呼和浩特 010020）

0 引言

随着风电规模不断增大，风电功率的波动对电力系统的影响也越来越大，尤其是风电的大规模集中接入，使得风电功率爬坡问题日益突出，给电网控制带来了巨大的压力。掌握风电波动的内在规律，从风电电源侧提升有功功率输出的稳定性和可控性，是解决大规模风电运行带来的电力平衡、反向调峰、电压稳定、频率稳定等难题的一种研究思路[1]。

本文通过研究风电场有功功率聚合特性及其影响因素，分析风电场功率波动评价指标和方法，提出实现风电场功率稳定输出的优化控制策略，对于风电场并网和提升电网安全稳定运行水平具有重要意义[2]。

1 风电功率波动衡量指标

风电机组集群的聚合功率为各单机功率之和[3]，用式（1）表示：

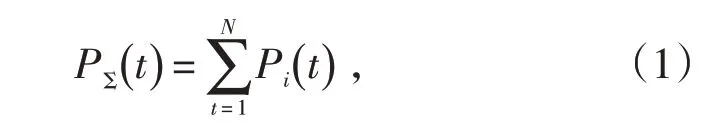
式中：PΣ( t )为t 时刻风电机组集群的总功率；i 为风电机组的编号；N为风电机组数量；Pi( t )为t时刻第i号风电机组的功率。

采用功率序列的标准差衡量单台风电机组功率和风电机组聚合功率的波动性：

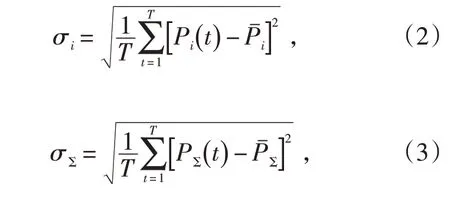
式中：σi、σΣ为第i 号风电机组的功率标准差和聚合功率标准差；T 为统计的时间尺度；、为第i号风电机组功率、聚合功率在相应时间统计尺度下采样值的均值。

功率序列标准差反映了时间序列功率波动程度，数值越小，说明波动越小、平稳性越好。

2 风电场聚合功率波动的影响分析

主要从空间规模上分析聚合风电机组数量及机组功率相关性对聚合风电功率波动的影响。

2.1 风电机组数量对聚合风电功率波动的影响

选择内蒙古某49.5 MW风电场为研究对象。风电场安装33 台额定容量为1.5 MW 的风电机组，风速、有功功率数据采样间隔为10 min。机组间最大间距为3619.5 m，最小为291.8 m。

33 台风电机组某日功率变化曲线如图1 所示，多数机组有功功率随时间的变化趋势相似，但整体上存在一定的幅值差，局部短时间内存在功率变化方向相反情况。图2为该日风电场所有风电机组的聚合功率变化图。对比发现，风电场机组集群聚合功率的波动显著减小。同一固定时段内，选择2 台功率波动最大的机组（21号，33号）与机组集群聚合功率波动情况对比，机组集群聚合功率波动明显小于单机功率波动，如表1所示。

图1 某日风电场内各机组功率变化曲线

图2 某日风电场聚合功率变化曲线

表1 单个机组与机组群聚合功率波动对比

以聚合功率标准差标幺值（即聚合功率标准差与额定功率的比值）衡量聚合功率波动程度，统计4 h 内聚合功率标准差与聚合风电机组数量（累加）的关系（如图3 所示），聚合功率标准差随着聚合机组数量的增加整体减小、局部波动，即随着聚合风电机组数量的递增，聚合功率的波动程度总体为递减趋势，且波动减小的速率下降。

图3 聚合功率标准差与聚合风电机组数量关系

以集群风电机组之间的最大距离表征聚合风电机组群的区域大小，在图3 基础上绘制聚合功率标准差与聚合风电机组群的区域大小的关系，如图4 所示。随着区域直径的增大，聚合功率标准差减小，累计聚合到10 台机组时，机组集群的区域大小没有增大，而聚合功率标准差标幺值略增，表明新增的风电机组功率与前9台机组的聚合功率呈现较大的正相关关系，使得整体波动性略大。

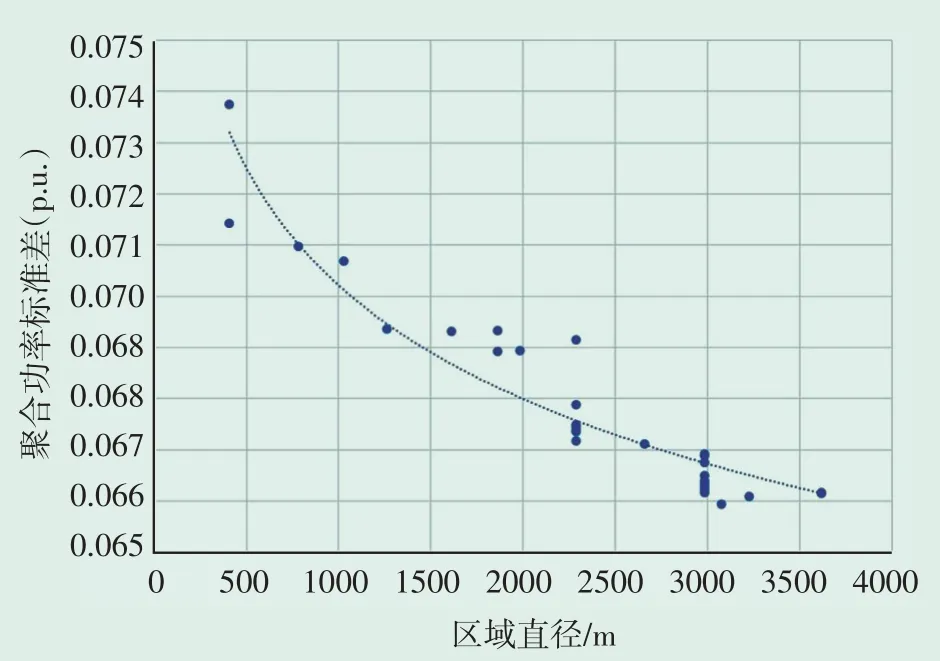
图4 聚合功率标准差与聚合风电机组群区域大小的关系

2.2 功率相关性对聚合功率波动的影响

将两台机组的功率序列看作随机变量X、Y，可计算风电机组两两之间功率的皮尔逊相关系数[4]。皮尔逊相关系数是度量两个定距变量X与Y之间相关程度的变量，大小介于-1和1之间，是以两列数据的协方差与每列数据的方差之比反映其相关性水平，计算公式如式（4）所示：

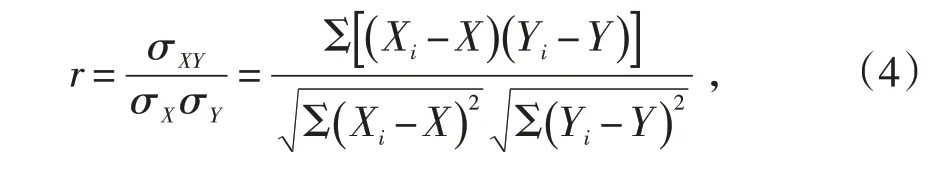
式中：r为相关系数；σXY为两个数据序列X和Y的协方差；σX、σY为X和Y各自的方差。

当r＞0时，X与Y正相关；当r＜0时，X与Y负相关；当r=0 时，X 与Y 不相关；r 绝对值越大，X 与Y 的相关性越大。r仅说明两个变量之间是否存在关系，但并不代表具体关系（如因果关系、线性关系等）。为比较风电机组功率相关性对聚合风电功率波动的影响，以聚合功率标准差标幺值衡量聚合风电功率波动程度，统计4 h 内两台风电机组聚合功率标准差与功率相关系数的关系，如图5 所示。在不同机组间距下，聚合功率标准差均随着功率相关系数的增大而增大，且相关系数在0～0.6时，聚合功率波动增长缓慢；相关系数大于0.6时，功率波动增长加快。这是因为：当两个风电机组功率序列呈现较弱的正相关性时，两者或是幅值相差较大使波动性叠加效果不明显；或是局部存在一定相位差起到轻微“削峰填谷”的效果，中和了波动性叠加效果。而当两个风电机组功率序列呈现较强的正相关性时，两者整体幅值相当，且相位差很小，使聚合功率呈现大涨大落态势，从而增大了聚合功率的波动。

图5 聚合功率标准差与功率相关系数的关系

3 风电机组间功率相关性的影响因素

对于已投运的风电场，重点分析风电机组间功率相关性对聚合功率波动的影响，寻找影响聚合功率波动的因素：在不同机组间距下，聚合功率标准差均随着功率相关系数的增大而增大，且相关系数在0～0.6时，聚合功率波动增长缓慢；相关系数大于0.6时，功率波动增长加快。同时风电机组间的功率相关性反映不同机组功率在时间上的相似程度，受风况和机组间距的综合影响，有必要分析风电机组间功率相关系数与风速、机组间距之间的关系[5]。

3.1 功率相关系数与全场平均风速之间的关系

统计不同距离两台机组间功率相关系数与全场平均风速之间的关系，如图6 所示。不同机组间距下，功率相关系数均随全场平均风速的增大先增大后减小，接着再增大，具体如下。

图6 不同距离两台机组间功率相关系数与全场平均风速关系

（1）第一阶段：在全场平均风速低于启动风速时，有些机组点位风速已达到启动风速，有些机组点位风速未达到启动风速，功率相关性较小。

（2）第二阶段：在全场平均风速高于启动风速时，几乎所有机组启动，功率相关性随风速增大而逐渐增大。

（3）第三阶段：风速继续增加，引起风电场内较强的湍流运动，进而使风电机组功率出现大幅、无序、随机波动，降低了功率相关系数。

（4）第四阶段：全场平均风速增大到额定风速以上，大多数机组保持额定功率运行，功率相关系数上升。

3.2 功率相关系数与机组间距之间的关系

统计不同机组间距下功率相关系数均值与机组间距之间的关系，如图7 所示。不同机组间距下功率相关系数均值在0.4～0.75，机组间距越大，机组点位之间的风资源差异越大，导致风电机组之间的功率相关系数下降。

图7 功率相关系数与机组间距的关系

4 考虑聚合特性的风电场有功功率平稳输出控制方法

4.1 方法简介

对于尚无储能系统的风电场，基本的风电功率波动控制策略是：风电场不按照最大风能捕获要求发电，当风电功率爬坡超过要求时，通过调节风电机组的发电机转子转速和风力机桨距角来控制，但是这种策略以牺牲发电量为前提，在风电功率波动程度较大时可能会导致较严重的弃风限电。根据风电场聚合特性研究，随着聚合风电机组数量的递增，聚合功率的波动程度总体为递减趋势，随着功率相关系数的增大而增大。根据聚合特性的影响分析，考虑风电机组相关性，提出3种风电场平稳输出控制方法，以满足风电场有功功率爬坡率的要求，同时减少弃风限电。

（1）不进行任何爬坡控制，令风电场所有机组按照最大风能捕获要求发电。

（2）当单台风电机组功率爬坡超过要求时，通过调节风电机组的发电机转子转速和风力机桨距角来控制功率爬坡，即对风电场内所有机组逐台进行功率爬坡控制。假定30 min 时间窗口内风电机组功率爬坡量（功率最大值与功率最小值差）超过额定容量的14%，即认为功率爬坡超过要求，需要对风电机组限功率。

（3）考虑聚合特性的风电场平稳输出控制，根据风电场各机组处超短期风速预测信息得出各机组间功率相关性，并进行升序排序，选择功率相关性小的几组作为互补性较好的机组，不对其进行功率爬坡控制；其他机组进行功率爬坡控制。

4.2 方法对比

以风电场12 h 的实际数据为例，方法（3）中根据风电场各机组处超短期风速预测信息得出各机组间功率相关性，对其进行升序排序，选择功率相关性小的6台机组作为互补性较好的机组。

首先，对所有机组两两间的功率相关系数由小到大进行排列。选择功率负相关相关性（-0.59 327）最大的13、18号风电机组作为第一个互补性好的机组对，将其他机组与13、18 号机组的功率相关系数由小到大进行排序。选择前15名（见表2）的交集元素之一的31 号机组作为与13、18 号机组互补性好的机组，由13、18号、31号风电机组组成第一组互补性好的机组群。再次按相关性系数由小到大的顺序选择13、18、31号机组之外的2、4号风电机组，作为第二个互补性好的机组对。重复上述操作，得到第二组互补性好的机组群2、4、22 号。最后选择13、18、31、2、4、22 号这6 台机组作为互补性较好的机组，不对其进行功率爬坡控制，其余机组进行功率爬坡控制。

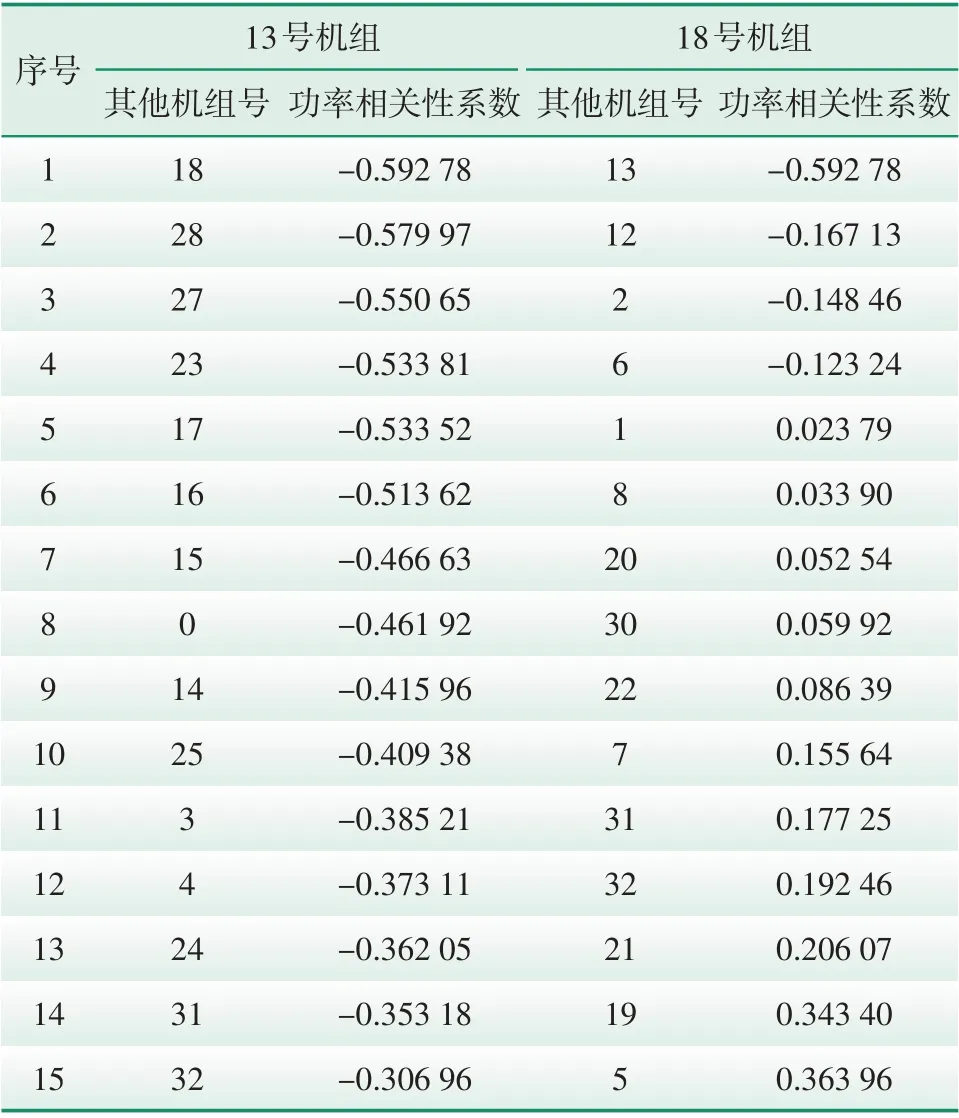
表2 其他机组与13、18号机组功率相关性前15名排序

3种风电场输出控制方法的全场总功率曲线对比如图8所示。无爬坡控制全场总功率高于逐台爬坡控制全场总功率和考虑聚合特性全场总功率；考虑聚合特性全场总功率在波动较小时贴近逐台爬坡控制全场总功率，波动较大时高于逐台爬坡控制全场总功率；逐台爬坡控制全场总功率和考虑聚合特性全场总功率变化幅度均小于无爬坡控制全场总功率。

图8 3种风电场输出控制方法的全场总功率曲线对比

分别计算3种风电场输出控制方法下的全场发电量、30 min 内全场总功率的平均爬坡量和最大爬坡量，结果如表3所示。

表3 发电量、平均爬坡量和最大爬坡量结果对比

由表3可知，在12 h内，无爬坡控制方法的发电量最大，逐台爬坡控制方法的发电量最小，考虑聚合特性控制方法的发电量比逐台爬坡控制方法高7475.3 kWh（1.76%）；逐台爬坡控制方法的平均爬坡量最小，无爬坡控制方法的爬坡量最大，考虑聚合特性控制方法的平均爬坡量只比逐台爬坡控制方法的平均爬坡量高0.78%，各方法30 min 内功率平均爬坡量占额定容量的比值均低于14%；无爬坡控制方法、逐台爬坡控制方法、考虑聚合特性控制方法的30 min 内全场功率最大爬坡量占额定容量的比值分别为14.51%、11.53%和13.18%。由此可见，无爬坡控制方法的全场功率爬坡量最大值超过了14%的限值，而逐台爬坡控制方法和考虑聚合特性控制方法的全场功率爬坡量最大值均满足要求。

根据算例可知，在满足同样的平稳输出要求的条件下，考虑聚合特性选取互补性较好的机组不进行爬坡控制，以其聚合后的平滑效应抑制爬坡，并对剩余机组进行爬坡控制的方法，比全场逐台进行爬坡控制方法的发电量高、弃风限电量少。

5 结语

本文研究了风电场内风电机组位置、数量、机组相关性对聚合功率波动的影响，结合内蒙古电网典型风电场历史运行数据，提出一种以风电场机组间的出力相关性分类的互补控制方法。该方法能够广泛应用于风电场，一定程度提高风电场功率输出稳定性和发电量，并且可在大规模风电汇集区研究分析场群的聚合特性，利用风电场的功率互补性，进一步提高大型风电汇集区功率的可控性，减少清洁能源的弃风限电量。