乙烯装置裂解气压缩机性能预测模型研究
马芳芳, 熊 达, 孙铁栋, 欧阳福生
(1. 华东理工大学石油加工研究所,上海 200237;2. 石化盈科信息技术有限责任公司,北京 100007)
作为乙烯装置的关键设备,裂解气压缩机多采用多级离心式压缩机。在压缩机运转过程中,其性能信息的完备性至关重要。通常压缩机在设计工况下的性能信息由制造商提供,但根据实际生产需要,压缩机常在偏离设计工况的条件下运行。由于实际工况下的工艺参数不可避免会发生变化,所以需要经常对压缩机进行频繁的手动调节,人工干预程度较高,且存在一定的安全风险。为保证压缩机在变工况条件下安全、平稳运行,研究其变工况性能十分必要。
为获取压缩机在各类工况下的性能信息,Sieros 等[1]提出了压缩机和涡轮机性能图的解析表示法,该方法的有效性已在发动机试验中得到验证,但为达到高的精度要求,该方法通常需要引入大量的过程参数,导致模型较为复杂;褚菲等[2]利用热力学定理和压缩机能量损失机理建立了机理模型,并通过BP(Back Propagation)神经网络修正机理模型,虽然该模型的精度较高,但由于离心机操作条件复杂,导致机理模型中的一些重要参数如冲击损失系数等难以准确获取。上述两种模型均较为复杂,工业应用较难实现。Gholamrezaei 等[3]提出了广义旋转回归神经网络算法用于压缩机性能预测,目前该算法仅限于插值应用,外推性即能够准确预测设计工况之外的参数的性能较差;张轩等[4]通过假设一种线性化的压缩机特性曲线关系,采用偏最小二乘法回归,得出压缩机特性曲线模型,但该模型仅适用于正常生产工况下的压缩机性能预测;刘超[5]提出了一种新的模糊神经网络的多级离心压缩机性能预测方法,但其主要对在设计工况下的压缩机性能进行了验证,实际应用效果尚未可知。上述3 种模型因存在外推性差等问题,工业化推广价值有待进一步提升。刘航铭等[6]建立了基于BP 神经网络算法的压缩机组运行模型,但由于传统神经网络存在学习速率低、易于陷入局部最优等缺点致使模型本身存在较大误差,工程应用效果并不理想。综上,上述研究皆专注于模型本身,且建模所用数据多是直接采用设计数据或通过实验获取,而设计数据对应于一定的温度、压力等条件,由其建立的模型直接应用于实际工况时误差较大;实验数据的获取通常耗时较长、成本偏高、数据处理量较大,且受制于实验条件及设备自身性能等因素,因此由其建立的模型在适用性与实用性上存在一定偏差。
针对上述问题,本文以压缩机的设计信息为基础,依据相似理论[7]修正设计数据并建立压缩机压比与多变效率性能模型,基于学习速率自适应误差变化(Learning Rate Self-Adapts Error Change)思想并结合遗传算法(GA)的全局寻优特性提出一种改进BP 算法LR-GA-BP 用于压缩机性能预测,进而将性能预测模型引入ROMeo (Rigorous On-line Modeling with equation-based optimization)[8-10]中进行乙烯装置压缩系统的模拟计算,以期对压缩机在各类实际工况下的平稳运行提供指导。
1 数据的校正与建模
通常用压比 ε 、转速 n 、效率(多变效率) η 和流量(体积流量) Q 四个参数描述压缩机性能,它们之间的关系曲线称为压缩机性能曲线[11]。在一定的温度、压力下,已知任意两个性能参数即可确定压缩机的运行状态[12]。因流量和转速可直接测量,故将压比和效率表示为流量与转速的函数,即建立压缩机压比与效率性能模型,分别如式(1)和式(2)所示。

设计数据是在一定的实验条件下测得的值,为获取压缩机在其他工况下的性能数据,必须对设计数据进行修正。马鹏飞等[13]忽略流体在压缩机出入口之间的密度变化,依据相似理论对流体的质量流率和压缩机转速进行了修正,分别如式(3)和式(4)所示。

其中: Tin和 pin分别为压缩机在设计工况下的入口温度和压力,G 为质量流率,G'和n'分别为修正后的质量流率和转速。本文以上述修正公式为基础,对流体体积流量、质量和压缩机转速分别进行如下修正:
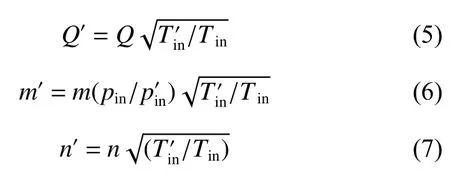

2 改进的BP 算法
2.1 改进BP 算法LR-GA-BP 的提出
人工神经网络(ANN)是一种旨在模仿人脑结构及其功能的智能信息处理系统。作为一种多层次前馈型神经网络,BP 神经网络是目前应用最为广泛的网络模型之一[14]。BP 神经网络的核心是“误差反向传播”学习算法,通过对可变权值的动态调整系统地解决了网络中连接权值的学习问题,但仍存在收敛速度慢、学习速率低和局部最优等缺点。为提高BP 算法精确度和收敛性能,通常是在学习过程中添加动量[15],即:
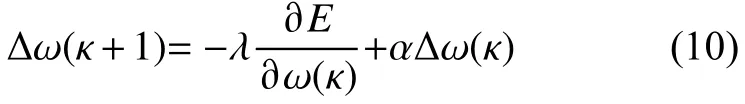
其中: ∆ω 表示权重, λ 表示学习速率, E 表示计算误差, α 表示动量因子(0< α <1,通常取值为0.1~0.8),κ表示计算次数。即若当前梯度方向与前一步的梯度方向一致,则增加这一步的权值更新,否则就减小权值更新。该法能显著提高收敛速度,但在学习速率的选择上较为困难。本文基于学习速率自适应误差变化(Learning Rate Self-Adapts Error Change)的思想引入学习速率的迭代公式,如式(11)所示。
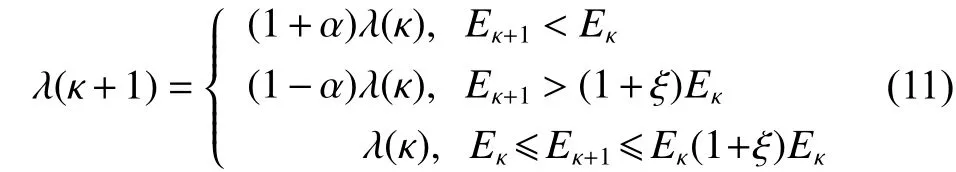
其中: ξ 表示相邻两次计算中较小误差与较大误差的比值,因此有0< ξ <1。式(11)将前后两次计算误差进行比较:若误差减小,则增加学习速率,反之则减小学习速率。为克服传统BP 算法易陷入局部最优的缺点,将GA 与BP 算法进行结合,采用概率化寻优方式,在全局范围内自动获取网络权值的优化区间,提高网络模型的准确性。其结合过程如下:
(1)利用遗传算法随机产生初始二进制字符串结构数据,通过编码及初始化处理得到BP 网络的权值集合。
(2)确定适应度函数。本文选取的遗传算法适应度函数如式(12)所示:

其中: SE是神经网络预测值与实际输出值之间的误差平方和。
(3)选择权值个体。权值个体 i 被选择的概率按式(13)计算:

其中: fi是权值个体 i 的适应度值, l 是总的权值数目。权值个体 i 被选择的概率为 Pi。
(4)交叉和变异
最优权值个体直接进入下一代,其他权值将在网络被选择以后以最初设定的交叉概率( Pc)和变异概率( Pm)进行交叉和变异操作,产生下一代网络。
(5)重复步骤(2)~(4),直至训练结果满足精度要求。
由此得到一种改进BP 算法,即LR-GA-BP 算法。
2.2 实验分析
针对异或问题(XOR),选择典型的三层前馈网络结构,输入层、隐含层及输出层的神经元个数分别是2、2、1。传统BP 算法与改进BP 算法LR-GA-BP的学习结果对比如表1 和表2 所示,可见LR-GABP 性能优势明显,能以更少的迭代步数靠近目标值且误差更小。

表1迭代次数与标准差Table1Iterations times and standard deviation

表2两种算法位运算学习结果比较Table2Comparison of learning results in bit operation between two algorithms
3 压缩机的性能预测及应用
3.1 压缩机性能预测
以国内某石化企业乙烯装置四级压缩机校正后的设计数据作为神经网络的训练样本,利用改进BP 算法LR-GA-BP 对该压缩机性能进行预测。鉴于压缩机输入和输出参数之间的高度非线性关系,建立两个三层的BP 神经网络,通过log-sigmoid 函数[16]生成压缩机输出变量与模式映射关系。具体操作步骤如下:
(1)读取设计数据并进行修正处理。
(2)选择样本数据。以较为典型的第四段设计数据进行说明,压比与多变效率模型分别选择280 组和320 组数据作为训练样本。
(3)利用式(14)对压缩机入口体积流量、压比及多变效率的样本数据进行归一化处理,归一化后的体积流量、 ε′和 η′性能模型各示出20 组数据进行说明(表3)。
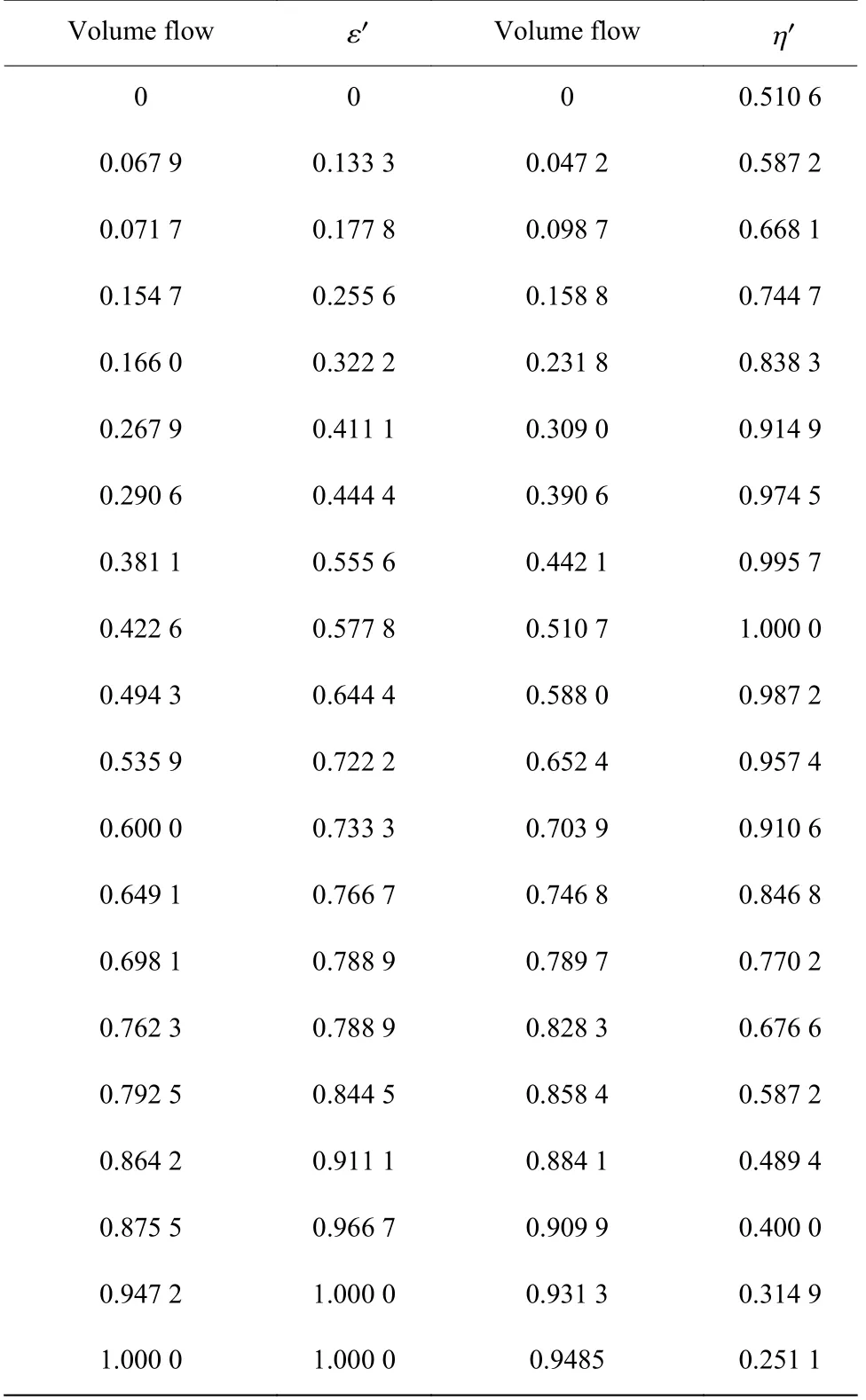
表3归一化样本参数Table3Normalized sample parameters

(4)训练模型并计算各层输出值。压比模型和多变效率模型各表示为一个三层的神经网络,相应输入层、隐含层和输出层的神经元个数分别是2、15、1 和2、16、1。其中,训练误差随隐含层神经元个数的变化关系见图1。

图1BP 神经网络训练误差Fig.1Training error of BP neural network
(5)结合式(11)~(13)调整学习速率与权重;检查网络均方误差(MSE)是否达到精度要求。经过足够的训练,压缩机第四段压比模型和多变效率模型的均方误差分别是 1.75×10−5和 1.5×10−5,符合精度要求。期望值与实际输出值之间的均方误差根据式(15)计算:

其中k 为样本数, Y′(k) 为模型计算值, Y(k) 为实际输出值。
(6)泛化处理:输入新样本,依据模式映射关系输出预测结果。
将非设计转速下的数据代入模型计算,可得压缩机第四段压比与多变效率随修正后的体积流量与转速之间的变化关系见图2 和图3。
3.2 预测结果与模型的应用
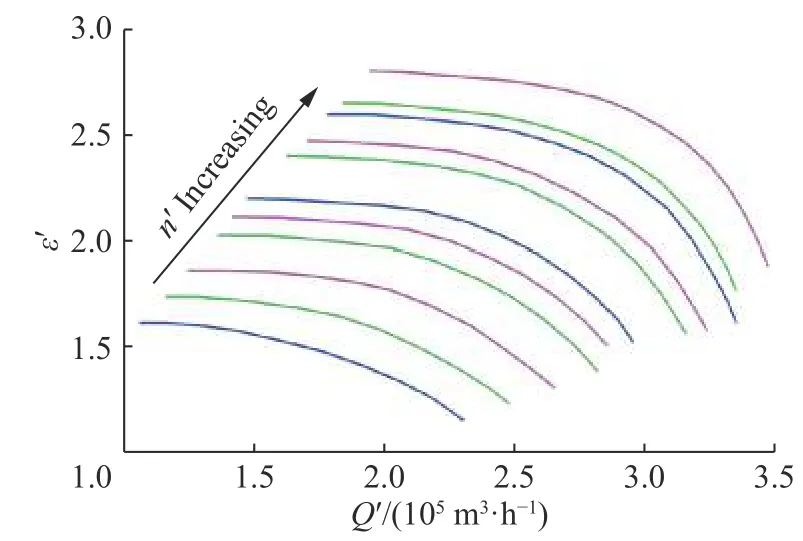
图2压缩机第四段压比Fig.2Pressure ratio of the fourth section of the compressor

图3压缩机第四段多变效率Fig.3Polytropic efficiency of the fourth section of the compressor
以某乙烯装置的裂解气四级压缩系统(图4)为例,该系统由1 个四级压缩机(C100-1ST、C100-2ND、C100-3RD、C100-4TH)、8 个换热器(E101~106、E110、E111)、8 个闪蒸罐(V101~103、V105、V106~109)和1 个碱洗塔(T104)组成,碱洗塔处于压缩机第三段和第四段之间。来自急冷水塔塔顶的裂解气(CG)进入罐V101中闪蒸分离,底部分出的水返回到急冷水塔中,顶部出口裂解气经过压缩、冷却、闪蒸分离、干燥等过程后进入分离单元。WO1~WO4 代表洗油流股,用于降低压缩机入口温度。在ROMeo 中进行压缩系统的模拟计算,建立8 个3 层的BP 神经网络(四段分开建模,每段各建立压比与多变效率两个性能模型),模拟计算时采用SRK(Soave RK)方程,压缩机的相对转速取为0.95。第四段出口气体的主要组分及各段出口温度/压力预测值与实测值的对比结果分别如表4 和表5 所示。
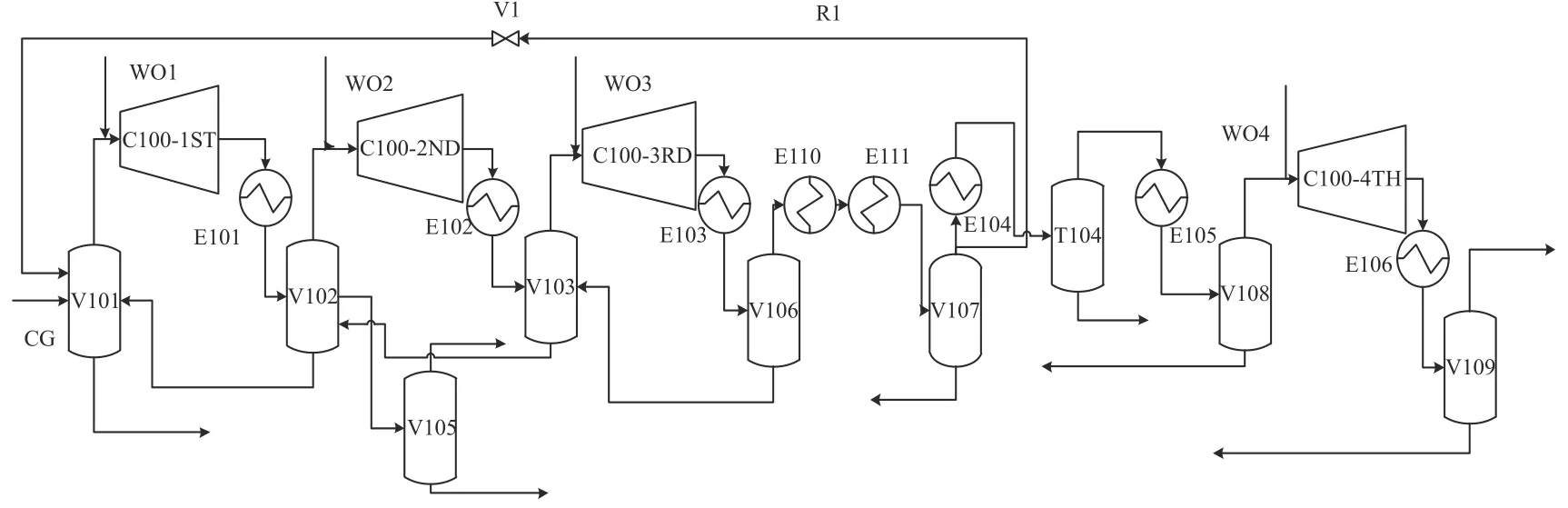
图4裂解气四级压缩系统Fig.4Cracking gas four-stage compression system
由表4 和表5 可知,压缩机第四段出口气体主要组分及各段出口温度/压力的预测值与实测值相吻合,说明所建立的压缩机性能预测模型可靠良好。该系统前三段的出口温度在80~85 ℃之间,第四段的出口温度超过100 ℃。根据工程经验,裂解气中的不饱和烃类在100 ℃以上易于发生大量聚合反应[13],造成烯烃产品严重损失并导致压缩机叶片大面积结焦,影响整个压缩机组的正常运行。经热力学分析可知[17],裂解气的压缩过程可视为绝热压缩,各段出口温度根据式(16)计算。

表4压缩机第四段出口裂解气主要组分预测值与实测值比较Table4Comparison between predicted values and actual values of main components in cracking gas from the fourthstage outlet of the compressor

表5压缩机各段出口温度、出口压力预测值与实测值比较Table5Comparison between the predicted values and actual values of temperatures and pressures in each stage outlet of compressor

其中:Tout和Tin分别表示裂解气压缩机出口温度和进口温度,M 表示压缩级数,K 表示绝热指数。由式(16)可以看出,裂解气压缩机出口温度分别与压缩机入口温度、压比、效率及绝热指数有关。当气体组分一定时,绝热指数为常数,降低压缩机入口温度和压比、提高多变效率可降低出口温度。工程上常采用级间注水或冲洗油的方法降低压缩机入口温度。由图4 可知,为提高压缩机操作裕量,V107 顶部出口设置了返回物流R1,当R1 质量流率改变时,压缩机第四段的压比和多变效率会因入口质量流率的改变而发生变化,进而使得压缩机出口温度发生变化。因此可通过调整R1 的质量流率对压缩机第四段出口温度进行控制。
控制压缩机转速为一定值,对R1 不同质量流率下的四级压缩系统进行了模拟计算。图5 给出了压缩机功耗(Ps)、第四段多变效率和出口温度随R1 质量流率的变化关系。
由图5 可以看出,R1 质量流率由0 增加至6000kg/h的过程中,第四段出口温度逐渐降低,尤其是当R1 质量流率由4000kg/h 增加至4500kg/h 时,温度下降了7.3 ℃;压缩机功耗在R1 质量流率增加的过程中基本不变;第四段多变效率随R1 质量流率的增加呈现先增加后略微降低的趋势,且在4500kg/h处取得一个较高效率值66.24%。即在此模拟条件下,R1 流股较为适宜的质量流率为4500kg/h。
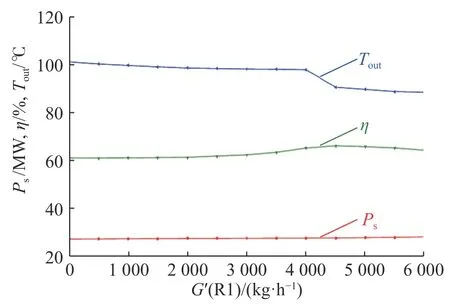
图5压缩机功耗、第四段多变效率、出口温度与R1 质量流率的关系Fig.5Relationship among power consumption, the fourth polytropic efficiency, the outlet temperature and R1 mass flow rate of compressor
由此说明,控制压缩机转速为一定值,在一定范围内增加返回裂解气的质量流率,可有效降低压缩系统出口温度,进而减缓结焦。
4 结 论
(1)以压缩机出厂时的性能数据为基础,依据相似理论修正设计数据并建立了压比与多变效率性能模型。
(2)提出的基于学习速率自适应误差变化思想并结合遗传算法全局寻优特性的改进BP 算法LR-GABP 能以更少的迭代步数和更高的精度靠近目标值。
(3)引入LR-GA-BP 算法对某乙烯装置四级压缩系统进行模拟计算,结果表明模型可靠性良好。
(4)通过压缩机性能模型分析了压缩机第四段出口温度较高的影响因素,并提出了降温措施,对减缓压缩系统结焦、优化压缩机操作具有重要的参考作用。

