直升机机载北斗设备的随机振动分析

连海涛，李刚磊，李柱领，张晓博

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.西安卫星测控中心，陕西 西安 710000；3.中国人民解放军61711部队，新疆 喀什 844000；4.中国人民解放军32034部队，四川 成都 610500)

0 引言

随着北斗卫星导航系统的不断完善和发展，具有北斗通信导航功能的终端设备逐渐在航空领域发挥作用[1]。机载北斗设备在直升机平台上稳定及可靠工作是保证直升机准确定位及通信的前提，如何保证设备在直升机振动环境下稳定工作是设备研制极为关注的。

文献[2]指出，飞机起降和使用过程中，机载设备会受到各种各样的振动与冲击，因此设备会发生故障，并且同时针对螺旋桨飞机安装使用的机柜进行模态分析及随机振动分析。文献[3]结合设备动载振动试验要求，采用有限元软件建立了以壳单元为主的机柜有限元模型。文献[4]采用Ansys软件建立了机载设备安装架的有限元模型，对其进行模态特性分析及优化设计。文献[5]针对车载电子设备使用环境，使用Ansys软件对印制板组件进行随机疲劳分析、计算疲劳系数，给出了随机疲劳分析的方法和步骤。文献[6]针对直升机机载电子设备的PCB板振动试验中出现的故障情况，采用三维建模及有限元进行模态及随机振动动力学验证。文献[7]采用信号分析方法将混合振动分离，进行均衡处理后输出给振动台的控制系统。

随着设备更新换代及外部竞争的不断加大，设备的研发周期越来越短，需要结构设计在研发阶段就能够进行仿真分析，校核设备结构强度，力争做到后期振动试验一次通过，缩短研发周期，节约成本。利用有限元分析方法，模拟仿真机载北斗设备在相应振动环境下的受力情况，成为分析校核设备强度的重要手段。

针对直升机机载设备结构，阐述了直升机振动环境特点，针对其正弦加随机的振动环境，提出利用能量等效的方法将正弦振动转换为窄带随机振动，形成纯随机振动谱，输入至Ansys软件进行仿真分析，获得结构的位移应力响应，校核结构强度。

1 直升机振动环境

直升机运输货物的振动特性是在低量级连续宽带随机振动背景上叠加强烈的窄带峰，这种环境是主旋翼和尾桨以及旋转机械引起的许多正弦或近似正弦的分量与气流流场引起的低量级随机分量的组合[8]。正弦振源频率相对较低，一般为kΩ(Ω为旋翼或尾桨的工作转速频率，k为桨片的数量)及其各阶倍频(一般只取前4阶，忽略高阶分量)[9]。GJB 150.16A-2009中规定的直升机振动环境试验谱图如图1所示。

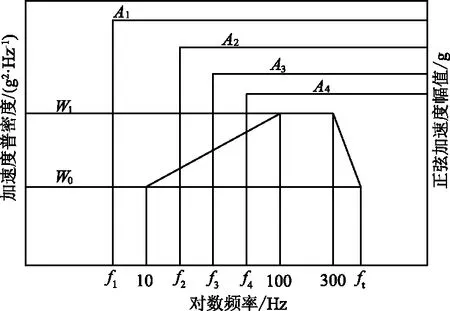
图1 直升机振动环境试验谱图Fig.1 Helicopter vibration environment test spectrum

图1中f1～f4为正弦四阶定频频率，A1～A4为对应的峰值加速度。根据试验要求，北斗设备安装位置为主桨影响区，对应的振动试验的量值如表1所示，可以发现f2=2f1，f3=3f1，f4=4f1。

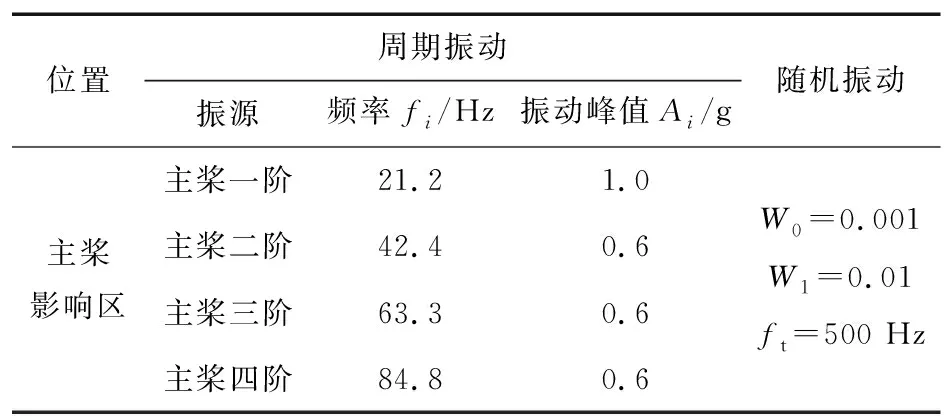
表1 振动试验量值

2 振动谱处理

北斗设备安装平台振动试验环境为宽带随机振动与定频正弦振动的叠加。Ansys有限元分析软件中的模态、谐响应、响应谱及随机振动等分析模块的输入条件无法直接处理这种组合谱的振动模式，环境试验谱无法直接同时施加在分析模型上。

文献[10]给出按照能量相等原则，将正弦定频振动转换为窄带随机振动，从而将宽带随机振动与正弦定频振动的叠加谱转换为窄带加宽带的纯随机振动，转换公式如下：

式中，GQ(f)为等效的窄带随机振动的功率谱密度；f为等效窄带带宽；A(fn)为正弦定频振动幅值；Q(fn)为品质因数，通过试验获得；fn为等效转换的正弦振动频率；β为等效因子，一般β=1.8。计算得到的各主要频点的功率谱密度值如表2所示。

表2 主要频点的功率谱密度值

根据表2绘制转换后的纯随机振动功率谱密度，如图2所示。

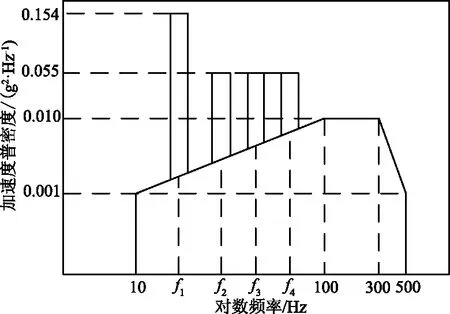
图2 等效随机振动功率谱Fig.2 Equivalent random vibration power spectrum

3 仿真分析3.1 北斗设备结构

按照《GJB 441-1988机载电子设备机箱、安装架的安装形式和基本尺寸》的要求，机载设备一般由安装架及设备主体组成。

本文研究的机载北斗设备具体形式如图3所示。其中安装架通过螺钉与机体进行连接，设备主体通过定位销轴与安装架进行定位后，使用前锁紧装置进行紧固。

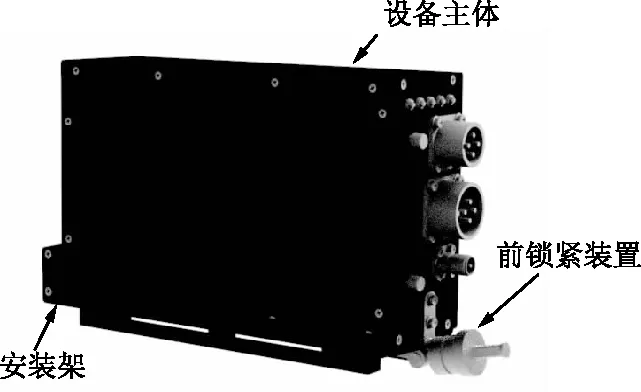
图3 机载北斗设备Fig.3 Airborne Bei-Dou equipment

安装架及设备主体均采用防锈铝合金5A06，密度为2 780 kg/m3，弹性模量73 Mpa，泊松比0.33，抗拉强度305 Mpa，屈服强度145 Mpa；前锁紧装置为不锈钢1Cr18Ni9Ti钝化，弹性模量194 Mpa，泊松比0.3，抗拉强度520 Mpa，屈服强度205 Mpa。

文献[11]规定设备振动摆动距离：设备垂直方向不得大于10.7 mm，水平方向不得大于25.4 mm。

3.2 有限元模型建立

仿真分析时需要对分析模型进行简化[12]，对结构中影响较小的零件、开孔及凸台等特征进行删除，简化后的分析模型如图4所示。

图4 设备有限元模型Fig.4 Equipment FEA model

3.3 模态分析

3.3.1 数学模型

文献[13]提出,N自由度线性系统的振动特性可由N阶矩阵线性定常微分方程描述，即：

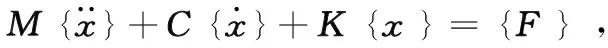
(1)

式中，M，K分别为系统的质量和刚度矩阵；C为系统的阻尼矩阵；{F}为外力向量，{x}为位移向量。

将线性定常系统振动微分方程组中的物理坐标变换为模态坐标从而实现方程组的解耦，变为以模态坐标及模态参数描述的独立方程，从而求出系统的模态参数。

模态坐标的表达式为：

(2)

式中，φ为固有阵型矩阵；{q(s)}为模态坐标向量。

将式(2)代入式(1)整理得模态坐标系下的振动方程为：

(Ki-ω2Mi+jωCi){q(ω)}=φT{Fi(ω)}，

其响应为：

模态计算时,模型内的每个单元都基于以上理论基础。

3.3.2 加载求解

在进行随机振动仿真分析前需要求出设备的模态，这是对结构进行解耦的必要前提条件。针对设备的安装形式对安装支架固定面进行自由度约束，使用Ansys软件中的modal模块进行模态分析求解，获得对应的固有频率及振型。

设备结构的前6阶固有频率如表3所示，一阶固有频率为718 Hz，比振动试验500 Hz高218 Hz，远离共振频率，不会发生共振，结构设计合理，可以直接用于振动试验。通过分析相应阶数下的阵型，如图5所示，得出设备结构主要变形及应力发生在左右横向方向。

表3 设备结构固有频率

图5 各频率对应的阵型

3.4 随机振动分析

根据试验要求，北斗设备需进行X，Y，Z三轴方向的随机振动，通过加载得出各方向的应力与位移响应，如图6所示。

图6 各方向应力与位移响应

3.5 强度校核

通过分析各方向应力与位移结果，得出如表4所示的响应数据。可以看出，在相同的随机振动激励下，北斗设备左右方向应力与位移响应为最大，与模态中的振型分析相吻合。

表4 各方向应力与位移响应值

最大von-Mises应力的3σ值为3.96 Mpa，远小于材料的许用应力145 Mpa；最大位移为1e-3 mm，远小于GJB 779-89中规定的25.4 mm，因此得出北斗设备结构设计满足直升机环境下的振动强度要求。

4 结束语

针对直升机振动环境具备的随机振动与正弦振动叠加的特点，提出采用能量相等原则，将正弦振动转换为窄带随机振动，与原有的宽带随机振动组合为纯随机振动谱。

将组合后的纯随机振动谱作为有限元分析软件Ansys的输入条件，对机载北斗设备进行模态及随机振动仿真分析，获得该振动谱下的应力与位移曲线，对强度及位移进行校核，为设备研制提供仿真依据。分析结果表明，结构强度满足使用要求，最终产品通过了鉴定试验，验证了仿真分析的可靠性。