一种基于代价函数的跳频周期估计算法
周德强,白雪飞,尤少钦,闫红超
(1. 河北省电磁频谱认知与管控重点实验室,河北 石家庄 050081;2.中国人民解放军32090部队,河北 秦皇岛 066000)
0 引言
跳频通信具有较强的抗多径、抗衰落、抗干扰和截获概率低等诸多优点,在军事通信领域获得广泛应用,因此对跳频信号的侦察成为通信对抗的主要领域之一。在跳频通信侦察中,跳频周期是一个重要参数,为了实现网台分选[1],需要对跳频周期进行精确估计。目前的跳频周期估计算法主要有3类:① 脉冲重复周期(Pulse Repetition Interval,PRI)[2-3]直方图类算法,包括CDIF算法、SDIF算法及其改进算法[4-5],这些算法也常用于雷达信号分选中;② PRI变换法及其改进算法[6-9],这些算法同样也常用于雷达信号分选中;③ 对跳频信号进行时频分析[10-13],提取跳频信号时频分布的峰值序列、时频脊线等特征[14-15],利用这些特征的周期性估计跳频周期[16-19]。PRI直方图类算法在跳频信号丢失率低并且跳频信号到达时间抖动很小的情况下估计效果较好。但在实际工程应用中,受限于时间分辨率,跳频信号的到达时间抖动很难控制到很小,在复杂电磁环境下跳频信号的丢失率也不能保证很低,因此PRI直方图类算法使用范围受限[4]。PRI类算法对到达时间进行PRI变换处理,通过在PRI谱图上搜索谱峰来估计跳频周期,该类算法在到达时间抖动较大时估计性能较差[7]。时频分析类算法通过提取跳频信号时频分布中的峰值序列、时频脊线等的周期来估计跳频周期,不能适应电磁环境中存在多网台的复杂情况[18-19]。
针对以上跳频周期估计算法中存在的问题,本文提出了一种基于代价函数的跳频周期估计算法,以相对到达时间的直方图统计的方差作为代价函数[20],代价函数最大值所对应的自变量即为跳频周期估计值。该算法不仅估计精度高,而且适应多网台存在的复杂电磁环境。
1 问题模型
对于通信侦察方,同一个电台发射的跳频信号的到达时间可以建模为一个等差数列,数列的公差是跳频周期。因此,第i个电台的第j跳信号的到达时间可以表示为:
ti,j=kiTi+toi+jTi,
(1)
式中,i=0,1,2,…;j=0,1,2,…;Ti是第i个电台的跳频周期;toi是取值范围为[0,Ti)的常量;ki是整数。跳频周期估计问题其实是已知跳频信号的一系列到达时间ti,j,求解跳频信号的跳频周期Ti。对于不同跳速的跳频信号,可以根据跳频信号的驻留时间将其区分开,因此跳频周期估计问题可以简化为:已知同一跳速的跳频信号的一系列到达时间ti,j,估计跳频周期T,其中ti,j可以表示为:
ti,j=kiT+toi+jT。
(2)
2 算法原理
假设未知的跳频周期为变量x,跳频信号的相对到达时间可以表示为:
(3)

构造代价函数:
(4)

(5)
对于非负实数a,b,有:
(a+b)2=a2+b2+2ab≥a2+b2。
(6)
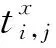

(7)
可见,此时每个网台的跳频信号的相对到达时间都变成了常量,分布的比较集中,直方图统计的方差最大,即代价函数J(x)最大。因此,跳频周期的估计值可以表示为:
(8)
式中,TL,TH是根据经验或者跳频周期粗估计算法确定的搜索范围的上、下限。
3 算法实现
本文采用搜索的方式实现基于代价函数的跳频周期估计算法,在[TL,TH]上以Δx为步长计算可能的跳频周期xk=TL+kΔx对应的代价函数值J(xk),最大函数值对应的自变量即为跳频周期的估计值,具体步骤如下:

情况 3 v9不染1, 不失一般性,假设它染3,则可用上述的方法将穷点v1,v5的颜色2改染为颜色1, 并用2 来染v。
② 根据式(3)和式(4)计算J(xk);

④ 更新k:k=k+1;
⑤ 计算xk:xk=TL+kΔx;
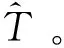
在实际实现中,可以采用变步长的搜索方法减少计算量[20]。
4 性能分析
(9)
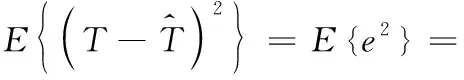
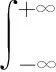
(10)
5 仿真试验
5.1 算法验证
算法中的搜索步长设置为1 μs,直方图统计的箱长设置为5 μs,搜索范围设置为900 ~1 100 μs。试验数据是在外场利用短时傅里叶变换检测到的3个电台的20 007跳信号的到达时间,短时傅里叶变换的时间分辨率为44.444 μs,3个电台的跳频周期均为1 ms,计算出的代价函数示意如图1所示。由图1可以看出,代价函数的最大值出现在1 ms处,该值等于跳频周期的真值,验证了算法的有效性。
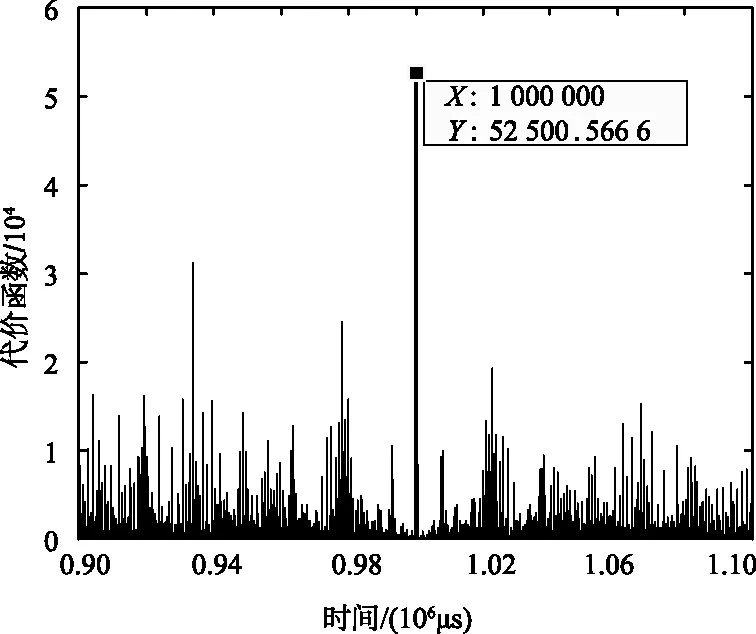
图1 代价函数示意Fig.1 Schematic diagram of cost function
5.2 搜索步长对算法性能的影响
本小节验证了搜索步长对算法性能的影响。在仿真中,搜索步长设置在1~19 μs之间,每种步长下进行1 000次蒙特卡罗仿真,每次处理3个1 000跳/秒的跳频电台的10 000跳信号。算法中直方图统计的箱长设置为5 μs,搜索范围是900~1 100 μs。仿真结果如图2所示。当搜索步长分别设置为1 μs和5 μs时,归一化均方误差其实是0,为了避免对0取对数,对所有的归一化均方误差都加了1×10-21。由图2可以看出,归一化均方误差并不是随着搜索步长的增加而严格增加的,这是因为当搜索步长和搜索范围的起始值设置的恰好合适时,即使搜索步长较大,也可能恰好搜索到真实的跳频周期,此时归一化均方误差较小。以本仿真为例,当搜索步长取5 μs时,900 μs+5 μs×20 = 1 000 μs,恰好能搜索到真实的跳频周期,归一化均方误差为0。当搜索步长取3 μs时,900 μs+3 μs×33 = 999 μs,900 μs + 3 μs×34=1 002 μs,可见此时不能搜索到真实的跳频周期,所以即使其搜索步长比5 μs小,但是归一化均方误差比5 μs时大。当跳频周期未知时,从统计角度上看,越小的搜索步长搜索到真实跳频周期的概率越大,归一化均方误差越小,因此在计算速度可容忍的情况下应该尽量减小搜索步长。

图2 不同搜索步长下的归一化均方误差Fig.2 Mean square error of normalized hopping cycle versus different search steps
5.3 丢跳适应性验证
考虑到在复杂电磁环境中存在丢跳情况,本小节验证了算法的丢跳适应性,并与文献[8]中的PRI变换法进行了对比。在仿真中,丢跳率设置在0~0.5之间只有一个500跳/秒的跳频电台,每种丢跳率下进行1 000次蒙特卡罗仿真,每次处理10 000跳信号。本文算法中的搜索步长设置为13 μs,直方图统计的箱长设置为5 μs,搜索范围是1 900~2 100 μs。PRI变换法的箱长设置为13 μs,搜索范围是1 900 ~2 100 μs。仿真结果如图3所示。由图3可以看出,本文算法和PRI变换法对丢跳率都不敏感,本文算法的性能略好于PRI变换法。
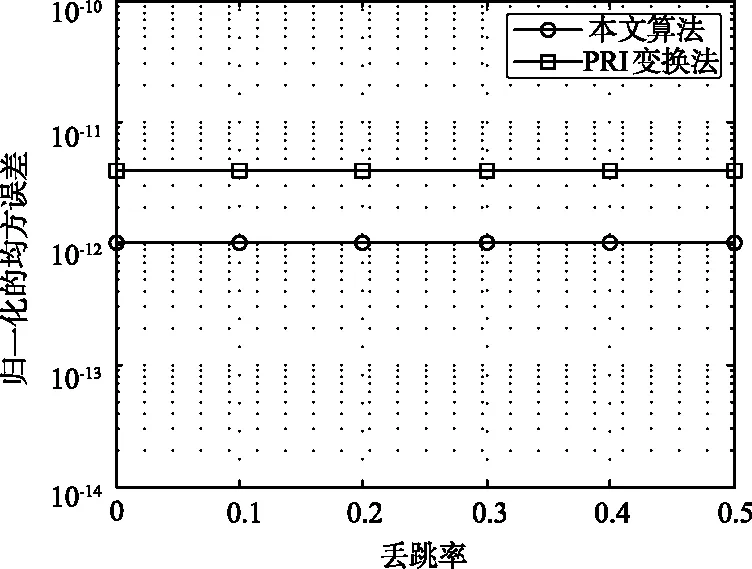
图3 不同丢跳率下的归一化均方误差Fig.3 Mean square error of normalized hopping cycle versus different data loss rates
6 结束语
本文提出了一种基于代价函数的跳频周期估计算法,从理论上推导了算法的合理性,利用外场数据验证了算法的正确性,通过仿真试验验证了搜索步长对算法的影响和算法对丢跳率的不敏感性。通过选择合适的搜索步长,跳频周期估计值的归一化均方误差可以达到0。本算法不仅估计精度高,而且鲁棒性强,对于网台分选的工程实现具有重要意义。

