快速求解粒球粗糙集约简的属性划分方法

巴 婧,陈 妍,杨习贝

(江苏科技大学 计算机学院,江苏 镇江 212100)

作为处理连续型和混合型等复杂数据的一种拓展粗糙集方法[1,2],胡清华等[3]提出的邻域粗糙集因其灵活的粒度表现形式,受到了众多研究学者的青睐。然而,在使用邻域粗糙集进行属性约简[4-6]这一问题的研究时,往往需要通过大量的尝试或采用一定的参数搜索策略来设置邻域半径的大小[7-9],这势必会带来极大的时间消耗。

为了克服邻域粗糙集中半径选取这一困难,已有相关学者借助自适应的理念,提出了一些能够自主确定半径大小的策略。例如,Zhou等[10]面向在线特征选择问题,提出了Gap邻域的概念,其使用样本间距离的差值确定邻域的大小,从而生成较为紧凑的Gap邻域粒结构;Xia等[11]为提升大规模数据中分类任务的效率,提出了粒球的概念,其过程是迭代使用2-means聚类,从数据自身的分布出发,生成大小不一的粒球,直至粒球的纯度达到预期目标。

粒球的纯度实际上是粒球中样本的标签与粒球标签相吻合的样本的比重,采用这一概念,Xia等[12]进一步地进行了基于粒球纯度的属性约简问题的研究。然而,若采用贪心搜索策略对基于粒球纯度的约简进行求解,依然会存在候选属性空间较大的问题,从而致使搜索效率不高。例如,采用后向贪心搜索时,对于每一个候选属性都要进行逐步的评估与尝试,以判断该属性是否可以被删除;而采用前向贪心搜索时,依然需要对每一个候选属性进行逐步的评估与尝试,以判断该属性是否可以被加入到约简集合中。

综上所述,如果从压缩候选属性数量的层面出发,基于粒球纯度的约简求解效率依然存在提升空间。因此,本文在前向贪心搜索约简的进程中,引入了属性划分策略。属性划分方法的本质是在搜索时,将所有属性划分成不同的组,从而以属性的分组为基准进行候选属性的筛选,仅评估那些与约简池中的属性不属于同一组的属性,以达到减少候选属性数量,提升约简求解效率的目的。其具体步骤为:(1)使用K-means方法对所有属性进行划分;(2)仅对所有未加入约简池且与约简池中任一属性不在同一划分中的侯选属性进行评估;(3)根据评估结果,挑选出最重要属性并将其加入到约简池中。这些步骤能够压缩候选属性的搜索空间,有望降低计算约简的时间消耗,实现约简的快速求解。本文所提出的基于粒球粗糙集的属性划分快速约简求解算法,不仅利用粒球粗糙集,从样本的角度对样本集进行分簇,而且通过引入属性划分的方法,从属性层面对约简过程进行加速。

1 基础知识

1.1 邻域粗糙集

(1)

式中:ΔA(xi,xj)表示依据条件属性集合A,样本xi与xj间的距离;δ为给定的半径。

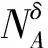
(2)

(3)

式中:Xp∈U/IND(d)表示具有相同标记的样本所构成的第p(1≤p≤n)个决策类。

1.2 粒球

邻域关系因其半径的存在,所以能够灵活地以不同的尺度刻画两个样本间是否相似。但在使用邻域时,半径的选择是一个难题。虽然目前可以采用诸如优化等方式挑选符合问题求解的合适的半径,但往往搜索效率较低。鉴于此,Xia等[11]依据数据自适应理念,提出了粒球的概念。与邻域不同的是,粒球能够根据数据自身的分布,自适应地刻画不同样本之间的相似性。在Xia等[11]的粒球理论中,粒球的结构主要包含两个指标:中心点以及半径。详细定义如下所示。

(4)

(5)

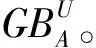
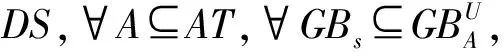
(6)

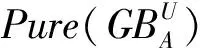
在Xia等[11]提出的粒球中,粒球的产生采用2-means算法,其主要步骤如下:

(1)将论域U视为一个类簇;

(2)利用2-means算法分别对每个类簇进行聚类;

(3)求得每一个类簇的中心点以及类簇中所有样本至中心点的平均距离;

(4)根据中心点及平均距离得到粒球,且求得粒球的纯度;

(5)遍历所有粒球,若粒球的纯度不低于给定阈值,则不再生成新的粒球,算法结束;否则返回步骤(2)。

1.3 粒球粗糙集

在求得粒球的基础上,Xia等[12]进一步提出了粒球粗糙集的概念如下所示。

GBs∩Xp≠∅}

(7)

(8)

1.4 属性约简

在使用粗糙集进行数据分析时,属性约简是一个关键科学问题。属性约简能够在某种给定的度量准则下,通过删除冗余或者不相关属性,以达到数据降维及提升学习器性能的目的,近年来受到了诸多学者的广泛关注。一般来说,属性约简的形式化定义如下所示。

(1)Abs(ε(A)-ε(AT))≤ζ;

式中:Abs(ε(A)-ε(AT))表示根据不同属性集合所得到的度量值之差的绝对值,ζ表示对给定度量的包容度。

包容度ζ的设置会使得约简条件不必过于严苛,文中取值设置为0.95。因此,在定义7中,条件(1)保证相较于原有属性集合,所选择出的属性子集在给定的度量上不会带来较大的偏差;条件(2)保证所选择出的属性子集中没有冗余属性的存在。

在很多已有的研究成果中,ε可采用近似质量(下近似集中样本占所有样本的比重)进行计算;在粒球粗糙集方法中,Xia等[12]则采用粒球中独有的纯度作为ε的计算方式。

2 基于粒球粗糙集的约简快速算法

2.1 后向贪心约简求解

在粒球粗糙集理论中,Xia等[12]以粒球的纯度为度量标准,不仅给出了相应的属性约简概念,而且利用后向贪心删除策略,设计了求解约简的算法,具体描述如算法1所示。

算法1基于粒球粗糙集的后向贪心约简求解算法

输入:决策系统DS=〈U,AT∪{d}〉;

输出:red;

步骤1初始化,令red=AT;

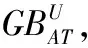
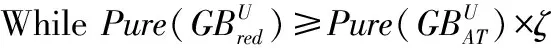
(3)red=red-{b};

End

red=red∪{b};

End

步骤5输出red。

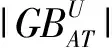
2.2 前向贪心约简求解

在利用贪心策略求解约简这一问题中,Yao等[14]将贪心搜索划分为两大类:减法控制策略和加法控制策略。实际上,算法1所描述的后向贪心算法体现了减法控制策略的基本思想。为进一步丰富粒球粗糙集中属性约简问题的研究,算法2将根据加法控制策略的基本思想,设计出前向贪心搜索算法以求解约简。

算法2基于粒球粗糙集的前向贪心约简求解算法

输入:决策系统DS=〈U,AT∪{d}〉;

输出:red;

步骤1初始化,令red=∅;

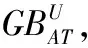
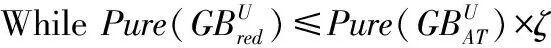
(3)red=red∪{b};

End

步骤4输出red。

2.3 基于属性划分的约简快速求解

根据2.1和2.2节,不难发现算法1和算法2的时间复杂度相同。由于算法1和算法2的时间消耗均极大地依赖于粒球的个数,而粒球的个数又极大地依赖于数据本身的分布,故当粒球个数较多时,对每个粒球进行遍历以求解平均纯度,会致使约简求解的时间消耗较高。鉴于此,下文将提出一种新的约简求解策略,即基于属性划分的粒球约简求解方法。

在属性划分方法中,优先选取对提高平均纯度有较大帮助的属性且这些属性需与约简池中的属性具有较高的不相似度,这样可以在一定程度上压缩候选属性的搜索空间,以达到减少时间消耗的目的。此处采用K-means聚类的方法来判定两个属性之间是否具有较高的不相似度,若两属性处于不同划分中,则认为这两个属性间的不相似度较高。基于上述思想,算法3构建了一个基于粒球粗糙集的属性划分快速约简求解算法,该算法在对全部属性集合进行划分后,将侯选属性中与已在约简池中属性属于不同划分的属性加入到约简集合中,直至满足约简所需约束。

算法3基于粒球粗糙集的属性划分快速约简求解算法

输入:决策系统DS=〈U,AT∪{d}〉;

输出:red;

步骤1利用K-means聚类算法对属性集合AT进行分组,以求得属性划分;

步骤2初始化,令red=∅,T′=∅;

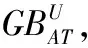
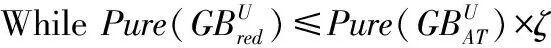
(1)令T=AT-red;

(3)若T=∅,转(4),否则转(5);

(4)T=AT-red,T′=∅;

(5)在T中找到属性b,使得b=

(6)red=red∪{b},T′=T′∪{b};

End

步骤5输出red。

为了便于理解本文所提算法的主要原理,以下给出一个简单的示例。

例1对于表1所示的决策系统DS=〈U,AT∪{d}〉,其中U={x1,x2,x3,x4},AT={a1,a2,a3,a4}。

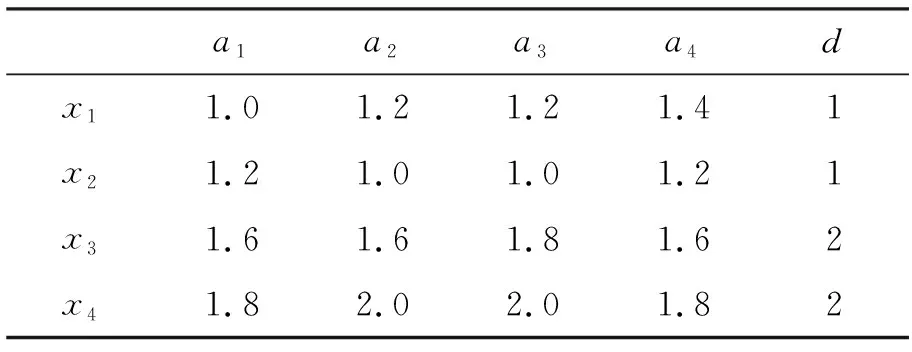
表1 决策系统示例

根据算法3所示步骤,具体计算过程如下所示:

(1)利用K-means聚类算法对属性集合AT进行分组,得到属性划分为{a1,a2}和{a3,a4};

(2)将属性a1加入到约简集合中,计算得到在约简集合下粒球纯度为1,即red=red∪{a1};

(3)由于属性a2与a1在同一属性划分中,故将a3加入到约简集合中,计算得到在约简集合下粒球纯度为1,即red=red∪{a3};

(4)循环步骤(2)和步骤(3),直至满足约简条件。

3 实验分析

为了测试所提算法的有效性,本节进行了相关的实验对比。所有实验均采用MATLAB R2018a实现,操作系统为Windows 10,CPU为Intel®Core(TM)i5-4210U,内存为8.00 GB。本节实验从UCI标准数据集中选取了10组数据,这些数据的基本信息如表2所示。

表2 数据集描述

本节实验除了实现文中所示的算法1、算法2和算法3外,还将这些算法与基于邻域粗糙集的前向贪心约简求解方法(简称邻域)进行了比对。由于邻域粗糙集涉及半径选取的问题,故本组实验以步长为0.02,选取了0.02、0.04、…、0.40等20个不同半径,并在这20个不同半径下,求取进行约简求解所需时间消耗的均值。需注意,上述所示的4种算法均采用十折交叉验证进行测试。

此外,通过大量的前期测试,对于算法3所涉及的K-means聚类,笔者发现K取值为「|AT|/3⎤时,可以使得所提算法展现出较好的性能。

3.1 时间消耗比对

在本组实验中,对算法1、算法2、算法3和邻域粗糙集约简求解的时间消耗进行统计,具体时间消耗如表3所示。

表3 不同算法求解约简的时间消耗对比 s

观察表3,不难得出以下结论。

(1)利用邻域粗糙集求解约简,其所需要的时间远超过算法1和2所需的时间,说明在使用粒球粗糙集进行约简求解时,能够大大提高约简求解的效率。以数据Breast cancer wisconsin(Diagnostic)为例,在利用邻域粗糙集求解约简时,平均时间消耗为3.011 0 s时,而算法1和2所需的时间分别为0.068 3 s和0.014 4 s。由此可见,相较于基于邻域粗糙集的约简求解,基于粒球粗糙集的算法1和算法2,效率较高。

(2)相较于算法1和2,算法3所需的时间消耗较低,说明从属性间相似度出发,将属性进行划分并求取约简,确实能够进一步地降低所需的时间。以数据Ionosphere为例,算法1和2所消耗的时间分别为0.453 6 s和0.435 7 s,而算法3所消耗的时间仅为0.329 3 s。由此可知,引入属性划分方法后确实能够加速约简求解的进程。

表4进一步地展现了不同算法之间的加速比,其中,加速比为相应的对比算法所需时间与所提的算法3所需时间的比值。观察表4,可以清晰地发现相较于邻域粗糙集的约简求解、算法1和算法2,算法3能够提供较好的加速比,从而进一步地展现了算法3在时间效率上的优越性。

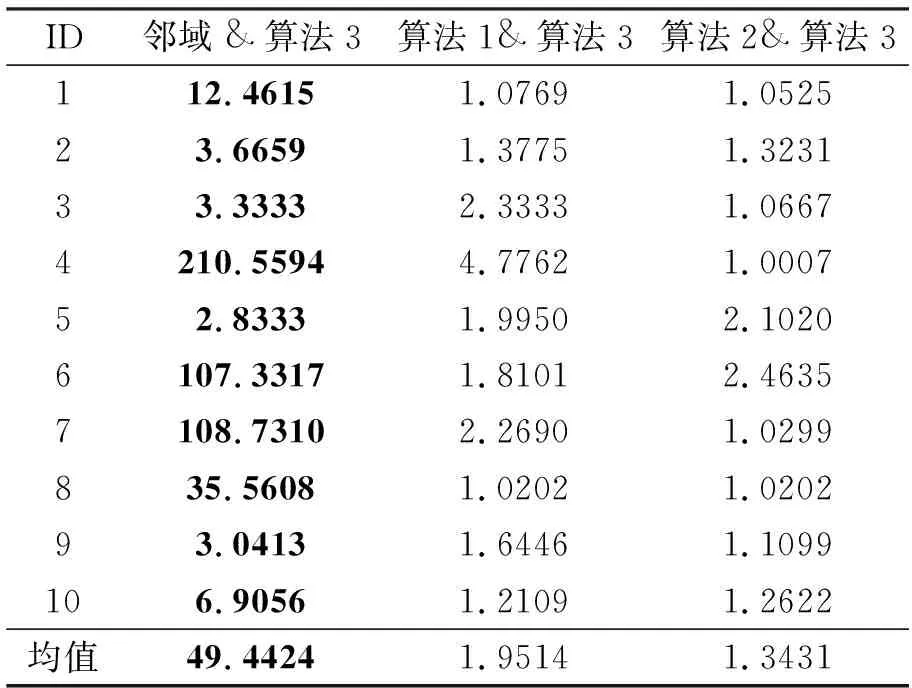
表4 求解约简所需时间的加速比

3.2 分类准确率对比

在本组实验中,采用K最邻近(K-nearest neighbor,KNN;K=3)和支持向量机(Support vector machine,SVM)(libSVM默认参数)两种分类器,对约简的分类性能进行展示。表5展现了不同算法所求得的约简在测试集上所得到的分类准确率的均值。

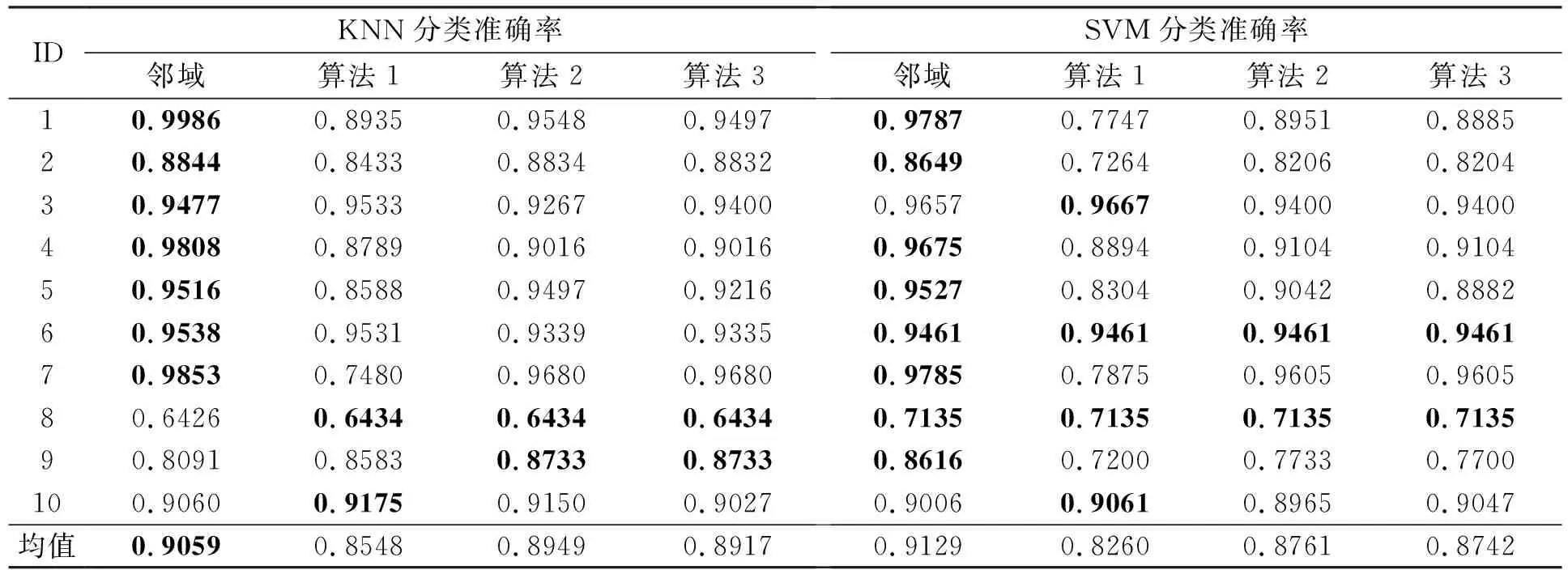
表5 KNN和 SVM 分类器的分类准确率

观察表5,不难发现无论是采用KNN还是SVM分类器,利用4种算法求得约简在分类性能上相差不大,这说明基于粒球粗糙集的属性划分约简算法能够产生较为满意的约简。但综合考虑时间消耗,算法1和2的时间消耗低于邻域粗糙集约简求解的时间消耗,算法3的时间消耗又低于算法1和2的时间消耗。可见,基于粒球粗糙集的属性划分快速约简求解算法不仅能够减少约简求解的时间,而且相较于其他算法来说,也能够提供具有相当分类能力的约简。

4 结束语

为了降低利用贪心搜索算法求解约简所带来的时间消耗,本文在粒球粗糙集的基础上,利用属性间的相似度对属性进行划分,从而能够切实减少约简进程中在属性搜寻层面上的时间消耗。实验结果验证了所提算法的有效性。在此基础上,今后将就以下问题进行深入探索:

(1)所提属性划分方法实际上是在属性层面上针对快速约简问题进行了探讨,今后可以进一步地同时从属性和样本两个层面对快速约简问题进行研究;

(2)除了采用粒球的纯度以外,还可以采用诸如粒球的生成正域、条件熵[15]等度量对粒球粗糙集的属性约简问题进行深入研究。