基于压电陶瓷的不同服役年限木构件损伤监测*

蒙卉恩杨 霞李顺涛杨文伟*

(1.宁夏大学土木与水利工程学院，宁夏 银川750021；2.宁夏土木工程防震减灾工程技术研究中心，宁夏 银川750021；

3.湖南大学土木工程学院，湖南 长沙410082)

木结构建筑具有韧性好、抗震性强、施工周期短和节能低碳等优点，因此在全球有着悠久的使用历史，同时在现代建筑中仍占有较重的使用比例。 但木结构建筑在建设或使用过程中会因自然或人为因素产生腐朽、虫蛀、裂缝、拔榫等问题，因此，对已有或正在建设中的木结构建筑进行健康监测与损伤诊断，或在灾害发生后对建筑结构进行损伤评估及剩余寿命预测具有重要意义。

随着结构健康监测技术和损伤诊断技术的快速发展，一些常规的损伤监测技术已经在木材和木结构上得到了应用，如超声波[1-2]、模态参数[3-5]、软电容[6]和电阻法[7-8]等监测技术。 但这些方法在木结构的健康检测中仍存在着诸多不足和使用限制。 本文所采用的压电陶瓷，因其反应速度快，频响范围广，易剪裁，成本低，在工程结构的健康监测方面有巨大的应用潜力。 从20 世纪90 年代起，基于压电陶瓷的损伤监测技术在金属和混凝土等材料的健康监测中得到了广泛的应用[9-11]，近年来其技术也逐渐应用在竹木结构健康监测领域，如，Zhang 等[12-13]将压电陶瓷片粘贴在木材表面，对木材人工模拟状态下的损伤及含水率进行了识别，试验结果表明，基于压电陶瓷的主动监测方法可以较好的识别木材的损伤及含水率的变化。 同样，Dansheng 等[14]基于机电阻抗技术监测木材的损伤，提出基于均方根偏差(RMSD)的损伤指数来评价木材试件的损伤程度。 马晓倩等[15]利用应力波对竹梁界面剥离进行监测。 试验结果表明，该方法可对竹梁试件在加载过程中界面剥离损伤状态进行有效监测。 Han 等[16]和Zhao等[17]采用基于压电陶瓷的主动监测技术对木试件连接状态进行监测，试验结果表明，随着连接损坏程度的增加，接收到的信号能量随之衰减。 王浩[18]和王清华[19]将压电阻抗技术应用于木试件损伤检测及木梁损伤定位中，研究表明，该技术对木试件损伤监测敏感，具有木梁损伤定位能力。刘孝禹等[20]基于压电传感器对木试件在轴压作用下进行损伤监测，结果表明，信号的幅值能很好的反映木材的损伤程度。

虽已有许多学者开展了基于压电陶瓷的竹木结构健康监测及损伤识别研究，但是对不同服役年限木材的损伤识别研究还鲜有报道。 基于此，本文利用基于压电陶瓷的主动传感方法对不同服役年限的木材进行试验研究，将服役年限不同的木材制作成尺寸相同的试件，在试件的六个面上分别粘贴压电陶瓷片，作为驱动器及接受器用于信号的发射及接收。 通过对比三个试件相应监测方向上信号的幅值、小波包能量及功率谱密度的差异，验证了该方法的有效性，以及信号幅值对不同服役年限木材损伤监测敏感，可为实际工程中不同服役年限木结构建筑的监测识别提供一种新的思路。

1 基本原理

1.1 压电效应

压电材料具有压电效应这一项重要特性[21]，当对压电材料进行挤压或拉伸时，材料两端产生符号相反的电荷，这种将机械能转化为电能的现象称为正压电效应，反之，当对压电材料施加激励电场时，材料产生机械变形，这种将电能转化为机械能的现象称为逆压电效应。

压电陶瓷用于结构健康监测中时可采取表面粘贴式和内部嵌入式两种，为了减少对木结构本身的破坏，本文利用AB 胶将压电陶瓷片粘贴在试件表面，对木结构试件进行健康监测。 本试验选用深圳市芙蓉电声科技有限公司生产的型号为FR 15 mm TL-10.5K 型压电陶瓷传感器元件作为驱动器和传感器，如图1 所示，元件尺寸为直径15 mm。

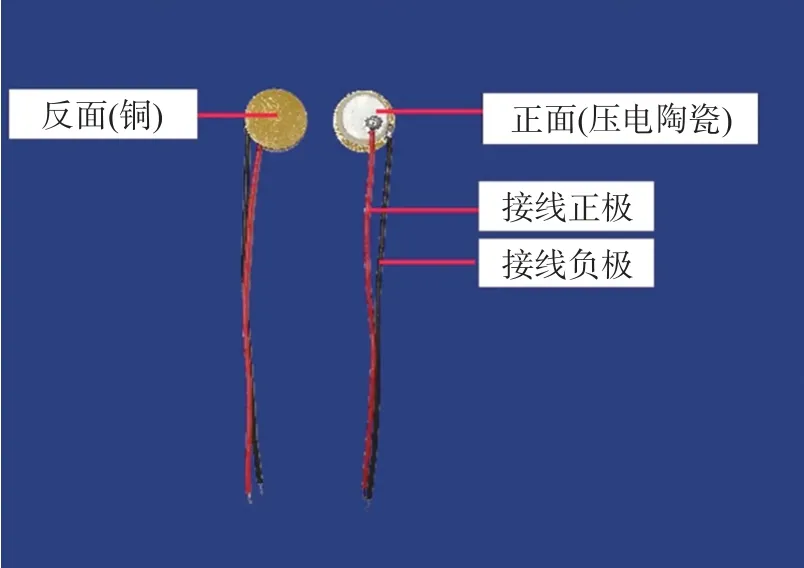
图1 传感器元件

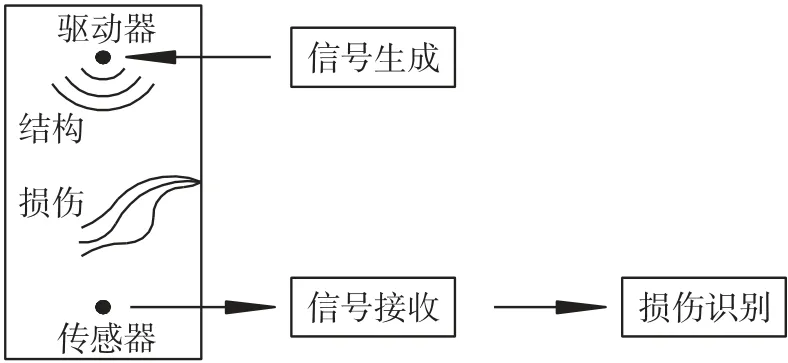
图2 基于波传播法的结构损伤监测原理

1.2 波传播分析法

基于压电陶瓷的主动传感技术主要包括波传播分析法和机械阻抗法两种[22]。 本文运用波传播分析法，其监测原理是将压电驱动器、压电传感器及木试件组成一个智能监测系统如图2 所示。 文中首先将粘贴在试件表面一端的PZT 作为驱动器，当外部电场激励作用时，驱动器发射扫频电信号，由于压电陶瓷的逆压电效应，被激励的压电驱动器产生高频应力波以木结构试件为介质进行传播，位于试件另一端的PZT 将接收高频应力波并转化为电信号输出。 应力波在传播过程中受结构含水率、裂缝、孔洞等因素影响发生反射、衍射及透射等现象，引起压电传感器接收到的信号的幅值衰减、能量减弱及传播时间延迟等。 通过分析不同服役年限木试件所接收信号的差异来识别结构存在的损伤及缺陷。

1.3 小波包分析法

小波包分析在信号处理、图像处理、量子力学等领域有着广泛的应用。 在傅里叶分析及小波分解基础上小波包变换[23]得到了发展，它克服了傅里叶分析处理非平稳信号时的局限性，解决了短傅里叶变换窗口大小恒定、分辨率固定的问题，优化了小波分解只对低频信号进行再分解的缺点。 小波包分解将信号分成不同频段，根据被分析信号的特性，选择合适的频带，对高频信号及低频信号均进行分解，这种分解无疏漏、无冗余，达到细化信号的效果，因此在工程损伤监测中具有广泛的应用价值。 小波包分解示意图如图3 所示，具体分解步骤如下。

图3 三层小波包分解

使用小波包分析将原始监测信号S分解为由多个尺度相同的频带组成的信号。 原始监测信号经过N层小波包分解且重构后可得到2N个子信号Si(i＝1，2，…，2N)，则:

将特征信号经过小波包分解后所得末层信号中各频带子信号的能量向量定义为[24]:

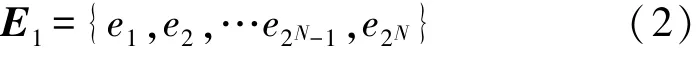
式中:ei为末层的各频带子信号能量，且:

则信号S经小波包分解重构后所得的总能量为:

基于小波包分解重构的小波包能量与原始监测信号的能量等价，因此可利用小波包能量表征原始监测信号的能量。 本文通过选取db3 小波函数，对原始信号进行五层分解，得到不同服役年限木材中信号的小波包能量。

1.4 功率谱密度分析法

功率谱密度谱分析[25]是一种概率统计方法，实现了信号的时间域向频率域的转化，属于结构的频域分析。 将有限长序列x(n)(0≤n≤Ns-1)按段长为M进行分段，段与段之间的重叠量为M-K，经加窗后第i个数据段表示为xi(n)＝G(n)x(n＋iK)(0≤i≤L-1，0≤n≤M-1)，K为整数，L为分段数，它们之间满足关系(L-1)K＋M≤Ns，G(n)为窗口函数，可以得到该数据段的功率谱密度为

式中:U为归一化系数，为了保证得到的功率谱是真正功率谱的渐近无偏估计而使用归一化系数。 由此可得平均功率谱值为:

功率是信号的重要属性，其功率谱图直接反映信号在频域中频率所对应的功率谱密度值，能很好体现信号变化的局部细节特征，可为结构缺陷诊断提供量化指标。

2 试验研究

2.1 材料性能

试验中的木材均为杉木，分别取服役年限为0年、3 年和40 年的杉木用于试验研究，如图4 所示。其中，使用服役为0 年的木材为新木材，还未被使用于结构中，使用年限为3 年和40 年的木材均取自贵州东南部某一苗寨里居民们所居住过的吊脚楼枋穿柱部位。

图4 不同服役年限木材

2.2 试件设计与制作

为研究不同服役年限木材的损伤程度，取服役年限分别为0 年、3 年、40 年的木材取心材部位制成3个试件，分别命名为试件1、试件2、试件3，3 个试件尺寸均为100 mm×50 mm×50 mm，对于每个试件，使用AB 胶将3 对压电陶瓷片粘贴在预定位置，用于信号的发射与接收。 考虑木材含水率对信号的影响，本研究采用国家标准(GB/T 1931—2009)，将试件置于烤箱中，在(103±2)℃的温度下烘烤8 h，取出称量，随之每2 h 称量试件一次，当最后两次称量质量之差不超过试件质量的0.5%，则认为试件已全干，按此方法将试件均烤至全干，试件实物图如图5 所示。

图5 木结构试件

文中将试件平面尺寸为100 mm×50 mm 且沿木材弦向生长的平面编号为A，平面尺寸为100 mm×50 mm 沿木材径向生长的平面编号为B，平面尺寸为50 mm×50 mm 沿木材纵向生长的平面编号为C。试件1 粘贴的PZT 驱动器编号为P ＋平面编号＋1，此平面对应的平面粘贴的PZT 传感器编号为P＋平面编号＋2。 相应的试件2 粘贴的PZT 压电陶瓷片编号为S＋平面编号＋1(2)，试件3 粘贴的PZT 压电陶瓷片编号为D＋平面编号＋1(2)，三个试件粘贴的压电陶瓷片具体编号见表1。 试件1 粘贴的压电陶瓷片预定位置如图6 所示，试件2 与试件3 与其相同。 为保证试验数据的准确性，3 个试件除使用年限不同外均无孔洞、裂缝等明显缺陷，信号采集在相同试验条件下完成。

图6 压电陶瓷片粘贴位置

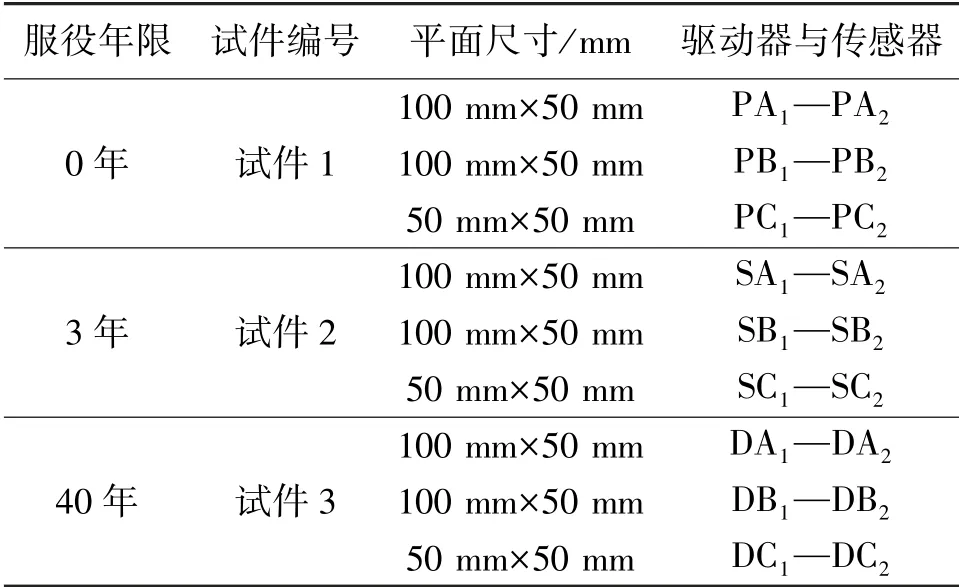
表1 PZT 压电陶瓷片编号详情

2.3 数据采集

试验时，采用江苏三川智能科技有限公司生产的多功能压电信号监测与分析系统，此系统集信号发生器和示波器于一身，可同时进行信号生成与信号采集。 根据波传播分析法的基本原理，木结构试件上的驱动器与模拟信号通道口连接，传感器连接到信号接收口，电脑终端连接到其他通道口，并通过与之配套的SCHYPZTV3 软件对数据进行采集、存储。 图7 为监测系统实物图。

图7 监测系统实物图

本次试验均采用一次激励一次接收的形式进行，在每次测试中，执行主动监测方法，试件两端的PZT 分别作为驱动器及传感器用于信号的发射及接收。 监测信号选取扫频正弦波，由于每种材料对信号的频响范围不同，因此为了确定杉木结构的频响范围，在正式试验之前，需进行多次预实验，即通不断调整扫频范围，观察采集到的信号的时域波形，寻找信号幅值较大的时间段，根据扫频时长推算出该时间段的大致扫频范围，最后依照推算出的扫频范围再次激励试件。 该过程重复进行，直到确定本试验中所用试件的扫频范围。 按以上方法，确定其扫频范围为20 kHz ～270 kHz。 试验中扫频正弦波信号的扫频时长为250.5 ms。

监测系统在工作过程中，信号会受外部工作环境，如温度湿度变化、电流电压波动以及一些工作中的电子设备等因素影响。 为了减少这些外部因素的干扰，采集过程中均进行了实时滤波，滤波拓朴结构采用巴特沃斯、带通、阶数为5，滤波范围为30 ～250 kHz。 同时，为了避免随机误差造成试验结果具有不确定性，在每次测试中进行多次激励，直到信号波形平稳再将数据保存并导出。 扫频正弦波信号的试验参数及滤波参数如表2 所示。

表2 试验参数

3 试验结果分析

3.1 基于信号幅值的结果分析

3 个试件在不同监测方向上的时域信号分别如图8 ～图10 所示，从采集到的PZT 信号输出波形来看，在木结构试件A 面和B 面上(即试件的弦向和径向)，均呈现出服役年限为0 年的试件的信号幅值最大，服役年限为3 年的次之，服役年限为40 年的信号幅值最小的变化规律。 由于木结构在使用过程中出现老化，木材中纤维素、木质素的改变使木材各项指标有不同程度的变化进而影响应力波的传播，因此信号幅值的这种衰减是可预测的。 一个有趣的发现是:在木结构试件C 面上(即试件的纵向)，服役年限为40 年的试件的信号幅值最大，3 年的次之，服役年限为0 年的试件信号幅值最小，这与A 面及B 面上信号的变化规律完全相反，这是由于木材属于各向异性材料，旧杉木相较于新杉木，其主要是表面和端部腐朽，内部空隙少，且新杉木沿纵向的干裂缝隙较多，这直接影响了应力波的传播。 由各个面上信号幅值的变化规律可以初步说明该监测方法可有效识别不同服役年限的木材。

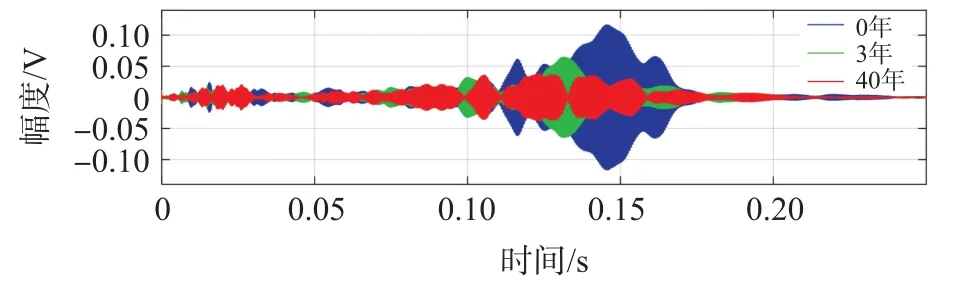
图8 A 面上PZT 传感器接收信号的幅值

图9 B 面上PZT 传感器输出的信号的幅值

图10 C 面上PZT 传感器输出的信号的幅值

3.2 基于小波包能量的结果分析

为了进一步验证所提出方法的可靠性，运用小波包分析方法，计算不同服役年限木材不同监测方向上信号的小波包能量如图11～图13 所示。

图11 A 面小波能量对比

图12 B 面小波能量对比

图13 C 面小波能量对比

由图11 和图12 可以观察到，在木结构试件A面和B 面，服役年限为0 年的试件的小波包能量最大，服役年限为3 年的试件的小波包能量次之，服役年限为40 年的试件的小波包能量最小。 由图13 可以看出，在木结构试件C 面，相较于服役年限短的试件，长年限试件的小波包能量更大。 此外B 面和C 面能量值较大，A 面较小。

为了更加直观的看到不同监测方向上信号的小波包能量的变化规律，表3 给出了小波包能量的具体数值及同一监测方向上其他服役年限的试件相较于服役年限为0 年的试件的能量值变化率。 由表3观察到A 面和B 面上服役年限为3 年和40 年的试件的能量值变化率均为负值，C 面上的试件的能量值变化率为正值。 其中A 面上服役年限为3 年和40年的试件的能量值变化率分别为- 78.03% 和-81.84%，B 面上服役年限为3 年和40 年的试件的能量值变化率分别为-83.54%和-85.21%，A 面和B面上能量值变化率的数值较为接近，且随木材服役年限的增加，能量值变化率小幅度增加。 C 面上服役年限为3 年和40 年的试件的能量值变化率分别为82.72%和517.81%，40 年的试件的能量值变化率是3 年的6.2 倍左右，其能量值变化率较A 面和B面增加幅度较大。

表3 信号的能量值及能量值变化率

3.3 基于功率谱密度的结果分析

笔者计算了3 个试件不同监测方向上的功率谱密度，并绘制了功率谱密度随频率的变化曲线(见图14)。

图14 监测信号的频域图

由图14 可知，在试件A 面上及B 面上，随木结构试件服役年限的增加，采集信号功率谱的值随之减小。 与A 面和B 面不同，在C 面上，随木结构试件服役年限的增加，采集信号功率谱的值随之增大。此外，每个监测方向上不同服役年限的木结构试件的固有频率不相同，随着服役年限的变化也没有明显规律，这是因为树木的生长是周期性的，有生长期和休眠期，所以木材是非均质的，则采集信号的固有频率也不相同。 同时同一块试件不同监测方向上的功率谱密度值相差较大，这是由于木材属于各向异性材料，每个生长方向微观结构存在差异。 木结构试件的A 面及B 面均属于树木的横向，所以随着试件服役年限的增加，采集信号功率谱的值的变化规律大致相同，而C 面属于树木的纵向，采集信号功率谱的值的变化规律则和A 面及B 面相反，三面的功率谱密度变化规律与信号的幅值变化规律相符。由此发现，信号的功率谱密度也可以作为识别木材的服役年限的一个指标，通过与已知服役年限的木材对比判定未知服役年限的木材的大致服役年限。

4 结论

①本文提出的基于PZT 的监测方法和基于小波包能量的损伤评估方法可以实现对不同服役年限的木结构试件的监测识别。 信号的幅值、小波包能量及功率谱密度这三个指标对基于压电陶瓷的不同服役年限的木结构监测识别表现出较好的敏感性。

②对试验中PZT 传感器输出的信号幅值及小波包能量的分析结果表明，在木材径向和弦向上随着木材服役年限的增长，接收信号的幅值及小波包能量均随之减小，而在木材纵向上随着木材服役年限的增长，接收信号的幅值及小波包能量随之增大。木材横向和纵向采集信号的幅值及能量呈现出完全相反的变化规律，这主要与木材的各向异性有关。

③计算信号的功率谱密度，发现在木材的径向和弦向上随着木材服役年限的增加，采集信号的功率谱密度随之减小，且变化明显，在木材纵向上信号功率谱变化规律与横向的变化规律相反，即随着木材服役年限的增加，监测信号的功率谱密度随之增加，由此说明信号的功率谱密度也可以作为判定木材服役年限的一个指标。