弹性支承索力参数精度识别方法的研究

李志亮

（中交第四公路工程局有限公司，北京市 100020）

0 引 言

索力对于索桥梁结构至关重要，是桥梁主体最重要的承重结构。在实际工程施工中，索力的控制测量是技术中比较重要的一个环节，只有通过准确测量拉索索力值才能更好地控制工程质量[1]。在桥梁运营过程中，索在复杂外界环境作用下容易产生腐蚀、振动损害，这些损害将直接导致拉索的索力下降，而拉索作为承受桥梁荷载的主要构件，索力的下降会直接影响桥梁行车的安全，使桥梁使用寿命和使用功能受到严重影响。所以，在桥梁施工过程中和使用过程中需要实时监测索力的变化情况[2]。

1 拉索索力常用测量方法及分析方法

1.1 索力常用测量方法

现阶段常用于索力测量的方法有压力表测值法、压力传感器测量法、电磁测量法、振动频率测量法和模态参数识别法。压力表测值法和压力传感器测量法一般只能在施工阶段使用，且设备较重，测量需要人力物力较多，成本较高，测试工作需要较长时间才能完成；电磁测量法在施工和运营阶段都可以用于测量，由于所需仪器设备较重，测量成本高，一般不适用；振动频率测量法可以用于施工和桥梁运营阶段，但是对于边界条件比较复杂的情况，无法精确识别索的固有频率，致使误差较大；模态参数识别法是根据拉索的等效长度，通过索力的固有振动频率特性来识别计算推导出索的索力和抗弯刚度，此方法成本低，精准识别程度高[3]。

1.2 索力分析方法

1.2.1 能量平衡分析索力

拱桥吊杆索力可以不考虑剪切变形和转动惯性量对索力的影响，因为吊杆截面净直径与计算的索长比值较小，剪切变形和转动惯量可以忽略。一般拱桥的吊杆都使用等截面拉索，索的抗弯刚度和质量在索上均匀分布[4]。图1 为索动力分析模型。

图1 索动力分析模型

在抗弯刚度影响下，索平面竖向振动平衡计算方程为：

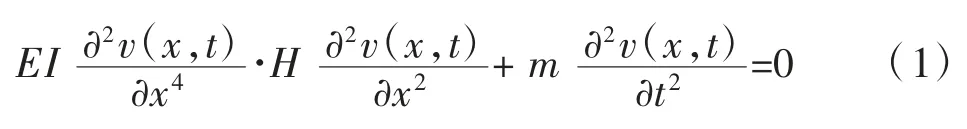
式中：EI 为索的抗弯刚度；v（x，t）为由于振动产生的竖向振动；H 为索力的水平分量；x 为距左端边界的距离；m 为单位长度索的质量。

如果假设吊杆横向位移量是由振幅随时间t 变化的固定形状来确定的，那么吊杆的横向位移可表示为：

式中：φ（x）为由边界条件决定的形状函数；ω 为吊杆的固有圆频率，ω=2πf，f 为吊杆的固有频率；θ 为相位角。

令最大动能和最大势能相等，则：

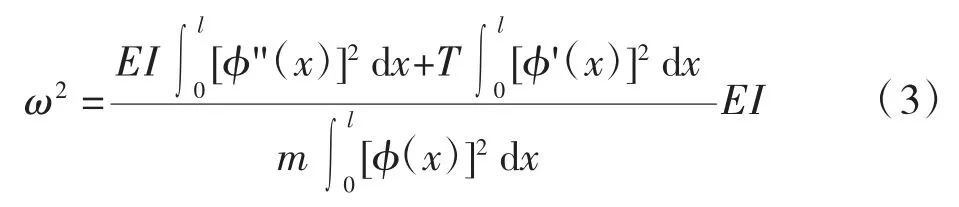
由式（3）中索力T、索的抗弯刚度EI、吊杆的固有圆频率ω 三者的关系，可进一步推导出相关函数的相应图形模型，从而计算求得各关系式中各个积分项的值，进而求得索力T 的显式表达式。

1.2.2 边界约束识别

桥梁索振动模态的节点取决于索无量纲参数ζ以及索两端弹性嵌固刚度k1和k2的大小。对于某一模态，对桥梁边界条件影响较大的位置是距离支座最近的节点和支座间的距离。若测量点与支座间的距离为d，由吊索自由振动的反应谱可以推断判别出第n 阶模态的节点。

2 索力测量和索力计算

2.1 索力计算方法

索力计算是通过软件系统程序测量索的振动频率，再通过振动频率绘制频率和索力的相关性，得到索力随时间变化的曲线，从而确定桥梁索的健康状况。

根据索的振动频率可以计算索力的大小。计算时，可以选择振动前3 阶中较大的1 阶频率进行计算，也可以同时考虑多阶频率进行综合计算。

如果以两端固定为索力的边界条件时，索力T的理论计算公式为：

式中：m 为索的单位长度质量，kg/m；l 为索长，m；f1为基频（索的第1 阶振动频率），Hz。

如果采用固定两端张紧的弦来模拟斜拉索，索力T 的理论计算公式为：

式中：n 为频率阶数；fn为索的第n 阶自振频率，Hz。

2.2 索力与频率的相关性分析

一般情况下，相关性分析用于研究2 个确定信号之间的相关性，通常采用自相关分析和互相关分析 2 种分析方法[5]。

用于描述自相关函数信号x（t）在2 个时刻之间取值相关关系的计算公式为：

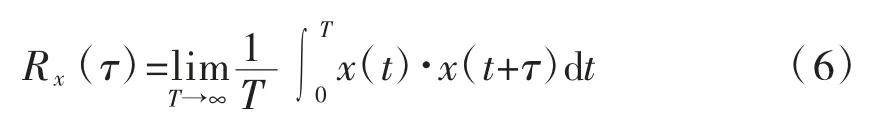
式中：Rx（τ）为相关函数；x（t）为要分析的信号序列；τ 为延迟时间。

对 2 个信号 x（t）和 y（t）进行相关分析时，采用的是互相关函数，该函数Rxy（τ）用来描述x（t）在某一个时刻的取值与y（t）在另一个时刻取值之间的依赖关系，可以表示为：

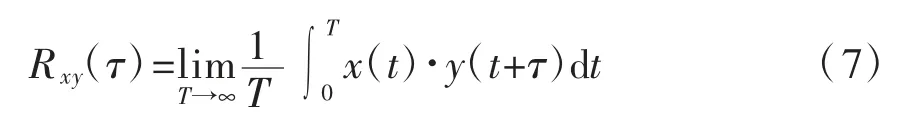
2.3 索力模态参数识别法在工程实例中的应用

2.3.1 以斜拉桥索力为例

以内蒙古某桥斜拉索测得的试验数据为例，索力的单位长度质量为1.11 kg/m，用m 表示；索长为2 112 m，用l 表示；索的抗弯刚度为302 N/m，用EI表示；边界处的弹性约束刚度用k1和k2表示，取值均为104.1 N/m；实测振动频率与索的索力关系如图2 所示。

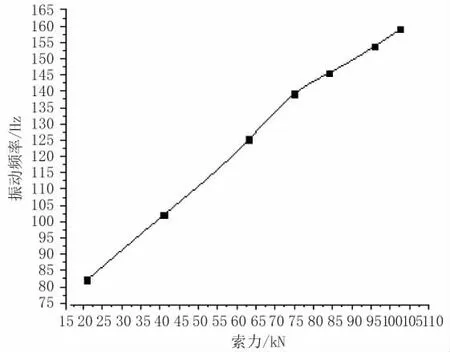
图2 索力与振动频率变化关系

根据实测数据和相关频率换算公式求得参数θ，从上述索力和振动频率数据相关性可以看出，模态参数识别法识别出的索力是精确的。

2.3.2 以拱桥索力为例

以某市1 座下承式拉索拱桥为例，拱桥位于边跨位置，是下承式提篮拱系杆拱桥，跨径100 m，桥梁全断面宽57 m，拱肋使用钢箱梁结构。拱桥吊杆由相互平行的高强镀锌钢丝组成，用HDPE 做拉索保护套。本桥梁索力边界条件较明确，受力模型简化为一端铰支、一端固支。

相关计算参数线密度m 由厂家提供数值，按照边界条件来确定计算吊杆索力长度l。

在本工程中取该桥5 根长度和位置不同的吊杆进行相关测试计算，计算的参数值和现场实测振动频率参见表1。

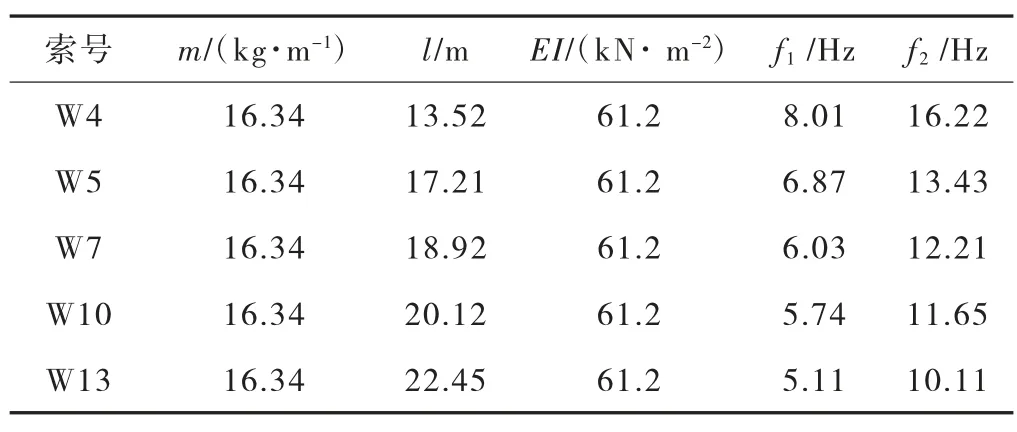
表1 吊杆参数及其固有频率

现场实测时，小于5 m 长度的过短吊杆索力测量值与索力标定值相差很大，所采集的是受到干扰较大的振动频率，导致其准确性无法得到保证。

现场为尽可能使索力标定值与索力实测值接近，采用千斤顶油压表和压力传感器同时进行标定，根据千斤顶和传感器的实测值选取索的固有频率。经过分析比较，千斤顶油压表测出的索力值精度较高，故最终采用该值作为索力标定值。

表2 是基于边界条件对索力测量的影响，采用各公式计算的索力。

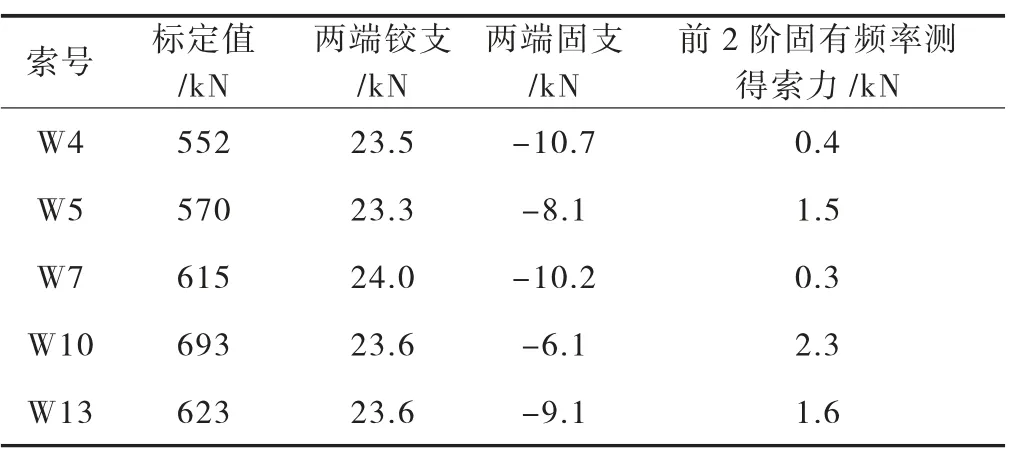
表2 边界条件影响下的索力计算结果

在实际工程中理想状态很难实现，主要原因是吊杆惯性矩难以准确确定。吊杆截面不受力时由独立钢丝组成，没有粘结，理论吊杆惯性矩为各钢丝惯性矩之和，计算的抗弯刚度为最小值。在实际工程中吊杆惯性矩在受力中不可忽略，此时应考虑钢丝束的整体作用。实际工程中的抗弯刚度值应介于最小值与最大值之间，但由上述分析可知，由于吊杆内部结构形式、索力大小等不确定因素的影响，其值很难得到准确识别。

3 结 语

（1）索力模态参数识别法是由振动频率法同时识别出拉索索力和抗弯刚度的。使用该方法计算简单，识别容易，精确度较高。

（2）拱桥吊杆索长度较短时（小于5 m），振动频率受外界干扰较大，因此对于短吊杆索的测量不适用于振动频率法。

（3）吊杆索的钢丝粘结度、吊杆索边界约束条件、索力大小、索结构形式及长度都会影响对索力的精准识别。

（4）推导的基于能量平衡原理的索力计算公式可以在不同边界条件下准确识别和提取吊杆索固有频率，考虑索力影响因素较为全面（边界条件和抗弯刚度的影响）。该方法避免了实际工程中抗弯刚度识别难的问题，计算过程简捷，计算结果精度较高，实用优势明显。