斜交条件下预制拼装地道结构设计研究
钱文斐,李忻轶,姜 炯
[上海市政工程设计研究总院(集团)有限公司,上海市 200092]
0 引 言
目前,对于桥梁[1]、综合管廊[2]、沉管隧道[3]、矩形盾构隧道[4]等正交条件下的矩形箱型结构已开展了大量的预制拼装工艺研究并付诸于工程实践中。本文以上海S7 公路一期工程为例,针对斜交条件下预制拼装地道结构进行分析研究,以期为矩形箱型结构预制拼装工艺的进一步拓展提供借鉴。
1 工程概况
上海S7 公路一期工程为上海市预制拼装示范工程,预制拼装化率超过95%。其中联杨路下穿G1501,共有 2 处地道,分别为 NE 匝道、SE 匝道。
工程所处地形较为平坦,场区浅层存在软土、厚填土、明浜等不良地基地质现象,对设计施工存在一定影响。自上而下主要岩土层分布情况如下:①1层填土、②层黄- 灰黄色黏土、③层灰色淤泥质黏土、④层灰色淤泥质黏土、⑤1层灰色黏土、⑥层暗绿-黄色粉质黏土。场地内地下水类型有潜水及承压水,地下水位随气候、季节及环境影响而变化。勘察期间,地下水位埋深为0.58~3.10 m,高程为4.25~0.06 m,承压水对本工程无影响。
本文拟以NE 匝道为例,对斜交条件下预制拼装地道结构受力情况进行分析研究。NE 匝道地道斜交角度为67°,垂直于轴线方向的结构宽度为16.0 m,其中结构净空宽度为14.6 m,侧墙厚度为0.7 m;结构高度为6.25 m,其中结构净空高度为4.85 m,顶、底板厚度均为0.7 m。
NE 匝道地道平面面、横断面、剖面见图1~图3。
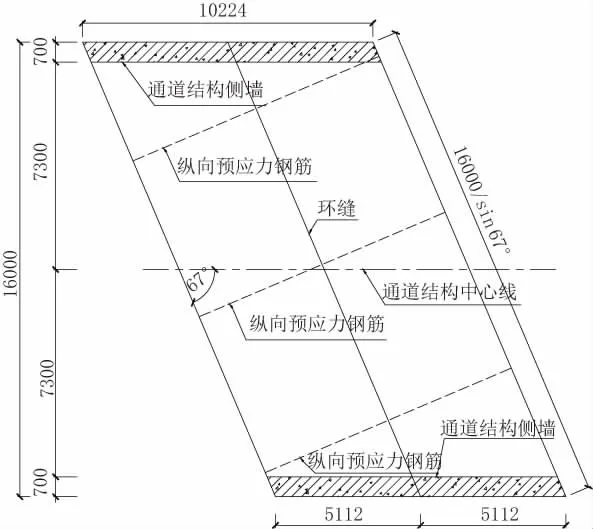
图1 NE 匝道地道平面图(单位:mm)
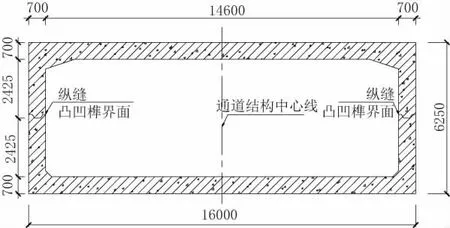
图2 NE 匝道地道横断面(单位:mm)
为了便于预制节段制作、运输,吊装,地道结构轴向与斜边平行分为2 块,横断面分为上下2 块“C”型结构,共形成4 个单元,单个单元的尺寸为17.382 m×5.112 m×3.125 m,质量约 213.3 t。
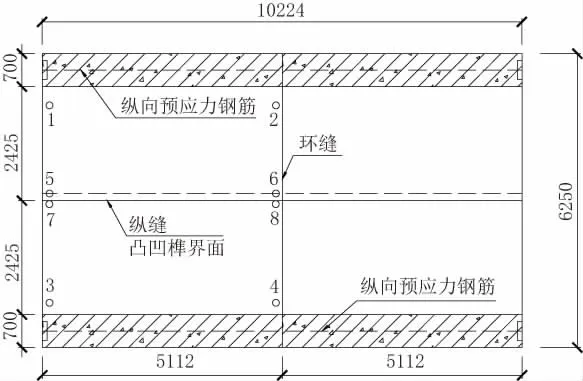
图3 NE 匝道地道剖面(单位:mm)
对于纵向接缝,采用垂直于斜边的预应力钢筋形式;对于环向接缝,采用凸凹榫形式,与通常环向接头形式的不同之处在于其未设置竖向预应力钢筋;纵、环向接缝间均匀涂抹环氧拼缝胶。
纵向预应力钢筋接头大样图见图4,环向凸凹榫接头大样图见图5。

图4 纵向预应力钢筋接头大样图(单位:mm)

图5 环向凸凹榫接头大样图(单位:mm)
2 结构计算模型
对于预制拼装结构,需进行吊装、运输及运营3种工况下的受力分析。考虑到吊装、运输工况下受力分析相对简单,本次重点研究运营工况。采用三维实体单元模拟结构,针对环缝设置凸凹榫接头的预制拼装结构体系(以下简称“体系一”)与封闭框架的现浇结构体系(以下简称“体系二”)2 种结构体系受力性能进行对比分析。
结构计算软件采用Midas/Civil, 主体结构采用六面体实体单元(见图6),凸凹榫界面采用仅受压弹簧模拟,底板边界条件采用弹簧模拟,基床系数为20 000 kN/m3。

图6 三维实体单元计算分析模型
荷载基本组合条件下,荷载值分布情况见图7。

图7 荷载基本组合示意图
3 结构受力及变形
基于结构安全考虑,地道结构的顶、底板及侧墙均按受弯构件进行计算,计算出弯矩值即可进行配筋设计。根据软件后处理成果输出方式及参照现行《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)条文说明4.2.4,需将三维实体单元输出的正跨方向应力值转换为顶、底板斜跨方向弯矩值及侧墙正跨方向弯矩值。具体思路如下:
首先,根据式(1)算出侧墙正跨方向的弯矩值;然后,根据式(2)计算顶、底板斜跨跨中方向弯矩值;最后,根据式(3)计算顶、底板斜跨支座处弯矩值。

式中:M 为正跨方向弯矩值;W 为截面抗弯模量;σ+(-)为截面正跨方向最大正(负)应力值。

式中:M铰正为顶、底板构件在铰接支撑边界条件下计算跨度为15.3 m(正跨方向)的跨中弯矩值;M铰斜为顶、底板构件在铰接支撑边界条件下计算跨度为15.3/sin 67° m(斜跨方向)的跨中弯矩值。

式中:M固正为顶、底板构件在固定支撑边界条件下计算跨度为15.3 m(正跨方向)的支座处弯矩值;M固斜为顶、底板构件在固定支撑边界条件下计算跨度为15.3/sin 67° m(斜跨方向)的支座处弯矩值。
3.1 顶板
体系一的顶板顶、底面正跨方向应力分布见图8、图9。
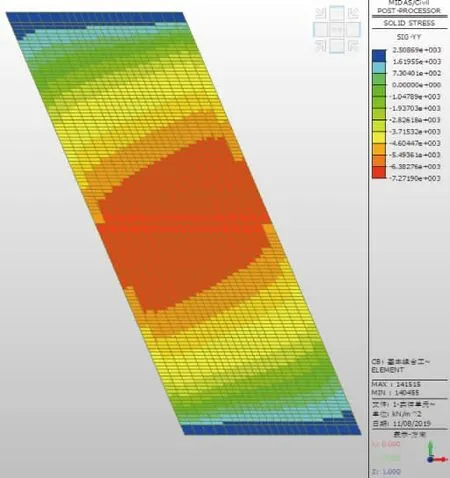
图8 顶板顶正跨方向应力云纹图
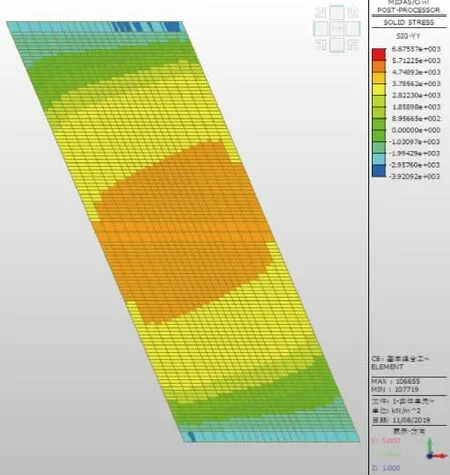
图9 顶板底正跨方向应力云纹图
体系二的顶板顶、底面正跨方向应力分布见图10、图11。

图10 顶板顶正跨方向应力云纹图
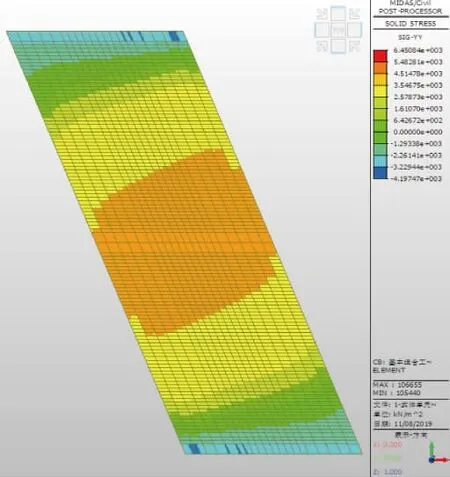
图11 顶板底正跨方向应力云纹图
顶板顶、底关键位置的应力差值见表1。

表1 顶板顶、底正跨方向应力差值一览表
由图8~图11 和表1 可知:2 种体系下,顶板顶、底正跨方向应力分布形态相近,且应力差值相差不大,即弯矩值相差不大,2 种体系下的差值范围为3%~10%。
3.2 底板
体系一的底板顶、底面正跨方向的应力分布见图12、图13。
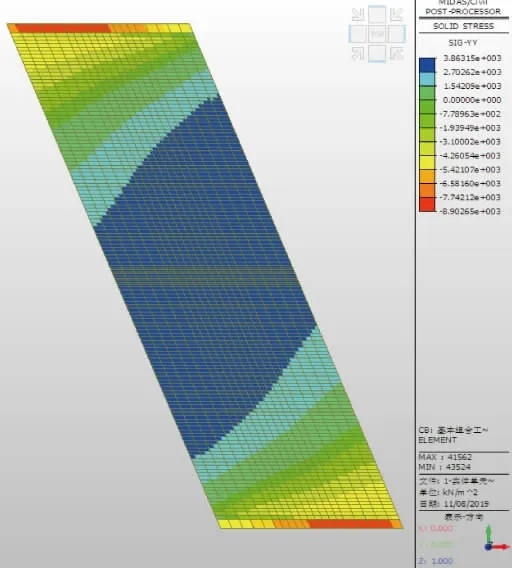
图12 底板顶正跨方向应力云纹图
体系二的底板顶、底面正跨方向应力分布见图14、图15。
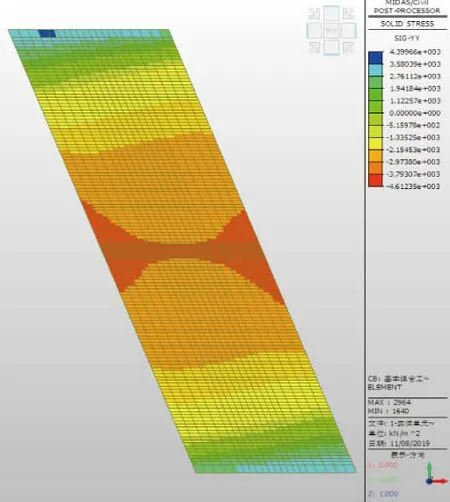
图13 底板底正跨方向应力云纹图

图14 底板顶正跨方向应力云纹图
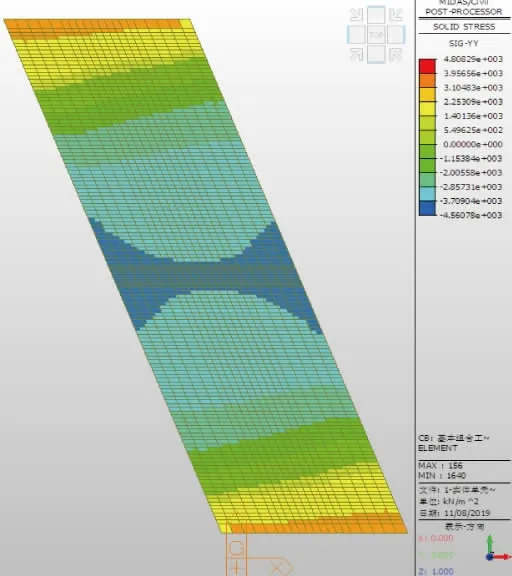
图15 底板底正跨方向应力云纹图
2 种体系下,底板顶、底关键位置应力差值见表2。
由图12~ 图15 和表2 可知:2 种体系下,底板顶、底正跨方向应力分布形态相近,且应力差值相差不大,即弯矩值相差不大,2 种体系下的差值范围为5%~13%。
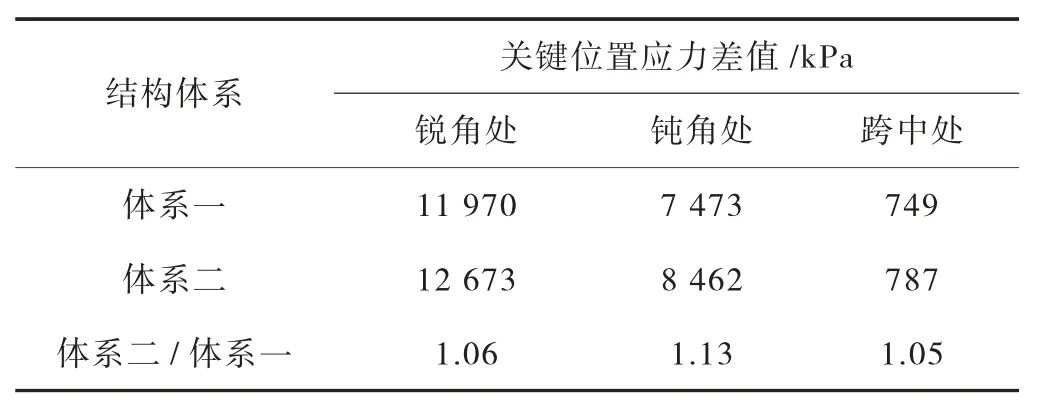
表2 底板顶、底正跨方向应力差值一览表
3.3 侧墙
体系一的侧墙临、背土侧正跨方向应力分布见图16、图17。
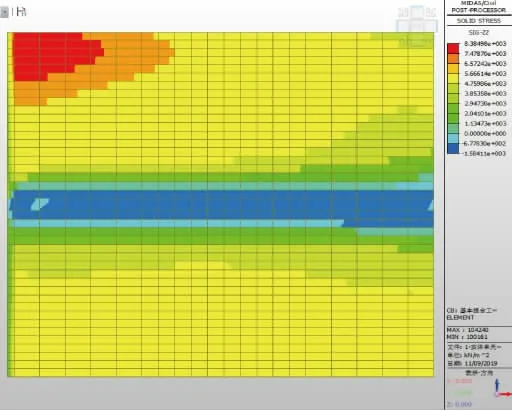
图16 侧墙临土侧正跨方向应力云纹图
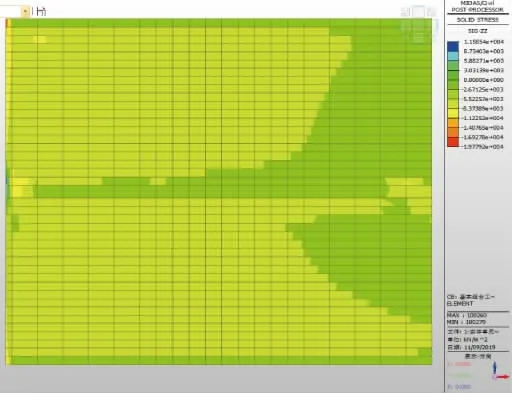
图17 侧墙背土侧正跨方向应力云纹图
体系二的侧墙临、背土侧正跨方向应力分布见图18、图19。
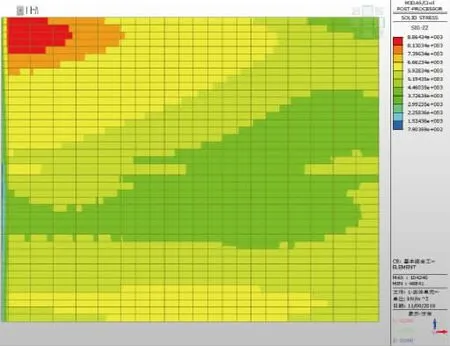
图18 侧墙临土侧正跨方向应力云纹图

图19 侧墙背土侧正跨方向应力云纹图
2 种体系下,侧墙迎土侧、背土侧关键位置应力差值见表3,点1~点8 的具体位置见图3。
由图16~图19 和表3 可知:2 种体系下,侧墙临土侧、背土侧正跨方向应力分布有一定的差别,侧墙与顶、底板交接处点1~ 点4 的应力差值(即弯矩值)相差范围为3%~11%,在凸凹榫位置附近点5~ 点8的应力差值(即弯矩值)相差范围为7%~22%。
3.4 凸凹榫处应力
体系一凸凹榫处最大主应力绝对值(见图20)在临土侧基本为拉应力,其分布范围约占1/4, 最大值为-6 331.6 kPa;而在背土侧基本为压应力,其分布范围约占3/4,最大值为12 481.1 kPa。
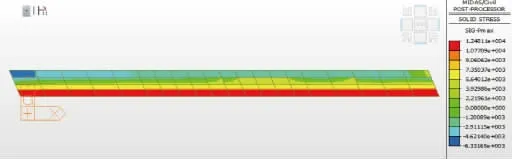
图20 凸凹榫处最大主应力绝对值云纹图
体系二相同位置处最大主应力绝对值(见图21)在临土侧基本为拉应力,其分布范围约占1/2, 最大值为-5 885.8 kPa;而在背土侧基本为压应力,其分布范围约占1/2,最大值为3 215.1 kPa。
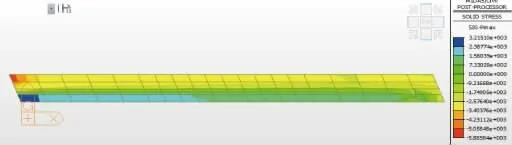
图21 相同位置封闭框架体系最大主应力绝对值云纹图

表3 侧墙迎、背土侧正跨方向应力差值一览表
综上可知:(1)2 种体系相同位置临土侧结构单元最大主应力均呈现拉应力,而背土侧结构单元均呈现压应力,从而产生弯矩作用;(2)凸凹榫与封闭框架体系相同位置临土侧拉应力比值为1.08,背土侧压应力比值为3.88。
3.5 凸凹榫接缝处张开值
进一步研究体系一凸凹榫接缝处的张开值。
凸凹榫接缝处节点位移见图22 和表4。

图22 凸凹榫处位移
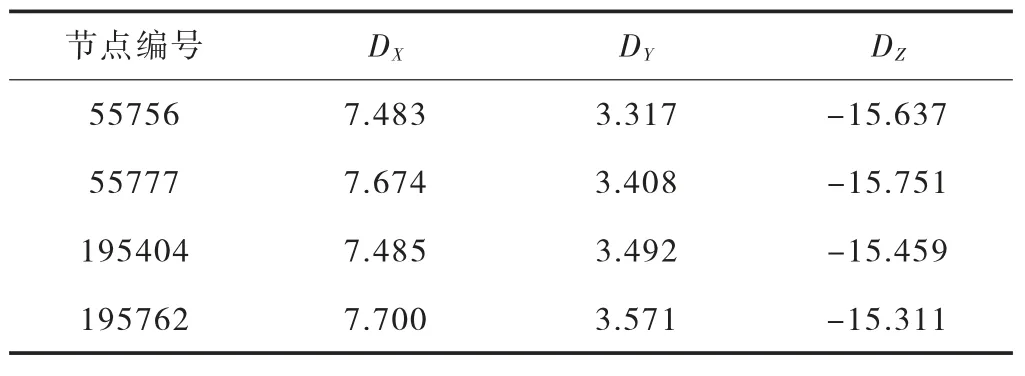
表4 凸凹榫处节点位移一览表 mm
通过以上计算分析得出:结构侧墙凸凹榫处发生了向临土侧的位移,接缝处最大张开值为0.44 mm(节点195762 与节点55777 在 Z 方向上的位移 DZ之差值,即 -15.311 -(-15.751)=0.44),接缝处张开值与现场观测结果基本一致。
4 结 语
(1)对于斜交条件下预制拼装地道纵缝采用凸凹榫接头的结构体系,顶板、底板、边墙(除凸凹榫位置外)关键位置处的弯矩值与封闭框架体系下的差别不大,差值基本在13%以内。
(2)工程设计通常假定凸凹榫处采用铰接边界条件模拟,这样计算的结果为凸凹榫处不承受弯矩,且水平向位移值较大。而本次研究成果为凸凹榫处由于拉、压应力可以产生弯矩,且水平位移值仅为铰接条件下的40%(按铰接计算,水平位移值为18.2 mm)。这说明对于凸凹榫接缝采用铰接进行模拟存在不合理之处。
(3)为了方便工程设计中的结构计算分析,体系一的受力计算模型可考虑利用体系二的等效计算模型,但需将凸凹榫位置处弯曲值进行适当提高,为安全起见,可考虑提高20%~30%。
(4)本研究成果已运用于上海S7 公路一期工程中,并取得了良好的经济效益及社会效益。整个工程已于2019 年10 月18 日全线通车。本研究成果可以为类似工程提供参考与借鉴。

