在强化教材分析的基础上优化教学设计——以“等差数列的前n项和”为例

石志群

发展学生数学核心素养是2017 年版高中数学课程标准提出的要求，而数学基础知识因其经典性、基础性成为实现这一目标的重要载体。笔者认为，对教材中的基本内容进行强化分析、深化认识、把握本质是提高教学设计水平，发展学生数学素养的根本途径。本文以“等差数列前n 项和”为例对此作初步探索。

一、内容基本点分析

笔者先对本节内容的三个基本点作梳理。

1.问题情境。

等差数列的问题情境通常有两类：现实情境和文化情境。

问题的现实情境较多，常见的有：

①花坛有若干层，各层花盆数依次成等差数列，求花坛上花盆总数（类似的，货架上货物总数的计算，求一堆钢管总数等）；

②单利存款，本利总和；

③从材料工地运送电线杆到500 米以外的公路的同一旁埋设，每隔50 米在路边埋一根。已知每次只能运3 根，要完成运24 根电线杆的任务，并返回材料工地，问运输车的行程是多少米？

文化情境有：

①毕达哥拉斯学派的“三角形数”；

②高斯的故事；

③中国古代的“垛积术”（高阶等差数列求和）中最基础的数列——等差数列。

创设的问题情境既要能提出本节课要研究的问题，又要能与推导方法产生思维的链接，还要尽量避免过分的“启发”，否则使学生由情境本身直接知晓推导方法，会掩盖思维的过程。当然，情境不宜复杂，以免冲淡主题，加大学习难度，要以简单而蕴含本质的情境引入，促使学生比较容易地提出本节课的研究问题（主题）。换言之，情境的创设要力求入口浅、寓意深。

2.等差数列的表征方式。

数学对象的表征方式对数学思维活动起着一定的启发、诱导作用，善于运用不同方式对数学对象进行表征，并由表征方式产生联想是一种重要的数学素养。

等差数列是一种基础的、重要的数列模型，从数学史看，其表征方式主要有——

（1）定义表征：an-an-1=d（n∈N*，n≥2）。

（2）代数表征：通项公式an=a1+（n-1）d，或函数形式an=an+b。

（图1）

（3）几何表征有3 种：形数表征，如三角形数、四边形数等（见图1）；图象表征，即一次函数中自变量取正整数的点列（见图2）；面积表征，即分别以公差d 为底边（在x 轴上），以an为另一条边（有向线段）构成的系列矩形（见图3）。

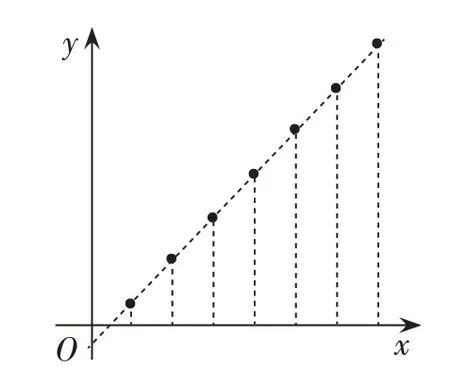
（图2）

（图3）

3.探索路径。

基于等差数列的代数和几何表征，可得到两种探索等差数列前n项和的思路。

以上思路还是比较自然的，难点是如何自然地链接到本节课的核心内容——“倒排相加法”。关于这一点，可从几何表征的思路中获得启发。

（2）几何表征下的思路。对于图1，就是求图中点的总数。在此处可以引导学生联想几何中是如何求三角形的面积的。于是“补形”的思路就自然出现了（即用一个全等的三角形“倒扣”上去，补成一个平行四边形，图略）。

与此类似地处理图2、图3，将不“规则”的图形补成规则的图形，将未解决的图形补成已经解决了的图形。这里的“补形”体现的就是“倒排相加”的思想，将变化着的项的求和转化为常数列的求和。因此，只要将图形意义用代数符号表示出来，就能自然地得到倒排相加法。

如何解决代数表征下引导学生自然地想到倒排相加的方法呢？

此外，还可以从数学审美的角度反思求1+2+3+…+100的过程，配对法的思维过程是：

首项与末项的和：1+100=101

第2项与倒数第2项的和：2+99=101

第3项与倒数第3项的和：3+98=101

……

第50项与倒数第50项的和：50+51=101

如果用于求1+2+3+…+100+101的值，就会“多”出一项“51”没有与之相配的项，而相同的问题却用不同方法，显得不够“美”，怎样才能美呢？完整是美、一致是美、对称是美，于是，我们就要反思：在和式中的项的地位是一样的，为什么配对时到了“50”就停了？这个“工作”应该继续下去：

1 + 100 = 101

2 + 99 = 101

3 + 98 = 101

……

50 + 51 = 101

51 + 50 = 101

……

100 + 1 = 101

这样，两个公差互为相反数的等差数列跃然纸上，而且无论n 取奇数还是偶数，方法就统一了。这个方法不仅适用于特殊的等差数列，而且适用于一般的等差数列。

二、教学思考

1.数列研究的核心问题是什么？

从各种教科书上可以看到，数列（包括各种特殊的数列），其研究的内容主要是通项公式、性质及若干项的和。这说明，“和”是数列这一数学分支的主要研究问题之一；同时也说明，“通项”与“和”是其核心问题（性质即为“项”与“和”及其之间具体的特性及关系）。关于“和”，一方面其在现实中有广泛的应用（商场中的货架上堆放的商品总数、银行存款中的若干模型等），另一方面函数的级数表示正是数列和的形式，它体现了人们认识变化世界的观念和方法的巨大进步，也是数学应用于现实的重要途径。

总之，“和”应该是数列研究的核心问题之一。

2.为什么求等差数列前n 项和可用倒排相加的方法？怎么想到倒排相加的方法的？

在教学中不能用高斯的思考结果替代学生的探究性思维；不能用钢管堆的原型作为初始问题，立即给出倒排相加的思路，否则就掩盖了问题的抽象过程，对思路作出了过度的告知。

事实上，我们非常重视几何中的“割补”方法，经常运用这种方法将不规则的形、体转化为规则的形、体，将不熟悉的形、体转化为熟悉的形、体，但我们忽视了其与代数中的类似的数学技巧的沟通与联系。在代数中我们也常通过配凑、添减等技术处理代数式，进行问题的转化，这与几何中的“割补”法在思想上是一致的。有了这种认识，解决上面的“为什么”“怎么想到的”等问题就比较容易了，因为这种思想方法在几何中已经有了应用，几何的直观也更易于为学生所理解。

3.等差数列的基本特征是什么？

从数的角度看，等差数列的“逆序”排列所得数列仍是一个等差数列，即若等差数列a1，a2，…，an的公差为d，则有数列an，an-1，…，a2，a1是公差为-d的等差数列，即有Sn= a1+a2+a3+…+an=a1+（a1+d）+（a1+2d）+…+［a1+（n-1）d］且Sn=an+an-1+an-2+…+a1=an+（an-d）+（an-2d）+…+［an-（n-1）d］。由此也容易发现两个式子相加的思路。

4.“倒排”相“拼”的本质是什么？

我们知道，平行四边形的面积公式是基于“祖暅原理”的，即“用平行于底边的直线截，所截得的线段均相等”。而图1 这样的等差数列几何表征，拼出来的四边形也具有类似的特性：每一行中点的个数都是相同的。因而，通过“拼凑”，使得“变”变为“定”（将一般的等差数列转化为特殊的等差数列——常数列），便是“倒排”相“拼”的本质。

三、教学设计建议

基于上述分析可以发现，等差数列求和公式既有着广泛的应用价值，也有着深刻的数学背景，还蕴含丰富的文化内涵，合理地进行教学设计，可以增强学生的数学应用意识，发展理性思维，培养关键能力，提升数学素养。

笔者建议，可以用含实际背景的问题情境进行引入，提出本节课的核心问题：等差数列前n 项和如何求？可以是具体的等差数列，也可以是一般的等差数列。如果是后者，学生容易由通项公式转化为前n个自然数的和。

如果学生想到高斯用配对法求和的思路，可以先重复一下求和过程，再研究一般的问题。这样学生自然会想到分成偶数个项与奇数个项进行讨论。

接着再从数学审美的视角反思配对法，提出问题：为何同一问题却用不同的方法解决？追求统一是数学的基本价值要求，应该找到不分项数是偶数还是奇数的一致方法；引导学生对和式中的各项地位均等进行认识，想到将“配对”的工作继续进行下去的思路，从而发现倒排相加的思路。

在从代数表征的视角解决问题后，再提出问题：数学对象通常可从“数”与“形”两个形式进行表征，因此，如何“几何地”表示出等差数列中的项呢？如何将“数之和”转化为“几何对象的某种度量之和”？从而想到从几何角度的解决方法：补形法。

具体的教学设计这里就不完整写出了。需要说明的是，在上面的过程中，可以将相关的文化元素揭示出来，给学生提供延伸阅读的材料，如与“垛积术”相关的数学史料。