冲击载荷作用下典型发射药的弹性模量分析方法

刘计划， 赵宏立， 何昌辉， 靳建伟， 张邹邹， 王琼林， 赵宝明

(西安近代化学研究所， 陕西 西安 710065)

0 引言

为了提高火炮的初速，普遍采用提高发射药能量及增大发射装药装填密度等方法。在发射药中加入高能固体颗粒可显著提高发射药的能量，而高能固体颗粒的加入，会显著改变发射药力学性能，尤其是低温下的力学响应，增加了突发胀膛和炸膛的风险，严重影响火炮发射安全性[1-2]。引起此风险的原因，主要是发射药粒在发射过程中产生的冲击挤压破碎造成的[3-5]。近年来，一些学者已对此问题开展了多年研究，其中利用数值仿真的手段模拟发射药冲击破碎过程是很重要的一个方面[6-7]。而发射药的弹性模量作为仿真过程中的一个力学参量，是必不可少的，其关乎仿真结果的真实性，进而影响分析过程及结论的准确性。因此，如何准确合理的获得发射药弹性模量，是个值得深入研究的问题。

目前弹性模量的计算方法采用的多是提取发射药在压缩/冲击实验中应力与应变曲线初始线性段的斜率来得到[8-10]，但发射药作为一种黏弹性(VE)材料，采用上述方法的合理性有待讨论。此外，由于发射药的特殊性，无法直接测量受载过程中发射药表面的形变，只能间接得到其轴向应变。为解决这一问题，一种全场无接触的光学测量方法——数字图像相关方法被用于测量发射药在冲击过程中的位移/应变，此方法具有0.01像素以上的理论精度[11-14]；结合高速摄像机(在线跟踪冲击过程中发射药表面的灰度图像)，可实现发射药变形的实时监测，并确保数据的真实性和准确性。目前，作为安全性的重要组成部分，发射药力学性能的评价主要是以基本的力学实验为主，获得的往往是表观的力学性能。而发射药内部的损伤演化特征关乎到发射药粒构型及配方设计的合理性，通常使用仿真分析的手段开展此类研究。而通过本文的研究，可为发射药的力学性能评价提供数据及技术支撑，为发射药配方及构型设计提供理论指导。

本文主要利用线弹性(LE)、非线性弹性(n-LE)和VE[15-16]3种不同的分析手段，结合高速摄像技术及数字图像相关方法，对发射药在低温和常温冲击载荷作用下的弹性模量进行研究，以求对在不同假设条件下发射药的弹性模量有较为深入的认识。通过3种方法的对比，来确定发射药弹性模量最优的分析方法，并说明数字图像相关方法用于分析发射药冲击变形的有效性。

1 实验过程与数据处理

1.1 实验过程

本文所用DAGR125-21/19发射药以硝化棉(NC)为基体，以硝化甘油(NG)为增塑剂，并含有一定量的叠氮硝胺及黑索今等组分；所用双芳-3发射药是以NC为基体，以NG为增塑剂的双基发射药，均由西安近代化学研究所提供；落锤冲击实验机型号为CEAST 9340(自带温控箱)，由美国Instron公司提供；高速摄像机型号为VEO 710，由美国Phantom公司提供；数字图像相关方法的计算软件为GOM Correlate 2018，由德国GOM公司提供。

实验前，对发射药试样进行处理，确保其尺寸基本保持一致。之后，对发射药样品表面进行散斑制作(如表1所示)，获得散斑分布均匀的试样。已喷涂散斑的试样静置4 h以上，将喷涂散斑试样放置于保温箱中，设置到规定温度，保温4 h进行落锤冲击实验。低温和常温的落锤冲击实验的参数设置，如表2所示。

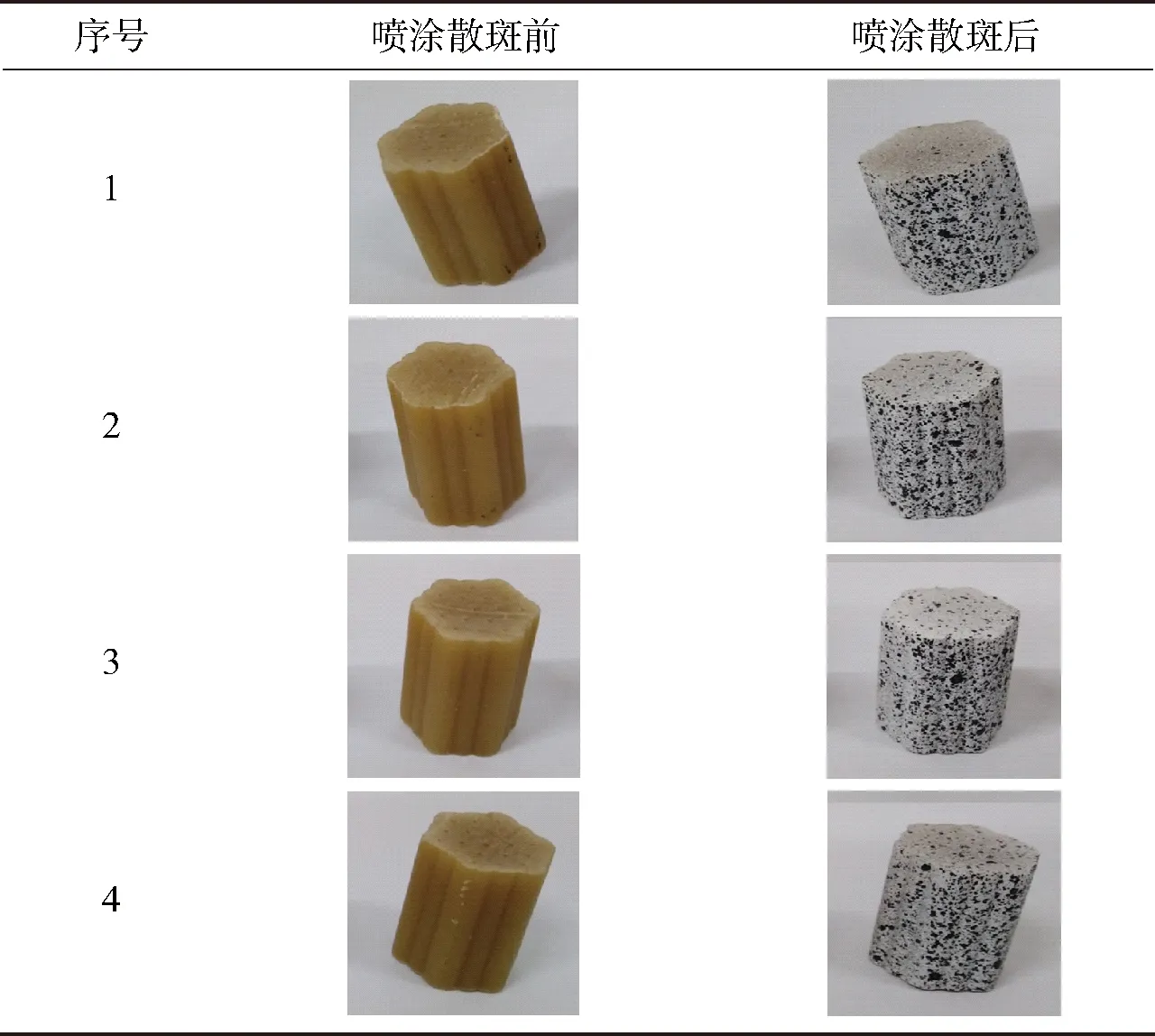
表1 DAGR125-21/19发射药试样喷涂散斑后的状态

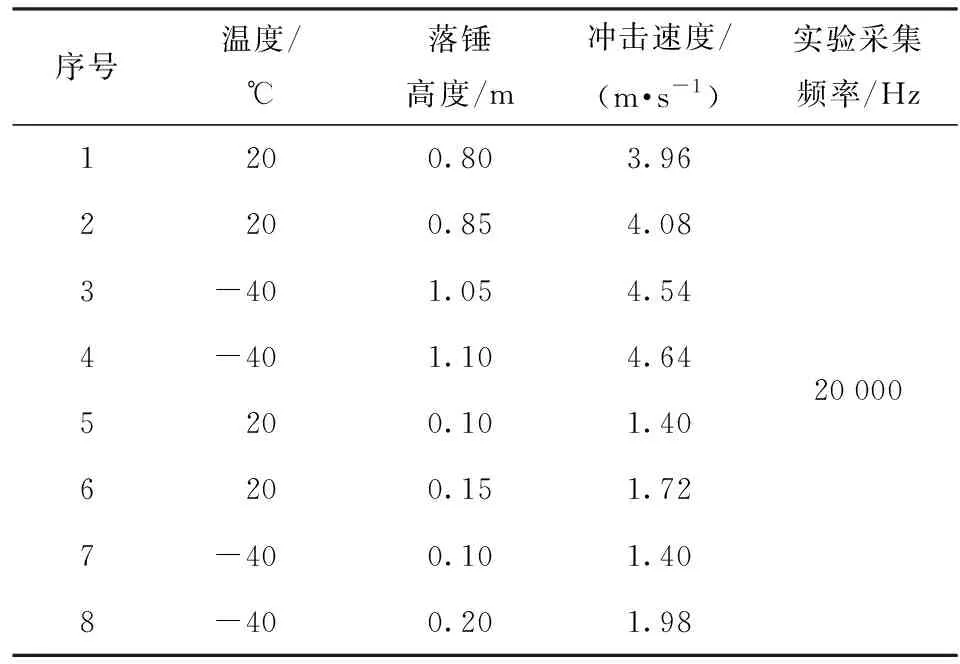
表2 落锤冲击实验中各组的参数设置

实验中，利用高速摄像机记录冲击过程，其中参数设置为：采集帧频为20 000 帧/s，位深为8 bit，分辨率为640×480像素。利用数字图像相关方法软件计算冲击过程轴向的应变随时间的变化规律，参数设置为：子区大小为19像素，步长为11像素。如图1所示是数字图像相关方法计算得到的DAGR125-21/19发射药落锤冲击实验中轴向的表面位移。

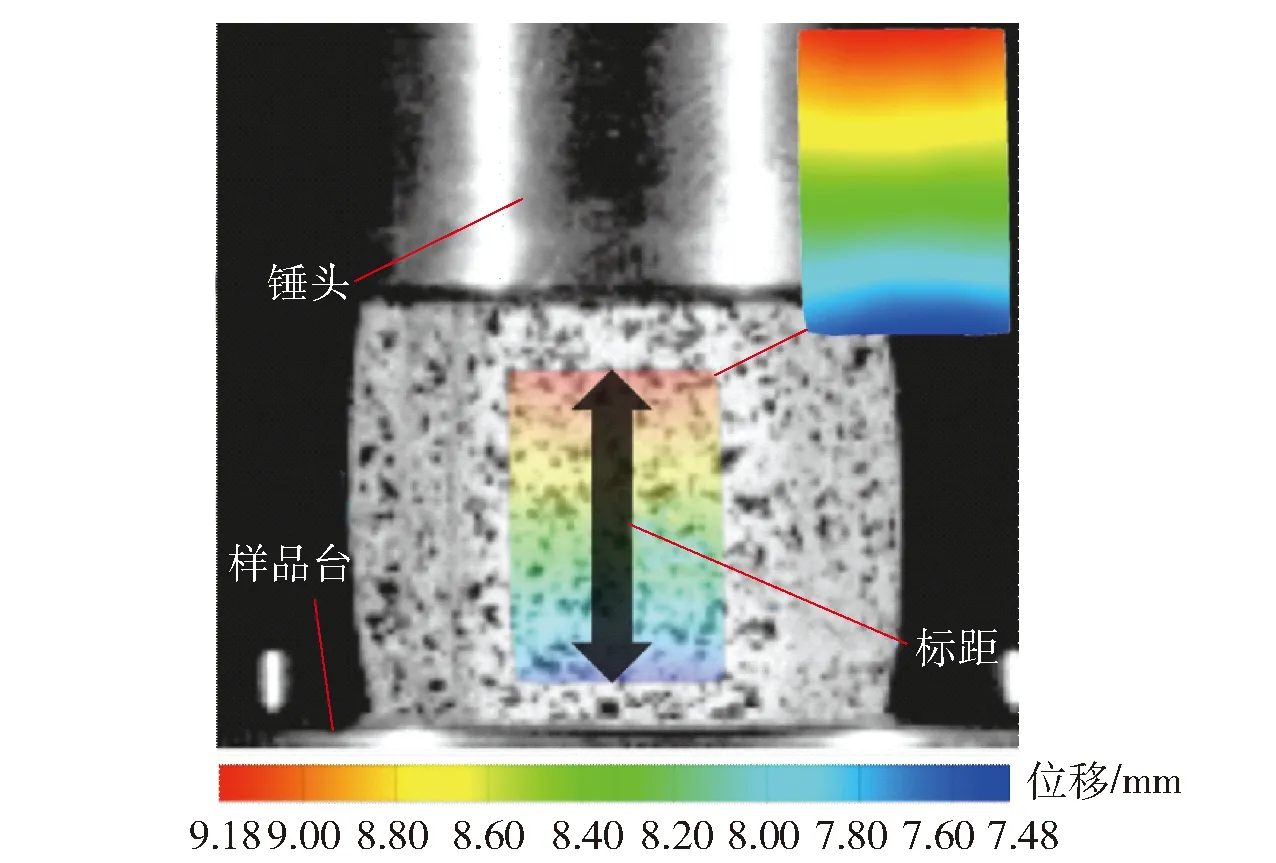
图1 由数字图像相关方法计算得到的DAGR125-21/19发射药轴向的表面位移Fig.1 Axial surface displacement of DAGR125-21/19 gun-propellant by digital image correlation method

1.2 数据处理

在这一部分的研究中，对于发射药弹性模量的分析，主要有3种方法：

1) LE分析。这种处理方式相对比较简单，主要是提取冲击过程中获得的发射药应力与应变曲线LE段线性部分的数据，利用(1)式，通过线性回归，得到其弹性模量：

σl=Elεl+σ0，

(1)

式中：σl为冲击实验中应力与应变曲线线性段的应力；El为LE分析中获得的发射药在冲击载荷作用下的弹性模量；εl为与σl对应的线性段应变；σ0为应力与应变曲线弹性段线性部分延长线与横轴的交点所对应的应力。

2) n-LE分析。已有的研究表明，聚合物在冲击载荷作用下的动态本构关系中非线性仅来自于纯弹性响应，故在这一部分分析中，主要利用应力与应变曲线整个弹性段的数据为研究对象进行相关分析。此时，已知应力与应变为非线性的函数关系，对其进行幂级数展开，取前3项，可得(2)式，利用此公式对弹性段非线性部分进行拟合，可得此时的弹性模量：

(2)

式中：σe为冲击实验中应力与应变曲线弹性段的应力；Ee为非线性分析中获得的发射药初始弹性模量；εe为对应于σe的弹性段的应变；α、β为计算得到的n-LE系数。

3) VE分析。以在高聚物本构关系中应用较多的“朱- 王- 唐”模型为基础，考虑应变率效应或时间依赖性，分析发射药的本构特性。此模型对于典型高聚物(包括热塑性和热固性)的非线性VE本构关系具有很好的表征效果。发射药本质上是一种高分子材料，理论上可利用此模型对其进行分析。具体表达式如(3)式所示：

(3)

图2 VE分析的流变模型Fig.2 Rheological model of viscoelastic analysis

式中：σv为冲击实验中应力与应变曲线VE段对应的应力；Ev为VE分析中得到的初始弹性模量；εv为与σv对应的VE段的应变；α、β为VE分析中计算得到的n-LE系数；积分项描述的是应变率下VE响应，t为加载时间，τ为表征时间的变量，EM和θM分别为所对应的Maxwell单元的弹性常数和松弛时间。此模型的流变学模型如图2所示，其中ηM为粘度。从(3)式可以看出，应力是应变、应变率及时间3个参量的函数。为了分析方便，利用(4)式描述应变率与时间的关系。然后代入(3)式，使其转变为应力与应变和时间的关系，从而简化计算。

(4)

式中：A、B、C为待定常数。

2 结果与讨论

图3所示为基于数字图像相关方法得到的应变而建立的应力与应变关系，并根据VE和n-LE分析获得3组平行性实验(1号参数)的拟合结果。由图3可以发现：两种方法对实验数据的拟合效果表现良好；其中，在7%的应变范围内，前者具有很好的适用性。表3为利用3种分析方法得到的DAGR125-21/19发射药的弹性模量。从表3仔细观察发现：从数值上看，利用VE分析得到的发射药弹性模量最小，均值为473.68 MPa；而n-LE和LE的分析结果在数值上是相当的，均值分别为863.65 MPa和883.38 MPa，后者略大于前者。经过分析发现，通过n-LE和LE分析得到的弹性模量，大约是VE分析的2倍左右，按均值计算，分别为1.82倍和1.87倍。图4(a)所示为利用3种方法得到的两种冲击速度下DAGR125-21/19发射药的弹性模量；图4(b)为弹性模量的平均值及其标准偏差。由图4可以发现：随着冲击速度的增加，弹性模量变化很小；以均值为研究对象，随着冲击速度的增加，LE、n-LE及VE分析得到的弹性模量分别增加了6.16%、1.38%和1.26%，可见增加幅度很小。

图3 n-LE和VE两种分析方法对实验数据的拟合结果Fig.3 Fitting curves of experimental data by viscoelastic and nonlinear-elastic analysis methods

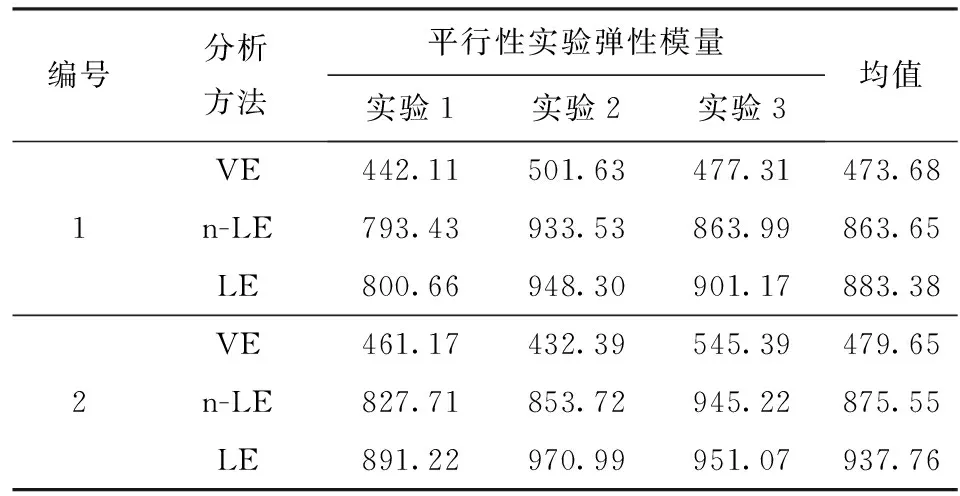
表3 3种不同分析方法得到的常温下DAGR125-21/19发射药弹性模量

图4 利用3种分析方法得到的常温下DAGR125-21/19发射药弹性模量及其均值和标准偏差Fig.4 Mean values and standard deviations of elastic moduli of DAGR125-21/19 gun-propellant by three analysis methods at room temperature

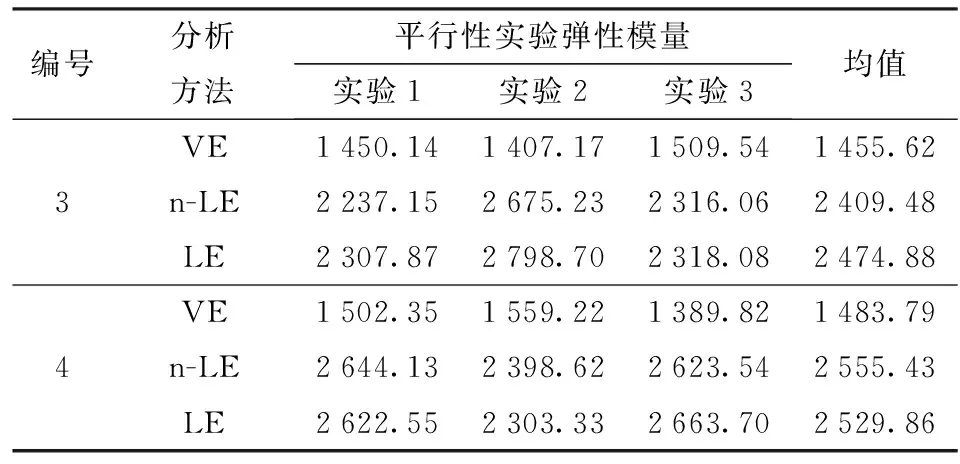
表4 3种不同分析方法得到的低温下DAGR125-21/19发射药弹性模量

这种现象的产生可归咎于弹性模量本身对加载速率的低敏感性，弹性变形在固体中传播是以介质中声速进行的，本文在落锤冲击实验中加载速率在4 m/s左右，远低于介质中声速，故在研究中，加载速率对弹性模量的影响甚微。

图5为DAGR125-21/19发射药在低温下的应力与应变数据(3号参数)，以及利用n-LE和VE分析得到的拟合结果。由图5可以发现，在11%应变范围内，两种分析方法对实验数据都有很好的拟合效果。表4是利用3种方法获得的两种冲击速度下DAGR125-21/19发射药在低温下的弹性模量，每组参数平行进行3组实验，取其平均值作为真值。与常温情况相似，3号实验参数下DAGR125-21/19发射药通过VE分析得到弹性模量相对于其他两种方法来说很小，均值为1 455.62 MPa. LE和n-LE两种方法得到弹性模量的均值分别为2 474.88 MPa和2 409.48 MPa，后二者分别是前者的1.70倍和1.66倍。图6(a)为两种冲击速度下DAGR125-21/19发射药弹性模量的对比结果；图6(b)为3种分析方法得到的低温下弹性模量的平均值及其标准偏差。由图6可以看出，当冲击速度增加后，弹性模量并没有明显增加，具体来说，随着冲击速度的增加，VE、n-LE和LE的分析结果分别增加了1.9%、6.1%和2.2%。此现象说明，冲击速度的改变对发射药弹性模量是有影响的，但由于弹性模量对加载速率的低敏感性，所以冲击速度的增加对DAGR125-21/19发射药弹性模量的改变影响很小。另外，从数值上看，低温下弹性模量远大于常温下弹性模量。以常温1号和低温3号实验结果作对比，低温下弹性模量的LE、n-LE和VE的分析结果是常温下的2.80倍、2.79倍和3.07倍。这一现象，一方面归咎于冲击速度的增加，但其主要原因是由于温度的降低造成的。低温会使发射药本身变成一种硬而脆的材料，刚度和硬度都会增加，从而使得DAGR125-21/19发射药在低温下的弹性模量远大于常温下弹性模量。

图5 低温下利用n-LE和VE分析方法得到的DAGR125-21/19发射药应力与应变拟合曲线Fig.5 Fitting curves of stress-strain by viscoelastic and nonlinear-elastic analysis methods at low temperature

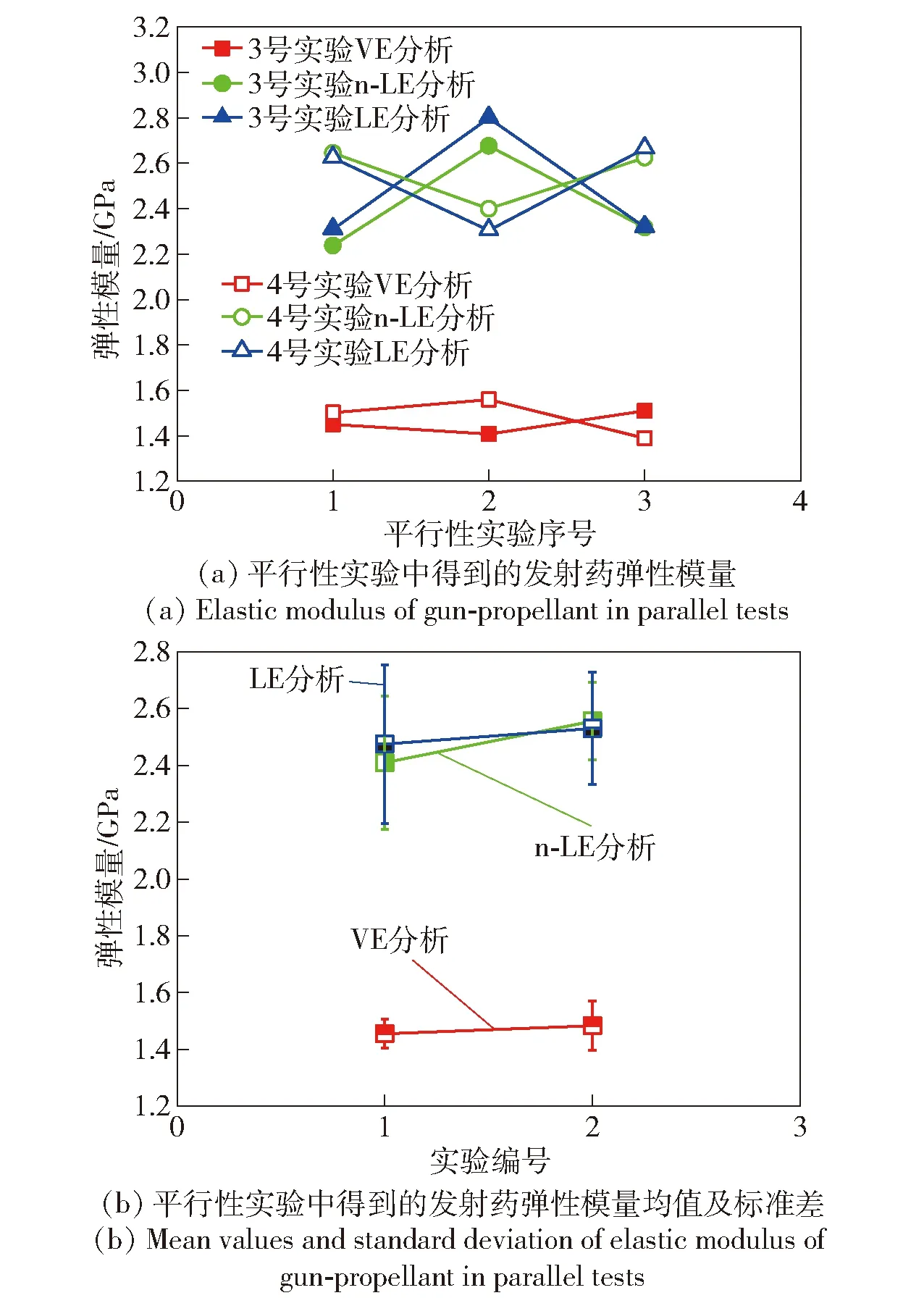
图6 利用3种分析方法得到的低温下DAGR125-21/19发射药弹性模量及其均值和标准偏差Fig.6 Mean values and standard deviations of elastic moduli of DAGR125-21/19 gun-propellant by three analysis methods at low temperature

对于双芳-3均质发射药，表5所示是其常温下5号和6号实验弹性模量的分析结果。由表5发现两种发射药弹性模量在数值上是相当的，且可以观察到与DAGR125-21/19发射药弹性模量有相似的现象：1)LE和n-LE两种分析方法的结果相近；2)VE方法得到的结果相对于其他两种方法要小很多；3)随着冲击速度的增加，弹性模量有小幅度上升。以上现象说明高能固体颗粒的加入对发射药常温下弹性模量影响很小。表6是双芳-3发射药低温下弹性模量的计算结果。由表6可以看出，低温下双芳-3发射药弹性模量相对于常温来说增长了5倍左右，而DAGR125-21/19发射药是3倍左右的涨幅。从数值上来看，双芳-3发射药低温下通过VE方法得到的弹性模量与DAGR125-21/19发射药利用LE和n-LE两种方法得到的结果是相当的，且在7号、8号实验中分别小于LE和n-LE分析结果的1.66倍和1.91倍、1.41倍和1.71倍。说明高能固体颗粒的加入对发射药低温弹性模量的影响很大。

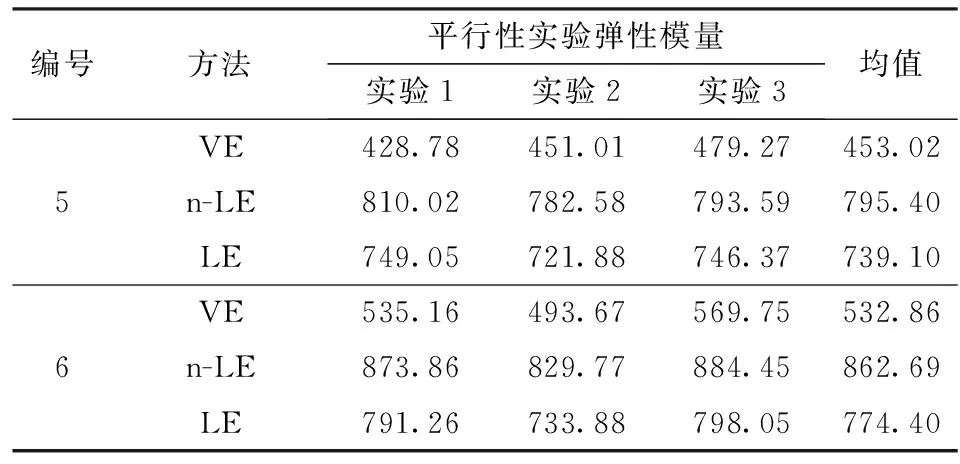
表5 3种分析方法得到的常温下双芳-3发射药弹性模量

综上所述，在常温和低温环境下，通过LE和n-LE分析得到的DAGR125-21/19发射药弹性模量在数值上相差不大，大约是VE分析的1.8倍(常温)和1.7倍(低温)左右。同时，由于弹性模量的应变率低敏感性，随着冲击速度的增加，DAGR125-21/19发射药弹性模量变化很小。而低温下，发射药变得硬而脆，刚度增加，使得弹性模量远大于常温下弹性模量，前者大约是后者的3倍左右。同时对双芳-3均质发射药常温下弹性模量进行了分析，可以得到与DAGR125-21/19发射药相似的结果，但由于高能固体颗粒的影响，低温条件下双芳-3发射药的弹性模量远大于DAGR125-21/19发射药。目前发射药领域大多采用LE分析，此方法主要借鉴金属材料分析力学问题的手段，以获得发射药的力学参数。但发射药是一种VE材料，与金属材料有很大差别。具体来说，作为线型聚合物的发射药，在受到外部载荷作用下会同时产生弹性形变和黏性流动。弹性形变是瞬时发生的，当发射药受到外力作用时，分子链内部键长和键角会立刻发生变化，从而产生弹性形变，是可恢复的。与此同时，分子间产生相对滑移，形成黏性流动，由此产生的形变是不可恢复的。可见，发射药在受到冲击载荷作用初期的变形是由弹性形变和黏性流动共同作用的结果。而LE法和n-LE法只考虑了前者，将初期的所有变形归功于弹性，这也是两种方法分析结果大于VE的原因之一。从这个角度讲，利用LE法和n-LE法分析发射药的弹性模量是不合理的，而VE法则是同时考虑了两种因素的影响。如若LE和VE分析获得的弹性模量相近，在保证计算精度前提下，为方便起见，可直接利用LE分析的弹性模量进行仿真分析。但从目前的结果来看，两种分析方法得到的结果相差很大，那么利用二者的弹性模量获得的仿真计算结果必然有所不同。故建议在发射药冲击破碎的仿真分析计算中，为了得到相对准确的结果，应使用VE分析得到的弹性模量。

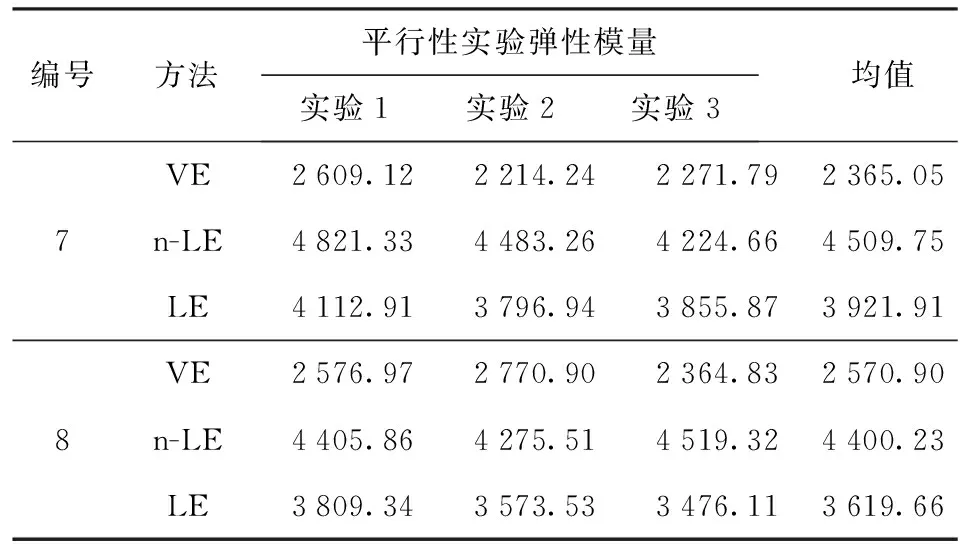
表6 3种分析方法得到的低温下双芳-3发射药弹性模量

以上分析皆是基于数字图像相关方法获得的轴向应变，考虑到方法本身的高精度，通过VE分析可获得冲击载荷作用下准确可靠的发射药弹性模量，从而证明了数字图像相关方法用于分析发射药冲击变形的有效性。

3 结论

本文基于数字图像相关方法获得的冲击载荷作用下发射药的轴向应变，利用LE、n-LE及VE等3种分析方法，针对常温和低温下DAGR125-21/19异质及双芳-3均质发射药的弹性模量开展研究，得到以下主要结论：

1) 通过LE和n-LE分析得到的发射药弹性模量在数值上相差较小，但大于VE分析的结果；在落锤冲击实验中，冲击速度的改变对发射药弹性模量影响很小。同时低温导致发射药刚度增加，使得获得的弹性模量远大于常温下弹性模量。

2) 高能固体颗粒的加入对发射药常温下弹性模量影响很小，但在低温下影响很大，导致双芳-3发射药低温下弹性模量远大于DAGR125-21/19发射药弹性模量。

3) 考虑到发射药的VE本质，以及LE、n-LE和VE3种分析方法结果的巨大差异性，故为了获得相对准确的分析结果，在发射药冲击破碎的仿真分析中，应使用VE分析获得的弹性模量。

4) 通过数字图像相关方法，结合VE分析，能够准确可靠地获得冲击实验中发射药的弹性模量，说明了数字图像相关方法用于分析发射药冲击形变的有效性。

参考文献(References)

[1] LIEB R J. Correlation of the failure modulus to fracture-generate surface area in uniaxially compressed M43 gun propellant [R]. Aberdeen Proving Ground, MD,US: Army Research Laboratory, 1995.

[2] 芮筱亭, 冯宾宾, 王国平. 发射装药发射安全性评估方法[J]. 兵工自动化, 2011, 30(5): 56-60.

RUI X T, FENG B B, WANG G P. Evaluation method of launch safety of propellant charge [J]. Ordnance Industry Automation, 2011, 30(5): 56-60.(in Chinese)

[3] 王永强, 杨慧群, 韩进朝. 改善发射药力学性能方法研究进展[J]. 化工新型材料, 2019, 47(7): 50-59.

WANG Y Q, YANG H Q, HAN J C. Study progress in method for improving the mechanical property of gun propellant [J]. New Chemical Materials, 2019, 47(7): 50-59.(in Chinese)

[4] 杨均匀, 袁亚雄, 张小兵. 发射药破碎对火炮射击安全性影响的研究综述[J]. 弹道学报, 1999, 11(4): 92-96.

YANG J Y, YUAN Y X, ZHANG X B. Research survey of the effect of grain fracture on the fire safety in solid propellant gun [J]. Journal of Ballistics, 1999, 11(4): 92-96.(in Chinese)

[5] 徐劲祥. 发射装药挤压破碎对燃烧规律的影响[J]. 火炸药学报, 2007, 30(3):69-71.

XU J X. Effect of extrusion and fracture of gun propellant charge on combustion behavior[J]. Chinese Journal of Explosives and Propellants, 2007, 30(3):69-71.(in Chinese)

[6] 陈涛, 芮筱亭, 贠来峰, 等. 发射药床动态挤压破碎模拟研究[J]. 南京理工大学学报, 2006, 30(4):467-471.

CHEN T, RUI X T, YUN L F, et al. Dynamic extrusion and fracture simulation of propellant charge bed [J]. Journal of Nanjing University of Science and Technology, 2006, 30(4):467-471.(in Chinese)

[7] 姜世平, 黎超. 火炮发射药床冲击破碎动力学仿真研究[J]. 弹道学报, 2019, 31(3):41-45.

JIANG S P, LI C. Dynamic simulation of fragmentation of gun propellant bed under impact load [J]. Journal of Ballistics, 2019, 31(3):41-45.(in Chinese)

[8] 姜世平, 芮筱亭, 洪俊, 等. 发射药床冲击破碎过程的数值模拟 [J]. 固体力学学报, 2011, 32(4):419-425.

JIANG S P, RUI X T, HONG J, et al. Simulation of fragmentation process of propellant ben under impact load [J]. Chinese Journal of Solid Mechanics, 2011, 32(4):419-425.(in Chinese)

[9] 洪俊, 芮筱亭. 发射药粒冲击破碎动力学仿真[J]. 弹道学报, 2010, 22(1):61-64.

HONG J, RUI X T. Dynamic simulation for impact and fracture of propellant grain [J]. Journal of Ballistics, 2010, 22(1):61-64.(in Chinese)

[10] 韩屹湛. 多孔发射药力学特性实验研究与数值仿真[D]. 南京：南京理工大学，2016.

HAN Y Z.Experimental study and numerical simulation on the mechanics characteristic of multi-perforated propellant [D]. Nanjing:Nanjing University of Science and Technology， 2016.(in Chinese)

[11] PAN B, QIAN K M, XIE H M, et al. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review [J]. Measurement Science and Technology, 2009, 20(6):062001.

[12] HILD F, ROUX S. Digital image correlation: from displacement measurement to identification of elastic properties - a review [J]. Strain, 2006, 42(2):69-80.

[13] 段淇元, 宫文然, 郭保桥, 等. 高温数字图像相关方法中的制斑和图像处理技术[J]. 清华大学学报(自然科学版), 2019, 59(6): 425-431.

DUAN Q Y, GONG W R, GUO B Q, et al. Techniques of speckle fabrication and image processing for high temperature digital image correlation [J]. Journal of Tsinghua University (Science and Technology), 2019, 59(6): 425-431.(in Chinese)

[14] 易亚楠, 张小娟, 马少鹏, 等. 基于数字图像相关方法的核石墨力学参数测量[J]. 核动力工程, 2019, 40(3):61-65.

YI Y N, ZHANG X J, MA S P, et al. Parameters measurement of nuclear graphite based on digital image correlation [J]. Nuclear Power Engineering, 2019, 40(3): 61-65.(in Chinese)

[15] 王礼立, PLUVINAGE G, LABIBES K. 冲击载荷下高聚物动态本构关系对粘弹性波传播特性的影响[J]. 宁波大学学报, 1995, 18(3):30-57.

WANG L L, PLUVINAGE G, LABIBES K. The influence of dynamic constitutive relations of polymers at impact loading on the viscoelastic wave propagation character [J]. Journal of Ningbo University, 1995, 18(3):30-57.(in Chinese)

[16] 施绍裘, 喻炳, 王礼立. PP/PA共混高聚物在高应变率下的热粘弹性本构关系和时温等效性[J]. 爆炸与冲击, 2007, 27(3):210-216.

SHI S Q, YU B, WANG L L. Thermoviscoelastic constitutive equation of PP/PA blends and its rate-temperature equivalence relation at high strain rates [J]. Explosion and Shock Waves, 2007, 27(3):210-216.(in Chinese)