两路微振动信号的光纤F-P腔干涉测量
赵 忖,刘径舟
(1.东北石油大学秦皇岛校区,河北 秦皇岛 066004;2.大庆油田有限责任公司,黑龙江 大庆 163000)
1 引 言
精细加工技术飞速发展,使得物体微位移和微振动测量日益受到重视。高分辨率空间遥感卫星的研制、航天器扰动预测等,均需要精确采集振源数据,基于FFT变换的动态频域标定方法,测出六维广义力的线性度在0.1 % FS以内[1]。卫星姿轨控中,微振动检测系统三轴线性度7.393pT·Hz-1/2[2]。微振动还可用于地下连接墙接缝刚度和强度测试[3],雕刻机主轴共振的各阶振型分析等[4]。因微振动形式复杂,振动多向且幅度小,频率分布范围广,故精确测量难度大。光学测量技术精度高,抗电磁干扰能力强,动态范围大,能在易燃易爆环境下可靠运行,是一种重要的非接触式无损测量的技术[5-8],在微位移和微振动测量中占据了主导地位。基于激光自混合干涉的高精度角度测量,在±0.4°角度范围内测量精度可达(±3.1×10-3)[9]。基于激光自混合散斑干涉的微小流量检测,相对误差小于1.13 %[10]。基于激光多重反馈自混合干涉的振动测量,在管道泄漏点定位中,误差小于5 %[11]。光纤自混合型多普勒测速仪的研制成功[12],推动了光纤自混合干涉测量技术的发展与应用[13-15]。光纤F-P腔传感器由两块平行的玻璃板组成,其相对内表面都具有高反射率。作为一种结构简单的多光束干涉仪,引发了研究者极大兴趣,新型光纤F-P腔传感器不断涌现[16-19]。为了使用一套光纤F-P腔系统同时测量两个目标,首先利用分光镜对激光器发射光进行分离,然后采集两个待测目标的微振动信息,反馈后形成光纤F-P腔干涉信号。再进行光电转换,对电信号进行多次取包络分解,通过快速傅里叶变换获取基频和主频,基于主频阶次计算出两路微振动信号幅值。
2 两路微振动信号的光纤F-P腔干涉测量原理与实验
两路微振动信号的光纤F-P腔干涉测量原理如图1所示。F-P内腔的两个端面为R1和R2,长度为LD,待测物体为M1和M2。激光器发出的光波传送到R2镜时,一部分反射回内腔,一部分由内及外透射到外腔,再由分光镜分成两部分,分别投射到两个物体表面。携带微振动信息的两路光波反射回外腔,又传送至R2镜形成由外而内的透射。这样内腔既含有透射回的两路光波,也有原反射光波,耦合后形成干涉信号,最终传送到光电探测器PD。弱反馈状态下,两路干涉信号光功率等于两个单路分别干涉时的光功率之和[20]。

图1 两路微振动信号的光纤F-P干涉测量原理
两路微振动信号的光纤F-P腔干涉测量系统如图2所示。为了减小由实验环境引起的误差,将上述所有实验设备放置在气浮光学隔振平台上。

图2 两路微振动信号的光纤F-P腔干涉测量实验系统
分布式反馈(Distributed Feedback,DFB)激光器光谱纯度高,与传统的半导体激光器相比,半导体增益区内置了相移光栅结构。DFB激光器选型Thorlabs,S3FC1550;2×2单模光纤耦合器选型THORLABS,10202A-50-FC;准直器选型F220FC-1550;光电探测器(Photodetector,PD)选型PDA10CS-EC;数据采集卡选用NI公司的USB-4431;锆钛酸铅(PbZrxTi1-xO3,PZT)驱动器和陶瓷片配套选用,后者型号分别为P-752和P-753。为了保证DFB激光器输出波长以及功率的稳定,增加了温控器件,选型LTC100-B。
对两路微振动信号进行测量时,DFB激光器发出波长λ0为1550 nm的单纵模光,选取反馈因子C=0.5,采用正弦信号,设定PZT1频率60 Hz,振幅1 μm;PZT2频率0.5 Hz,振幅2 μm。采集到的信号经去噪预处理如图3所示,小窗口系局部放大图。
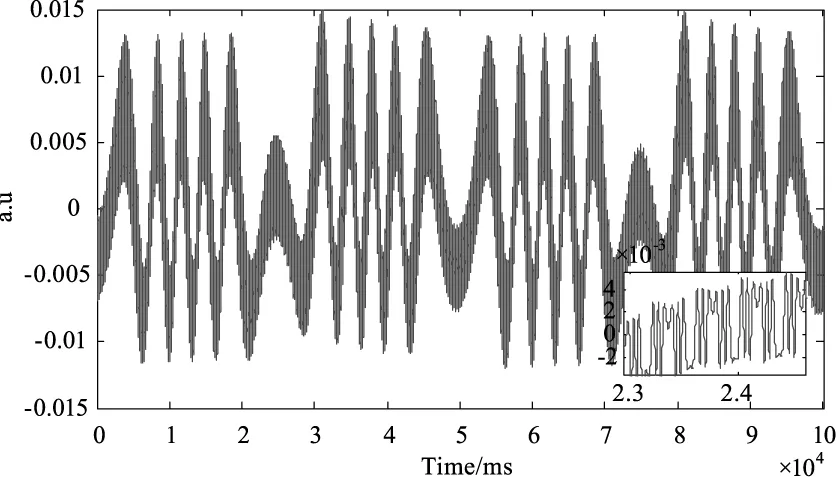
图3 去噪处理后的两路反馈光纤F-P腔干涉信号
3 两路反馈光纤F-P腔干涉信号的分解
依据弱反馈状态下两路干涉信号叠加原理,对图3所示波形采用取上下包络方式进行分解[21],可将原始信号P(t)分解为较低频率的Pdi(t)信号和较高频率的Pgao(t)信号,如图4所示。
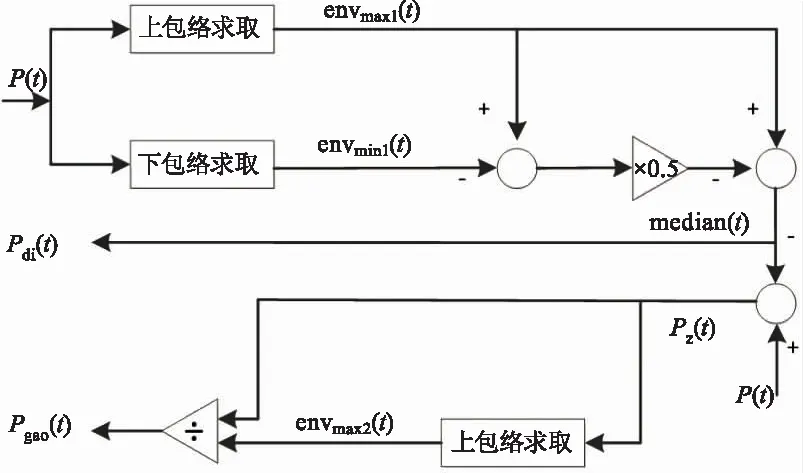
图4 两路反馈光纤F-P腔干涉信号分解流程
对图3的上下包络采用局部最大值检测和局部最小值检测方法获得。通过式(1)求取中值median(t),作为一路低频信号Pdi(t),如图5所示。图5中b线为上包络信号,c线为下包络信号,a线为中值信号。
median(t)=envmax1(t)-[envmax1(t)-envmin1(t)]/2
(1)
式中,envmax1(t)为F-P腔干涉信号上包络;envmin1(t)为F-P腔干涉信号下包络。

图5 两路反馈光纤F-P腔干涉信号上下包络及中值
依据图4,通过式(2)得到一个新的信号Pz(t),如图6(a)所示,观察其特点,称之为过零信号。
Pz(t)=P(t)-median(t)
(2)
对过零信号再取一次上包络,记为envmax2(t)。根据式(3),结合图4,可图3分解出一路高频信号,如图6(c)所示。
Pgao(t)=Pz(t)/envmax2(t)
(3)

图6 过零信号、过零信号的上包络及分离出的较高频率的一路信号
对图3使用EMD算法,也能分解出高、低频信号[22]。与之比较,该方法解决了高频信号残留部分低频成分的问题。
4 两路微振动信号幅值计算
从光纤F-P腔干涉信号分离出高、低频信号后,通过快速傅里叶变换得到频谱图,进而获得基频fb和主频fd1。根据式(4)可计算出主频阶次nd,按照式(5)可计算出A,即为PZT的振幅[5]。光纤F-P腔干涉信号分离出的低频信号计算出的A对应PZT2的振幅,高频信号计算出的A对应PZT1的振幅。
(4)
(5)
对图6(b)所示低频信号进行快速傅里叶变换,得到频谱如图7所示,从中提取出基频fb为0.4612 Hz,主频fd1为6.457 Hz。综合式(4)、(5),计算出PZT2的振幅为1.9736 μm,与实际2 μm的振幅相比,误差为1.32 % 。
对图6(c)所示高频信号进行快速傅里叶变换,得到频谱如图8所示,从中提取出基频fb为60.42 Hz,主频fd1为423.7 Hz。同理计算出PZT1的振幅为1.0663 μm,与实际1 μm的振幅相比,误差为6.63 %。
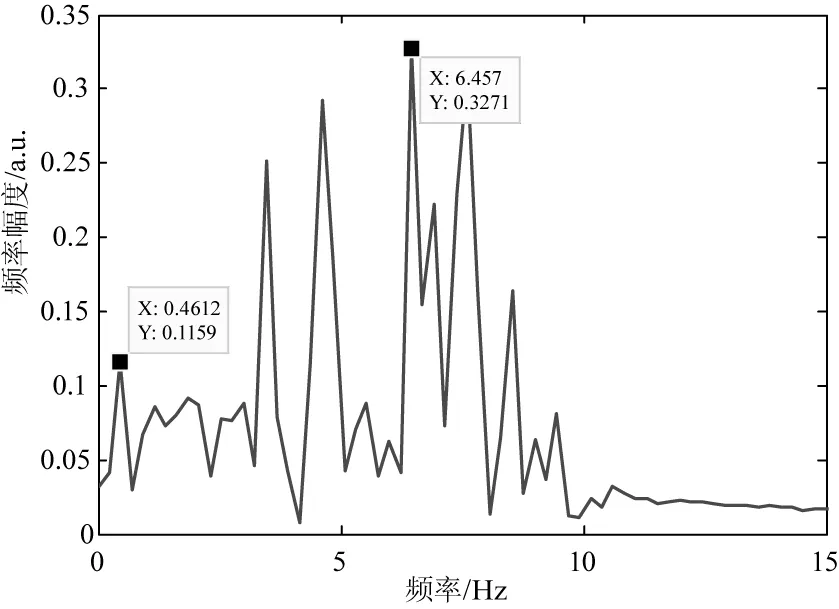
图7 两路反馈光纤F-P腔干涉信号分解出低频信号频谱
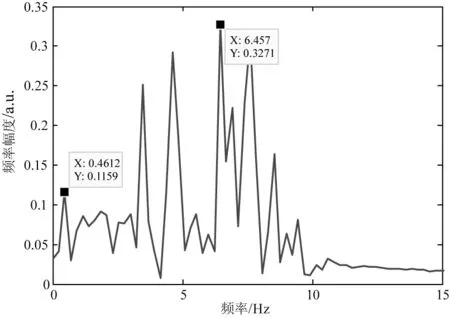
图8 两路反馈光纤F-P腔干涉信号分解出低频信号频谱
5 结 论
两路反馈光纤F-P腔混合干涉系统能够同时对两路微振动信号进行测量,结果表明:
(1)使用一套光纤F-P腔干涉系统可同时对两个目标进行测量,结构简单,稳定性好,抗干扰能力强。
(2)对两路反馈光纤F-P腔干涉信号进行取包络分解,能够快速、准确的分离出待测目标微振动幅度。
(3)该方法解决了EMD算法分离出的高频信号残留部分低频成分的问题。