高地温隧道施工过程气温-时间数学关系研究

胡 政，杨 松，艾祖斌，郭维祥，陈全胜

(1.中国电建集团贵阳勘测设计研究院有限公司,贵州 贵阳 550081；2.中电建路桥集团有限公司,北京 100048)

0 引言

在我国西南地区进行工程建设，面临诸多挑战，如地形地质条件复杂、地震震害、高地应力、高地温、高压涌水等[1]。西南云南省地热资源丰富[2-3]，交通、水电及国防等领域的地下工程建设将面临更多的高地温问题。高地温区的地下工程建设存在施工环境恶劣、机械效率低、施工安全风险高(热水害、高温、有毒有害气体等)、结构安全性及耐久性、投资成本大幅增加等问题[4-8]。

施工区域环境温度(即洞内掌子面10 m范围的气温)直接关系到隧道施工作业人员安全与健康、施工降温方案等，目前关于高地温隧道施工过程各环节(打钻、爆破、出渣、初支)气温随时间变化的研究尚为少见，且针对性不强。陈乾阳等(2019)[9]利用Fluent数值计算软件，分析了不同通风速度、不同通风气温下隧道内温度场的分布，探讨了较优通风参数。高焱等(2018)[10]以祁连山隧道为研究对象，建立非稳态的隧道温度场模型，采用变量控制法探讨不同时间、距离以及有无保温层条件下寒区隧道洞内空气和围岩温度场的变化规律。鲁华伟(2017)[11]建立拉法山隧道施工通风模型，采用数值模拟的方法对风管漏风和围岩温度对隧道施工段洞内气温变化规律进行研究。李铁根(2013)[12]根据温度场的控制微分方程及有限元公式，通过理论计算及数值模拟分析，分别得到在同样的时间周期内相同气温变化对隧道调温圈大小的影响。张先军(2005)[13]分析了昆仑山隧道洞内气温、地温及隔热层内外侧温度分布特征，对多年冻土区隧道工程建设及冻害防治有一定的指导意义。仇玉良等(2004)[14]研究隧道位置地层温度、洞内风速变化、外界气温变化等因素影响下，隧道内自然风速及洞内气温的变化范围和变化规律。夏丰勇等(2015)[15]针对单坡隧道左右线通风负荷不均衡的问题,提出了双洞互补式通风方式，均衡了左右线隧道风量,降低能耗，节约了初期投资。现有研究主要是通过数值模拟或间断性温度测试进行隧道整体的温度场研究，未有针对施工区域环境温度进行连续性监测并建立一个完整施工循环各施工环节气温随时间的变化关系的研究。

本研究以云南省红河州建水(个旧)至元阳高速公路工程在建尼格高地温隧道为研究对象，对隧道出口花岗岩段(里程46 754～46 737m)施工环境的气温进行了5个完整的施工循环的连续监测，共采集了2 200个气温&时间值，分析各施工环节(打钻、爆破、围岩散热、出渣)的气温随时间的变化特征，将一个完整施工循环过程的气温变化过程划分为4个变化阶段，并建立了施工过程的气温-时间数学关系表达式，为针对性的施工降温措施提供依据。

1 工程背景

红河州建水(个旧)至元阳高速公路为云南省“五纵五横一边两环二十联”中曲靖至呈贡、通海、建水、元阳的重要组成部分，尼格隧道位于该高速公路个旧至元阳段，隧道全长3.3 km，最大埋深640 m，施工采用进、出口双向双洞施工。隧道施工过程中出现高岩温、高水温、有毒有害气体、隧道涌水、岩爆等问题，最高岩温达88.8 ℃，为目前我国最高地温公路隧道，施工风险高，施工难度大。

通过引进多臂钻替换传统人工作业、设置20 t制冰系统制冰、增加轴流风机加强通风、引进耐高温雷管替换传统雷管、掌子面附近设计空调房轮流降温、雾炮机喷淋洒水等6项措施改善隧道内高温施工环境，通过配备正压式空气呼吸器、四合一气体检测仪、压缩氧气自救器等8项有毒有害气体检测和防护设备保证施工作业人员的身体健康，工程历时2 a，于2020年6月22日实现双幅贯通。本工程案例颇为典型，具有重要借鉴和类比意义。

出现高地温后，对各类地温进行了持续性测试，目前共采集地温数据超过25万组[16]，并预埋了近百套温度计、应力计、应变计等元件。对隧道出水、周边温泉水、地表水等取样进行了大量水化分析试验(阴阳离子、氢氧同位素、锶同位素等)，对隧道围岩取样进行了热力学参数、岩石衰变生热、微量元素及XRD谱等检测，编制了隧道高地温地质成因、设计、施工、管理等多个专项报告。

隧道纵剖面及地温整体情况如图1所示。隧道穿越依次穿越三叠系中统个旧组(T2g)灰岩、燕山期侵入花岗岩(γ53(a))。灰岩段主要表现为高水温，最大涌水量9～12 L/s，最高水温63.4 ℃，最高气温达41 ℃；花岗岩段主要表现为高岩温，最高温度达88.8 ℃，最高气温达56.4 ℃。隧道干燥无出水，围岩坚硬程度及完整程度均较好。

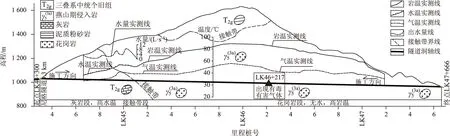
图1 尼格隧道纵剖面及地温实测简图Fig.1 Schematic diagram of measuring longitudinal section and ground temperature of Nige Tunnel

2 测温装置设计

2.1 测量装置

为了测量隧道各施工环节的施工环境(掌子面附近10～20 m范围)气温变化特征，需设计一套自动温度记录装置。

气温测量装置设计如下(如图2所示)：(1)测温仪选择，选用温度自记仪(98 mm×49 mm×25 mm)，测量范围-50～100 ℃(测量精度±0.3 ℃)，记录长度30 000 点，测量前进行仪器标定。(2)保护装置设计，隧道施工过程的爆破飞石、震动、洒水等可能造成测温仪损坏、失效等，需设置保护装置，可用钢板(厚约1～3 mm)焊接一保护盒，在保护盒底部预留一测温探头出口，并在下部边缘设置挡水板。(3)测温装置的设置位置，为了不影响隧道施工交叉作业，测温装置一般设置在距掌子面5～8 m 处的隧道边墙，高度一般3～5 m，由一长约1～2 m铁质挑杆悬挑于隧道边墙，挑杆须嵌入边墙岩体一定深度(一般20 cm)。

2.2 测量方法

首先设定温度记录间隔时长，一个施工循环一般需要9～12 h，温度记录间隔时长设置为2 min，可测得270～360个气温值；为了保证各施工循环测量装置距掌子面距离相同，每一个施工循环完成后测温装置往掌子面方向前移3～4 m(一个施工循环的进尺)。每一施工循环的施工环节依次为：打钻(炮眼)、爆破、出渣、初支(本段围岩条件好，围岩自稳性好，初支环节忽略)。在测温过程中可能存在施工机械作业、通风、洒水以及洞外气流等影响因素。

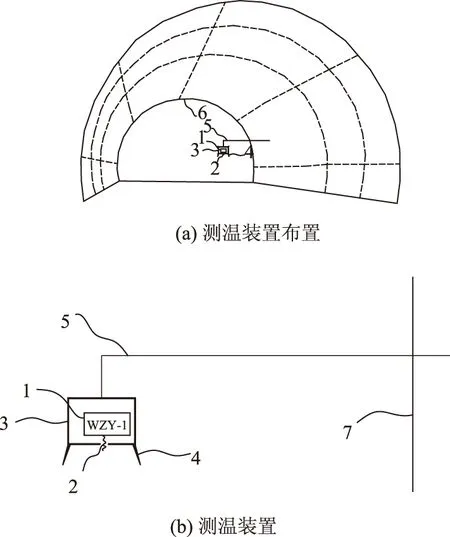
1—测温仪(温度自记仪);2—测温仪探头;3—保护装置;4—挡水板;5—挑杆;6—隧道掌子面;7—隧道边墙图2 各施工环节温度测试设计Fig.2 Design of temperature testing for each construction link

3 气温测试成果

本次对隧道施工区域(掌子面附近)的气温进行了6个施工循环(其中5个完整的施工循环)的连续测试，测试时长共计约74 h，共采集了约2 200个气温值，成果资料整理如图3所示，测试洞段的主要施工工况如表1所示。可以看出，测试段最高气温达50.5 ℃，最低气温39.6 ℃；各施工循环气温曲线呈现下降(打钻施工环节)-骤升(爆破施工环节)、上升(围岩散热)-缓降(出渣施工环节)的特征；打钻环节主要受通风、洒水等确定性因素影响，各施工循环变化趋势相近，气温下降3～7 ℃；爆破施工环节在短时间内气温出现骤升，上升值为4～6 ℃，但持续时间短；爆破后的围岩散热亦导致气温出现骤升，骤升速率较第2阶段小，但持续时间长；出渣施工环节气温值变化较为复杂，且出现多处异常高值，分析原因为：该环节初始阶段受爆破余热、围岩散热影响，气温出现一定的上升，通风、洒水排烟(尘)等降温措施后气温有所下降，但受出渣车辆及挖机等机械作业影响，气温出现多处异常高值(2～3 ℃)。

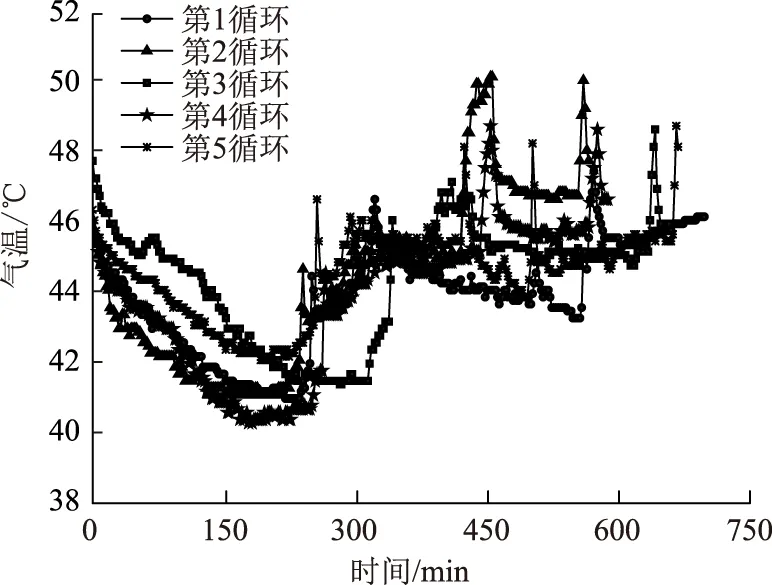
图3 各施工循环气温变化曲线Fig.3 Air temperature change curves of each construction cycle

4 施工过程气温-时间变化特征分析

4.1 气温随隧道里程、埋深及岩温的变化特征

将隧道岩温(新爆后)、气温的测量成果整理如图4所示，隧道从47 100 m里程施工至46 000 m里程，隧道埋深从167 m增至635 m，岩温从52.6 ℃上升至88 ℃，气温从35.2 ℃上升至56.4 ℃，岩温与气温之差一般为25～30 ℃；岩温与气温随隧道埋深及进深增加呈现上升趋势；气温升高的主要原因为岩温的升高，气温值的大小与岩温密切相关。

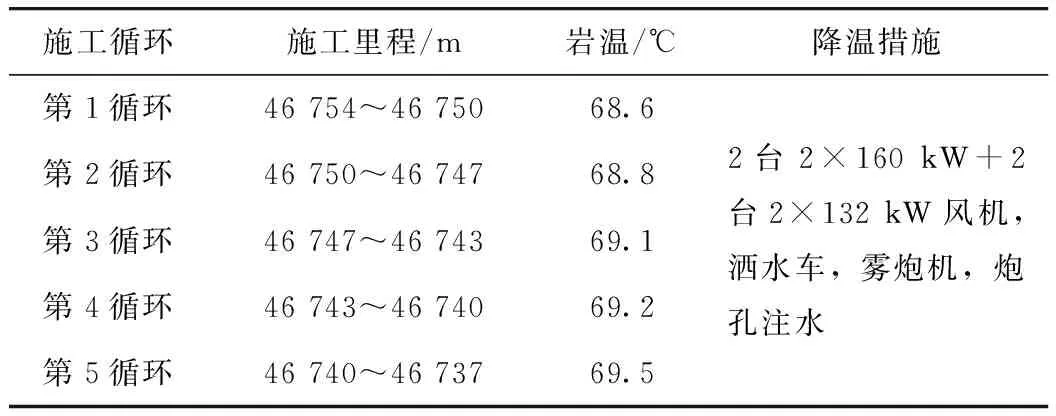
表1 气温测量洞段的主要施工工况

图4 隧道岩温、气温、埋深随隧道里程的变化曲线Fig.4 Curves of rock temperature, air temperature and buried depth varying with tunnel mileage

用y=ax+b拟合隧道气温(爆破后)与岩温的变化关系，如图5所示，拟合结果和测量数据相关性较高，该阶段气温随岩温呈现线性递增的趋势，公式为y=0.616x-0.115。

图5 隧道气温-岩温的线性拟合Fig.5 Linear fitting of tunnel air temperature and rock temperature

4.2 施工区域各施工环节气温随时间变化特征

从图3可以看出，气温随时间的变化可划分为4个变化阶段：下降阶段(第1阶段)，骤升阶段(第2阶段)，上升阶段(第3阶段)，缓降阶段(第4阶段)。

第1阶段：对应打钻(炮眼)施工环节，受通风、洒水等因素影响，气温随时间呈现下降的趋势，下降值为3～6 ℃，下降率约6～8%。

用y=ax+b拟合5个施工循环第1阶段的气温随时间的变化关系，如图6所示，拟合结果和测量数据相关性较高，该阶段气温随时间(打钻施工环节)呈现线性递减的趋势，公式为

y=(-0.188～-0.226)x+(44.02～46.77)。

(1)

第2阶段：对应装药及爆破施工环节，受炮孔注水降温等因素影响，初始阶段气温相对稳定，爆破后气温呈现骤升的趋势，上升值为4～6 ℃，上升率约10～12%。该过程亦比较符合Boltzmann曲线特征，该函数在拟合温度变化、沉降变化等方面较为合理[17-18]。

图6 第1阶段气温-时间的线性拟合Fig.6 Linear fitting of air temperature and time in stage 1

用Boltzmann函数拟合5个施工循环第2阶段的气温随时间的变化关系，Boltzmann函数为

(2)

式中，A1，A2分别为气温极低值、极高值；x0为y=(A1+A2)/2时的x值，该值接近于爆破起爆时间；dx为(xmax-xmin)/20计算得到，该值的大小表征了气温骤升的快慢，dx值越小说明气温骤升越快，反之表明了气温骤升越慢。

第2阶段的气温随时间拟合曲线如图7所示，各参数如表2所示，拟合结果和测量数据相关性较高，公式为

(44.5～46.7)。

(3)

图7 第2阶段气温-时间的Boltzmann拟合曲线Fig.7 Boltzmann fitting curves of air temperature and time in stage 2

表2 第2阶段气温的Boltzmann拟合参数值

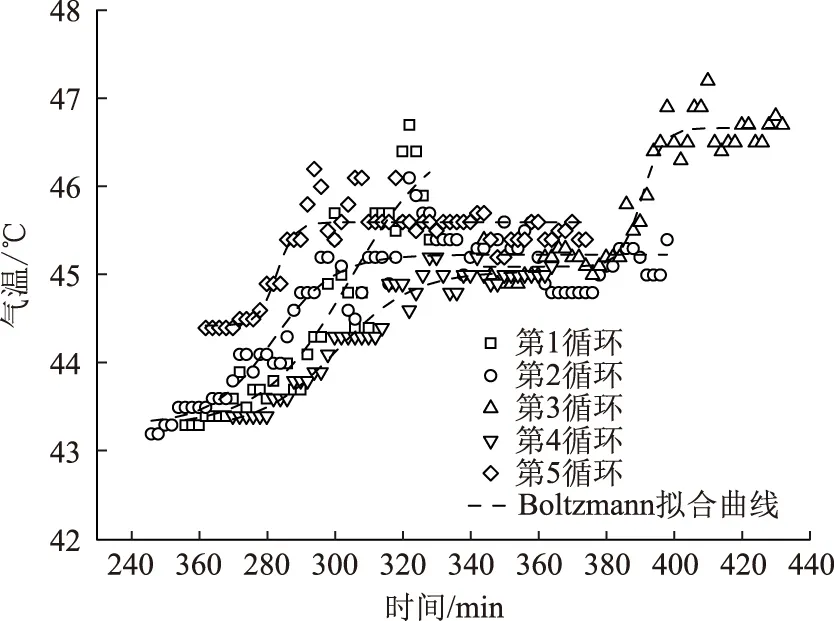
图8 第3阶段气温-时间的Boltzmann拟合曲线Fig.8 Boltzmann fitting curves of air temperature and time in stage 3

第3阶段：爆破后温度骤升，但持续时间较短，并出现骤降，该阶段为气温骤降一定值后，由于揭露出的新鲜高温围岩散热致使气温出现快速上升，上升值为1～3 ℃，上升率约4%～5%，上升速度为先快后慢，该过程亦比较符合Boltzmann函数曲线特征。用Boltzmann函数拟合5个施工循环第3阶段的气温随时间的变化关系，如图8所示，各参数如表3所示，拟合结果和测量数据相关性较高，公式为

(45.0～46.7)。

(4)

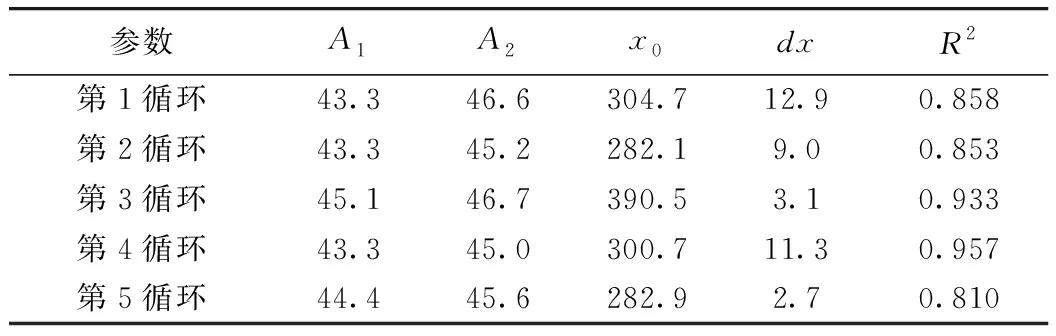
表3 第3阶段气温的Boltzmann拟合参数值

第4阶段：对应出渣施工环节，初始阶段受通风、洒水排烟(尘)等因素影响，整体呈现缓降趋势，下降率约1%～2%；中后阶段受出渣车辆及挖机等机械作业影响，气温出现多处异常高值(骤升2～3 ℃)。

剔除受出渣车辆等机械作业影响的异常值后，用y=ax+b拟合5个施工循环第4阶段的气温随时间的变化关系，如图9所示。由于受机械作业影响较大，拟合结果和测量数据相关性偏低，该阶段气温随时间呈现线性递减的趋势，公式为

y=(-0.002 44～-0.018 1)x+(46.50～51.59)。

(5)

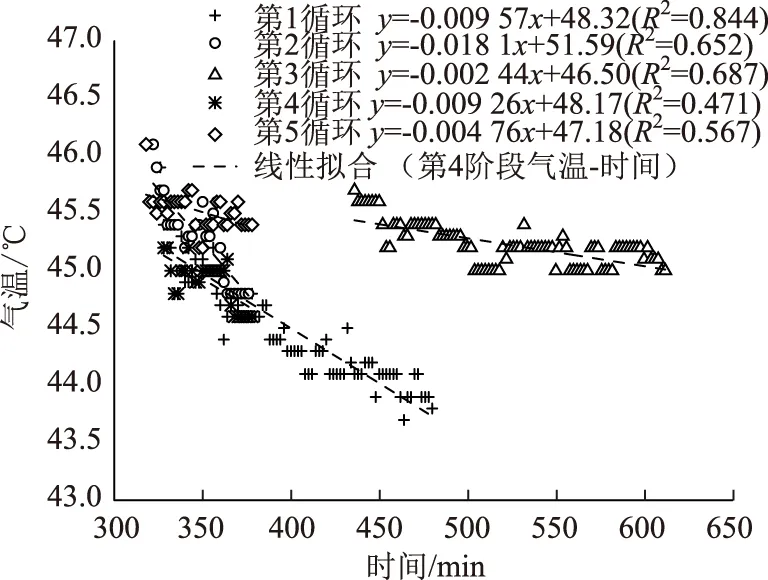
图9 第4阶段气温-时间的线性拟合曲线Fig.9 Linear fitting curves of air temperature and time in stage 4

5 施工过程气温-时间数学关系

5.1 各阶段气温变化对比分析

第1阶段、第4阶段气温随时间呈现下降趋势，前文对气温-时间进行了线性拟合，对比分析拟合所得参数a、b值，见图10，第1阶段参数a的绝对值较第4阶段大，即第1阶段拟合线的斜率较大，气温随时间下降较快；第4阶段的参数b值较第1阶段大，主要是因为第3阶段围岩散热致使气温上升，达到高值。

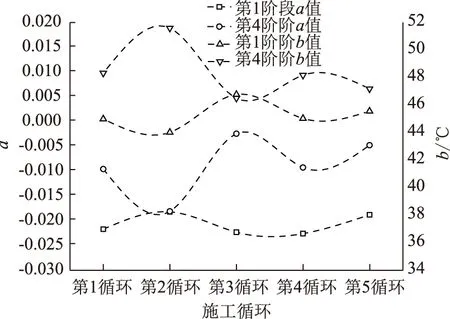
图10 线性拟合参数a、b对比分析曲线Fig.10 Comparison analysis curves of linear fitting parameters a and b

第2阶段、第3阶段气温随时间呈现骤升，具有较为明显的Boltzmann函数特征，对气温-时间进行了Boltzmann拟合，对比分析拟合所得参数A1，A2值及dx值，如图11、图12所示。第3阶段的A1，A2值均较第2阶段大，主要是因为第2阶段爆破致使气温骤升，虽然其持续时间较短，并出现一定骤降，但爆破出的新的高温围岩立即对气体进行了增温。第2阶段的dx值较第3阶段小，说明爆破过程气温骤升速度较围岩散热致使气温骤升的速率大，但由于爆破能量为瞬间释放，持续时间短，出现一定的骤降，而新的高温围岩散热增温持续时间较长，致使隧道气温在第3阶段达到高值。

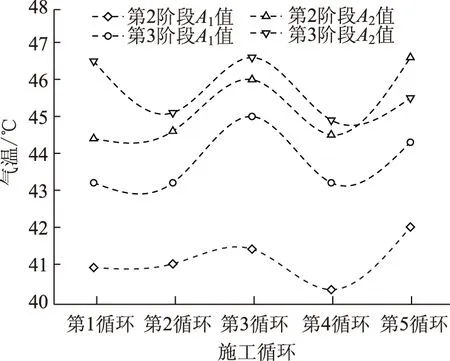
图11 Boltzmann拟合参数A1,A2对比分析曲线Fig.11 Comparison analysis curves of Boltzmann fitting parameters A1 and A2

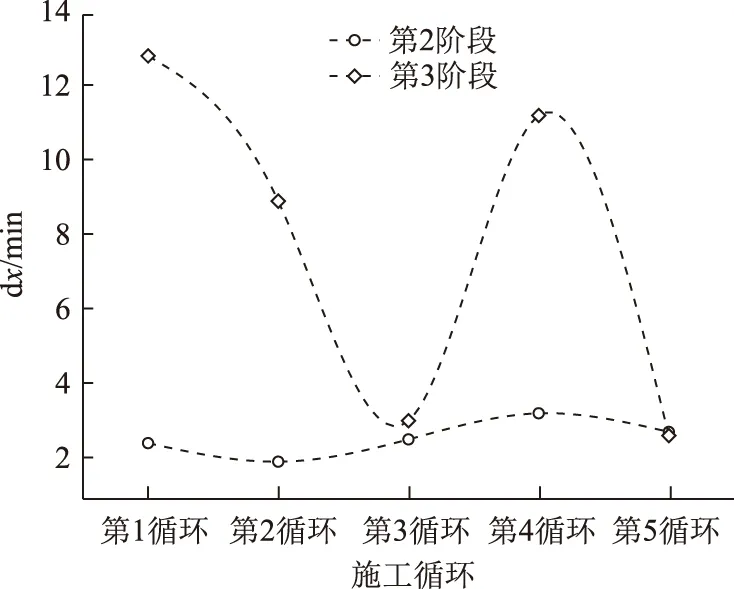
图12 Boltzmann拟合参数dx对比分析曲线Fig.12 Comparison analysis curves of Boltzmann fitting parameter dx

5.2 施工过程气温-时间的数学模型

综合以上分析，可以得到施工过程(一个施工循环)的气温-时间曲线模型(如图13所示)，气温随时间的变化呈现4个阶段的特征。第1阶段(t0～t1)，为打钻施工环节，受通风、洒水等因素影响，气温随时间呈现线性递减趋势；第2阶段(t1～t2)，为爆破施工环节，气温随时间呈现骤升趋势，可用Boltzmann较为准确地描述气温-时间关系，该过程持续时间短，气温骤升后出现一定的骤降；第3阶段(t2～t3)，为爆破后新揭露的高温围岩散热过程，亦可用Boltzmann较为准确地描述气温-时间关系；第4阶段(t3～t4)，为出渣施工环节，该过程受机械作业影响较为明显，气温出现多处异常高值，剔除异常值后，气温随时间呈现线性缓降趋势。

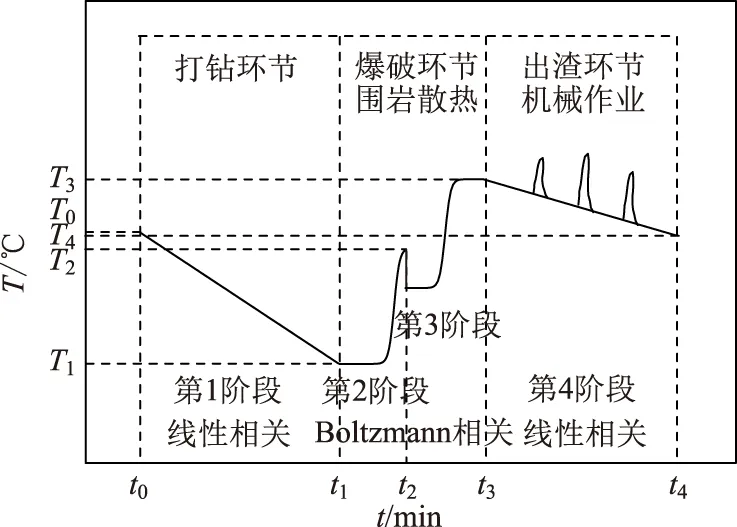
图13 施工过程气温-时间关系模型Fig.13 Model of relationship between air temperature and time in construction process

忽略机械作业对气温的影响，隧道施工过程的气温-时间数学关系可表达为

(6)

式中，T为隧道施工环境气温；t为施工时间；a(1)，b(1)分别为第1阶段线性函数的斜率、截距；A1(2)，A2(2)分别为第2阶段Boltzmann函数的气温极低值、极高值；x0(2)为第2阶段Boltzmann函数y=(A1(2)+A2(2))/2时的x值，接近于爆破起爆时间；A1(3)，A2(3)分别为第3阶段Boltzmann函数的气温极低值、极高值；x0(3)为第3阶段Boltzmann函数y=(A1(3)+A2(3))/2时的x值，为爆破后短时间；dx(2)，dx(3)分别为第2、第3阶段表征气温骤升的快慢物理量，按(x(2、3)max-x(2、3)min)/20计算得到。

施工过程的气温随各施工环节呈现不同的变化趋势，各阶段具有不同的数学关系式，但气温值受岩温影响大(岩温可视作气温的主要热源)，新爆破的高温围岩岩温与气温具有较好的线性关系，公式如下：

T(A2(3))=a0T岩+b0。

(7)

6 结论

(1)本研究实测了5个完整施工循环的2 200多个气温&时间值，研究了气温随时间变化特征，建立了施工区域各施工环节气温随时间的数学关系，对同类高地温隧道施工通风、降温等具有指导意义。

(2)将施工过程的气温变化划分为4个阶段，并建立了施工过程气温-时间的数学关系式。第1阶段气温随时间呈现线性下降趋势，下降率约6%～8%；第2阶段气温随时间呈现骤升趋势，上升率约10%～12%，第3阶段气温随时间呈现快速上升趋势，上升率约4%～5%，第2阶段、第3阶段用Boltzmann函数能比较准确地描述其气温随时间的变化关系；第4阶段气温随时间呈现线性缓降趋势，下降率约1～2%，但受机械作业影响，气温出现多处异常高值。

(3)气温升高主要原因为岩温的升高，新爆破的高温围岩岩温与气温具有较好的线性关系。爆破过程气温骤升，但持续时间短。施工降温应重点关注爆破后短时间内的新爆围岩散热，针对性采取降温措施，同时应关注洞内机械作业导致气温升高。