考虑相邻跑道干扰的多目标进离场航班排序优化模型

吴 维, 魏 明*, 叶志坚, 孙 博

(1.中国民航大学民航航班广域监视与安全管控技术重点实验室, 天津 300300； 2.中国民航大学空中交通管理学院, 天津 300300)

由于各个航班的航空器型号(决定尾流)和跑道运行模式对间隔影响差异,当机场的飞机流量迅速增加时,如果不通过进离场航班的排序与调度(flight arrivals and departures scheduling problems,FADSP),必然出现航空器在终端区的大面积拥堵与延误问题。与传统排序问题不同,随着航班运行环境和运行规则的变化,FADSP具有独特的运行特征,具体表现在:①新运行标准和安全间隔的发生变化；②多跑道混合运行模式并存；③涉及多种竞争性资源限制,尤其管制工作负荷带来影响。该问题是一个非确定性多项式(non-deterministic polynomial,NP-hard)难题,为此,很多学者针对该问题进行了研究以提升机场中跑道资源的有效利用,提升运行效率。

目前,针对FADSP的中外研究按照跑道使用主要划分为单、多跑道,进场、离场以及进离场混合；目标函数分为:单、多目标；约束条件分为:确定和不确定。张兆宁等[1-2]研究一类多跑道运行模式、替代航路的FADSP,以减航班延误为目标；Lieder等[3]研究了不同运行模式下(相关和独立运行)的多跑道FADSP；张启钱等[4]根据新的尾流间隔标准和多跑道属性差异构建一类FADSP,追求管制员工作负荷和产生延误成本最小；Bae等[5]研究了一类离场航班的多目标FADSP,引入饱和度以降低排序方案可能引起的总延误成本增加；Sureshkumar等[6]针对不同跑道构建FADSP的动态规划模型,平衡机场容量和航班延误之间关系；Sölveling等[7]构建了FADSP的两阶段随机规划模型；张军峰等[8]考虑管制运行约束、跑道容量和航迹预测,研究不同时间窗的进场FADSP；Sam[9]等研究了繁忙机场进离场动态优化的多目标FADSP；戴喜妹等[10]、周雨凡等[11]探讨了不确定因素引起的交通量猛增下的FADSP；Faye[12]研究综合考虑着陆航空器着陆时间、跑道可用性和间隔标准的FADSP; 张建同等[13]和张军峰等[[14]分别探讨了基于优先级和复合分派规则的FADSP；王莉莉等[15]、马园园等[16]和张军峰等[17]研究了多机场协同下的FADSP。在算法设计方面,针对大规模的规划问题求解主要采用滚动规划时间窗启发式方法[1,3-4],动态规划方法[2,12]、分支定界算法[6-8]、近似启发式算法[5,9,14-15]、蚁群算法[13]、遗传算法[10-11,16]、模拟退火[17]。

综上可知,现有研究主要不足在于:①现有FADSP均是假设航班的进离场跑道固定已知,较少涉及航班的不同跑道分配方案对FADSP的影响；②现有FADSP忽略了相邻跑道距离较近时,可能导致两个跑道无法同时进行航空器进离场的影响；③现有FADSP缺少分析管制员工作负荷导致跑道容量限制给排序结果带来的影响以及不同类型机型对跑道占用时间的影响。为此,研究一类考虑相邻跑道干扰的多目标FADSP,以航班延误和跑道利用效率为目标,综合考虑管制员可以调配每个时段进离场航空器总量限制。根据问题特征,设计该问题的NSGA-II,定义染色体编码、产生初始种群的启发式算法、遗传操作等。最后,结合某机场的实际数据,给出最佳排序方案并进行模型的参数灵敏度分析,从而验证模型和算法的有效性。

1 FADSP的多目标数学规划模型构建

1.1 问题描述

某机场在一段时间内有多个进离场航班,每个航班的计划时间、到达或离开、机型(尾流时间和跑道占用时间)提前可以预知,考虑管制员的最大管制负荷以及相邻跑道之间航班运行干扰性,将它们分配给一条或多条跑道依次进离场,确定全部航班的实际起飞或降落时间,同时追求跑道的利用效率最大化以及航班延误最少。根据问题特征,建立FADSP的多目标混合整数数学规划模型,寻找其Pareto最优解,从机场和乘客角度揭示不同优化方案对利益均衡性的影响。

不失一般性,研究的前提假设条件包括:①可以获取某段时间机场的进离场航班、机场跑道运行模式与管制负荷；②同一个航班不能同时被分配给两条跑道,一条跑道不能同时起飞或降落两个航班,不考虑复飞等起降特情；③航班进离场排序不受航班滑行排队的影响；④不考虑随机干扰影响航班不能正常起飞或降落。

1.2 数学模型

如表1所示,给出FADSP的相关符号变量定义,据此描述该数学模型的目标函数和约束条件,如下所示。

表1 变量定义和数学符号Table 1 Variable definition and symbols

1.2.1 目标函数

从机场和乘客角度,探讨航班进离场的延误时间、跑道作业分配之间最佳指派耦合关系,其中,机场方面关心跑道利用效率最高(空闲时间最少),用Z1表示；乘客方面关注航班总延误最少,用Z2表示。

(1)

(2)

1.2.2 约束条件

(1)航班指派跑道约束,即每个航班只能分配给一个跑道完成起降过程。

(3)

(2)跑道上航班起降顺序约束,即:每个航班进离场过程只被指派给一条跑道,同时一条跑道同一时间只能完成一个航班起降运行。

(4)

(5)

(3)避免子回路约束。

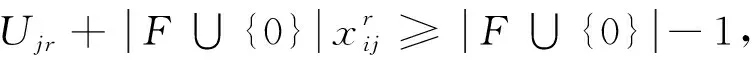
∀i,j∈F;∀r∈R

(6)

(4)某跑道完成相邻航班进离场运行的时间约束,即前续航班进离场运行的结束时间(即实际开始时间、跑道占用时间和尾流时间之和)不早于其后续航班进离场运行的开始时间。

(7)

(5)某航班进离场的计划和实际时间之间最大延误约束。

(8)

(6)相邻跑道运行模式的干扰约束,即如果相邻跑道之间距离较近采用相关运行模式,当某跑道的航班进离场运行时,相邻跑道的航班进离场运行必须提前或者滞后一定时间。

∀i,j∈F;∀r,k∈R

(9)

(7)基于管制工作负荷确定的各个时段跑道容量约束,包括每个时段的起飞、到达和总起飞降落航空器数量。

h∈H;∀r∈R

(10)

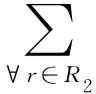
∀i∈F};h∈H;∀r∈R

(11)

0|∀i∈F};h∈H;∀r∈R

(12)

2 NSGA-II算法设计

非支配排序遗传算法(non-dominated sorted genetic algorithm-Ⅱ，NSGA-Ⅱ),其特征在于包含快速非支配排序、拥挤度和拥挤度比较三个算子,不仅降低了算法的复杂度,而且保持了种群的多样性。鉴于NSGA-Ⅱ的容易使用、原理简单等优点,已经被推广应用在交通、经济和工程等领域,是多目标进化基准算法之一。

借鉴NSGA-II求解FADSP的成熟思路[11,17],设计求解问题的启发式算法,给出了染色体编码方案,设计了产生初始种群构造算法,并给出了具体算法过程。

2.1 染色体编码

用二维向量U=(U1,U2)刻画FADSP的一个解,其中，U1=(u1,u2,…,uF),任意元素ui表示进离场航班i被分配的跑道号；在U2=(uF+1,uF+2,…,u2F),任意元素ui表示进离场航班i-F开始使用跑道的实际时间。例如,一个染色体 ={112222 7:30 7:40 7:30 7:40 7:40 7:50} 涉及6个航班(F1～F6)和3个跑道(R1～R3),将其可以解码为F1、F2被分配给R1,时间为7:30、7:40；F3、F4被分配给R2,时间为7:30、7:40；F5、F6被分配给R3,时间为7:40、7:50。

2.2 产生初始种群的启发式算法

当FADSP的多个航班被分配给同一或相关联跑道时,若这些航班的跑道占用时间窗重叠,其造成这个解不可行。因此,随机产生的染色体很难是可行个体。鉴于此,构造算法生成若干可行个体,组成初始种群,具体步骤如下。

步骤2对航班F″,设置可行初始跑道集合R，令i=1。

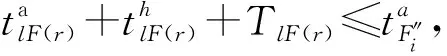
步骤4i=i+1。若i≤|F|,转至步骤3；否则,算法结束。

2.3 非劣排序和拥挤距离排序

2.3.1 非劣排序

步骤1设Sx表示某个解∃x∈P所支配的个体集合,nx表示某个解∃x∈P所支配的个体数量,令Sx=Ø和nx=0。对任意两个解∀q,x∈P,若q>x,则Sx=Sx∪{q}；否则,nx=nx+1。

步骤2产生的新一代种群为Q,当Q=Ø,令xrank=1和i=1,其中xrank为变量x的非支配排序值,满足F1={x|nx=0,∀x∈P}。

步骤3对任意∀x∈Fi的∀q∈Sx,令nq=nq-1。若nq=0,qrank=i+1且Q=Q∪{q}。

步骤4如果Q≠Ø,i=i+1且Fi=Q,转步骤3；否则,算法结束。

2.3.2 拥挤距离

2.3.3 选择算子

为使Pareto解均匀散布,对任意两个个体,当它们的非支配排序差异时,偏好序号低的个体,否则优先选取拥挤距离小的个体,即: ①i>j当且仅当irankD(xj)。

2.4 算法流程

步骤1设置算法参数,包括:染色体数N、迭代次数Niter以及遗传操作概率等。

步骤2随机产生第t=0代初始种群P0。

步骤3在第t代,对种群Rt内的若干个体进行选择、变异和交叉操作,生成下一代子代种群Qt,将其与父代种群合并,即Rt=Pt∪Qt。

步骤4对Rt的2N个体,计算它们的非支配序和拥挤距离,按照一定规则选取较好个体,当个体数量达到N时,将它们组成新种群Pt+1。

步骤5当t=t+1,若t≥Niter,算法迭代结束,输出结果；否则,返回步骤3。

3 算例分析

某机场在7:00—9:00期间有123个航班进离场,主要涉及轻、中型机两种机型,其中，进场72班次,离场51班次。根据全部航班的计划时间,图1刻画全部进离场航班占用跑道的数量随着时间变化而波动(差异较大),最少和最多分别为2条和11条,平均数为5.4条。若该机场跑道数不满最大需求,按照现有航班计划时间,部分时段的航班就会被延误。为了减少航班的大面积延误,必须通过航班的跑道分配和进离场时刻协调优化,使每条跑道在各个时段的进离场航班数相对均衡。

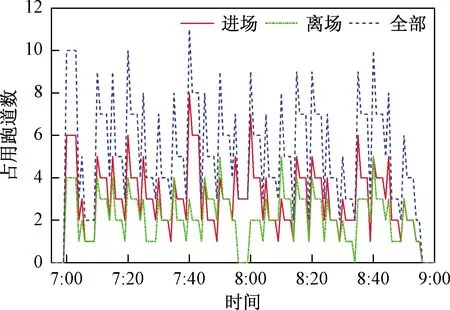
图1 全部进离场航班占用跑道的数量时变关系Fig.1 Time varying relationship between the number of occupied runways and all inbound and outbound flights

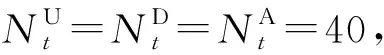
表2 不同跑道数下的模型结果对比Table 2 Comparison of model results under different runway numbers

(1)当且仅有1条跑道时,由于没有相邻跑道之间干扰,两个模型的结果一致。

(2)当2条以上跑道时,随着跑道数增加时,对于无相邻跑道干扰的FADSP,由于某个跑道可以不受干扰衔接两个相邻进离场航班,故跑道空闲时间总保持为零；同时,跑道数的增加让更少航班的进离场计划时刻调整,故航班的延误时间逐步减少。

(3)对于考虑相邻跑道干扰的FADSP,由于跑道空闲时间包含干扰时间,故其不为零；另外,当跑道数增加时,被干扰跑道的分配进离场航班数减少,这引起跑道的空闲时间也逐渐减少。同理,该模型的航班延误时间也随着跑道数量增加而减少。

(4)当相邻跑道距离较近时,为保障航空器运行间隔受扰动跑道的需要增大运行时间间隔导致部分时间无法提供航班进离场服务,需要延长时间才能使全部航班飞机起飞或降落,这导致航班的延误时间增加。因此,虽然考虑相邻跑道干扰的FADSP比传统问题的延误时间增加,但更加符合实际管制运行过程。

以5条跑道为例,全部跑道采用混合运行模式,找到6个FADSP的Pareto解,航班延误时间的上下限为1 968 min和2 208 min,跑道空闲时间的上下限为39 min和61 min。如图2所示,随着跑道的空闲时间减少,航班的延误时间增加。这是因为更多的航班进离场时刻需要调整,才能充分使用跑道资源,计算结果符合直观分析。图3给出了优化前后全部进离场航班占用跑道数的对比分析。从图3可知，在优化前,部分时刻的多个航班同时进离场导致所需要的跑道数远超过实际,因而引起航班大面积延误；进一步地,各个时段所需要的跑道数量波动变化比较大,部分时段跑道资源不够,部分时段跑道资源闲置；优化后,通过调整部分航班的进离场时刻,各个时段进离场航班数相对稳定,一方面减少航班延误,另一方面提升跑道利用效率。图4进一步给出了优化前后各个时段航班延误时间的对比,与图3的分析一致,从图4中可知，优化前,采用单跑道完成全部航班进离场,这些航班的延误发生时间是进离场航班数量大于所需占用跑道数量时,若需求大于供给时,这些航班的延误随着时间往后推移可能呈现扩大趋势，否则该趋势缩小；优化后,在多跑道运行模式下,协调全部航班的跑道分配和进离场时刻,可以极大地减少航班延误。

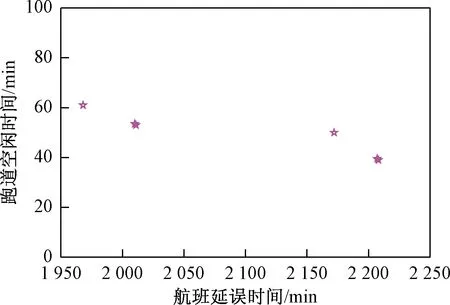
图2 Pareto解的不同目标之间变化关系Fig.2 The changing relationship among different goals of Pareto solution

图3 优化前后各个时段进离场航班占用跑道数量对比Fig.3 Comparison the number of runways occupied by flights in different periods before and after optimization

图4 优化前后各个时段航班延误时间的对比Fig.4 Comparison flight delay time in different periods before and after optimization

4 结论

考虑相邻跑道干扰的多目标FADSP,将进离场的航班分配给不同跑道,综合考虑多跑道运行模式下航空器尾流影响、管制工作负荷、航空器安全间隔和航班最大延误等约束,确定每个航班的起飞或降落时间,寻求跑道分配和进离场航班排序之间最佳资源匹配关系,同时兼顾追求航班延误最少与跑道利用效率最大两个目标。得到如下结论。

(1)随着跑道的空闲时间减少,航班的延误时间增加。这是因为更多的航班进离场时刻需要调整,才能充分使用跑道资源。

(2)当跑道数增加时,跑道的空闲时间和航班的延误时间均随之减少。这是因为无干扰跑道的分配进离场航班数量随跑道数量增加而增加,这些跑道运行彼此独立航班运行互不干扰,这引起跑道的空闲时间也逐步减少。同理,跑道数量的增加可以无需调整时刻完成航班进离场,故航班的延误时间减少。

(3)当相邻跑道距离较近时,若一个跑道正在进行航空器起飞或者着落时,受扰动跑道的此段时间禁止进离场,故该需要更多的时间才能使全部航班起飞或降落,这引起航班的延误时间增加。

然而,本文模型假设进离场航班的预计起飞或降落时间是确定的,没考虑地面保障资源、滑行路径、天气等约束导致的不确定性。因此,如何考虑相关不确定因素,研究随机航班起飞或降落时间的FADSP是一个未来值得的研究方向。