KdV孤子与BBM孤子基本特性的比较研究
韩海英,那仁满都拉
(内蒙古民族大学 数理学院,内蒙古 通辽028043)
0 引言
1895年,两位荷兰科学家Kortweg和deVries,在描述单向运动的浅水波时,在小振幅和长波长的假设下,建立了著名的KdV方程[1].KdV方程具有广泛应用,它可以作为其他许多物理系统的波模型,如无碰撞磁流体波传播问题、晶体非线性振动问题、等离子体中的声波传播问题以及非线性声波问题等多领域问题的波模型.然而,Peregrine[2]和Benjamin 等[3]分析KdV 方程的一些不足和存在问题,如建立无界区间上定义的非周期性初值问题的存在性理论时遇到的困难问题,并提出了另一种替代模型——BBM方程.他们认为从非周期性初值问题的存在性理论的本质上看,BBM 方程比KdV 方程更适合长波模型[2].关于KdV方程和BBM方程的研究文献很多,文献[4]中研究正则长波方程(BBM方程)孤立波的相互作用,指出孤立波相互作用后出现小的频散尾巴.文献[5]研究BBM方程孤立波的碰撞问题,指出BBM方程的孤立波碰撞后不出现小尾巴,碰撞具有孤立子特性.文献[6]利用基于Galerkin方法的三次B样条有限元法,研究等宽方程的不同孤立波的相互作用并指出孤立波的相互作用可产生幅度很小的子波.文献[7]利用Petrov-Galerkin方法,研究等宽方程的两个和三个孤立波的相互作用并给出与文献[6]类似的结果.文献[8]采用数值方法对修正的等宽方程的孤立波解的相互作用性质进行了研究.文献[9]中给出了BBM方程的拟线性隐式差分格式和非线性隐式差分格式.关于KdV方程的研究更多更全面,可参阅文献[10].文献[11-13]对KdV类方程和BBM类方程进行了数值研究.
本文将利用伪谱方法,对KdV方程和BBM方程描述的两种孤子的形状结构、相互作用特性以及动力学稳定性等基本特性进行详细的数值研究和比较分析.
1 两种孤子方程及其算法
本文研究标准形式的KdV方程和BBM方程

这里α和β是与介质有关的常数,当α=1,β=δ时方程(2)也称为等宽方程[6-7].方程(1)和(2)是非线性物理中的两种重要方程,多位作者采用不同的方法进行过研究[4-14].本文采用更简便、直接且精度较高的伪谱方法研究这两种方程.
首先构造两种方程的伪谱算法格式.根据伪谱方法的基本思想[15-17],对方程(1)作傅里叶变换

上式中,符号“∧”表示对应函数的傅里叶变换,i是虚数单位,k是变换常数.方程(3)两边乘以e-ik3βt,并令v∧=e-ik3βtu∧可得

因为

把(5)式代入(4)式得

上式中,F表示傅里叶变换,F-1表示傅里叶逆变换.由方程(6)可看出,通过作快速傅里叶变换和乘积分因子的技巧,已消掉了方程(1)中导致数值频散的高阶空间导数项并得到了关于v∧的常微分方程.方程(6)可以用龙格库塔方法直接求解,然后再由(5)式可求得原方程的解u,这种方法也称为积分因子方法[16-17].
由于方程(2)中包含混合导数项uxxt,所以方程(2)的处理不同于方程(1),首先令

对上式作快速傅里叶变换可得

也可写为

根据傅里叶变换的性质,可把上式推广得到

利用(9)和(10)式,把方程(2)改写为

此方程是关于v的常微分方程,所以可利用龙格库塔方法直接求解出v,然后用(9)式可求解得到u.
2 两种孤子的基本特性
KdV方程和BBM方程的孤子解分别为

这里Ak和Ab是两个任意常数,分别表示KdV孤子和BBM孤子的振幅.从孤子解(12)和(13)可看出,KdV孤子的传播速度和宽度都与其振幅有关,而BBM孤子的传播速度与其振幅有关,但宽度与其振幅无关.因此,当Ak≠Ab时两种孤子的幅度、宽度和传播速度都可以不相同,而当Ak=Ab=A时两种孤子的幅度和传播速度相同,但宽度不相同.容易计算得到,时两种孤子的宽度相同时KdV孤子的宽度小于BBM孤子的宽度,时KdV孤子的宽度大于BBM孤子的宽度.从图1(参数选为α=6.2,β=0.01,A=1)中绘制的两种孤子的传播图上也可看到上述特性.
孤立子的一个重要特性就是相互作用之后还能保持它们原有的波形结构、振幅和传播速度而继续传播,即孤立子的碰撞具有粒子弹性碰撞的特性.为了检验KdV孤子和BBM 孤子是否都具有这种特性,我们数值模拟了双KdV孤子和双BBM孤子的相互作用过程.计算时以(12)和(13)式作为初始条件,采用区间[-π,π]上的周期边界条件,参数选取为α=6.2,β=0.01,双孤立子的幅度选为A1=1,A2=0.4,模拟的结果在图2至图5中给出.图2所示的是幅度、宽度和传播速度都不同的双KdV孤子的相互作用,可看出双孤子相互作用之后都能够保持原有的波形结构、振幅和传播速度而继续传播,只是它们的相位产生了明显的变化(如图4所示),相比于大幅孤子显然小幅孤子的相位变化更明显.KdV孤子的这些特性是人们熟悉的结果.图3所示的是幅度和传播速度不同、宽度相同的双BBM孤子的相互作用.从图3可看出,在计算条件和计算精度范围内,BBM孤子相互作用之后还能基本保持原有的波形结构、振幅和传播速度而继续传播,相位产生了明显变化(如图5所示).但如果放大图3就可看到(图已忽略),BBM孤子相互作用之后出现幅度很小的尾波.因此,严格讲BBM孤子的相互作用具有近似的粒子弹性碰撞性质.

图1 KdV孤子(红线)和BBM孤子(蓝虚线)的传播Fig. 1 Propagation of KdV solitons(red line)and BBM solitons(blue dotted line)

图2 双KdV孤子的相互作用Fig. 2 Double KdV solitons interaction

图3 双BBM孤子的相互作用Fig. 3 Double BBM solitons interaction

图4 双KdV孤子相互作用的等值线图Fig. 4 Isoline map of the interaction of double KdV solitons

图5 双BBM孤子相互作用的等值线图Fig. 5 Isoline map of double BBM solitons interaction
3 两种孤子的动力学稳定性
为考察两种孤子受到小扰动之后还能否保持原有的波形结构、幅度和传播速度,本节研究了两种孤子传播时受到高斯小扰动的情况.假设两种孤子受到了同样的高斯扰动,其表达式为:
式中A0为高斯扰动幅度,μ为高斯扰动宽度因数.数值计算时,仍采用区间[-π,π]上周期性边界条件,初始条件分别为uk(x,0)+u′(x,0)和ub(x,0)+u′(x,0).为使两种孤子的初始幅度和宽度完全相同,参数选取为A=1,α=3,β=0.01,小扰动幅度取为A0=0.02,宽度取为μ=40.一般来讲,考察的波在经过较长时间的演化后,如果扰动的幅度没有产生明显的增加,受扰波的波形结构、幅度和传播速度基本保持不变,则可判定该波是动力学稳定;如果扰动的幅度产生明显的增加,受扰波的波形结构、幅度和速度发生明显改变,则可判定该波是动力学不稳定.图6给出的是t=3.5 时刻的受扰KdV孤子波形,可看得出,随着时间的推移,初始时刻的局部高斯扰动,逐步弥散整个计算区域并成为小扰动波,但其幅度没有增加,而受到扰动影响的KdV孤子的波形、幅度和传播速度都没有产生明显变化,相位产生了少量变化并出现了扰动产生的尾波.从图7显示的受扰孤子与未受扰孤子在同一时刻的差异(Δuk表示)图上也能看到这些特点.当高斯扰动的幅度增大到A0=0.05 时,KdV孤子仍能够很好地保持其原有的波形、幅度和传播速度(图忽略).这表明KdV 孤子具有很好的抗干扰性和动力学稳定性.在图8 中给出的是t=3.5 时刻的受扰BBM孤子波形.可清楚地看到,BBM孤子从初始位置开始传播并压过高斯波包,传播到如图所示位置.此时的BBM孤子的波形、幅度和传播速度都没有产生明显变化,也没有产生尾波,只是相位产生了少量变化.有趣的是在此过程中高斯波包并没有弥散到整个计算区域,而是还能基本保持原有形状结构和局部特点(如图9所示).当高斯扰动的幅度增大时,BBM孤子仍能够很好地保持其原有的波形、幅度和传播速度,此过程中高斯波包也没有弥散开,还能基本保持其局部特点(图忽略).由此可见,在笔者的计算精度范围内,BBM孤子具有更强的保持波形结构的抗干扰特性,因为它受扰后并没有明显产生尾波,也没有把扰动波包弥散到整个区域.

图7 受扰与未受扰KdV孤子的差异Fig. 7 The difference between disturbed and undisturbed KdV solitons
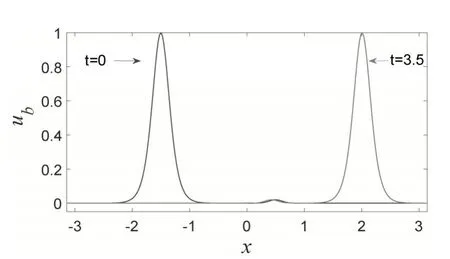
图8 受扰动的BBM孤子Fig. 8 The perturbed BBM solitons

图9 受扰与未受扰BBM孤子的差异Fig. 9 The difference between disturbed and undisturbed BBM solitons
4 结论
KdV方程和BBM 方程是在非线性波动问题中具有重要地位的两种方程,对两种方程所描述孤子特性的研究具有重要意义.本文首先构造了KdV方程和BBM方程的伪谱算法并利用该算法,对KdV孤子和BBM 孤子的形状结构、相互作用特性以及动力学稳定性等基本特性进行了详细的数值研究.研究表明,KdV孤子的传播速度和宽度都与其幅度有关,而BBM孤子的传播速度与其幅度有关,但宽度与其幅度无关.因此,KdV孤子的相互作用是幅度、宽度和传播速度都不同的双孤子相互作用,而BBM孤子的相互作用是幅度和传播速度不同、宽度相同的双孤子相互作用.KdV孤子的相互作用具有粒子弹性碰撞性质,而BBM 孤子的相互作用具有近似的粒子弹性碰撞性质.KdV 孤子和BBM 孤子都具有很强的抗干扰性和动力学稳定性,相比而言BBM孤子具有更强的保持波形结构的抗干扰特性,因为它受扰后并没有明显产生频散尾波,扰动波包也能够基本保持原有形状结构.

