高精度再生指纹的可见光室内定位算法

张 旭，姚善化

(安徽理工大学 电气与信息工程学院，安徽 淮南 232001)

近年来随着可见光通信技术的不断发展，可见光在室内定位方面具有精度高、成本低、安全性高等优势，越来越多的研究人员将可见光用于室内定位[1-2]。

基于指纹库的室内定位方法，因其定位精度高、部署简单而被广泛地采用[3-5]。指纹定位主要分两个阶段，离线阶段和在线阶段，离线阶段采集信号强度构建指纹库，在线阶段根据定位目标接收信号强度，利用K近邻算法(K Nearest Neighbor，KNN)估算出定位目标的位置。离线阶段指纹库采集得越详细，则定位精度越高，然而过大的指纹库不仅导致采集的工作量增加，还会使得在线匹配阶段的时间增加[6]。目前针对降低指纹库采集工作量的研究有：利用插值算法根据已知点的信号强度来估算未知点的信号强度，定位精度有待提高[7-8]；利用低秩矩阵填充理论来恢复只有少数采集点的指纹库，算法的复杂度较高[9-10]；利用移动众包的方法，通过用户数据就能进行定位，非专业的勘测数据可信度受到质疑，还会产生大量冗余的数据[11-12]。通过分析研究，本文通过测量参考位置的光信号强度，利用光信号的传播模型来估算出其他位置的光信号强度，以此来构建再生指纹库；同时提出改进的加权K近邻算法(Weighted K Nearest Neighbor,WKNN)[13-14]，用平方弦距离度量替代欧氏距离度量，同时结合发光二极管(Light-Emitting Diode,LED)的稳定性，选取平方弦距离最近的k个点来估计定位目标的位置，在保证定位精度的同时大大降低了采集数据的工作量。本文所提算法相较于指纹识别融合贝叶斯算法以及指纹数据滤波与聚类算法，采集的数据信息更少，算法复杂度更低，构建指纹的时间更短。

1 基于光传播模型构造指纹库

1.1 光传播模型

一般情况下，可见光室内定位采用LED作为光源，光电二极管(Photodiode,PD)作为接收器，光源的发光强度服从朗伯辐射模型，在只考虑视距(Line of Sight,LOS)的情况下，如图1所示，PD接收到的功率可以表示为：

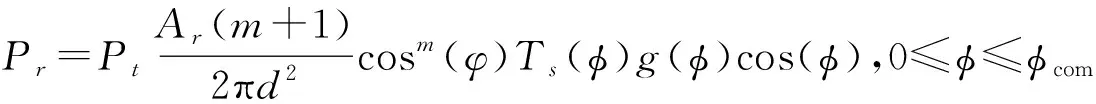
(1)

(2)

式中Pt是LED的发射功率，Ar为PD的有效接收面积，m为朗伯发射级数，φ1/2是LED发光的半功率半角，d为LED与PD之间的直线距离，φ是发射角，φ是入射角，φcom是接收视场角，入射角小于等于接收视场角，Ts(φ)是接收器的带通光滤波器透射率，g(φ)是非成像聚光器的增益。

图1 可见光定位模型

1.2 离线构建指纹库

假设接收机的位置与发射器的位置平行，则入射角φ和发射角φ是相等的，若在实际测量时接收机与发射器的位置不平行，使用光传播模型构建的指纹库与真实指纹库之间的误差会很大，导致在定位阶段通过WKNN算法估算出的定位坐标误差会很大，必须要保证入射角与发射角相等。在忽略Ts(φ)和g(φ)的时候，位于i点的接收功率Pr,i为：

(3)

取朗伯发射级数m为1，其中cos(φi)=h/di，h为接收机到LED的垂直距离，则位于j点的接收功率可以用i点的接收功率来表示：

(4)

将定位区域均匀划分成大小相等的小网格，在每个网格中选取参考点来测量接收信号强度，只选取l个参考点来测量信号强度，将这l个参考点根据公式(4)依次来构建虚拟指纹库，这样就构建了l个指纹库，将这l个指纹库合并在一起，则指纹库中每个位置的信号强度就有l个，将每个位置的l个信号强度相加求其均值作为该位置最终的信号强度，这样就可以构建出再生指纹库。

2 改进的WKNN算法

离线阶段通过光传播模型构建的指纹库与真实指纹库之间存在着误差，为了进一步提高定位精度，在线定位阶段采用改进的WKNN定位算法。通过测量定位目标点接收到LED的信号强度，计算目标点的信号强度与指纹库中每一点的信号强度之间的距离，选取距离最近的k个点的信号强度来估计目标位置，现有的WKNN算法大多采用信号之间的欧氏距离作为度量，而欧氏距离表示的只是定位目标和采集点信号之间的绝对位置，并不能很好地反映采集点之间的相对位置，定位会存在偏差，故而采用平方弦距离代替欧氏距离，可以很好地改善定位误差，即：

(5)

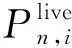
(6)

(7)

(8)

式中Wi,k为定位目标点i与距离最近的k个点之间的权重，则通过改进的WKNN算法估算出定位目标点的位置为：

(9)

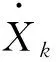
3 实验仿真与结果

3.1 仿真参数的设置

通过MATLAB仿真软件，在只考虑视距的情况下，采用4个LED来进行可见光室内定位，具体方法为：将定位区域均匀划分成大小相同的小网格，离线阶段构建真实指纹库，选取其中的25个参考点通过光传播模型构建虚拟指纹库，如图2所示，选取剩余位置点作为在线阶段的测试点，共计576个位置点，对比所提算法下再生指纹库和真实指纹库之间的定位精度，验证所提算法的可行性，实验参数如表1所示：

表1 仿真环境参数

图2 参考点与测量点的位置

3.2 实验结果分析

定位阶段采用改进的WKNN算法，k的取值对定位算法具有一定的影响。当k值太小时定位目标邻近的区域就会很小，定位模型变得很复杂，定位目标的估计位置更贴近于再生指纹库，近似误差较小；然而k的取值较小会导致随机误差增大，不能很好地反映定位目标的估计位置，而且估算到的定位目标的位置与真实位置也会存在较大的差距，估计误差较大。当k值太大时则正好相反，需要选择最合适的k值使得定位算法的精度最高。因此我们研究了改进的WKNN算法在不同k值下的定位精度，如图3所示。

图3 改进WKNN不同k值下的平均定位误差

在k取5的时候效果最好，定位的平均误差最小。同时LED的稳定性对定位系统的精度也会产生一定的影响，由于LED受到多径效应的影响，稳定性以及定位精度都会降低，增加LED的个数可以提供更均匀的光强分布，使得定位精度更高，但是计算量也会增加。在不增加LED个数的前提下，通过统计定位区域内参考点来自各个LED的信号强度并计算每个LED的信号强度方差，方差越小表示各个参考点上测量的LED的信号强度偏离平均值越小，该LED的稳定性就越好。在WKNN算法中加入LED信号强度的方差，可以减少由于LED不稳定所带来的定位误差。

通过仿真对比了改进的WKNN算法和WKNN算法，如图4所示，改进的WKNN的定位精度相对于WKNN的定位精度有所提高，定位误差更小。

为了验证所提算法的有效性，与二维插值法构建的指纹库和真实指纹库的定位精度进行对比，如图5所示。

图4 WKNN和改进的WKNN的平均定位误差

图5 不同指纹库下的平均定位误差

在平均定位误差为5 cm时，光传播模型再生指纹库的定位精度累积概率分布为90%，远高于二维插值法构造指纹的8%，略低于真实指纹库的97%，表明所提方法的定位精度要高于二维插值法的定位精度，相比于真实指纹的定位精度要略低，但是本次实验只采集了25个位置点的光信号强度，而真实指纹库中需要采集625个位置点的光信号强度，本文所提方法大大降低了指纹库构建的工作量，而且定位精度差别不大。

4 结论

研究结果表明所提出的算法在前期指纹库的采集方面可以大大降低工作量，同时定位精度与真实指纹库相近，相比于二维插值方法构建的指纹库，定位精度更高。接下来的研究会进一步在实际应用中验证算法的可行性，同时考虑多径反射的情况，进一步提高定位精度。