基于BP神经网络的增高腿注塑工艺参数优化

廖生温，王玉勤，刘 磊,刘 婧

(1.巢湖学院 机械工程学院，安徽 巢湖 238000；2.芜湖金鹏汽车部件有限公司，安徽 芜湖 241000)

塑料制品具有可塑性强、制造成本低、电绝缘性优良等优点，在国民经济中应用广泛，人们对其质量的要求也越来越高[1]。注塑成型占塑料件生产的三分之一左右，是塑料成型的主要加工方法之一，在制造业中扮演着重要角色。塑料件质量的优劣直接影响其生产效率和装配使用，而决定塑料制品质量和生产效率的因素除了注塑模具质量设计的好坏外，还有一个关键因素在于成型工艺参数设置[2]。与传统注塑模具设计方法相比，注塑CAE技术能对塑件的缺陷进行提前预测与控制，减少模具反复试模、修模次数，缩短模具的开发周期，提高效率，降低企业经营生产成本[3]。目前，对优化注塑成型工艺参数方面已有许多学者进行了大量研究。如：林幼文[4]等采用Moldflow软件对汽车进气格栅的浇注系统进行CAE仿真分析并改进，同时运用GRNN神经网络对汽车进气格栅的注塑工艺参数进行优化，解决了熔接痕和翘曲变形的质量问题，满足了实际生产需要。杨振[5]等采用Moldflow软件对汽车后视镜外壳的模流过程进行模拟仿真分析，设计汽车后视镜外壳翘曲变形量的BP神经网络，取8组数据进行训练，另外8组样本数据进行BP网络预测，对比Moldflow软件模拟值与预测值，得到误差在允许范围内，表明所设计的BP网络模型正确，但未进行实验验证。孙丽丽[6]等选取5个注塑工艺(熔体温度、模具温度、注射压力、保压时间、保压压力)，以充填时间、体积收缩率、总翘曲变形量作为实验目标，确定网络层数、节点及传递函数，建立多输入-多输出的BP神经网络模型，并进行训练与预测，验证了BP神经网络9组预测数据与Moldflow模拟数据的误差较小，进行制件试生产，得到储物盒制件表面无明显翘曲变形和熔接痕，满足质量要求。研究成果显示，各种代理模型能够准确地控制和预测塑料件的翘曲变形、体积收缩率和缩痕指数，有效提高优化效率[7]。

参考上述文献，对增高腿的注塑成型过程在Moldflow软件中进行模拟分析，通过极差分析法确定其注塑成型工艺参数对体积收缩率和缩痕指数的影响重要程度。然后建立BP神经网络模型对增高腿的体积收缩率和缩痕指数进行预测，得到训练后的预测值与Moldflow模拟值基本一致，提高了设计效率，可为实际应用提供参考。

1 注塑件结构及工艺分析

该塑件为圆柱状的增高腿，是用于儿童玩具桌的增高，壁厚均匀，如图1所示。塑件最大尺寸为长130 mm、宽44.5 mm、高44.5 mm。由于增高腿在儿童玩具桌反复拆解时拼插牢固，因此要求产品零件内外表面光滑，不得有划痕、飞边、毛刺、翘曲变形等不良缺陷，表面粗糙度要求为Ra0.8 μm。聚丙烯材料属于高分子材料，具有无味、无毒、密度小、良好的耐化学性、电绝缘性、耐热性、高强度机械性能等优点，在玩具塑料产品生产中应用广泛。该增高腿采用A Schulman GMBH化学公司的聚丙烯材料(牌号：POLYFLAM RIPP 3625 CS1)，其PVT曲线如图2所示。

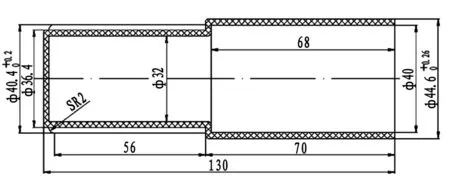
图1 增高腿

图2 PP的PVT曲线

2 正交实验设计与分析

正交实验设计是用于组合多因素多水平实验而获得最优水平组合的实验设计方法，由于影响注塑件的收缩率因素有很多，因此在工程实践中应用广泛[8]。

本研究选取6个工艺参数(熔体温度、模具温度、注射压力、注射时间、保压压力、保压时间)作为实验因素，并根据所选材料、工艺条件、成型设备以及实际生产状况等多种因素来确定各个注塑工艺参数的水平值，在模流实验模拟过程中忽略各工艺参数间交互作用所产生的影响。最终确定该试验为五水平六因素试验，采用L25(56)的正交表，如表1所示。根据正交表设计进行25次实验，得到注塑成型工艺参数对增高腿缩痕指数和体积收缩率考核指标的结果，如表2所示。

2.1 注塑工艺参数对增高腿的缩痕指数的影响

对注塑件产生缩痕的可能性通常用缩痕指数来表示，其值越大，表明制件产生缩痕或缩孔的可能性就越大[9]。通过计算增高腿注塑成型正交实验结果得到其缩痕指数的极差分析表如表3所示。得到各工艺参数影响增高腿缩痕指数的重要程度顺序为：熔体温度>模具温度>注射时间>保压压力>保压时间>注射压力。

表1 正交试验的六因素五水平值

表2 增高腿注塑成型正交实验方案及结果

表3 各工艺参数对缩痕指数的极差分析表

表3中k1、k2、k3、k4、k5及K1、K2、K3、K4、K5分别表示增高腿注塑成型正交实验各因素在五个水平值下缩痕指数的均值与总和，极差R表示缩痕指数均值的最大值与最小值之差。

为直观反映增高腿注塑工艺各参数对缩痕指数的影响重要程度，绘制各注塑工艺参数因素对缩痕指数的影响趋势图如图3所示。

图3 正交试验各因素对增高腿缩痕指数的影响趋势图

对增高腿注塑工艺各参数对缩痕指数进行极差分析可以得到：取缩痕指数的因素、水平的最小值就是最佳工艺参数组合，即A1B2C3D1E5F5，即当增高腿注塑工艺参数的模具温度为50 ℃、熔体温度为205 ℃、注射压力为98 MPa、注射时间为0.8 s、保压压力为43 MPa、保压时间为30 s时缩痕指数数值最小。在正交实验表中没有该组工艺参数组合，运用Moldflow模拟得到缩痕指数为1.362%，如图4，其结果得到优化。

图4 增高腿A1B2C3D1E5F5工艺参数的缩痕指数

2.2 注塑工艺参数对增高腿的体积收缩率的影响

塑料的收缩率是塑料本身热胀冷缩而导致其制品尺寸缩小的现象，是指塑料制品从模具中取出冷却至室温时尺寸缩小的程度[10]。它是影响制件质量的重要因素之一，因此在注塑成型过程中需尽可能减小制件的体积收缩率值。其计算公式为：

(1)

式中，Sv为注塑成型制品的收缩率；Vm为常温下注塑模腔的体积；Vc为常温下注塑成型制品的体积。

通过计算增高腿注塑成型正交实验结果得到其体积收缩率的极差分析表如表4所示。

表4 各工艺参数对体积收缩率的极差分析表

表4中k1、k2、k3、k4、k5及K1、K2、K3、K4、K5分别表示增高腿注塑成型正交实验各因素在五个水平值下体积收缩率的均值与总和，极差R表示体积收缩率均值的最大值与最小值之差。

由表4可知，各工艺参数影响增高腿体积收缩率的重要程度顺序为：溶体温度>保压时间>注射压力>模具温度>注射时间>保压压力。为直观反映增高腿注塑工艺各参数对体积收缩率的影响重要程度，绘制各注塑工艺参数因素对体积收缩率的影响趋势图如图5所示。

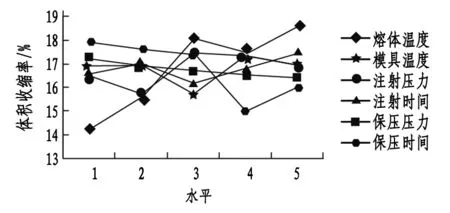
图5 正交试验各因素对增高腿体积收缩率的影响趋势图

对增高腿注塑工艺各参数对体积收缩率进行极差分析可以得到：体积收缩率的因素、水平的最小值就是最佳工艺参数组合，即A1B3C2D3E5F4，即当熔体温度达到205 ℃，模具温度达到60 ℃，注射压力为97.5 MPa，注射时间为1.7 s，保压压力为38 MPa，保压时间为25 s时体积收缩率为12.82%，如图6，其结果得到优化。

图6 增高腿A1B3C2D3E5F4工艺参数的体积收缩率

3 BP神经网络优化

3.1 BP神经网络模型建立

采用单隐含层的前馈网络结构建立BP神经网络模型，输入层是以熔体温度、模具温度、注射压力、注射时间、保压压力和保压时间等六个注塑工艺参数作为神经网络输入参数，以增高腿的体积收缩率为输出目标函数[11]。在BP神经网络结构中，设置输入层的节点数为6，输出层的节点数为2，隐含层的层数为m，其神经网络拓扑算法模型如图7所示。

图7 BP神经网络结构图

隐含层的节点数s通过经验公式(2)计算得到：

(2)

上式中：m为隐含层节点数；

n为输入层节点数；

l为输出层节点数；

a为1-10之间的常数。

根据公式(2)计算初步选定m=10，该值可在BP神经网络训练时的实际情况进行适当的调整。

3.2 BP神经网络模型训练与验证

在构建BP神经网络模型时，为使模型更好满足数据样本的精度和快速收敛性要求，对数据样本作归一化处理，公式为(3)。并设置S型正切函数tansig为隐含层函数，输入层函数为非线性传递函数logsig，输出层函数为线性传递函数trainlm。设置最大训练次数为5000次，学习速率为0.01，性能目标误差为0.0001。当BP神经网络模型的训练目标误差小于0.0001或者训练次数达到5000时，训练自动终止。对BP神经网络模型的输出值作反归一化处理以得到实际模拟值。

(3)

式中，xi、xmax、xmin分别为神经网络训练的输入或输出数据、最大值、最小值。

对增高腿的模拟值(见表2)随机抽取16组数据为检验样本来训练BP神经网络模型，得到的预测结果如下表5所示，在正交模拟数据中随机抽取16组数据作为检验样本，其余9组作为测试样本，并计算两者之间的相对误差，将Moldflow模拟值与BP神经网络预测值进行对比。

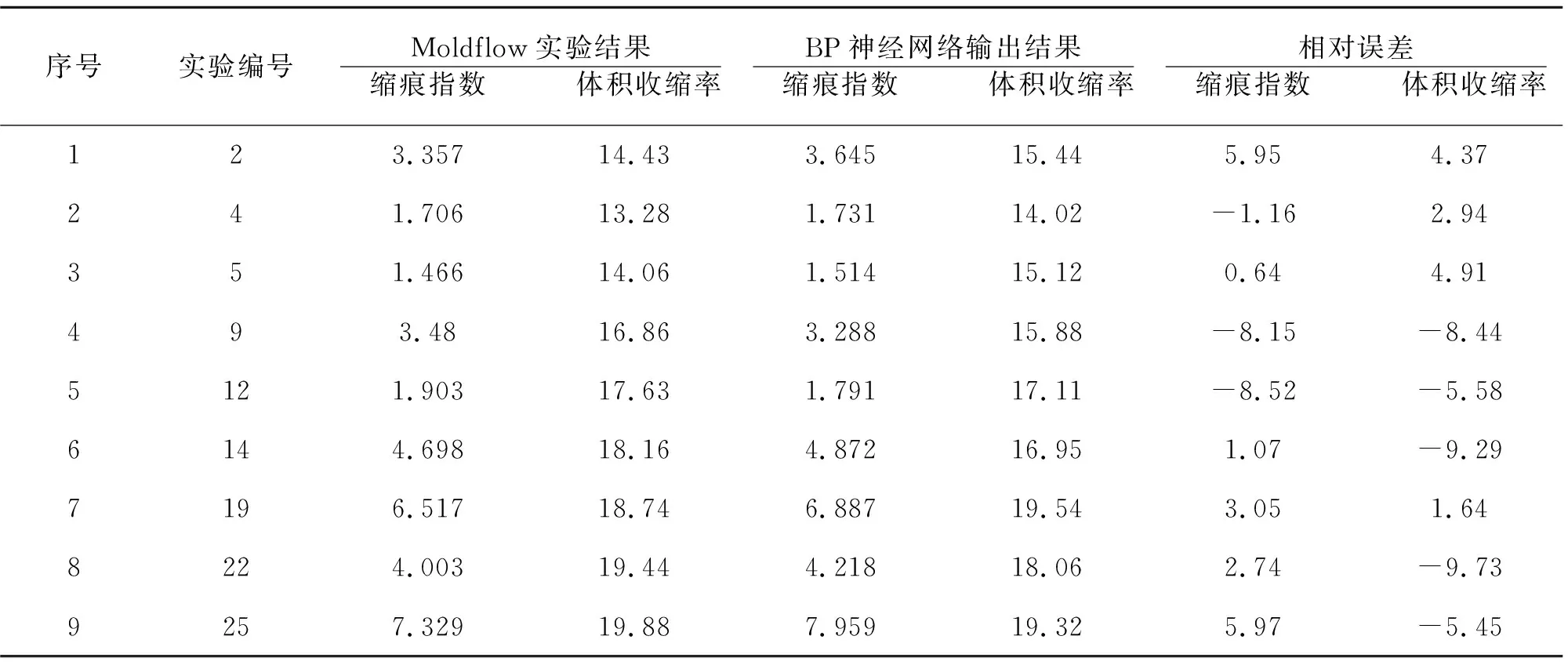
表5 Moldflow实验结果与BP神经网络输出结果比较 %

为了对比BP神经网络输出值与Moldflow模拟值之间的吻合度，根据表5做出图8所示的神经网络输出值与 Moldflow 模拟值对比曲线图。

图8 BP 神经网络输出值与 Moldflow 模拟值对比曲线图

从表5和图8中的结果可以分析得到：增高腿的缩痕指数和体积收缩率的相对误差都小于10%。这说明正交实验的模流结果与神经网络的预测结果比较接近，吻合程度较高，也说明所设计的BP神经网络模型较好，预测精度较高。

综上所述，运用正交实验分析、BP神经网络，模流CAE仿真分析能获得较佳的注塑成型工艺参数，使增高腿的注塑质量得到明显改善，增高腿实际注塑生产实物如图9所示。

图9 增高腿试模制件

4 结论

本研究基于Moldflow软件和BP神经网络，结合正交实验法，以熔体温度、模具温度、注射压力、注射时间等6个注塑工艺参数为影响因子，寻找使增高腿的缩痕指数和体积收缩率变量最小的工艺参数组合[11]，得到的结论如下：

基于正交实验法，设计了L25(56)正交实验方案并进行模流仿真分析，通过极差分析得到各工艺参数影响增高腿体积收缩率的重要程度顺序为：溶体温度>保压时间>注射压力>模具温度>注射时间>保压压力。其最佳工艺参数为：熔体温度达到205 ℃，模具温度达到60 ℃，注射压力为97.5 MPa，注射时间为1.7 s，保压压力为38 MPa，保压时间为25 s，其体积收缩率为12.82%。

以增高腿的注塑工艺参数作为神经网络输入参数，体积收缩率为输出参数，建立三层BP神经网络预测模型。通过随机抽取16组Moldflow仿真结果作为BP神经网络初始训练样本并进行验证，发现 BP 神经网络的预测值和Moldflow的模拟值之间的误差较小，说明构建的BP神经网络模型具有较好的预测精度。对增高腿进行试生产，成型后的增高腿制件表面质量良好，无明显缺陷。