风火打捆系统中单机聚合对详细模型SSO的影响

苏勋文， 崔含晴， 裴禹铭， 安鹏宇

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

随着风电等可再生能源的开发利用，风火打捆外送迅速发展，在提高输电能力的同时也给系统的稳定性带来挑战。2015年7月，哈郑直流送端换流站附近某火电厂出现因次同步振荡导致的切机事故，与送端交流系统接入大量风电有关[1-2]。

在对风火打捆系统的研究中，由于风机的容量一般很小，风电厂一般由上百台风机组成，对每台风机都进行详细的建模仿真会极大增加工作量与仿真时间，且同一风电场中风机的风速差异不会过大[3-5]。因此，在现有的研究中一般视风电场中风机风速相同，采用单机容量加权聚合法等效聚合为一台风机进行研究。

刘华坤等[6-7]基于阻抗模型分别讨论了采用聚合RLC电路模型双馈风电场中风速、控制参数对SSO的影响，分析了详细模型的多个具有串补系统风电场的次同步谐振稳定性。杨琳[8]采用复转矩系数分析法分析了风电场接入位置对火电机组次同步阻尼特性的影响。高本锋等[9]将风电机组等效聚合，讨论了风速、转子侧换流器PI参数、串补度、线路电阻对均会对系统稳定性的影响。张学伟[10]为验证等值方法的准确性，分别对比了详细模型与等值模型在稳态运行及故障时的有功及无功输出特性。但未分析复转矩法下的风电机组聚合以及忽略风电场风速差异是否会对系统次同步振荡产生影响。

笔者利用PSCAD/EMTDC电磁仿真平台，在IEEE第一标准模型的基础上，搭建了风火打捆系统的详细模型和聚合模型，采用复转矩系数分析法，分析相同运行状态风机与风速不同风机聚合后对系统SSO的影响，通过时域仿真进行验证。

1 风机聚合对系统电气阻尼系数影响

图1为系统简化原理，E、δ分别为火电机组机端电压和相角，U1、θ分别为DFIG并网母线端电压和相角，U2为无穷大母线端电压，记无穷大母线端电压相角为0。Pe、Qe分别为火电机组输出的有功功率和无功功率，Pg、Qg分别为DFIG输出的总的有功功率和无功功率，Pm、Qm分别为由DFIG并网端母线流向无穷大母线的有功功率和无功功率。基于复转矩系数法的原理，忽略有功功率对母线电压幅值的影响和DFIG侧阻抗的影响简化原理，根据有功功率平衡，分析风机聚合对火电机组次同步振荡的影响[11]。

图1 风火打捆系统简化原理

由系统功角特性，火电机组输出的有功功率及DFIG并网端流向无穷大母线的有功功率可表示为：

(1)

(2)

式中，Z1、Z2——线路阻抗。

在火电机组转子侧加入频率为ω0，幅值为A的小幅值扰动Δω，将(1)(2)线性化：

Δω=Asinω0t，

(3)

(4)

式中，γ——火电机组机端与母线间初始相角，γ=δ0-θ0。

根据有功功率平衡为

ΔPm=ΔPe+ΔPg。

(5)

将式(3)、(4)代入式(5)，整理得：

Δθ=k1Δδ+k2ΔPg，

(6)

将式(6)代入式(3)，可得

此时，火电机组电气转矩增量ΔTe为：

(7)

根据复转矩系数法的原理，若聚合前后η值未变，则聚合对火电机组SSO无影响，由式(7)可知多台风机参数相同时，聚合前后对风火打捆系统SSO的影响一致。考虑实际风电场内因海拔高度、尾流效应等因素导致风机风速不同时的情况，当n台风机的风速不同时，聚合模型中DFIG风速采用等效风以保持聚合前后输出同样的有功功率，即聚合模型和详细模型中系统SSO阻尼特性相同。

2 系统建模

风火打捆系统结构如图2所示。双馈风电机组(DFIG)和火电机组分别经升压变压器T1、T2，升压后经串补线路连接至无穷大系统[12-13]。

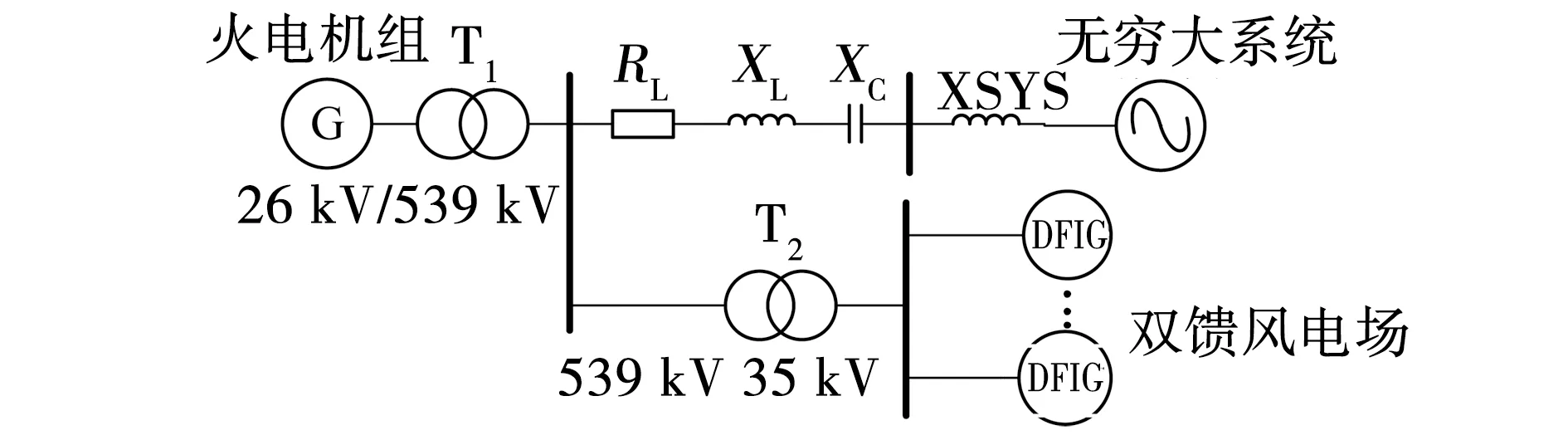
图2 风火打捆系统结构

2.1 火电机组模型

火电机组模型为IEEE第一标准模型，机组额定容量为892.4 MVA，额定频率为60 Hz。由于次同步振荡和发电机的轴系息息相关，次同步振荡主要考虑的是轴系损伤的可能性，因此，该问题进行研究需要考虑轴系弹性系数的影响，建立相应的轴系数学模型。

根据图3的轴系结构可知，轴系运动方程[14]：

式中：δi——第i个质量块的电气角位移；

ωi——第i个质量块的电气角速度。

图3 轴系结构示意

K12(δ2-δ1)-K23(δ2-δ3),

K23(δ3-δ2)-K34(δ3-δ4),

K34(δ4-δ3)-K45(δ4-δ5),

K45(δ5-δ4)-K56(δ5-δ6),

式中：TJi——第i个质量块的惯性时间常数；

Tmi——第i个质量块上的原动转矩；

Dii——第i个质量块的自阻尼；

Di,i+1——第i和第i+1个质量块间的互阻尼。

在具有串补的系统中，当电气谐振频率与发电机轴系的模态频率互补时，便有发生次同步振荡的风险，该系统的模态频率如表1所示。

表1 火电机组轴系模态频率

2.2 双馈风机模型

双馈风电场主要包含双馈风机和风机换流器两部分，其结构如图4所示。为了保证双馈风机与系统能量的双向流动，双馈风机定子绕组直接与电网侧相连，而转子绕组经换流器与电网相连[15]。换流器控制系统根据双馈风机的运行状态来调整风电场内的能量流动。

图4 双馈风机结构示意

为了提高风机参数的代表性，提高仿真结果的可信度，分别将文献[16-17]的风机参数作为算例1、2进行实验。单台风机的参数如表2所示。

表2 单台风机参数

风能在风机叶轮上产生的转矩及风机获取的机械功率为

Tw=Pw/ωw，

式中：Tw——叶轮产生的转矩；

Pw——从风机获得的机械功率；

ωw——风机转速；

ρ——空气密度;

S——风机叶片扫过的面积;

vw——进入风机后的风速;

Cp——性能系数。

3 双馈风机聚合模型

采用单机加权等值聚合法对风机进行等值聚合，等值公式[18-19]为：

SGeq=nSG,

式中：n——风机台数；

SG——单台风机容量；

XG——风机中的电抗参数；

RG——风机中的电阻参数。

对变压器采用同样的方法等值聚合，等值参数为：

STeq=nST,

式中：ST——单台变压器容量；

XT——变压器的电抗参数；

RT——变压器的电阻参数。

双馈风机换流器等值参数为：

SEeq=nSE

式中：SE——单台换流器的额定容量；

ZE——单台换流器阻抗。

聚合模型中风机的风速为等效风速，即根据图5所示风速-功率曲线得到每台风机的功率，求取功率平均值后，根据风速-功率曲线反推等效风速[20]。

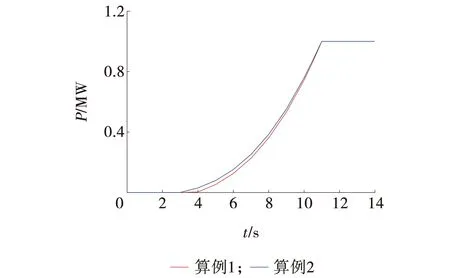
图5 单台风机的风速-功率

4 DFIG聚合的复转矩

为了探究DFIG等值聚合对风火打捆系统SSO的影响，分别考虑风机运行状态完全相同以及风机风速存在差异两种工况进行实验。

工况一为四台同型号、同参数的DFIG以相同风速11 m/s并网。采用单机加权等值聚合法对DFIG等值。算例1、2等效风速均为11 m/s。

工况二在情况一的基础上改变风机风速，四台DFIG分别以11、11、9、7 m/s运行，并采用同样的方法将上述风机聚合，根据上述等效风求取原则得聚合后算例1等效风速为9.72 m/s，算例2的等效风速为9.76 m/s。

为了量化等值产生的误差，以风火打捆系统详细模型仿真结果作为基准，误差评价指标为

(8)

式中：t1——计算起始时间；

t2——计算结束时间；

Z1——详细模型电气量；

Zeq——聚合模型电气量。

为验证聚合的准确性，分别测得情况一、二聚合前后DFIG输出有功功率如图6、7所示。由图6、7可以看出，DFIG稳定运行后，聚合模型的有功功率输出特性与详细模型基本一致。

由式(8)计算可得，工况一和工况二下算例1的等值误差分别为0.13%和0.50%，算例2的等值误差分别为0.29%和0.33%。

图6 工况一输出功率

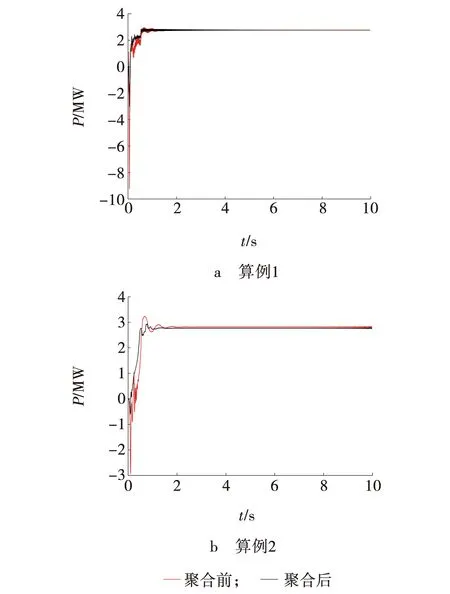
图7 工况二输出功率

4.1 同风速下

将工况一所述详细模型及聚合模型进行复转矩分析。可得到电气阻尼系数η如图8所示。

图8 工况一下阻尼特性

根据复转矩系数分析法判断系统次同步振荡的原理，当系统的电气弹性系数Ke与机械弹性系数Km之和为零时，此时电气阻尼系数Ke和机械阻尼系数Km之和小于零则可判断系统有次同步振荡风险。由于电气弹性系数Ke较机械弹性系数Km小很多，因此可以忽略电气弹性系数，仅考虑Km=0时的频率点，也就是发电系轴系的模态频率。由于机组的机械阻尼的计算较为复杂，而且会随负荷的变化而变化，通常以现场测量的方式来确定。在实际情况中，机械阻尼系数通常为不大的正值，因此在考虑一定裕度的情况下通常只考虑电气阻尼的正负情况。

由图8可以看出，工况一下算例1和算例2的电气阻尼系数η均为负值，算例一聚合前后η最低值分别为-50.51、-46.36，算例二聚合前后η最低值为-54.01、-47.63。即聚合前的η值略低于聚合后，但是聚合前后η最低点对应的频率均为34.5 Hz，接近火电机组的第四模态频率(32.28 Hz)。

根据上述复转矩系数分析法的原理可知，聚合前后η在发电机轴系的模态频率附近小于零，可判断系统聚合前后均有发生频率为32 Hz的次同步振荡的风险。为了验证上述判断的正确性进行时域仿真分析，在系统运行第3 s在串补线路末端投入持续0.075 s的三相短路故障，可得到图9所示两低压缸间的转矩M对比图。

图9 工况一低压缸间转矩

通过分析可知算例1、2聚合前后均发生了频率为32 Hz的SSO，但聚合后振荡略有减弱和复转矩系数法结论一致，其中算例1、2的误差为4.66%、6.91%。

4.2 不同风速下

对算例1、2在情况二所述详细模型及聚合模型下进行复转矩分析，得到如图10所示电气阻尼系数η。可以看出算例1、2均在聚合后η有更小的负值，算例一聚合前后η最低点分别为-52.01、-48.51。算例二聚合前后η最低值分别为-47.22，-45.38。η最低点所对应的频率均为34.5 Hz。因此可判断系统存在发生频率为模态四的SSO的风险。为验证复转矩系数法的有效性，对系统进行时域仿真验证，在系统运行第3 s在串补线路末端投入持续0.075 s的三相短路故障，如图11所示。

图10 工况二下阻尼特性

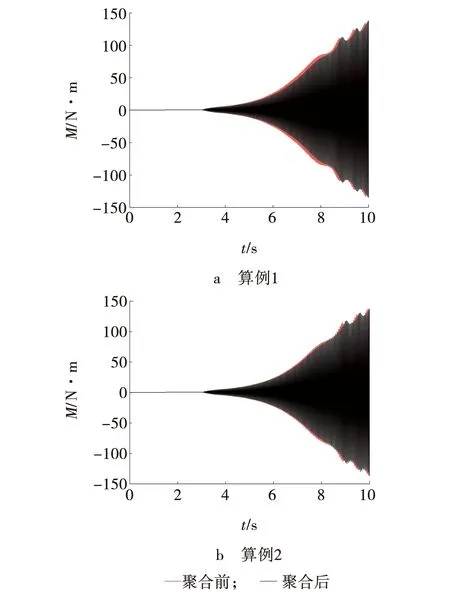
图11 工况二低压缸间转矩

由图11可见，两低压缸间的转矩对比图。通过分析计算可知聚合前后均发生频率为模态四的SSO，聚合前振荡较剧烈，算例1、2误差分别为4.36%、1.92%。

5 结 论

(1)理论推导了DFIG聚合对火电机组电气阻尼系数影响的表达式，小扰动下DFIG聚合前后输出ΔPg一致时，单机聚合对系统SSO无影响。

(2)风速相同的风机和风速不同的风机聚合前后得到的系统SSO频率一致，聚合未影响振荡频率。

(3)聚合前后，系统电气阻尼系数可能存在微小误差。但该误差不影响系统阻尼特性变化趋势，不影响系统阻尼特性分析，故可忽略不计。