一种低轨双星高脉冲重复频率雷达信号的定位模糊消除算法
姚山峰 贺 青 欧阳鑫信 杨宇翔
(盲信号处理国家级重点实验室 成都 610041)
1 引言
雷达与声呐系统中,针对运动目标为了取得较好的测速与杂波抑制性能,提高最大无模糊速度,通常发射高脉冲重复频率(High Pulse Repetition Frequency, HPRF)信号[1,2]。然而,当脉冲重复频率(Pulse Repetition Frequency, PRF)高到目标回波的传播时延大于发射的脉冲重复周期(Pulse Repetition Interval, PRI)时,将会产生距离模糊。类似地,在采用时差定位技术的无源定位系统中,当目标信号脉冲重复周期小于不同传输路径形成的到达时间差(Time Difference Of Arrival, TDOA)时,将产生时差模糊。高重复频率信号的模糊问题一直以来都是雷达与声呐系统中的研究热点,同样也是雷达信号无源定位领域的关键技术问题。
距离模糊与时差模糊本质上是由脉冲信号的周期重复性造成的。为了消除距离模糊,雷达与声呐系统中一般通过相位编码或变化重频的方式对发射脉冲串信号进行调制来区分不同脉冲的回波信号[3–8]。然而,对于第三方接收的无源定位系统来说,由于发射波形参数未知,无法对接收脉冲进行标记,这增加了模糊消除的难度。
目前,无源定位系统中针对高重复频率雷达信号采用的去模糊方法主要有去除模糊时差与去除虚假定位两类。第1类去除模糊时差的方法中,文献[9–11]提出结合测向信息,根据不同来波方向具有不同的脉冲到达顺序减少模糊配对的时差对。文献[12]利用无模糊的频差与频差变化率进行粗定位来消除时差模糊。这些方法要求对接收平台进行改造,增加高精度测向与测频差设备,这在已经发射入轨的天基平台上很难实现。文献[13]针对高重复频率的重复频率组变信号,提出一种参数相关脉冲配对法,在一定的参数分辨率要求下可有效地消除不同重频之间产生的模糊时差,但不能消除固定高重频信号自身周期性引起的模糊时差。文献[14]通过计算两个配对时差的相关系数与配对脉冲个数在时差配对环节消除了重复频率参差和重复频率组变两类信号子周期引起的模糊时差,不过对部分固定重频雷达信号,仍然存在虚假定位点。在第2类去除虚假定位点的方法中,文献[15]提出利用发散性去除虚假定位点,不过在积累时间内有可能存在位置发散不明显的多个定位点,此时将无法去除定位模糊[11]。文献[16,17]根据目标与接收站之间相对距离变化将对脉冲到达时间产生微量调制的规律,利用真实定位点的径向偏移应与脉冲到达时间的微量调制相吻合的特征剔除虚假的模糊航迹,这种方法对脉冲到达时间的测量精度与径向速度大小有较高的要求[17],限制了该方法的实际工程应用。
低轨双星定位技术凭借其瞬时覆盖范围大、定位精度高、卫星姿态要求低等优点,已成为目标侦察监视的一种重要手段[18]。本文针对低轨双星时差定位系统中高重频雷达信号的定位模糊问题,根据高速运动的低轨双星系统中不同位置的目标辐射源具有不同的时差变化特性,利用真实定位点的时差变化曲线与测量时差线变化规律相同,而虚假定位点的时差变化曲线却与测量时差线变化规律不同的原理,提出了一种基于时差变化趋势匹配(Variation Trendline Matching of TDOA, VTMT)的定位模糊消除算法。仿真结果表明,本文算法能够有效消除低轨双星时差定位系统中高重复频率雷达信号的定位模糊,显著提高无模糊定位概率,减小对时差测量精度与观测时间的要求。
2 模糊特性分析与现有定位模糊消除方法

图1中,红色虚线为根据卫星星历与校验台位置计算得到的无模糊理论时差变化曲线,蓝色圆点为测量时差值。可以看出,由于信号脉冲重复周期小于最大时差值,测量时差值位于13根时差线上,除了模糊数为0 的无模糊时差线以外,还在TDOA(t)−nTr(其 中n ∈{−7,−6,···,−1,+1,+2,···,+5})共计12根时差线上存在模糊的时差估计值。除此之外,还可以看出,各条模糊时差线与理论时差线具有相同的变化规律,只是在纵轴上距离相差整数倍的脉冲重复周期。
(2) 定位模糊分析:在只能测得目标信号时差的条件下,低轨双星系统一般采用分时时差定位体制实现目标辐射源的定位,定位方程组为
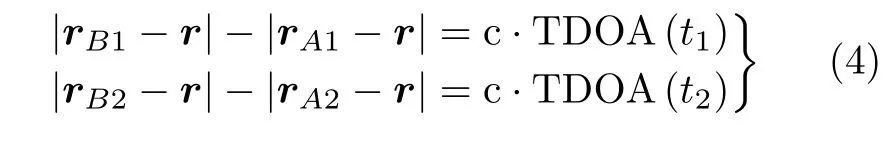
式中, r 为辐射源位置矢量,rAi=[xaiyaizai]T,rBi=[xbiybizbi]T分别表示A和B两颗卫星在第i (i =1,2 )时刻的位置矢量,T DOA(ti)表 示第i时刻的时差。
图2给出了图1中0 s与30 s时所有模糊时差值与地球表面相交的时差位置线(Line Of Position,LOP)。从图2可以看出,利用两个时刻的所有模糊时差值进行分时时差定位,除了两个时刻的无模糊时差位置线相交于目标真实位置处以外,所有的模糊时差位置线之间也会相交产生虚假的定位结果,如图2中的“×”形相交点。实际工程应用中,低轨双星系统一般通过左右接收通道区分基线两侧的目标,因此图2中只绘制了左侧区域的所有位置线交点。
另一种定位思路是利用低轨双星瞬时测量时差值与间隔一定时间以后的时差变化量联立定位方程组求解目标位置,如式(5)所示。将分时时差定位方程组式(4)中的第2个时差方程更改为时差变化量方程的好处在于,可以避免两个时差分别为不同模糊数时的虚假定位问题,但是两个相同模糊数的时差产生的虚假定位点仍然存在
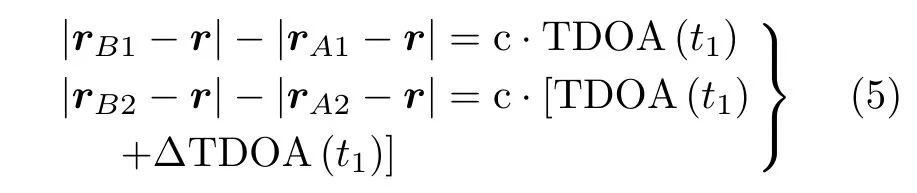
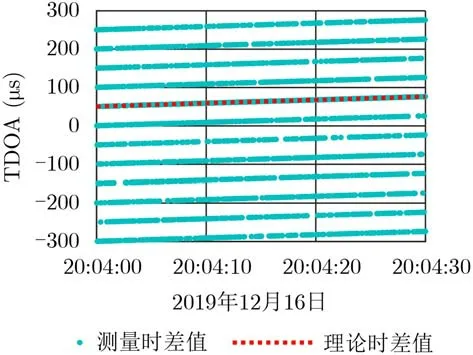
图1 时差周期模糊示意图
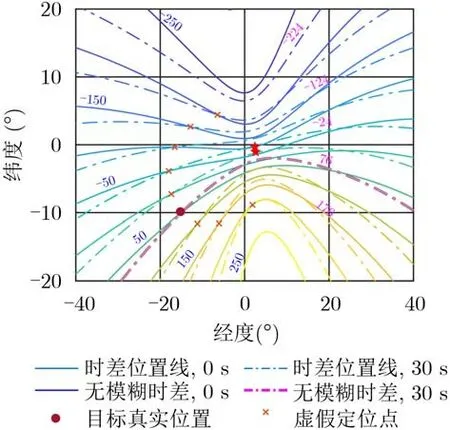
图2 分时时差定位模糊示意图

其中, TDOAn(t) 表示模糊数为n 的时差。此时,定位方程组在地球表面的位置线如图3所示。
与图2类似,时差位置线与时差变化量位置线将在多个位置相交,绝大多数交点都是模糊时差位置线产生的虚假定位点。直接利用模糊的时差估计结果进行目标定位,将得到虚假的定位结果。为了便于直观地对比不同重频时的定位模糊情况,图4中给出了重复频率提高到50 kHz时的定位模糊示意图。对比图3、图4可知,脉冲重复频率越高,虚假定位点越多,虚假定位点越靠近目标真实位置,虚假定位点的消除也就越困难。
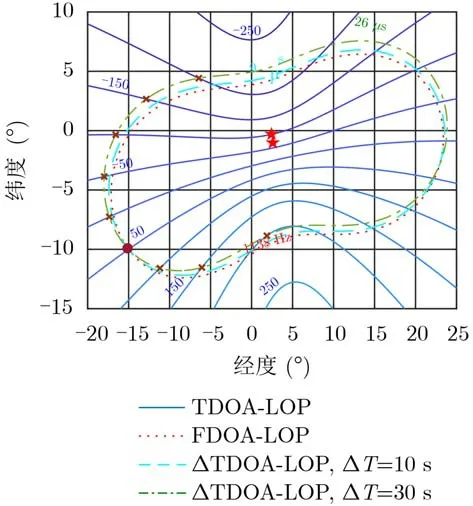
图3 时差/时差变化率定位模糊示意图(重频为20 kHz)
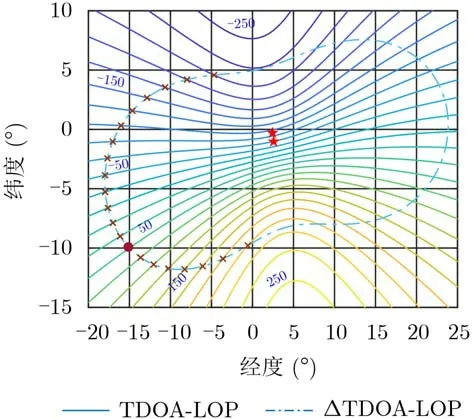
图4 定位模糊示意图(重复频率50 kHz)
(3) 利用虚假定位发射特性的定位模糊消除方法:对于脉冲重复周期过低(重频过高)形成的定位模糊问题,消除定位模糊的途径主要有增加测量信息[9–12]、多次测量数据分析处理[13–17]等。在天基无源时差定位系统中,目前主要采用的定位模糊消除方法是通过卫星多次测量的时差结果进行定位解算,利用虚假定位的发散特性去除模糊时差求得的定位点[15]。这种基于虚假定位点发散特性的虚假定位消除方法(Ghost Elimination Based on Divergence,GEBD)依据真实目标位置数据在短时间内不可能突变,而虚假定位点位置逐渐发散的原理,对每个定位点累积一定时间的定位结果,根据定位点的均方差变化情况对定位点的发散程度进行检测,将发散情况明显的定位点逐一去除,直至最后一个,则为真实定位点。而对于极高重复频率的目标辐射源,虚假定位点与真实位置相距很近,在积累时间内虚假定位点位置发散有可能不明显,此时无法有效去除虚假定位[11]。
重复频率分别为20 kHz与50 kHz,积累时间为30 s,时差测量精度为50 ns时,所有定位点的均方根误差(Root Mean Square Error, RMSE)如图5所示。
从图5可以看出,重复频率为20 kHz时,模糊数为0处取得最小均方根误差,这意味着,通过定位点的均方根误差可以从所有定位点中分辨出真实位置。重复频率为50 kHz时,模糊数为–1处的均方根误差小于真实位置处均方根误差,图6给出了此时定位求解得到的所有定位点。此时,利用虚假发散定位去除法将去除真实位置,保留模糊数为–1处的虚假定位点。
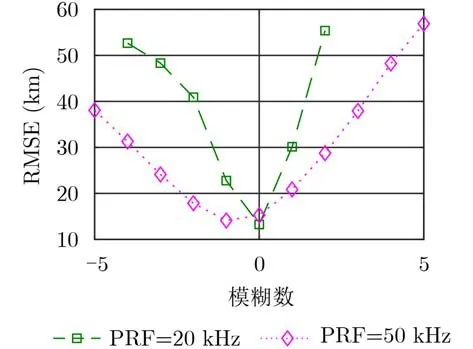
图5 所有定位点均方根误差变化曲线
3 利用时差变化特性消除定位模糊
低轨双星定位系统中,两颗卫星按照预定轨道相距一定距离同轨运行。在卫星过境时间内,双星接收到特定位置目标辐射源信号到达两颗卫星之间时差将根据目标与双星之间相对位置的变化发生改变。图7给出了某次过境时卫星覆盖区域内多个典型位置的时差变化曲线。
可以看出,不同位置的目标辐射源具有不同的时差变化曲线。本文正是利用不同位置目标辐射源具有不同的时差变化特性来实现定位模糊的消除与真实位置的判别。如前所述,所有的模糊时差线与无模糊时差线具有相同的变化规律,然而利用模糊时差线求解出的虚假定位点的时差变化曲线却与无模糊时差线有着不同的变化规律。于是,利用时差变化特性消除定位模糊的基本思想就是,通过计算给出定位点的测量时差线与该定位点的理论时差变化曲线的相似程度,匹配出测量时差线与理论时差线最为接近的定位点,该定位点即认为是对目标所处位置的估计。
所有时差估计值中,模糊数为 n的 M个时差
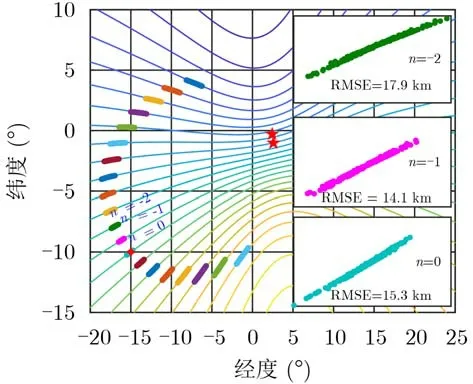
图6 所有定位结果分布图(重复频率50 kHz)
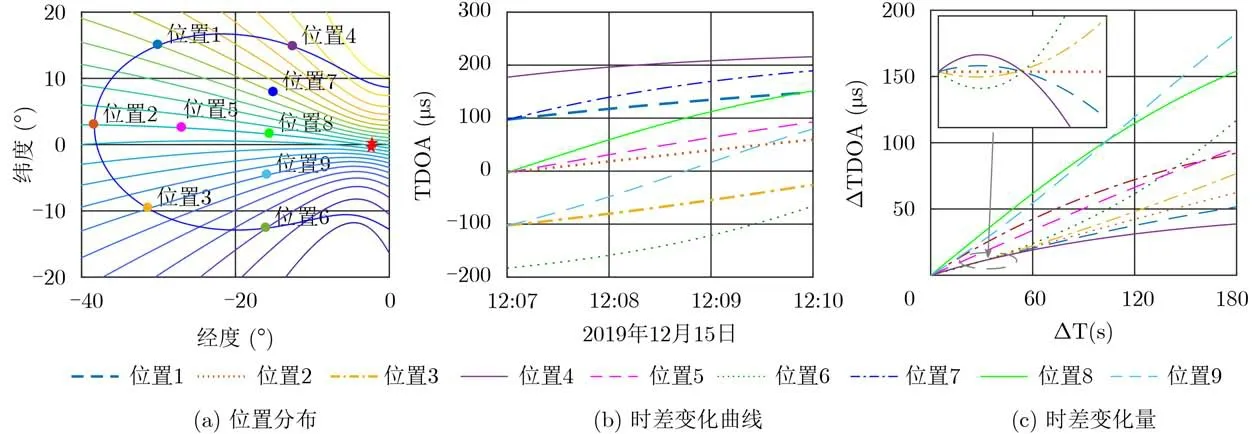
图7 理论时差变化曲线

式中,c ard(·)表 示求取集合基数,ε 为判别门限。
实际测量的时差值中,不同的模糊数对应着不同的时差点数,甚至可能出现有的模糊数没有一个时差估计值的情况。当这种现象发生在模糊数为0时,就意味着所有的定位结果中没有一个是目标真实位置。为了增大每个模糊数的时差点数,避免遗漏掉没有时差点的模糊数,可以将模糊数不同的时差估计值通过式(14)搬移到相同的模糊数下
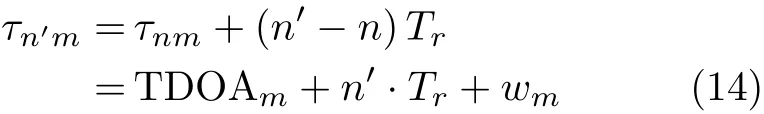
4 数据验证与性能分析
本节首先利用实际采集的校验台测试信号验证算法的有效性,然后再通过蒙特卡洛仿真分析脉冲重复频率、时差测量精度、观测时间长度、目标位置等参数对算法性能的影响。
(1) 校验台实采数据验证:在算法有效性验证试验中,分别采用虚假发散定位去除法与时差变化趋势匹配法对2019年12月17日某一轨卫星过境时实际采集的校验台测试信号进行定位处理,脉冲重复频率为50 kHz。低轨双星系统测量到校验台测试信号的原始时差结果如图8所示。
不同模糊数时差线得到的定位结果均方根误差以及理论时差线与各条模糊时差线之间的均方根误差如图9所示。可以看出,定位点均方根误差在模糊数为1时最小,于是利用定位点均方根误差作为发散度的虚假发散定位去除法无法给出校验台的真实位置。时差线均方根误差在模糊数为0时取得最小值,于是,本文算法能够从图8所示的29根模糊线中找出无模糊的时差线,有效地消除测试信号的定位模糊。
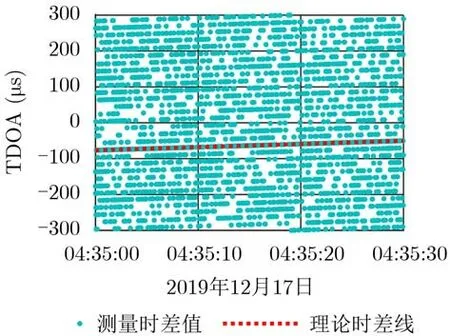
图8 重复频率50 kHz校验台信号时差估计结果
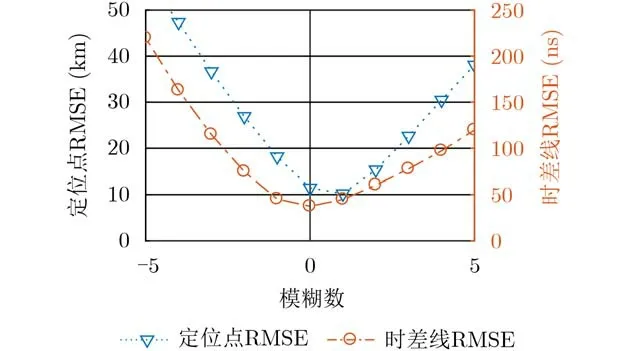
图9 两种算法不同模糊数的RMSE比较
(2) 性能仿真分析:下面通过仿真进一步分析本文算法的性能,其中,蒙特卡洛仿真次数为2000次,卫星轨道参数不变。
首先仿真分析时差测量精度对算法性能的影响。仿真中,假设目标辐射源位于图7中的1号位置,观测时间长度为30 s,时差测量误差分别为10 ns, 30 ns, 50 ns和100 ns时,无模糊定位概率随着重频的变化曲线如图10所示。可以看出,无模糊定位概率随着重频的增加而减小;时差测量误差越小,无模糊定位概率越高。除此之外,在仿真的几种时差测量精度下,本文算法性能均优于虚假发散定位去除法。
图11给出了不同观测时间长度下的无模糊定位性能曲线。仿真参数设置如下:时差测量精度为系统典型指标30 ns,观测时间长度分别为20 s, 30 s,60 s和120 s,目标位置保持不变。
图11表明,在仿真的几种观测时间长度下,本文算法性能均优于虚假发散定位去除法;观测时间长度越长,无模糊定位概率越高;对相同的重频,实现无模糊定位本文算法所需观测时间更短。与可以对感兴趣区域进行长时间凝视的高轨卫星不同,低轨卫星过境时间短,不可能在有限的过境时间内对某个目标进行长时间的观测,因此减小观测时间在实际应用中具有一定的工程价值。
时差测量精度设置为30 ns,观测时间长度为30 s。各个位置的无模糊定位概率曲线如图12所示。
从图12可以看出,在仿真的所有9个典型位置中,本文算法的无模糊定位概率均有明显的提升;当脉冲重复频率为100 kHz时,本文算法的无模糊定位概率提升量为15%~57%;在定位性能最好的8号位置处,本文算法将无模糊定位的最大重频从50 kHz提高到了200 kHz。
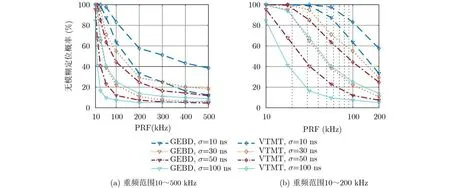
图10 不同时差测量精度下的定位模糊消除性能
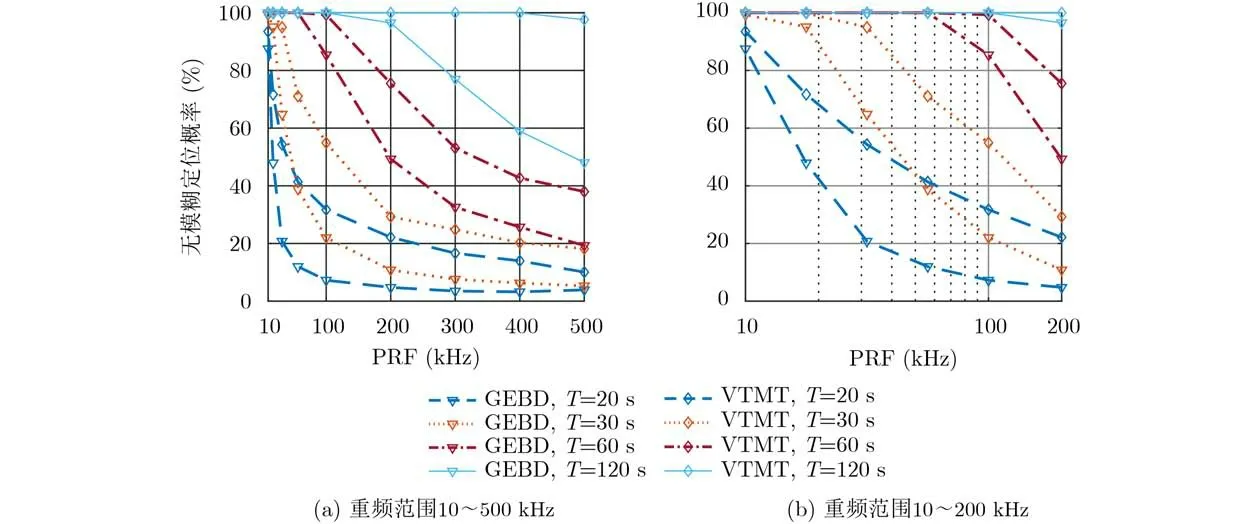
图11 不同观测时长下的定位模糊消除性能
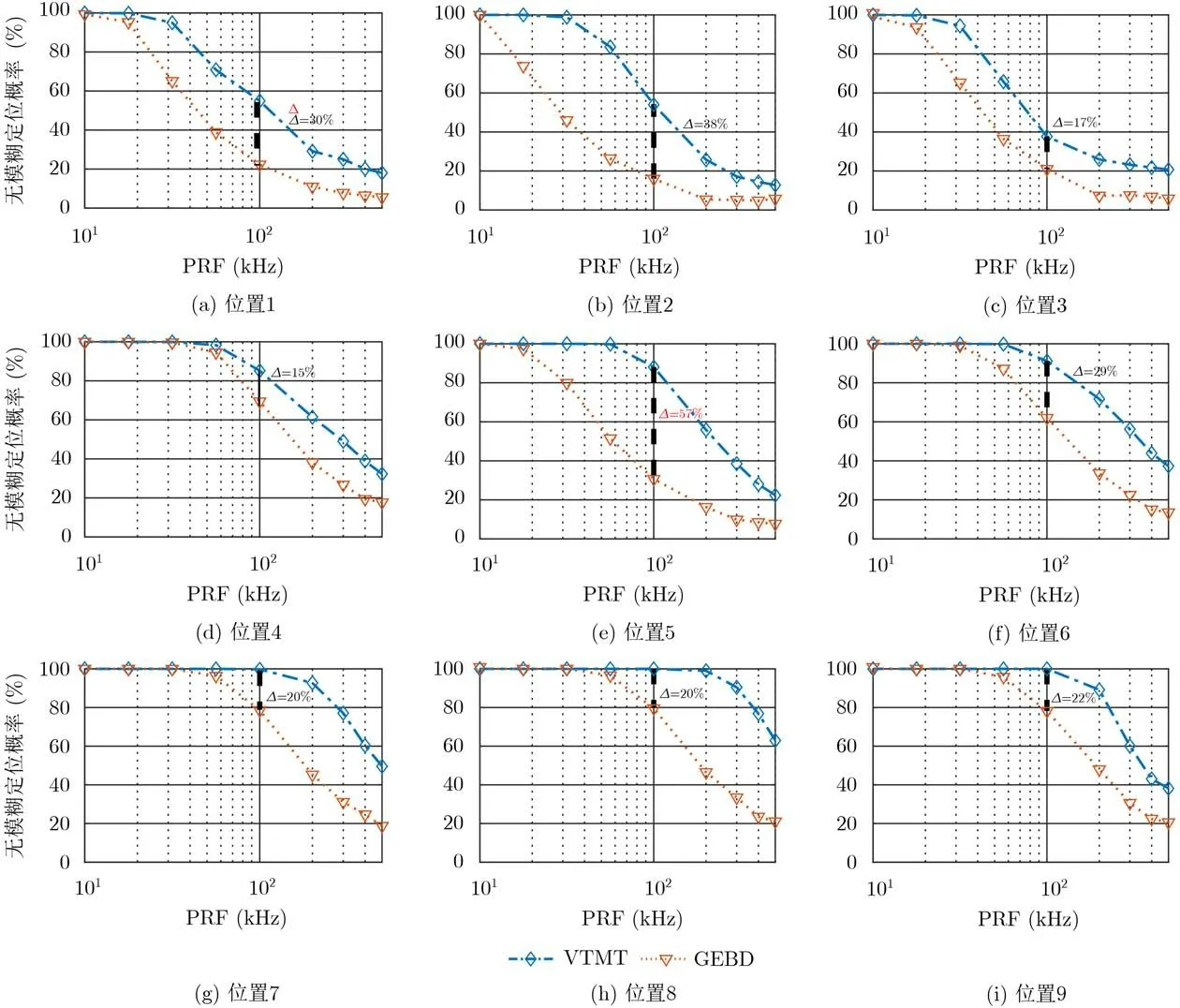
图12 不同位置的无模糊定位概率曲线
5 结束语
低轨双星系统中,卫星高速运动导致低轨双星与地球表面目标辐射源之间的相对几何关系在卫星过境时间内不断变化,于是,目标信号到达两颗卫星的时间差将随时间变化。根据不同位置的目标辐射源具有不同的时差变化趋势,本文提出了一种所有模糊时差序列与理论时差序列变化趋势匹配的高重频雷达信号定位模糊消除算法。实际采集的校验台测试信号验证了本文算法的有效性。仿真结果表明,在相同的时差测量精度与观测时间长度条件下,本文算法性能优于目前主要采用的虚假发散定位去除法。本文算法能够显著提高低轨双星时差定位系统中高重频雷达信号的无模糊定位概率,减小对时差测量精度与观测时间的要求,具有较高的应用价值,有利于提升低轨双星时差定位系统对高重频雷达信号的定位性能。

