黑龙江省耕地压力指数分析及趋势预测

金 鑫，李维刚

（1.佳木斯大学经济与管理学院，黑龙江 佳木斯154007；2.东北农业大学工程学院，哈尔滨150030）

粮食问题事关国运昌盛和百姓民生，粮食安全是国家安全的重要基础和保障[1]，与耕地安全密切相关。当前，我国耕地面临数量减少和质量下降双重挑战[2-3]，耕地保护压力较大，直接影响粮食安全。因此，“十三五”规划建议提出“坚持最严格的耕地保护制度，坚守耕地红线，实施藏粮于地战略”。黑龙江省地广人稀，耕地资源丰富，粮食产量较高，保证本省粮食供给能力强。但作为全国的粮食主产区、国家重要的商品粮基地和粮食战略后备基地，黑龙江省还肩负“中华大粮仓”和保障国家粮食供给重任。因此，测算和预测黑龙江省耕地压力指数，分析其耕地压力情况，将有助于实现耕地合理利用及粮食生产安排，为保障国家粮食安全作出贡献。学者从不同角度开展相关研究。余振国等研究我国粮食安全与耕地数量和质量关系[4]。张国等研究我国耕地中突出问题并分析其成因[5]。朱莉芬等利用计量经济模型开展城镇化对耕地影响的实证研究[6]。张乐勤等运用边际模型研究城镇化演进对耕地影响极限[7]。徐明岗等研究我国耕地质量状况与提升对策，指出耕地质量整体偏低、退化和污染严重、占优补劣现象普遍[8]。蔡运龙等提出通过耕地压力指数反映耕地资源与粮食安全之间关系，将耕地资源数量、耕地质量、人口数量、粮食产量等指标与粮食需求结合[9]。罗翔等引入耕地生产力标准系数对蔡运龙等提出的耕地压力指数模型作修正[10]。喻保华对河南省耕地压力指数进行动态分析和预测[11]。亚森江·喀哈尔等运用最小人均耕地面积和耕地压力指数模型定量分析新疆粮食安全程度[12]。目前，相关研究仅考虑本地区内部压力，忽视粮食贸易流通带来的外部压力。因此，本文借助贸易引力模型思想提出耕地外部压力指数模型，将其与修正后的内部压力指数模型结合以构建耕地综合压力指数模型。运用改进后模型对黑龙江省开展实证分析，并利用灰色GM(1,1)模型和残差序列修正后模型预测黑龙江省耕地综合压力指数，分析黑龙江省耕地压力情况。

1 耕地压力指数模型改进

1.1 传统耕地压力指数模型

耕地压力指数是衡量一个地区在满足粮食生产情况下耕地可利用紧张程度的重要指标。传统耕地压力指数实际上是最小人均耕地面积与实际人均耕地面积比值[9-10]。公式为：

式中，K为传统耕地压力指数；Smin为最小人均耕地面积；Sa为实际人均耕地面积。

最小人均耕地面积是指在某一地区范围内，为满足该地区范围内每人维持正常生活粮食消费需求所需的耕地面积[9-10]。最小人均耕地面积计算公式如下：

式中，β为粮食自给率；Gr为人均年粮食需求量；p为粮食单产；q为粮食播种面积占总播种面积比重；k为复种指数。

在这一传统耕地压力指数模型中，仅考虑该地区人均耕地面积情况，认为K=1时，Sa=Smin，实际人均耕地面积等于最小人均耕地面积，即该地区耕地压力达临界值。当K＞1时，Sa＜Smin，即实际人均耕地面积小于最小人均耕地面积，说明该地区耕地压力已突破临界值，粮食供给能力已无法满足当地居民粮食需求，粮食安全受威胁。当K＜1时，Sa＞Smin，即实际人均耕地面积大于最小人均耕地面积，该地区耕地压力尚未达到临界值，说明粮食供给能力大于当地居民的粮食需求，此时适当休耕轮作，增加耕地的地力[11-12]。

1.2 耕地压力指数模型的改进

通过分析传统耕地压力指数模型发现，粮食自给率无相应的统计数据，以往研究大多为主观取值，产粮大省设定为100%，粮食进口大省则设定为50%。取值不利于准确计算耕地压力指数[13]。因此，改进耕地压力指数模型中不宜采用粮食自给率变量。传统耕地压力指数模型去除粮食自给率变量后，实际就是耕地内部压力指数，KI表示，公式为：

通过传统模型测算耕地压力指数，主要分析当地粮食供给与粮食需求关系，传统模型主要体现耕地受到本地区的内部压力。但随着粮食贸易发展，某地区粮食生产不仅满足当地居民消费需要，还通过贸易手段解决其他地区的粮食需求，耕地受外部地区粮食需求压力，即耕地外部压力影响。传统耕地压力指数模型仅考虑某一地区内部情况，无法反映当前粮食需求压力，应运用外部压力指数替代粮食自给率。本研究为综合考虑某一地区区域内外粮食需求情况，需改进传统耕地压力指数模型，改进后的耕地压力指数模型中同时考虑耕地内外部压力。

耕地外部压力指数模型构建可参考和借鉴贸易引力模型。贸易引力模型思想来源于牛顿万有引力定律，主要用于分析双边贸易流量[14-15]。借鉴贸易引力模型的思想和理论，对黑龙江省和我国其他地区作为粮食贸易双边对象，提出粮食获取能力这一变量，是某地区对其他地区粮食供给的吸引力。根据贸易引力模型理论，引入人均GDP和人均收入变量，粮食获取能力计算公式如下：

式中，θ为粮食获取能力；xi为第i个地区人均GDP；xˉ为其他地区人均GDP平均值；yi为第i个地区人均收入；yˉ为其他地区人均收入平均值。

当某地区的粮食获取能力较强时，可从外部获取粮食满足本地区粮食消费需求，减轻对本地区耕地的压力。反之，如果当地粮食获取能力较弱时，粮食就易流向获取能力强地区，而减少对本地居民供应，其他地区对本地区耕地构成外部压力。可见，某地区耕地外部压力与其粮食获取能力呈反比。因此，耕地外部压力指数表示为KO，公式为：

本研究所改进耕地压力指数模型综合耕地内外部双重压力。改进后模型表示为如下公式：

式中，K为耕地综合压力指数；KI为耕地内部压力指数；KO为耕地外部压力指数；Smin为最小人均耕地面积；Gr为人均年粮食需求量；p为粮食单产；q为粮食播种面积占总播种面积比重；k为复种指数；θ为粮食获取能力；xi为第i个地区人均GDP；xˉ为其他地区人均GDP平均值；yi为第i个地区人均收入；yˉ为其他地区人均收入平均值。

2 黑龙江省耕地综合压力指数测算

2.1 数据来源

为测算和分析黑龙江省耕地综合压力指数变化情况，需收集和计算式（6）中各项指标数值。本文数据来源于2005～2018年《黑龙江统计年鉴》、《中国粮食年鉴》和《国家统计局关于2018年粮食产量数据的公告》[16-18]。搜集和计算2005～2018年各项指标数值如表1所示。

根据表1中黑龙江省2005～2018年人口数变化情况，绘制黑龙江省人口数和人口自然增长率曲线，如图1所示。

表1 2005～2018年黑龙江省各项指标数值Table 1 Indices of Heilongjiang Province during 2005-2018

图1 2005～2018年黑龙江省人口数与人口自然增长率Fig.1 Population and natural growth rate of Heilongjiang Province during 2005-2018

由图1可知，2005～2013年黑龙江省人口数呈较为稳定增长，2014年开始出现较大幅度人口减少。人口自然增长率虽个别年份出现较小幅度上升，但从长期趋势看呈较大降幅。具体来说，2005～2018年全国人口自然增长率从5.89‰微降至3.81‰，处于平稳态势。而同期黑龙江省人口自然增长率已从2.67‰降至-0.69‰。无论从人口数还是人口自然增长率来看，黑龙江省近几年均呈下降趋势，且该趋势在一定时期内仍将延续。由于耕地综合压力指数模型中无论是内部压力指数还是外部压力指数均受到人口数变化影响，因此，黑龙江省人口数及自然增长率下降趋势，势必对耕地综合压力指数产生重要影响。

2.2 耕地外部压力指数测算

为更好反映黑龙江省粮食获取能力和耕地外部压力指数变化情况，将2005～2018年黑龙江省和全国人均GDP及人均收入数据搜集和整理后，计算黑龙江省外全国其他地区人均GDP和人均收入。并根据公式（4）和（5）计算得出黑龙江省各年份粮食获取能力和耕地外部压力指数，相关数据如表2所示。

根据表2数据绘制黑龙江省及全国其他地区的人均GDP、人均收入和黑龙江省粮食获取能力及耕地外部压力指数变化曲线，如图2～4所示。

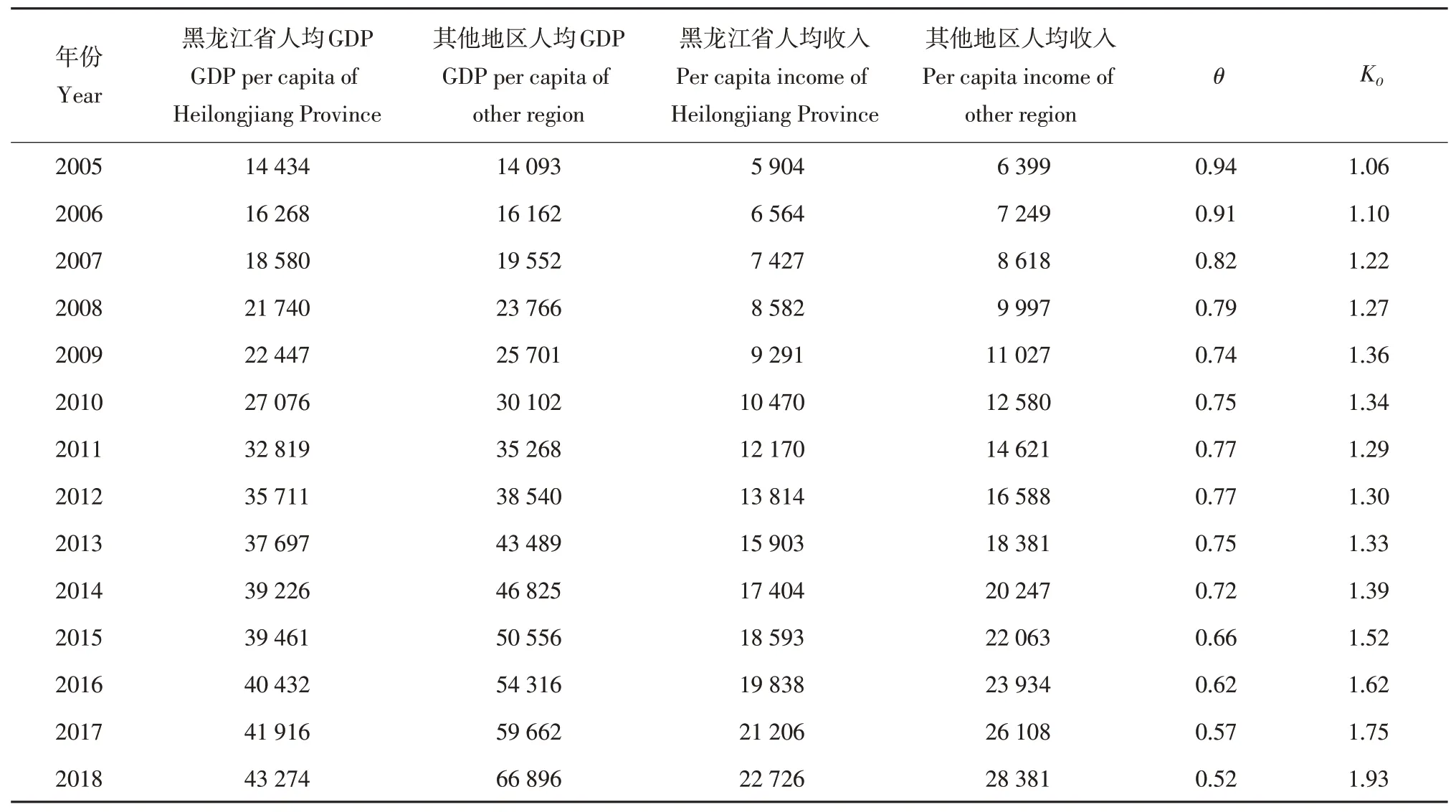
表2 黑龙江省历年粮食获取能力及耕地外部压力指数Table 2 Grain gain capability and arable land external pressure index of Heilongjiang Province

图2 2005～2018年黑龙江省和全国其他地区人均GDPFig.2 GDP per capita of Heilongjiang Province and other region during 2005-2018

图3 2005～2018年黑龙江省和全国其他地区人均收入Fig.3 Per capita income of Heilongjiang Province and other region during 2005-2018

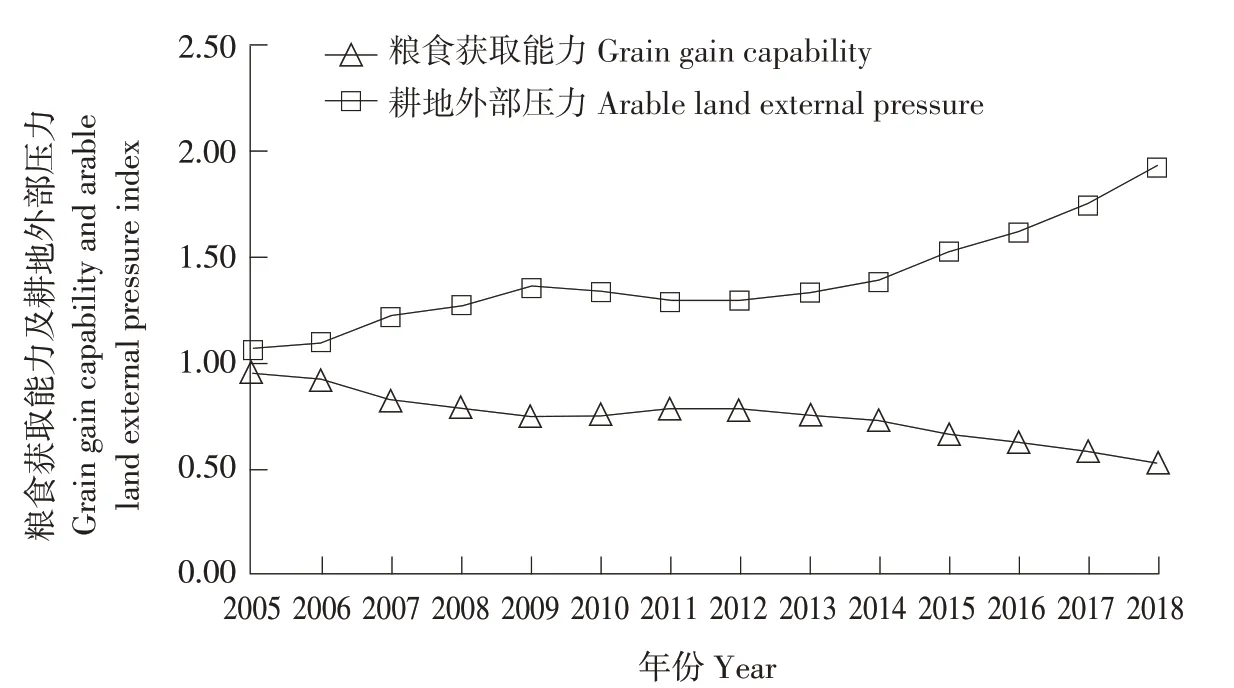
图4 2005～2018年黑龙江省粮食获取能力和耕地外部压力指数Fig.4 Grain gain capability and arable land external pressure index of Heilongjiang Province during 2005-2018

由表2可知，2005年黑龙江省人均GDP略高于全国其他地区341元，人均收入略少于全国其他地区495元，但这与全国其他地区相近。而到2018年，黑龙江省人均GDP为2005年3倍，全国其他地区则为4.75倍，全国其他地区超过黑龙江省23 622元。人均收入变化方面，2018年全国其他地区人均收入已达28 381元，为2005年4.44倍，黑龙江省则是3.85倍，黑龙江省少于全国其他地区5 655元。由图2～3可知，14年间黑龙江省人均GDP和人均收入两项指标增速远低于全国其他地区，截至2018年两项指标均落后于全国其他地区。此外，图4中黑龙江省粮食获取能力由0.94降至0.52，下降幅度达44.68%。同期耕地外部压力指数由1.06升至1.93，上升幅度达82.08%。

2.3 耕地内部压力指数测算

为测算黑龙江省耕地内部压力指数，需根据表1中指标数值计算黑龙江省各年粮食单产p、粮食播种面积占总播种面积比重q、复种指数k。各指标数值计算结果如表3所示。

表3 2005～2018年黑龙江省各项指标数值Table 3 Relevant indices of Heilongjiang Province during 2005-2018

然后，确定人均年粮食需求量Gr。《国家粮食安全中长期规划纲要（2008-2020年）》指出，2010年我国居民人均粮食消费量为389 kg，2020年人均粮食消费量为395 kg。而唐华俊从考虑居民营养健康角度，测算出基于平衡膳食模式下中国人均粮食需求量，低方案为252.64 kg，中方案为322.07 kg，高方案为386.60 kg。可认为人均粮食需求量为322.07 kg，基本满足我国人均粮食安全的需求量，粮食人均占有量为386.60 kg时，即可确保我国粮食安全。近年来，我国实际人均粮食消费量在378.88～406.09 kg范围波动[19]。结合我国百姓实际粮食消费量和唐华俊测量结果，本研究将人均粮食需求量Gr分别取值为322、386和400 kg。

最后，根据表3中3个变量数值以及前文所确定Gr的3种取值情况，分别计算最小人均耕地面积Smin，再根据表1中实际人均耕地面积Sa数值，按照式（3）计算得出耕地内部压力指数KI，结果见表4。

由表4可知，2005年时，当人均年粮食需求量取322 kg时，黑龙江省耕地内部压力指数为0.3980，而取值为400 kg时，内部压力指数达0.4944，但压力数值仍＜0.5，说明耕地内部压力处于较低水平。随着人口数减少、耕地面积增加、粮食单产提升、粮食播种面积比重增加，黑龙江省耕地内部压力指数进一步降至2018年0.2022，为2005年41%。黑龙江省耕地内部压力指数变化见图5。

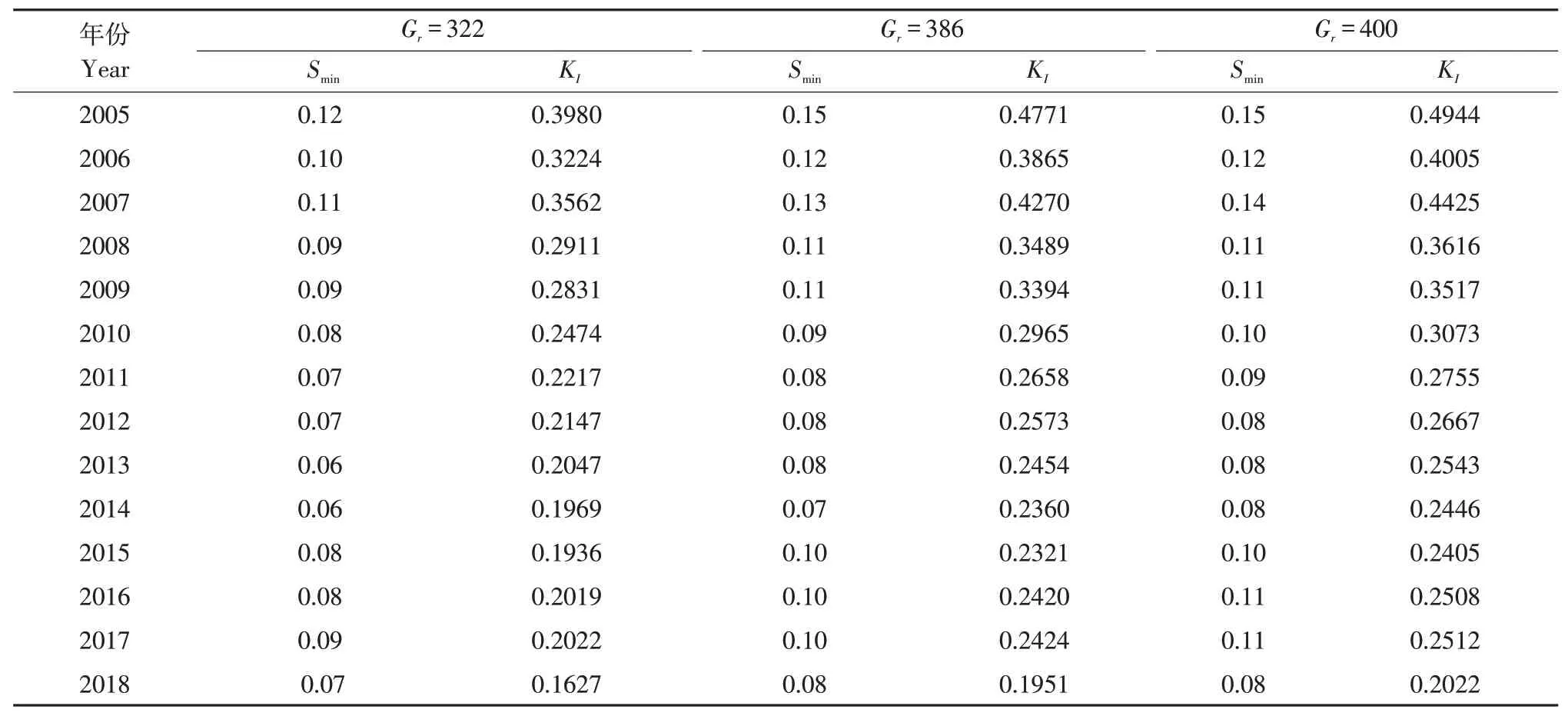
表4 黑龙江省历年最小人均耕地面积和耕地内部压力指数Table 4 Smin and KI of Heilongjiang Province during 2005-2018

图5 2005～2018年黑龙江省耕地内部压力指数Fig.5 Arable land internal pressure index of Heilongjiang Province during 2005-2018

2.4 耕地综合压力指数测算

根据表2中的耕地外部压力指数和表4中的耕地内部压力指数，运用公式（6）可得出2005～2018年黑龙江省耕地综合压力指数，计算结果如表5所示。以人均年粮食需求量Gr取400 kg为例，绘制黑龙江省耕地的内外部及综合压力指数折线图，如图6所示。可知，2005～2018年黑龙江省耕地外部压力持续加大，而同期的耕地内部压力则在不断减弱。受耕地内外部压力的双重影响，黑龙江省耕地综合压力基本呈现下降趋势。

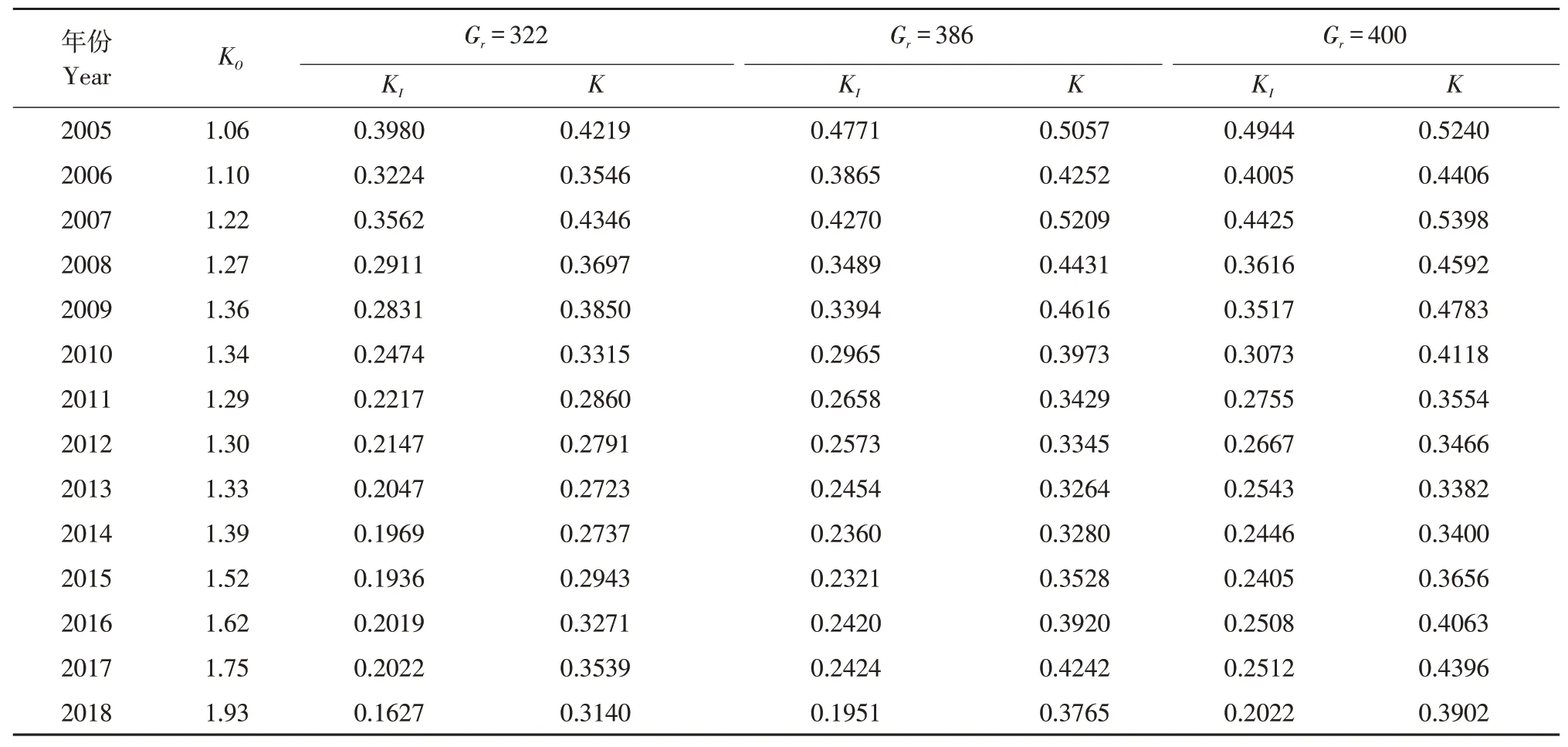
表5 2005～2018年黑龙江省耕地综合压力指数Table 5 Arable land comprehensive pressure index of Heilongjiang Province during 2005-2018

图6 2005～2018年黑龙江省耕地压力指数Fig.6 Arable land pressure indexes of Heilongjiang Province during 2005-2018

3 黑龙江省耕地压力指数预测分析

由于耕地压力指数模型中所涉及各项指标具有不确定性，即“灰色”性。尽管过程中所显示现象是随机、杂乱的，但仍有一定边界性，且呈有序性。针对这种指标数值表现规律性，可运用灰色系统理论思想建立相应灰色模型，并对各指标分别作灰色预测。而灰色理论中GM（1,1）模型由于适用于小样本且易于求解，广泛应用于工业、农业、经济及生物学等领域[20]。为更好预测和反映黑龙江省耕地压力指数动态变化情况，本文采用灰色GM（1,1）预测模型对实际人均耕地面积Sa、粮食单产p、粮食获取能力θ和复种指数k分别展开预测。预测精度直接影响预测结果有效性，因此在构建GM（1,1）预测模型时，如预测精度良好，可直接用该模型预测相应变量；而当预测精度低时，则可运用相比原模型精度更高的灰色GM（1,1）残差模型修正原模型，实现更高精度预测[21-22]。

3.1 实际人均耕地面积预测

按照灰色GM（1，1）预测模型求解步骤，可得出有关实际人均耕地面积Sa预测模型：

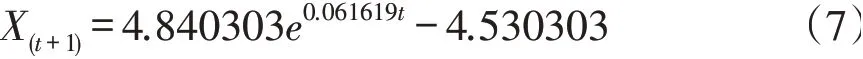
该预测模型后验比C=0.5128＞0.35，小概率误差P=0.7143＜0.95，可见预测精度较低。因此，运用GM（1,1）残差模型预测，得残差模型为：

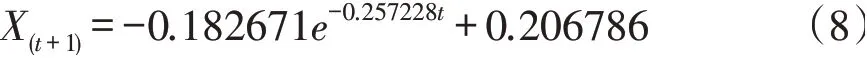
该预测模型后验比C=0.2470＜0.35，小概率误差P=1＞0.95。由此可知，预测精度较好，可利用修正后灰色GM（1，1）预测模型预测实际人均耕地面积Sa。

3.2 粮食单产预测

按照灰色GM（1,1）预测模型求解步骤，可得出有关粮食单产p预测模型：

该预测模型后验比C=0.7361＞0.35，小概率误差P=0.4286＜0.95，可见预测精度较低。因此，运用灰色GM（1，1）残差模型预测，得残差模型为：

该预测模型后验比C=0.1980＜0.35，小概率误差P=1＞0.95。由此可知，预测精度较好，可利用修正后灰色GM（1,1）预测模型预测粮食单产p。

3.3 外部压力指数预测

按照灰色GM（1,1）预测模型求解步骤，可得出有关外部压力指数KO预测模型：

该测模型后验比C=0.0871＜0.35，小概率误差P=1＞0.95，评价结果均为较好。由此可知，预测精度较好，可直接运用该传统灰色GM（1，1）预测模型来预测外部压力指数KO。

3.4 复种指数预测

按照灰色GM（1，1）预测模型求解步骤，可得出有关复种指数k预测模型：

该预测模型后验比C=0.8508＞0.35，小概率误差P=0.4286＜0.95，可见预测精度较低。因此，运用灰色GM（1,1）残差模型预测，得残差模型为：

该预测模型后验比C=0.1345＜0.35，小概率误差P=1＞0.95，评价结果均为较好。由此可知，预测精度较好，可利用修正后灰色GM（1，1）预测模型预测复种指数k。

3.5 人均年粮食需求量预测

近年黑龙江省人口呈“低出生率、低死亡率和低自然增长率”规律。另外，人口尤其青壮年净流出，儿童与老年人留守现象突出[23]。从人口增长情况和流动情况来看，黑龙江省人均年粮食需求量在未来几年内不会明显增长，维持在400 kg。

3.6 粮食播种面积占总播种面积之比预测

黑龙江省粮食播种面积占总播种面积之比已提升到2018年的97%。随着我省粮食生产在全国比重日益重要，该比值在未来短期内不会明显下降。因此，认为黑龙江省粮食播种面积占总播种面积之比在未来短期内维持97%。

根据改进后耕地压力指数模型，即公式（6），运用灰色GM（1,1）预测模型预测得到各变量值及耕地压力指数如表6所示。在图6基础上，提取关键因素绘制图7。

表6 2019～2023年耕地压力指数及相关变量值预测Table 6 Arable land pressure index and relevant variables of Heilongjiang Province during 2019-2023

图7 2019～2023年黑龙江省耕地压力预测Fig.7 Arable land pressure prediction of Heilongjiang Province during 2019-2023

4 结论与政策启示

4.1 结论

传统耕地压力指数模型仅反映某地区内部耕地压力，且模型中粮食自给率取值具有较强主观性。本研究借鉴贸易引力模型思想构建耕地外部压力指数模型，可较好反映由于粮食贸易产生的粮食需求和耕地外部压力，通过耕地综合压力指数模型全面反映耕地内外部双重压力。改进模型实证分析和预测结果表明，黑龙江省耕地内部压力较小，但外部压力较大，导致综合压力指数高于内部压力指数即传统模型计算结果，可有效警示耕地安全和粮食安全，避免耕地资源浪费及不合理利用。本研究提出的耕地外部压力指数模型仅选取人均GDP和人均收入两项指标，今后将对指标展开深入分析和探讨以完善耕地压力指数模型。

4.2 政策启示

①耕地内部压力及综合压力指数下降，应控制人口流失，扭转人口减少趋势。根据人口规模及耕地内部及综合压力测算和预测结果可知，黑龙江省耕地内部压力、综合压力指数及人口规模呈显著下降趋势，说明人地矛盾并不突出，黑龙江省人口增加有较大空间。因此，政府应扭转人口规模下行趋势，采取措施控制人口外流，吸引人才流入。

②耕地外部压力较大，应严格做好耕地保护工作。黑龙江省耕地外部压力测算和预测结果表明，外部压力呈上升趋势。为保障国家粮食安全，黑龙江省应充分保护好黑土地优质耕地资源，严禁耕地滥用，防止耕地资源浪费。充分挖掘后备耕地资源，做好土地资源储备，适当补充粮食耕地面积。除严格保护耕地数量外，黑龙江省可利用耕地综合压力减轻的缓冲期，在保证国家粮食安全供给前提下，合理测算可适度休耕或轮作的耕地面积，并以此开展科学的休耕轮作计划安排，恢复和提升地力，实现“藏粮于地”。

③粮食单产波动较大，应推进粮食生产现代化。从粮食单产历史数据看，虽整体呈上升趋势，但波动幅度大。除受气候和自然灾害影响外，粮食生产过程中科技化、现代化仍需提升。应加快农业科技和成果转化步伐，选育和引进良种。通过精准气象和灾害预警手段，调整粮食种植结构。加大无人机、数字传感器、大数据和人工智能等现代化科技手段为粮食生产服务，努力稳定和提升粮食单产，不断提高耕地生产力，实现“藏粮于技”。

④耕地面积与粮食播种占比已近上限，应加强跨境农业合作。从粮食播种面积在总播种面积占比和耕地面积变化情况看，播种面积占比已达97%，提升空间有限，休耕轮作制度则进一步限制耕地面积扩大。因此，可利用黑龙江省区位优势，加强与俄罗斯远东地区跨境农业合作，加快“走出去”步伐。有效推进我国粮食安全供给侧结构性改革，打造黑龙江省新经济增长极。