基于CST 仿真软件的阻抗匹配设计教学实验
廖 臻,廖志斌,刘宇平
(1. 杭州电子科技大学 电子信息学院,浙江 杭州 310018;2. 新余学院 数学与计算机学院,江西 新余 338000)
随着通信技术的蓬勃发展,社会对射频微波技术人才的需求也与日俱增[1-3]。为培养这类人才,电子信息学科已将电磁场与微波技术作为必修课程。传输线理论是设计射频微波电路的基础,它与传统电路理论有着很大不同。传统电路理论分析的前提是电路的物理尺寸度远小于电波长,然而传输线的尺寸通常与电波长相近。因此,传输线是分布参数网络,这一特点使得传输线理论中有阻抗匹配的概念,这是设计射频微波电路的基础。但是阻抗匹配分析在教材中主要通过数学公式来表达,概念十分抽象,学生很难对传输线的阻抗匹配有一个直观的认识[4-6]。因此,针对传输线阻抗匹配的实验环节将有助于学生掌握阻抗的概念以及匹配网络设计方法。但是,由于射频微波电路的加工很难在学校实验室中完成,同时微波测量需要昂贵的实验设备且实验操作复杂,这类实验很难在日常教学中推广。值得庆幸的是随着电磁仿真技术的发展,商用电磁仿真软件已经能够精确地模拟射频微波实验[7]。采用虚拟仿真实验不仅能够达到仪器测量的效果,而且还可以展示传输线内部的场分布,给使用者一个直观的感受[8-9]。
因此,我们在阻抗匹配相关课程中引入教学实验,采用理论分析和电磁仿真实验相结合的授课模式。本实验利用电磁仿真软件CST,构建了一个包括传输线阻抗分析、匹配网络设计和微带线仿真验证的完整的实验过程。在实验的实施过程中,将复杂的数学推导与直观的物理现象对应起来,加深学生对阻抗匹配的理解,并掌握匹配网络的设计方法。
1 传输线阻抗分析
传输线的阻抗是传输线理论的关键内容。教材中利用等效集总元件电路模型推导出端接负载的无耗传输线上的总电压、总电流方程分别为[10]:
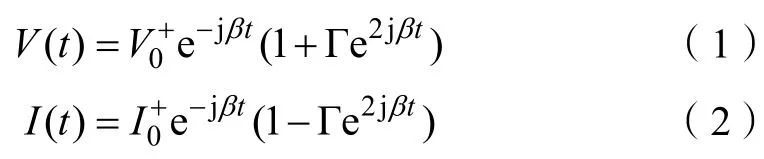
式中,为入射电压波的振幅,β为相位传播常数,t为负载与源之间的距离,Γ 为电压反射系数:

其中ZL为终端负载阻抗,Z0为传输线特性阻抗。
若负载阻抗与传输线阻抗匹配,ZL=Z0,则Γ=0,且传输线上的电压幅值|V(t)| = || 为常数。当负载失配时,传输线上的反射波会导致驻波,使得部分功率无法传给负载。同时,线上的电压幅值|V(t)|=|||1 +Γe2jβt|不再是常数,而是沿线随t起伏变化。在射频微波电路的实际工程中,经常会出现传输线与负载不匹配的情况。为了避免不必要的功率损耗,需要在负载和传输线之间设计阻抗匹配网络,使得向匹配网络看去的阻抗等于Z0。
2 阻抗匹配网络设计
阻抗匹配网络的设计方案通常有集总元件匹配、单支节短截线匹配、双支节短截线匹配以及1/4 波长变化器等。本文以单支节短截线匹配技术为例,进行设计学习。单支节短截线匹配网络使用单个开路或者短路的传输线段,在特定的位置与原有传输线并联或者串联,如图1 所示。从微波制造的观点看,这种匹配电路不需要集总元件,尤其是并联支节特别容易制成微带线的形式。
在单支节短截线匹配网络中可调参数包括:从负载到短截线的距离d和由短截线提供的电纳或电抗。其中对于并联短截线情况(见图1(a)),设计思路是选择合适的长度d,使其在距离负载d处向负载看去的导纳Y是Y0+jB形式。然后,在此处并列一个电纳为–jB的短截线以达到匹配条件。对于串联短截线情况(见图1(b)),同理选择合适的距离d,使其在距离负载d处向负载看去的阻抗Z具有Z0+jX形式,然后串联电抗为–jX的短截线,便达到匹配条件。
本实验以一个负载阻抗ZL=60–j80 Ω 为例,在3 GHz 时设计匹配网络,使负载与50 Ω 传输线匹配。匹配网络的设计拟采用单支节并联短截线的Smith 圆图解法。Smith 圆图是一种辅助图像工具,它提供了一个使传输线阻抗可视化的有效的方法,能够在不使用复杂数学公式的情况下,迅速和准确地设计匹配电路。从教学和工程的角度来说,Smith 圆图的掌握都是非常重要的[11]。
设计过程首先归一化负载阻抗并用zL表示,
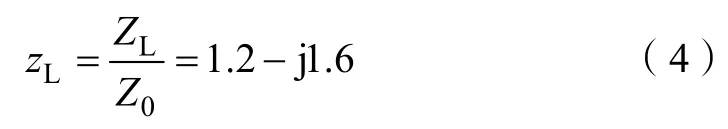

图2 阻抗匹配网络的Smith 圆图
并标在Smith 圆图中(见图2)。然后画出等反射系数圆,将归一化负载阻抗转换成归一化负载导纳yL,并将Smith 圆图考虑成导纳圆图。从图中可以看到,从归一化负载导纳yL沿着等反射系数圆向信号源方向(顺时针)旋转,会与匹配圆相交于y= 1 +j1.47点。这里旋转所经历的电长度就是负载到短截线的距离d。从图上角度标尺可以得出:
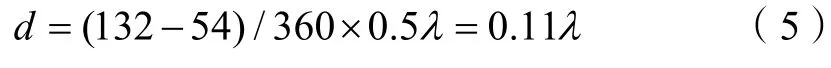
由此可以看出,并联匹配需要一个电纳为–j1.47的短截线。在圆图中标出该电纳位置,从短路点出发向信号源方向旋转到标识位置,旋转所经历的电长度对应该短截线的长度F。从圆图标尺可以读出:
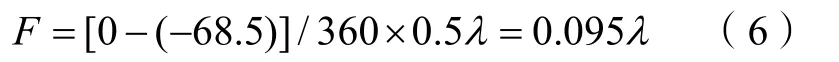
根据所得参数,设计的阻抗匹配网络如图3 所示。

图3 阻抗匹配网络
3 微带建模及电磁仿真实验
通过以上单支节短截线设计,可以使学生掌握阻抗匹配网络的设计方法,加深对传输线阻抗理论的理解。为了对所设计的匹配网络进行实验验证,使学生对传输线阻抗匹配有一个更直观的理解,利用CST 软件构建了没有匹配网络和有匹配网络的两种微带线模型(见图4),通过比较电场幅值分布和反射系数展示阻抗匹配的作用。
微带线的基底采用F4B 板材,相对介电常数εr=2.65,厚度h=1 mm。根据微带线经验公式,可以算出特性阻抗Z0=50 Ω 的微带线宽度为2.7 mm,等效介电常数εeff=2.18[11]。由此可得,3 GHz 时微带线上的波长为

根据以上所综合出的微带线参数,在CST 软件中建模,微带线长度为110 mm。模型中左侧为输入端口,右侧端面直接连接集总元件,如图4(a)所示。集总元件采用RLC串联结构,在3 GHz 时电阻R=60 Ω 和电感C=0.663 pF 的串联实现负载阻抗ZL=60–j80 Ω。图4(b)给出了3 GHz 时微带线上电场的幅值|E|分布。从中可以看出,电场的幅值沿着微带线波动,存在着波峰和波节,这说明了由于负载与微带线不匹配,存在反射波导致了驻波。
为了实现阻抗匹配,需要在负载和微带线之间设计阻抗匹配网络。结合上一节所得的阻抗匹配网络设置,在微带线的末端并联一段F=0.095λg=6.43 mm 的短截线。在短截线的末端通过过孔将基片与接地板相连。然后在并联支路与负载之间添加一段d=0.11λg=7.45 mm 的微带延长线,如图4(c)所示。此时微带线上的电场幅值均匀分布,大小一致(见图4(d))。这一结果证明了通过单支节短截线匹配网络,实现了微带线与负载之间的阻抗匹配,此时微带线上不存在反射波。

图4 微带线结构与电场分布
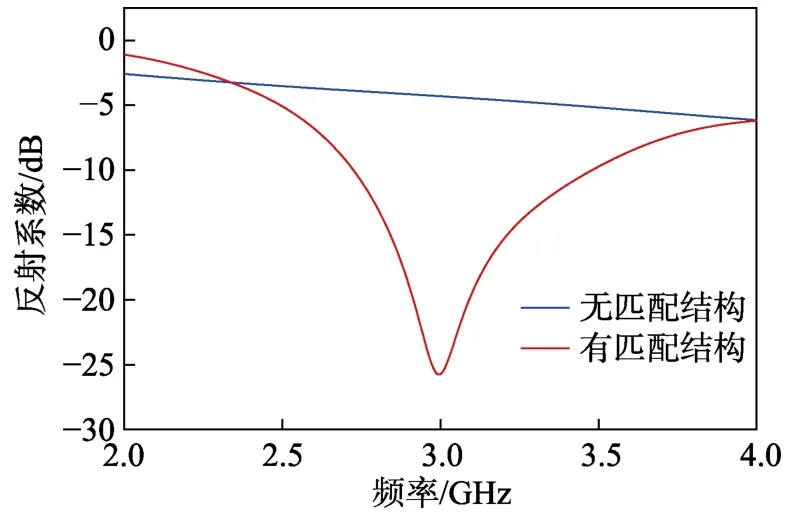
图5 微带线反射系数
同时,经过CST 微波工作室的仿真,可以得到这两种结构的反射系数,如图5 所示。通过对比仿真曲线可以看出,无匹配结构的反射系数较大。而单支节匹配网络使微带线与负载之间具有良好的匹配,反射系数在3 GHz 得到明显改善。仿真结果与理论分析较为吻合,验证了单支节匹配网络的设计。
本节通过电磁仿真软件,构建微带线模型,对匹配网络进行实验验证,所得电场幅值分布与反射系数都证实了我们的阻抗匹配网络设计可靠有效。该实验案例有助于学生理解传输线阻抗匹配的概念和设计方法,同时也提高探索复杂工程问题的能力。
4 结语
为了增强学生对传输线阻抗匹配的理解,本文提出了微带线阻抗匹配网络设计教学实验。实验的实施步骤包括阻抗反射分析、匹配网络设计、微带线阻抗匹配结构建模、CST 电磁仿真实验验证。实验结果直观展示了阻抗匹配的效果,使学生从理论推导与物理现象两个方面加深了对阻抗匹配概念和理论的理解,并激发学生的学习兴趣和科研思维能力。

