基于BRT智能公交调度系统研究
杨 丹,王治东,陈 晨
(西南科技大学城市学院,四川 绵阳 621000)
1 智慧交通概念
随着网络时代的快速更新以及5G时代的到来,中国居民传统生活模式逐渐被智慧化,“慧医疗、慧农业”等如雨后春笋般迅速崛起,交通作为人们“衣食住行”的重要一环,因此“智慧交通”的快速发展必不可少。“智慧交通”是指交通运输、网络技术相互融合的现代化产物,是目前解决城市交通拥堵、交通安全、节能减排有效措施。以此建立起一种在实用范围广、作用发挥强的实用、智能、高效的交通管理运输系统,目前我国智能化交通建设主要涵盖运输服务、公共交通服务、城市交通指挥及港行服务四个方面。
2 BRT快速公交
快速公交系统是顺应时代所需的一种新型的公共客运系统,其建设投资成本比轨道交通低,而运营效果却于轨道交通相似。充分结合了现代化公交技术和智能运输和运营管理技术,开创了公交站台售票的新理念,实现公共交通式运营服务,达到轨道服务水准的一种独特的城市客运系统。
BRT快速公交系统目前在长沙、郑州等将近20多个城市推出和使用,快速公交的诞生大幅度缓解了大城市的交通压力,缓解了公共交通乘车拥堵和时间等待的现象,与此同时这种交通形式涉及到城市发展、公共设施、市民出行心理、城市道路设置等诸多因素,在快速公交设计规划时充分考虑相应因素,以期建立一个让市民更加满意的新型公共交通系统是BRT快速公交系统服务设计所努力的方向和动力来源。
3 研究现状
目前,我国大部分城市都采用传统的公交调度模式,通过以往客流经验进行制定发展频率,并且在车辆发出后不在对其管控,该种方式虽然操作简单,但其实际效果并不好,每当晚高峰来临时,部分公交车站总会存在停车拥堵,甚至影响了其它路线车辆的正常行驶,出现同一线路公交同时停靠在一个站台的现象,同时由于调度中心无法及时指导站台乘客的乘车需求,导致经常出现乘客等车时间过长或车辆满载率过低等情况发生,从而导致公交服务水平底下,客流日益减少。
本文主要针对现有的城市公交运行调度系统,着力解决调度系统与乘客乘车需求不平衡的问题以及提高运营系统的抗干扰性能,特别是晚高峰,繁华地段的公交车站会出现大量公交车排队停靠的现象,甚至有些公交车虽无乘客在该站台上下车,但只是按运营制度停靠。这样的拥堵对资源和时间都存在严重的浪费,极大地延长了公交的运行时间,给乘客的出行带来了极大的不便。造成这一现象的主要原因是城市道路拥堵扰乱了公交车的正常运行秩序,公交的拥堵又反向加重道路拥堵,如此恶性循环,导致整个道路运行效率降低。
4 研究方法
4.1 站台操作
在BRT站台,乘客可通过站台售票机输入目的地进行路线查询或者直接通过已定线路选择站点,此时售票机会根据乘客的相应操作做出路线推选,确认操做完成后进行付款方式选定购票,支付成功后此时系统会将乘客的乘车数据传送至指挥中心后台,进行下一步处理。
4.2 调度中心处理
调度中心作为车辆和乘客之间信息传递的纽带,主要负责将乘客的乘车信息优化处理后通过后台终端设备将乘车信息传送至车载设备,车载设备接收道调度中心传来的信号后,通过相应处理简化,以语音或信号灯的方式提醒司机,司机可根据车载设备提前预知下站是否有乘客上下车,若无可不进站直接开往下一站。
4.3 运行流程
(1)只上不下
乘客A在站台X发出前往站台Y的乘车需求,此时调度中心向离站台X最近距离(≧50 m)的公交车传递乘车需求,此时司机做好停靠站台X准备。若公交车在离站台X很近(≦50 m)时收到乘客乘车需求,同时该车在进入缓冲距离前没有接到停靠站台X的需求时,该公交车不再受理本乘客交由下一辆公交车受理。
(2)有上有下
若乘客A乘坐1路公交且目的地为下一站台X,为优先满足下车乘客需求,无论下一站台X是否有乘客上车,公交车都必须停靠站台X。同时为满足“有车必载”的运营理念,此时公交车无论离站台X多远,只要乘客B在该公交车到达站台X之前发出乘车需求,该公交车都必须受理本乘客。
(3)站台重复
在城市众多公交线路中,有相当部分线路存在站点重合,及乘客出行存在多种路线选择时,此时为了尽可能的减少公交车进站停靠造成拥挤和节约车辆运行时间,此时调度中心就需根据实际情况进行车辆安排,其原则如下:
若两车均距离乘客起始站较近时,此时在该站台有下车需求的车辆优先;若另一路线上的公交车距离乘客起始站较远,此时由距离较近的车辆优先。
5 流程量化
5.1 模型分析
最优路线推荐主要针对乘客需要中转情况,此时分两种形式,一种是乘客知道终点站台,另一种为乘客不知道终点站台只知道目的地。对于第二种情况,站台一体机需通过对目的地周围500 m范围内的所有公交进行统计,将范围内所有的站台都默认为乘客的终点站台。当终点站台确定后,此时系统通过求解最优数学模型将运行时间最小值所在路径作为最优乘车方案推荐给乘客。
5.2 模型建立基础
日常乘车中,乘客总需要一个路径最短、时间最少、少转车的乘车方案。但在现实生活中这同时实现三个最优几乎是不可能事件。通过建立最优数学模型、采用集合法将路径、时间进行量化,然后通过建立时间最优模型求解最优值。本文通过差分迭代方程的计算,这种方法与近似积分的数学模型等价,在一定范围内可与实际结果相似。建立数学模型主要需解决以下问题:
——如何确立乘车路线;
——怎样确定乘车路线最优;
5.3 符号约定及说明
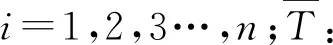
5.4 模型的建立及求解
(1)乘车路线确定
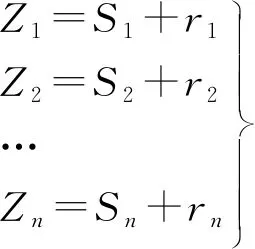
Zmin=min{Z1、Z2、…、Zi}且Zmin=Y*
当:
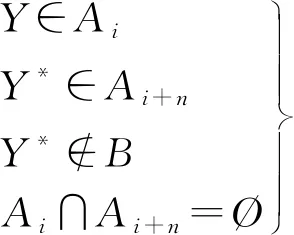
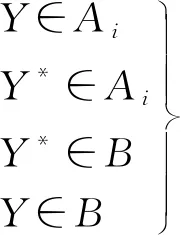
①乘客起始站与目的地无可乘车路线;
α、β,即相应值不存在
②乘客起始站与目的地有乘车路线,但需要转车;
Zmin={min(S1、S2、…、Si)+min(Z1、Z2、…、Zi)}
③乘客起始站与目的地有乘车路线,且不需要转车;
Zmin=min{S1、S2、…、Si}
此时所有可乘路线都应满足以下关系式:
B∈Ai∪Ai+n
(2)确定乘车路线最优
英国TRRL认为道路的通行速度主要与道路流量和行车道宽度有关,所研发的适用于城市中心区道路的交通阻抗模型为:
Vq=49.9-0.163(q+430)/(W-R)
16 Vq=67.6-0.123(q+1 000)/(W-R) 32 式中:Vq:路段交通量为q时的行车速度,km/h,此处取第一个模型;W:行车道宽度,单位m;R:行车道宽度的减少值,单位m。 美国联邦公路局的路阻函数模型在路阻函数的研究中,其研究路阻函数模型BPR函数是最有代表意义的一个研究成果,此模型在交通规划界应用相对广泛,具有一定的权威性,其数学表达式为。 Tq=T0[1+α(q/c)β] 式中:Tq:当流量为q时路段上的行程时间;T0:零流量时车辆在路段上的行驶时间;c:路段的实际通行能力;α、β:模型参数,常取α=0.15,β=4.0。 通过调查发现,在城市众多公交线路中,由于道路实际情况以及乘客上下车的突发情况往往会对实验结果产生一定影响,即使公交车行驶速度相同的条件下,距离最近的道路行驶时间不一定最短,理论运行最优时间路线不一定为最优路线,为了提高模型的抗干扰性,减小实验结果误差,通过建立多目标函数,对不同函数加以权重约束,通过求解选定最优乘车路线,其函数模型如下 此时系统将满足条件的可乘路线作为最优路线推荐给乘客。 模型借助了传统多目标函数规划理念,通过集合知识将各线路站台量化,一个站台对应一个子集, 最后采用差值比较法求出实际最小行车路线,同时为了提高行车路线的优化程度,引入国外相对成熟的路阻模型作为理论依据,两者相互制约完善,与差值比较法得出的结果共同构成二元多目标函数,同时对其影响权重做出调整,最终建立多目标函数规划模型,得出满足条件的最优路线。 本模型的建立可为BRT快速公交调度系统优化完善提供一定理论依据,解决了公交车辆“盲目进站”的问题,既在一定程度上缓解了公交车排队进站的拥挤场面,也缩短可乘客的乘坐时间,更好的平衡了需求、资源、时间三者间的关系,具有惠民互利的作用,一定程度上完善了“智慧交通”的发展缺陷,为我国交通行业飞速发展做出细微贡献。 公共交通作为各大城市交通出行的重要组成部分,在人们日常出行中占有举足轻重的地位,公交系统的快速发展不仅会促进居民外出消费,而且也可作为城市综合实力展现的名片。在未来,中国的交通必将朝着智能化、高效化、绿色环保的多元化方向发展,通过不懈努力,最终站在世界领域前端,让我国人民充分感受“智慧生活”所带来的舒适感。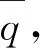
5.5 模型评价与分析
6 结 论

