新型剑杆织机引纬机构的反求建模与运动学仿真
喻陈楠, 贾江鸣,2, 陈之威, 陈建能,2, 陈加友, 陆文韬
(1. 浙江理工大学 机械与自动控制学院, 浙江 杭州 310018; 2. 浙江理工大学 浙江省种植装备技术重点实验室, 浙江 杭州 310018; 3. 福建佳友茶叶机械智能科技股份有限公司, 福建 泉州 362400)
引纬机构是剑杆织机的重要组成部分,其将输入端即主轴的匀速回转转化成输出端即剑头的往复直线运动,从而引导纬纱进入梭口,引纬机构对于织机的性能产生重要影响[1]。
剑杆织机的引纬方式有共轭凸轮引纬、变导程螺旋引纬、差动轮系连杆机构传动引纬、空间四杆机构引纬等[2]。共轭凸轮引纬机构是应用最广的机构,其采用分离式筘座,有利于提高引纬速度,但是共轭凸轮结构复杂,加工要求高,其设计加工的好坏对整机性能产生较大影响,若制造精度不够会导致磨损严重,振动冲击加剧,性能降低[3-4]。变导程螺旋引纬机构的传动部分可简化成曲柄滑块传动机构,其结构简单紧凑,但是变导程螺杆加工要求高,而且传动效率低,对于不同的筘副,其通用性较差[5]。差动轮系连杆机构传动的引纬机构虽然能够实现“接力”引纬,但是该机构传动链较长,而且其剑头加速度不如前2个机构理想。空间四杆机构引纬能使剑杆在夹取和交接纬纱时具有较小的速度,但是其设计灵活性较差[6-7]。
本文基于前期研究成果[8-10],提出了一种新型偏心圆-非圆齿轮行星轮系引纬机构,相比于上述机构其具有设计灵活、结构紧凑、传动链短、加工难度小等优点。建立了由理想引纬运动特性反求机构参数的数学模型。基于MatLab编写了该引纬机构反求设计与仿真分析软件,对该机构进行参数优化和运动模拟,得到较优的机构参数。最后对该引纬机构进行三维建模和运动学仿真。
1 新型引纬机构简介
图1示出新型偏心圆-非圆齿轮行星轮系引纬机构简图。图中区域Ⅰ为偏心圆-非圆齿轮行星轮系传动部分,区域Ⅱ为放大轮系传动部分。该机构传动原理为:织机主轴驱动行星架转动,从而带动位于行星架两侧的行星轴周向转动;与主动偏心圆太阳轮共轭的从动非圆行星轮和主动非圆行星轮均固连在行星轴上,且主动偏心圆太阳轮保持固定;通过主动偏心圆太阳轮和与其共轭的2个从动非圆行星轮啮合以及2个主动非圆行星轮和从动非圆太阳轮啮合,可将区域Ⅰ内的输入端即织机主轴的匀速回转转变为输出端即从动非圆太阳轮轴的非匀速往复转动。在区域Ⅱ内,大圆柱齿轮与小圆柱齿轮,大圆锥齿轮与小圆锥齿轮组成行程放大机构,将从动非圆太阳轮的回摆角度通过剑轮进行放大。
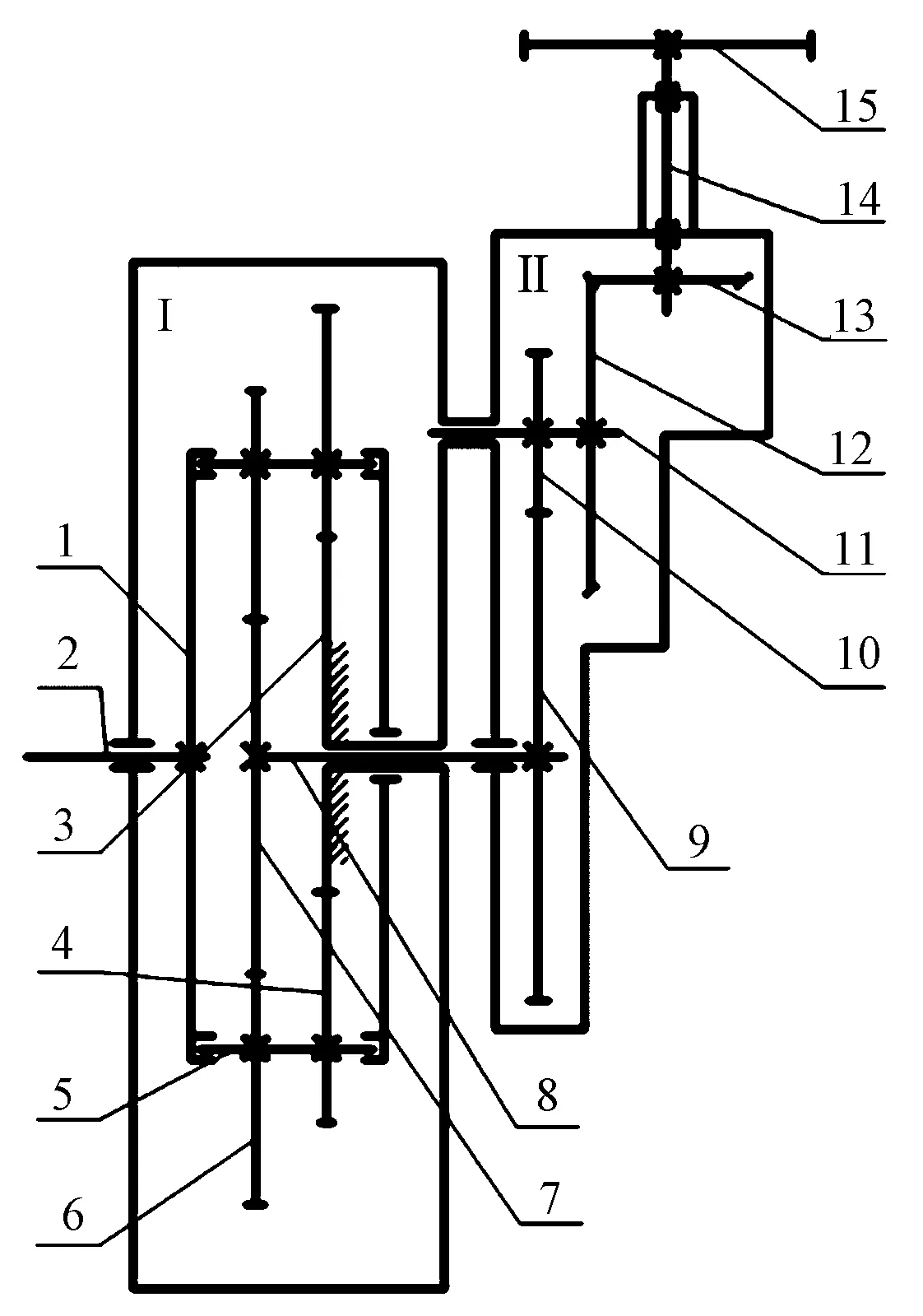
1—行星架; 2—织机主轴; 3—主动偏心圆太阳轮; 4—从动共轭非圆行星轮; 5—行星轴; 6—主动非圆行星轮; 7—从动非圆太阳轮; 8—从动非圆太阳轮轴; 9—大圆柱齿轮; 10—小圆柱齿轮; 11—小圆柱齿轮轴; 12—大圆锥齿轮; 13—小圆锥齿轮; 14—小圆锥齿轮轴; 15—剑轮。
从动非圆太阳轮轴与织机主轴共线,主动偏心圆太阳轮跟从动共轭非圆行星轮的中心距等于主动非圆行星轮跟从动非圆太阳轮的中心距。该偏心圆-非圆齿轮行星轮系引纬机构传动链更短,结构更紧凑,且可通过调整非圆齿轮的节曲线来实现不同的引纬运动规律,具有更好的设计灵活性。
2 剑杆引纬规律
2.1 理想的剑杆运动规律
剑头运动规律应当符合引纬工艺要求,以1个周期为例,其具体要求[11]如下:1)位移条件:最大位移发生在主轴旋转180°时,此时剑头位于梭口中央,最小位移发生在主轴位于初始位置或者转过360°时,此时剑头位于梭口两侧的指定位置。2)速度条件:进剑时,剑杆由静止开始运动,当速度达到最大后开始减小,当主轴旋转180°即当剑头位于梭口中央时,速度减小为零;退剑时,剑杆同样从静止开始运动,速度达到最大后开始减小,当主轴旋转360°即当剑头位于梭口两侧时,速度为零。3)加速度条件:剑杆由静止启动时,加速度不宜过大,加速度峰值应尽可能小。
2.2 剑杆运动规律的设定
保持剑头位移不变,修正梯形加速度运动规律与正弦函数加速度运动规律相比,加速度峰值减少了45%,速度峰值减少了4%[12-13]。本文以3次Hermite插值多项式为过渡段,构造加速度运动方程[14],再推导出速度和位移方程。

(1)

设剑头的单边总动程为1.4 m,根据工艺参数要求取φ1=30°,φ2=75°,φ3=120°,相应的引纬运动规律曲线如图2所示。
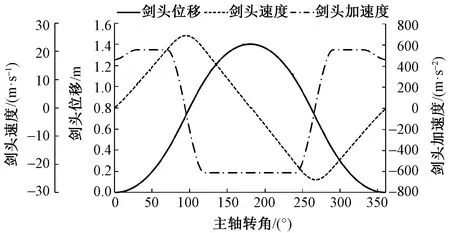
图2 引纬运动规律
3 引纬机构建模及软件的开发
该引纬机构区域Ⅰ中第1级采用偏心圆-共轭非圆齿轮传动,第2级采用一对非圆齿轮传动,以图2所示引纬运动规律为条件可反求非圆齿轮节曲线。
3.1 第1级偏心圆齿轮行星轮系建模

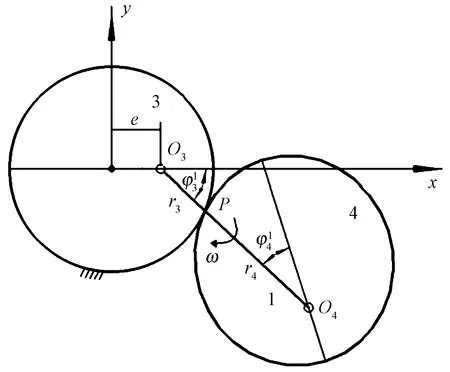
图3 第1级偏心圆-共轭非圆传动简图
给定主动偏心圆齿轮3的节曲线是偏心圆,相对于其回转中心,它是一个非圆齿轮,其节曲线方程[15]为
(2)
式中:r3为主动偏心圆齿轮3的向径,mm;R为偏心圆半径,mm;ε为偏心率,ε=e/R;e为偏心距,mm。r3以2π为1个周期,即n3=1。设要求在从动轮4的1个周期中,r4的变化周期数为n4,则齿轮4的节曲线封闭条件为
(3)
由式(3)可求得中心距a(mm)。因此从动非圆行星轮4的节曲线方程为
(4)
式中:r4为从动共轭非圆齿轮4的向径,mm。第1级齿轮副的传动比为
(5)

3.2 第2级非圆齿轮行星轮系反求建模
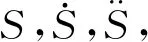
φ7=s/(rif)
(6)
(7)
(8)
(9)
式中:r为剑轮半径,mm;if为放大轮系的总传动比;z9、z10、z12、z13为齿轮9、10、12、13的齿数。
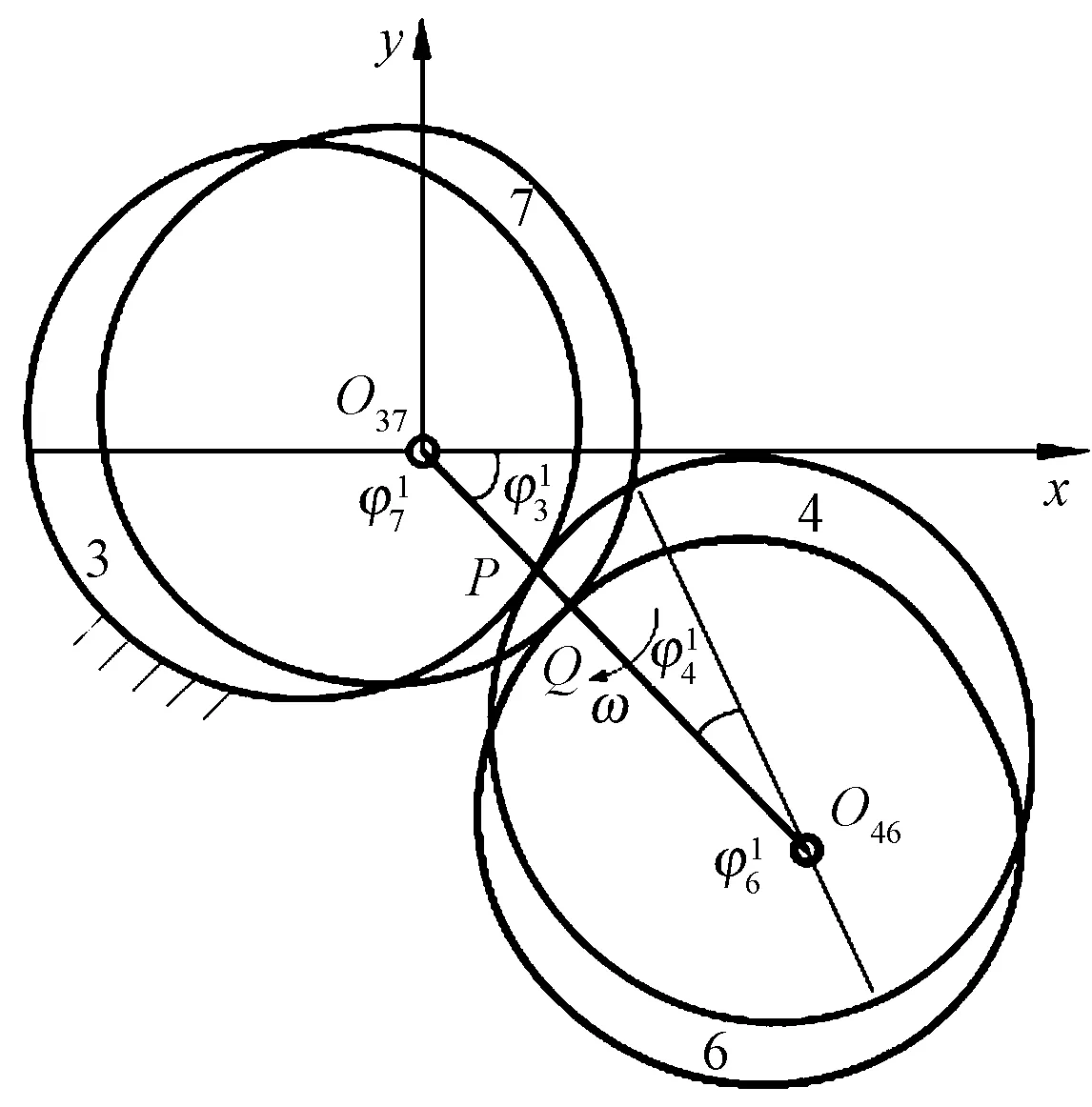
图4 第2级非圆齿轮行星轮系传动简图
从动非圆太阳轮7与行星架1传动比为i71=dφ7/dφ1,由于φ3=0,有:
(10)

(11)
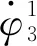
设此时主动非圆行星轮6和从动非圆太阳轮7啮合时的向径为r6和r7,则:
(12)
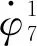
行星轴5与织机主轴2之间的距离为
r3+r4=r6+r7=a
(13)
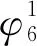
(14)
(15)
3.3 引纬机构反求设计与仿真软件的开发
基于上述引纬机构的运动学模型,利用MatLab编写了该引纬机构的反求设计与仿真软件。该软件主要用于偏心圆-非圆齿轮行星轮系引纬机构的反求设计和运动学仿真分析,能够根据机构参数的变化实时地计算输出参数,显示非圆齿轮行星轮系的运动传递方式,并模拟机构运动,最终可将所有机构输入参数和输出数据进行数据保存。用户可根据界面的显示结果结合实际工艺要求判断剑头运动学曲线是否合理、构件之间是否干涉以及非圆齿轮的节曲线是否满足工作需求等;用户还可根据界面显示结果,调整所输入的机构参数和工艺参数,进一步优化非圆齿轮节曲线。图5示出该软件的结构图。
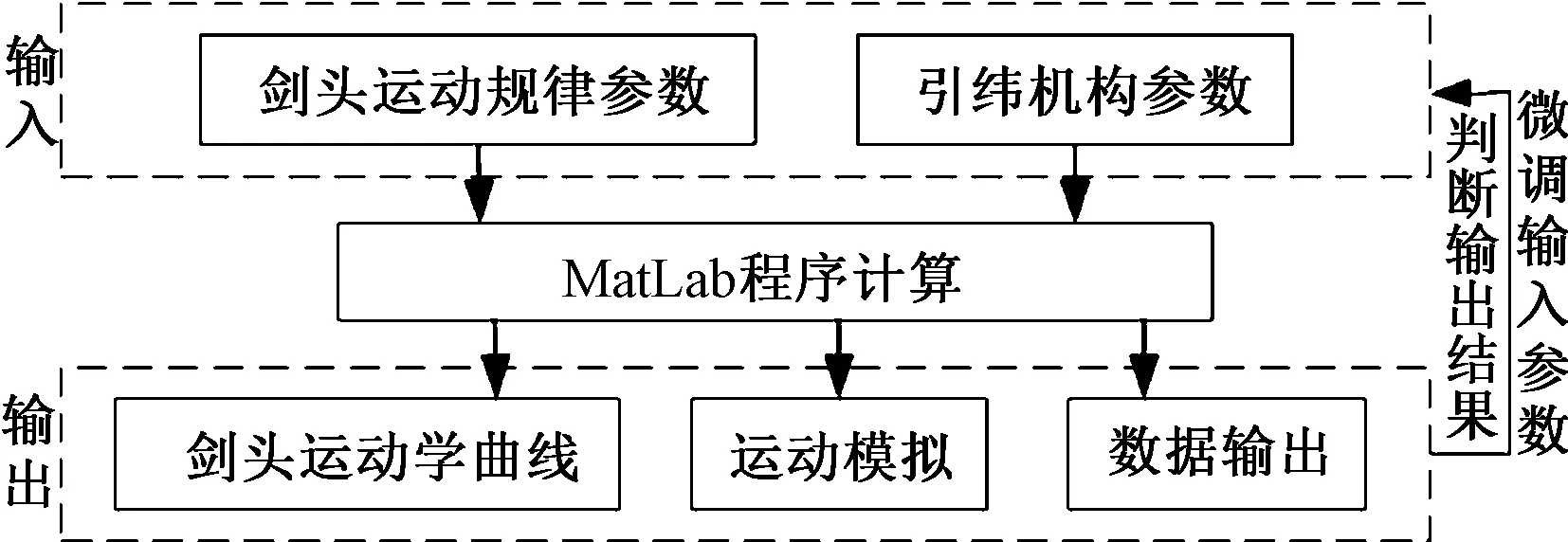
图5 软件结构示意图
软件结构图中所输入的剑头运动规律参数包括:主轴转速n,正向加速度峰值h,比例系数C1,3个角度参数(分别对应2.2节中的φ1、φ2、φ3);引纬机构参数包括:偏心圆半径R,偏心距e,接纬提前角δ,剑轮半径r,放大轮系中齿轮9,10,12,13的齿数及模数z9、z10、z12、z13、m9,10、m12,13,交接冲程J。经MatLab程序计算,可输出剑头位移、速度和加速度曲线,对引纬机构进行运动仿真,并且可输出从动非圆太阳轮7的摆角、放大轮系传动比、单边总行程和接纬剑头位移等重要参数,最后根据输出结果微调输入参数,进一步优化机构性能。
图6示出该引纬机构反求设计与仿真软件整体界面。界面上显示的是当织机主轴转动180°时,引纬机构的各项输入参数、剑头运动规律曲线、机构瞬时运动状态、送纬剑和接纬剑的运动状态以及重要输出数据等。该软件的主要功能如下:图6中的区域1为参数输入区,包括剑头运动规律参数输入和引纬机构参数输入。区域2为机构简图显示区和机构运动仿真区,由区域2可知,当织机主轴转动180°时,行星架处于水平位置,并且两剑头运动到了梭口中央,进行纬纱交接,在区域2中也可进行运动干涉检验。区域3为控制键区,点击“机构示意图”可在区域2中查看如图1所示的机构简图;点击“参数计算”可根据区域1中的输入进行参数计算并将部分重要参数在区域5中输出;点击“初始位置”可在区域2内显示初始时刻的引纬机构示意图;在显示机构初始位置后点击“运动仿真”可在区域2内进行机构运动模拟,并在区域4内绘出剑头的运动学曲线,每条曲线上都有1个运动的圆点,代表当前剑头的加速度、速度和位移数值;点击“步进”/“歩退”可使引纬机构的主轴进行步进/歩退的运动,步长为1°;点击“暂停”可使区域2内的运动模拟暂停;点击“保存数据”,该软件将自动弹出另存为界面,进而保存所有的输入和输出数据;点击“退出”,则退出程序。区域4为剑头运动学曲线,由区域4可知当织机主轴转动180°(即圆点处)时,两剑头从梭口两侧运动到了梭口中央,此时达到了最大位移,速度降为零,有利于降低交接时纬纱张力,保证两剑头交接无误。区域5为重要参数输出区。
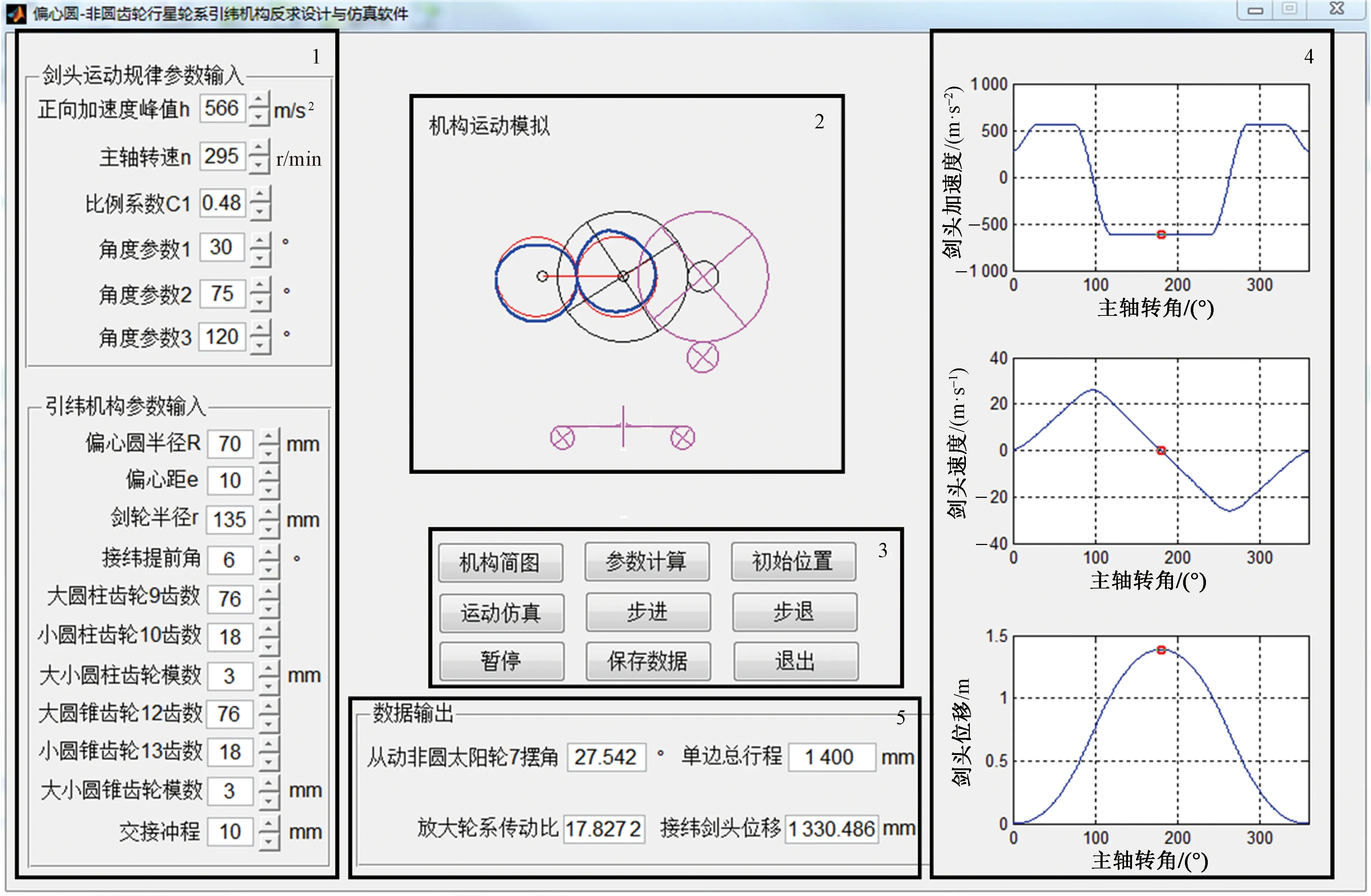
图6 软件界面
3.4 引纬机构反求设计与仿真软件的应用
3.3节开发的偏心圆-非圆齿轮行星轮系引纬机构反求设计与仿真软件,不仅可进行机构的运动模拟,还可离散点坐标的形式保存非圆齿轮节曲线。本文利用该软件分析2个关键参数(偏心圆齿轮的偏心距和放大轮系的总传动比)对主动非圆行星轮6和从动非圆太阳轮7的节曲线的影响。
3.4.1 偏心距对非圆齿轮节曲线的影响
图7示出当偏心圆齿轮(图中1,2,3)的偏心距分别为e1=10 mm,e2=20 mm,e3=30 mm时所对应的非圆齿轮6和7的节曲线。由图7可知,偏心距越小,非圆齿轮6和7的节曲线形状越趋于圆形,且中心距越小,越利于稳定传动。所以第一级主动偏心圆太阳轮3的偏心距取e=10 mm。
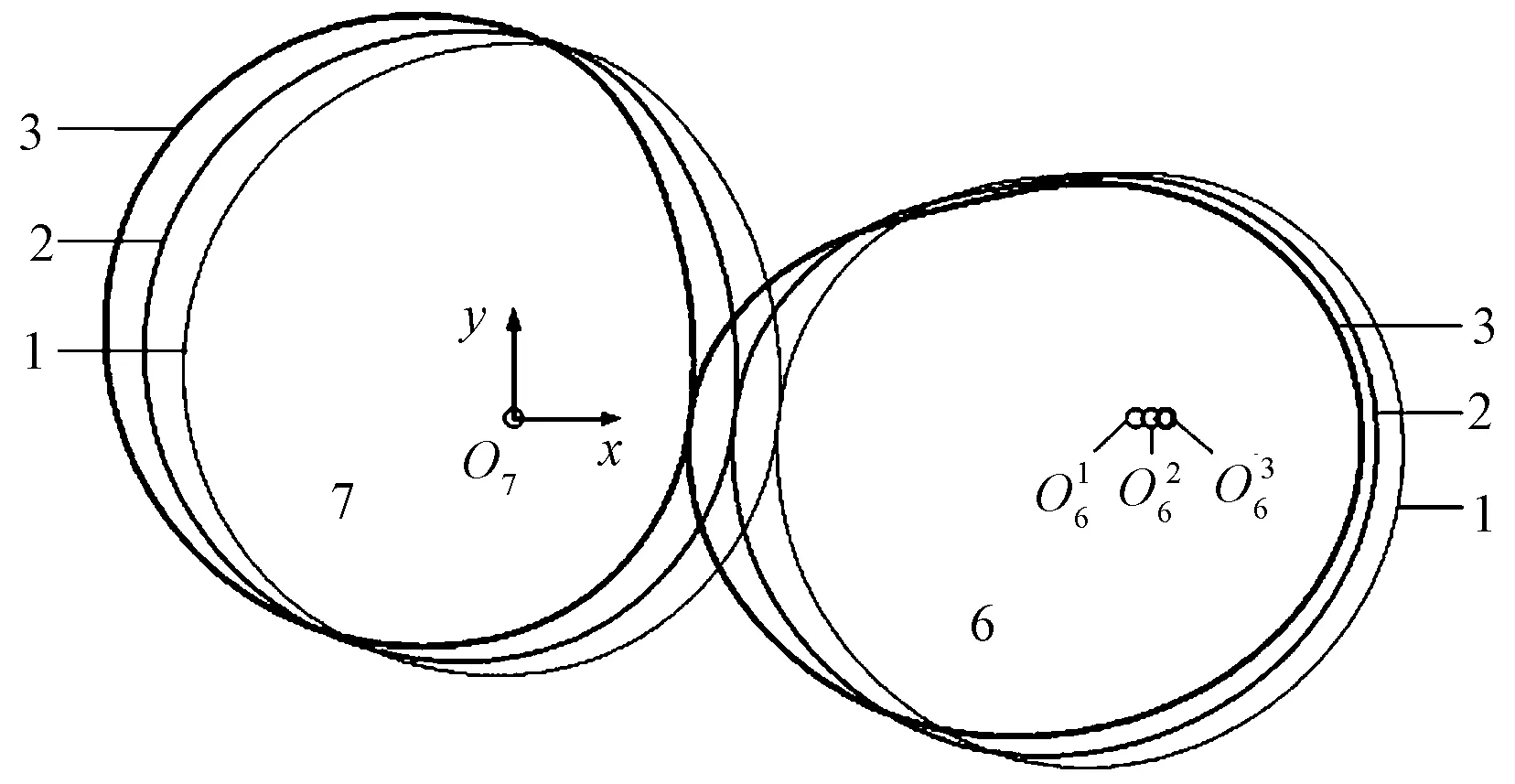
注:分别为不同偏心距e1、e2、e3下非圆齿轮6的回转中心。
3.4.2 总传动比对非圆齿轮节曲线的影响
图8示出当放大轮系(图中1,2,3)的总传动比分别为if1=13.811 ,if2=17.827 ,if3=26.471 时所对应的非圆齿轮6和7的节曲线。由图可知,放大轮系的总传动比越小,齿轮7的节曲线上凸角越尖,且齿轮6的节曲线存在内凹趋势,因此行程放大轮系的总传动比不能过小。同时总传动比也不宜过大,因为总传动比过大可能会导致机构尺寸过大或者小齿轮10和13的齿数过少从而在加工过程中发生根切,此处取行程放大轮系的总传动比if=17.827 。
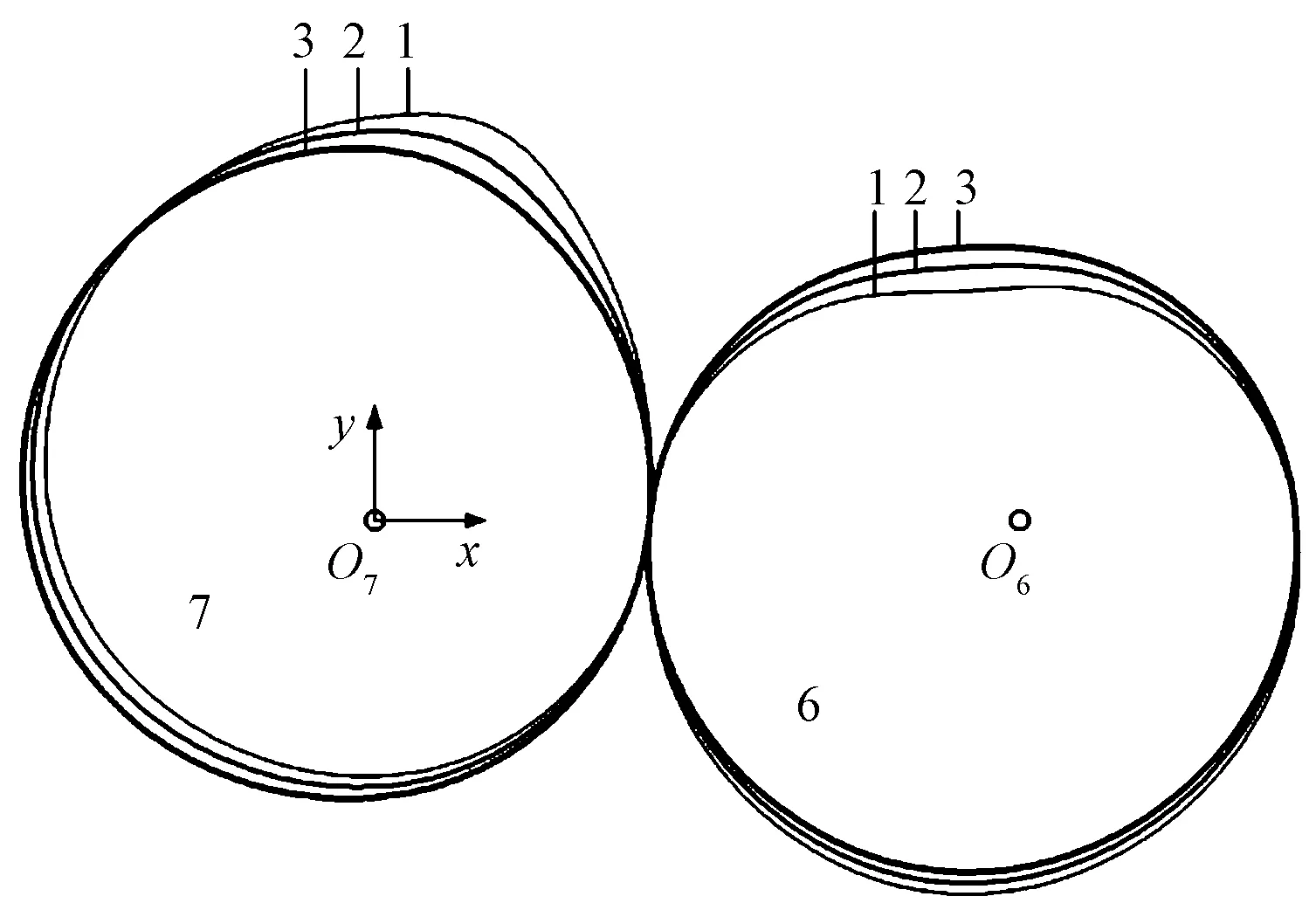
图8 不同放大轮系总传动比下的非圆齿轮节曲线对比
3.5 引纬机构参数优选
利用偏心圆-非圆齿轮行星轮系引纬机构反求设计与仿真软件,结合偏心圆齿轮偏心距和放大轮系总传动比对非圆齿轮6和7的节曲线的影响,获得了一组较优的机构参数:偏心圆齿轮的半径R=70 mm,偏心距e=10 mm,剑轮半径r=135 mm,行程放大轮系的总传动比if=17.827 ,z9=76,z10=18,m9=m10=3,z12=76,z13=18,m12=m13=3。
4 引纬机构三维建模及仿真分析
基于已确定的引纬机构参数,本文对该引纬机构进行三维建模,利用ADAMS进行仿真分析,进一步验证该引纬机构的可行性。
4.1 引纬机构的三维建模
第1级和第2级非圆齿轮的三维模型如图9所示。

图9 两级非圆齿轮的三维模型
由于引纬机构中从动非圆太阳轮与剑轮二者的运动规律呈线性关系,即存在放大轮系传动比的倍数关系,因此本节只对引纬机构的偏心圆-非圆齿轮行星轮系传动部分(即图1中的区域Ⅰ)进行建模,行星轮系传动部分的三维图如图10所示。
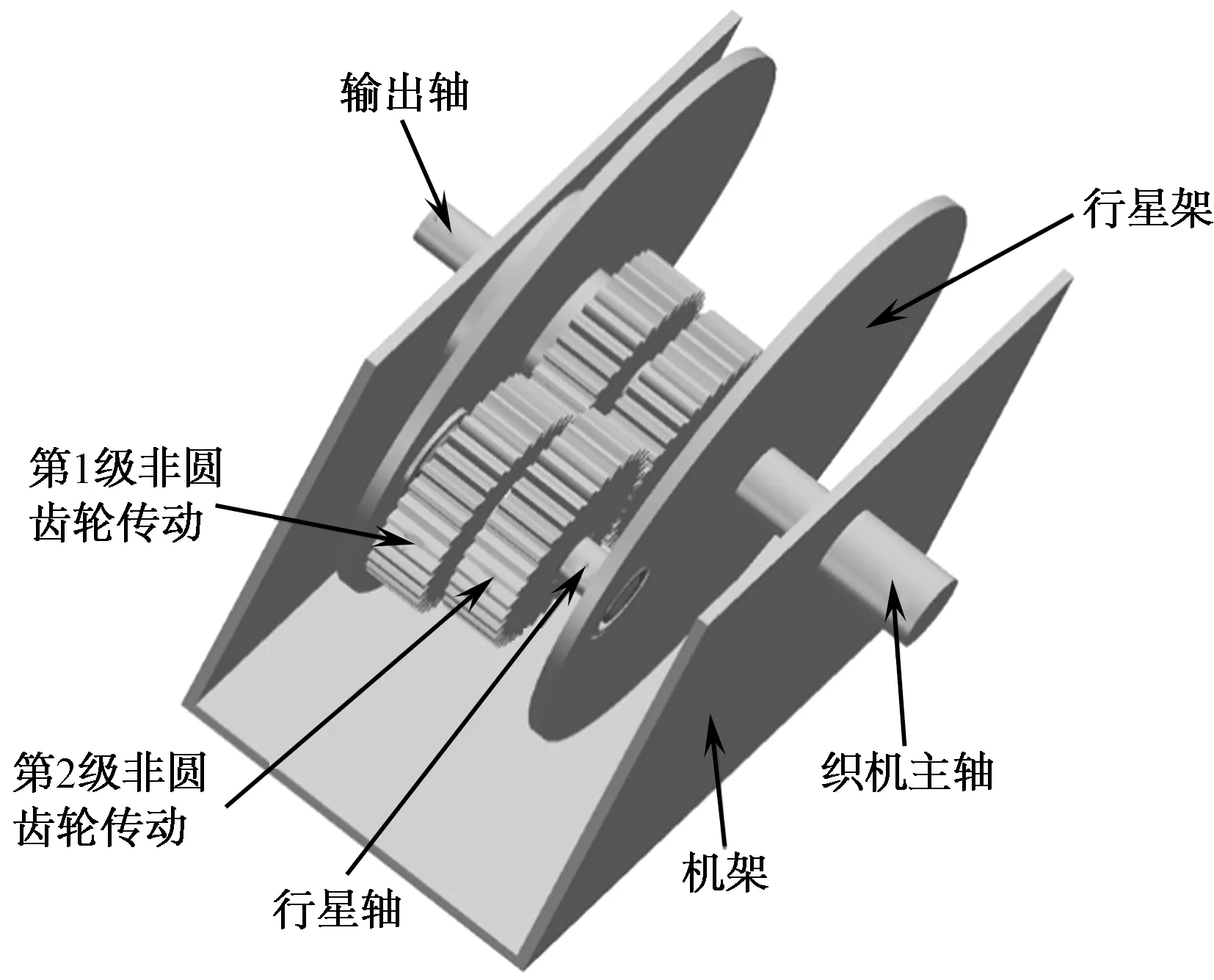
图10 偏心圆-非圆齿轮行星轮系传动部分三维图
4.2 引纬机构的虚拟样机运动学仿真
将模型文件导入到ADAMS软件中进行仿真,仿真得到的运动学曲线为图10中输出轴的角位移、角速度和角加速度曲线,需要将其转化为剑头的位移、速度和加速度曲线,以便对比分析仿真结果。表1示出引纬剑头的位移、速度和加速度的仿真和理论峰值。图11示出引纬剑头的位移、速度和加速度的仿真和理论曲线。
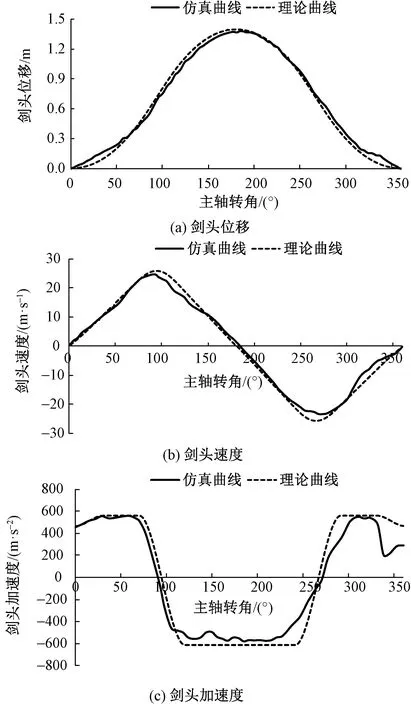
图11 引纬剑头的理论与仿真运动规律对比
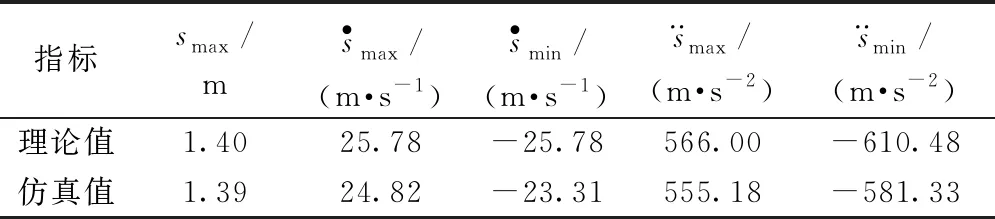
表1 剑头运动规律的理论峰值与仿真峰值对比

5 结 论
1) 本文提出新型偏心圆-非圆齿轮行星轮系引纬机构,分析了引纬剑头的运动特性,选取了一种理想的剑头运动规律曲线,并建立了由理想引纬运动特性反求机构参数的数学模型,并反求得到了非圆齿轮的节曲线方程。
2) 根据引纬机构的数学模型,基于MatLab编写了该引纬机构的反求设计与仿真软件。该软件可输出非圆齿轮节曲线的离散点数据,可进行机构的参数优化和运动模拟,也可用来分析关键参数对第2级非圆齿轮节曲线的影响。
3) 根据已优化的机构参数,建立了该引纬机构的三维模型,并利用ADAMS进行了仿真试验。结果显示仿真和理论的剑头运动学曲线基本一致,验证了对该引纬机构建模和分析的正确性,也表明了该引纬机构可以满足工作要求。

