舰艇对空自防御系统仿真试验目标模拟技术研究∗
(91336部队 秦皇岛 066326)
1 引言
现代反舰导弹在飞行高度、速度和弹道的控制上越来越灵活,形成的协同攻击态势越来越复杂多变,这对水面舰艇的生存带来严峻挑战,因此对空自防御作战能力成为水面舰船综合作战能力的重要组成部分,是舰艇做好自身防护的关键。通常舰艇对空自防御系统主要由预警探测设备,作战指控控制系统,导弹、火炮及电子战软硬抗击武器系统组成。对空自防御的一般过程是,预警探测设备将感知的威胁目标信息送到指控系统,指控系统进行目标航迹融合、威胁判断、火力分配处理后形成目指信息,软硬武器根据目指信息进行软硬武器协同抗击发射,这是一个比较典型的OODA作战过程。
要检验舰艇对空自防御的能力,采用靶机模拟真实导弹的攻击,舰艇组织软硬武器进行自防御抗击,这样是最真实、最直接、最有效的,但是存在样本量有限、效费比不高的问题,国内外研究单位都将仿真手段作为研究对空自防御效能分析的有效补充。陈炜、王小飞研究了一种舰载指控系统情报处理性能仿真测试评估方法,在实验室条件下,通过模拟各类情报信息输入指控系统完成测试[1]。朱忍胜、谢红卫等研究了一种水面舰船对空自防御作战能力计算模型,重点分析了目指时间对拦截次数的影响[2]。徐大江研究了基于着色Petri网的舰艇自防御建模仿真,建立了舰艇对空自防御作战任务划分层次模型、信息流动模型和运行组织模型,对舰艇自防御过程进行了仿真分析[3]。吴亮分析研究了舰艇对空自防御系统效能评估与联合试验环境的构建方法[4]。石剑琛研究了美国海军基于仿真的舰艇自防御测试,分析了美国以分布式、互联协同仿真为核心,构建一个能支持系统现场测试毁伤概率的仿真环境[5]。上述研究,对舰艇对空自防御的仿真测试和分析评估都做出了非常重要的贡献,本文将重点研究在实装条件下的在线仿真测试与评估,建立威胁目标的运动模型,生成在线仿真驱动数据,实现对空自防御系统的仿真测试评估。
2 基于数据驱动的在线仿真方法
舰艇实装条件下的仿真测试,具有装备系统构建齐全、信息流转反馈完整的特点,测试对象都是实装本身,因此测试的结果就比较可信,但是对测试环境和测试手段的构建就不同于实验室环境,需要与实装系统具有准确的信息匹配和灵活便捷的测试方式,因此在线仿真测试的要求是准确、高效、便捷。
本文提出的基于数据驱动的在线仿真方法[6~7],将目标探测过程采用建模仿真的方法实现,将导弹威胁态势按照警戒探测设备的时空匹配、探测时序和工作状态要求解算成数据报文,在时钟对准的条件下依据时序逻辑推送到舰艇作战网上;舰艇作战指挥系统接收到信息报文后,进行目标融合、威胁判断、火力分配形成作战方案,并对软硬武器下达目指信息;软硬武器根据目指信息进行射击诸元解算、武器控制和状态反馈,实际不发射武器,状态反馈采用模拟信息;数据录取设备录取威胁目标信息、目指信息和各种状态反馈信息,用于进行系统分析评估。仿真测试过程如图1所示。
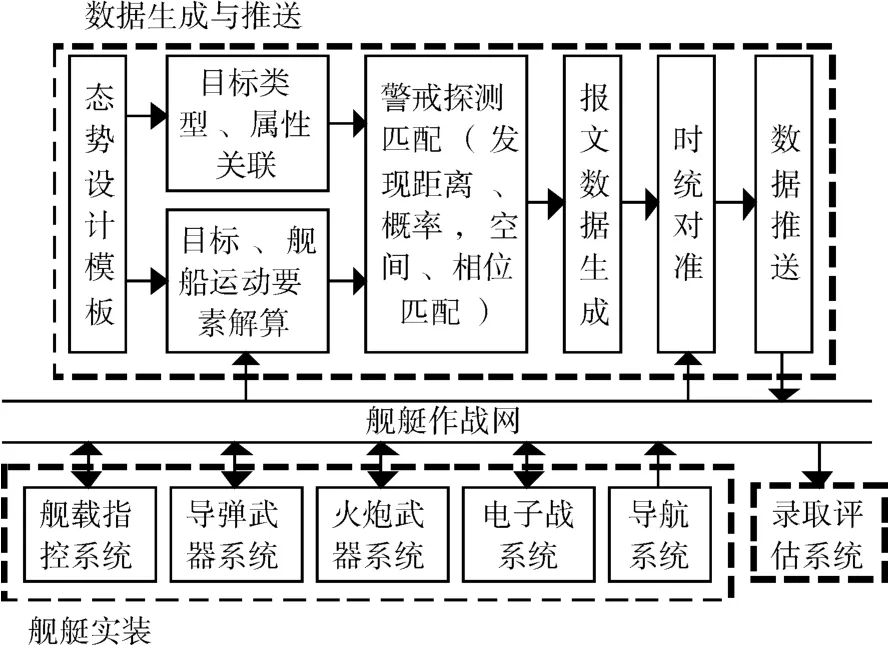
图1 数据驱动在线仿真过程示意图
图1中的数据与推送部分是本文的核心工作。态势设计模板是基于Excel的参数化表格文档,将态势设计的目标位置、运动、弹道等要素,目标类型、属性、威胁等级等要素,也就是将警戒探测报文中的变量因素全部在Excel表格中列出。采用Matlab软件读取Excel态势文件,进行目标与舰船的相对运动解算,关联目标属性参数,然后进行坐标变换和探测能力匹配,生成试验态势的时序报文数据。时统对准和数据推送软件,读取舰艇作战网上的时统报文,修正态势数据报文的时戳,然后按照时序将各警戒探测设备的报文数据推送给本指系统。
3 目标模拟的算法基础
通常描述一枚导弹来袭态势会用到距离、航向、速度、航捷和高度等信息,而舰载警戒探测设备探测目标的结果信息通常是由距离、方位、仰角、航向和航速等参数,舰艇位置通常用经度和纬度信息表示。显然这几种参数是在不同坐标系下定义的,“经纬高”通常是指WGS-84椭球坐标系,“距离、方位、仰角”是指舰船作战系统的站心坐标系,两者之间要经过一系列的坐标变换才能实现。
3.1 基本坐标系及其变换关系
如图2所示,坐标系oxeyeze为地球直角坐标系(ECEF),x轴在赤道平面内,与零度子午线相交,y轴与x轴、z轴构成右手直角坐标系。地球椭球坐标系(WGS-84),经度B、纬度L的定义如图2所示,高度H通常称为海报高度,定义为与当地椭球面铅垂线的高度。坐标系OENU为地球表面的当地东北天地理坐标系,也是舰船导航系统采用的坐标系。舰艇作战系统的站心坐标系ox1y1z1可以看作是高度为Hp的东北天坐标系,坐标原点通常是与海平面高度差为Hp的点,y1轴平行于地理坐标系北向N轴,水平面ox1y1平行于地理坐标系水平面OEN,z1轴与U轴重合。作战系统中方位角定义为与北向之间按顺时针旋转0~360°之间的夹角,俯仰角定义为与水平面投影之间的夹角,然而目标高度信息采用WGS-84椭球坐标系海拔高度,所以不能采用作战系统直角坐标系中z轴的数值代替目标的高度。警戒探测设备探测到目标信息后,一般都根据导航信息,修正到作战系统站心坐标系下的距离、方位、仰角、航向、航速等目标信息,然后上报给指控系统。
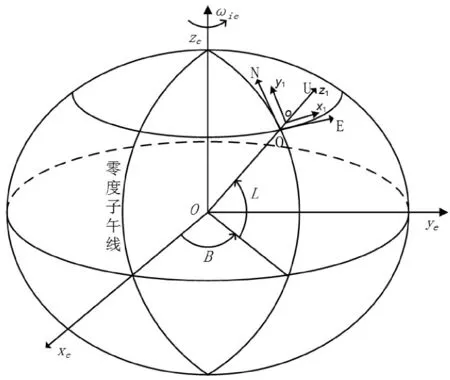
图2 基本坐标系及其相互关系示意图
下面分析涉及到的坐标变换[8]。由经纬高坐标系(WGS-84)变换到地球直角坐标系(ECEF)的公式为
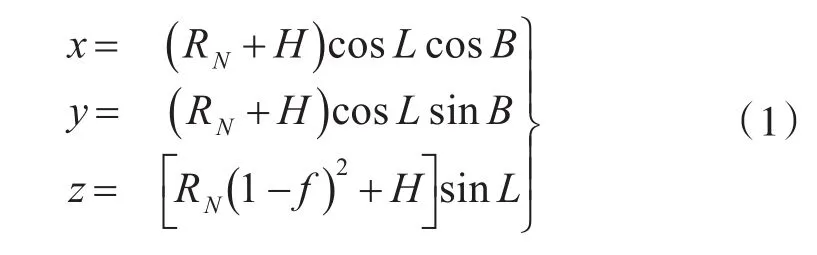
式(1)中RN为卯酉圈半径,f为地球扁率。
由地球直角坐标系(ECEF)转换为经纬高坐标系(WGS-84)没有解析公式,需要迭代计算求得,其公式为
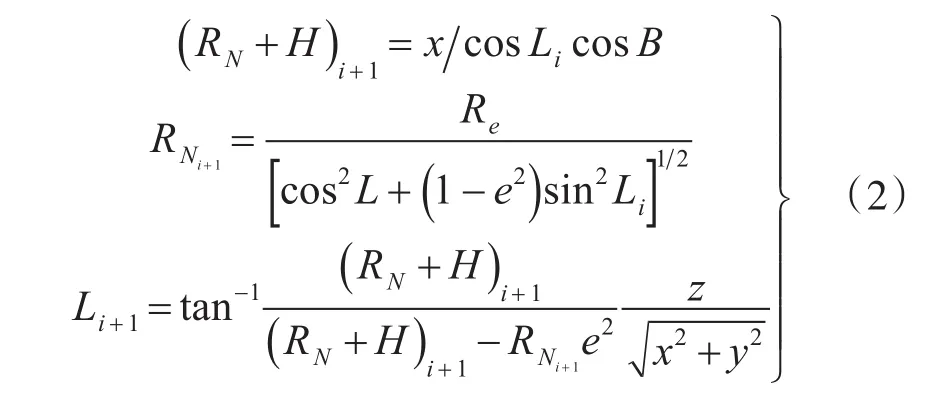
式(2)中e为椭球第一偏心率;注有下标i的值即第i次迭代的值。
地球直角坐标系到地理坐标系的变换矩阵为

地理坐标系到地球直角坐标系的变换矩阵为的逆矩阵。
设警戒探测设备测量的距离、方位、仰角为(r,α,β),则其与作战系统站心坐标系的关系为
设定舰艇作战系统站心坐标系的实时位置信息相对于地球椭球坐标系为(Bp,Lp,Hp),相对于地球直角坐标系为(xpe,ype,zpe),来袭目标在舰艇作战系统站心坐标系的实时位置信息为(xmp,ymp,zmp)。威胁目标航迹解算的基本思路是,依据式(1)~(4),进行变换与逆变换,将航迹分解成在水平面的运动和垂直面的运动两部分,水平面运动部分重点与方位相关,垂直面运动部分重点与仰角相关,分三步进行解算变换[9~11]。第一步,在作战系统站心坐标系下的水平面内,依照航路设计要求解算目标在x1轴、y1轴的运动参数,将解算结果(x1,y1,0)参照(xpe,ype,zpe)变换到地球坐标系(ECEF)坐标值,再将ECEF坐标值变换到地球椭球坐标系(WGS-84),得到对应的经纬高(B1,L1,H1)参数。第二步,根据航路设计要求解算目标垂向运动的高度H2参数,用H2代替第一步解算的H1信息,将水平运动与垂向运动结合成为(B1,L1,H2)信息,将合成后的结果变换到地球坐标系(ECEF),再将其变换到作战系统的站心坐标系,得到来袭目标在舰艇作战系统坐标系的位置信息(xmp,ymp,zmp)。第三步,在作战系统站心坐标系下,根据(xmp,ymp,zmp)求解警戒探测设备测量的距离、方位、仰角、航向、航速等信息。
3.2 典型航迹设计
根据上面论述航迹解算方法,航迹设计主要变成为水平面和垂直面的航迹曲线设计,下面针对向站运动的来袭目标分别论述。
1)直线运动

式(5)中(x,y)为水平面运动方程,式中r0为目标来袭初始距离,α为来袭方位,P为航捷;v为来袭方向的径向速度,a为来袭方向的径向加速度,t为飞行时间,调整v、a与在不同时间段的数值,就实现了变速和变加速运动。H为垂直面运动方程,H0为初始飞行高度。
2)水平蛇形运动
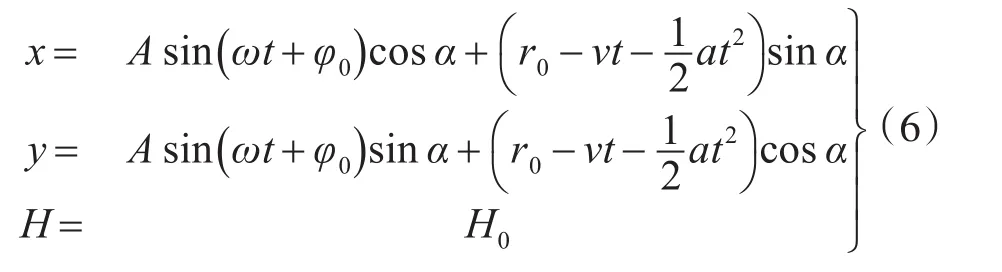
式(6)中A为蛇形机动幅度,ω为蛇形机动频率,φ0为蛇形机动初始相位。航捷可以参照式(5)叠加。
3)垂直蛇形运动
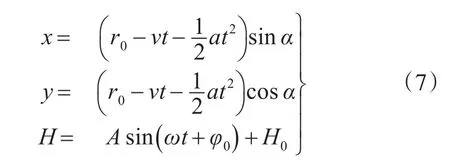
式(7)中A为蛇形机动幅度,ω为蛇形机动频率,φ0为蛇形机动初始相位。航捷可以参照式(5)叠加。
4)大俯冲角运动

式(8)中v为来袭方向的径向速度,a为来袭方向的径向加速度;vh为垂直面下降的垂向速度,ah为垂直面下降的垂向加速度,t为飞行时间,设置vh、ah与在不同时间段的数值,就实现了俯冲角变化速率的调整。航捷可以参照式(5)叠加。
5)模拟反舰导弹爬升降高飞行过程
水平面的运动参考式(4)的(x,y)运动方程,这里重点阐述垂直面的运动,设定爬升和降高段分别由相同的加减速过程组成。
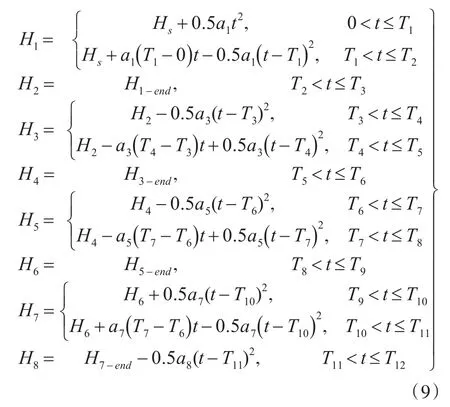
式(9)中,Hs为起始高度。H1~H8分别为一次爬升段、一次平飞段、一次降高段、二次平飞段、二次降高段、三次平飞段、二次爬升段、三次降高俯冲段的高度控制方程,H1,3,5,7-end为爬升或降高段的最终值,a1~a8为每个飞行段的加速度变量,T1~T12为每个飞行段的控制状态变化的时刻变量。合理设置上述3种变量的数值,结合水平面的运动方程,就可以模拟不同弹道轨迹的反舰导弹的爬升降高运动过程,这属于方案弹道的范畴[12]。
本节论述的五种类型的飞行航迹,可以按时序相互组合成为更加复杂的飞行航迹,软件程序中主要设计了8种飞行轨迹样式。
3.3 相位匹配设计
雷达在探测目标的过程中,主要采用连续圆周扫描方式,在雷达显控台上可以看到方位扫描线的圆扫过程。雷达探测目标的策略通常为发现识别后即刻上报,因此由于雷达的扫描过程就对探测目标带来相应时序的变化。可以简化分析认为,在雷达方位扫描线上的目标都能同时探测到,暂且忽略目标前后距离和高度对探测时延的影响,这样就可以重点分析目标方位的不同带来探测时序的变化影响。采取这种近似分析,能够保留影响探测时序的主要因素,由此确定雷达探测到目标的条件为雷达的方位扫描相位与目标相对于舰船作战系统站心坐标系的方位角重合,由这个条件来解算目标运动过程中雷达探测到目标的时序。
以直线运动航迹为例,来分析相位匹配计算的方法过程,选择地理北向N作为雷达扫描相位角和目标方位角的参考基准。
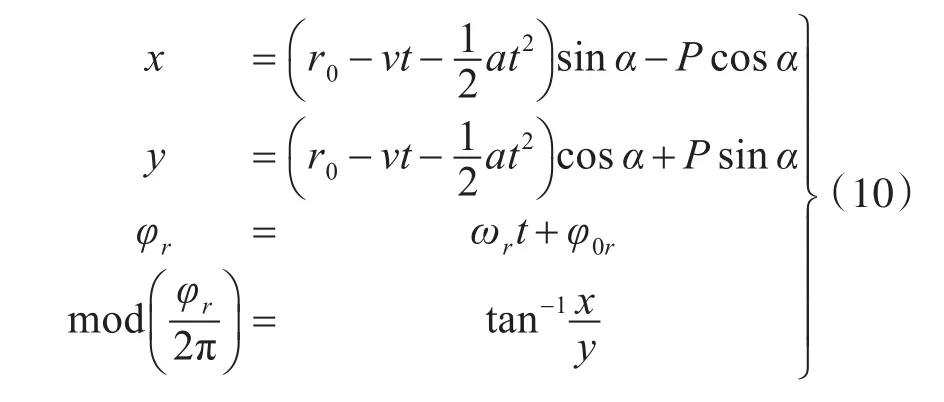
式(10)中φr为雷达扫描相位,φ0r为雷达初始相位,ωr为雷达扫描角速度。式(10)的相位求解方程最后是针对反三角函数的隐函数求解,需要采用迭代求解方法,同时考虑目标在不同象限之间的变化带来的相位突变影响。图3中图(a)为来袭距离30km,航向 210°,航捷 2km,速度 300m/s,高度为10m的导弹目标,其飞行航迹在水平面的投影曲线;图(b)为扫描周期为2s的雷达,在每个扫描周期内测量到目标的时刻曲线,每个扫描周期的起始时刻设为0,雷达初始相位φ0r设为0,可以看到在导弹飞行过程中,雷达探测到目标的时序变化情况。

图3 目标飞行水平投影与雷达探测时序关系图
4 态势设计样例与误差分析
基于前面的方法设计和理论分析,采用Matlab编写了态势数据生成解算软件,按照实装协议生成警戒探测设备数据报文。下面将设计用例和设计误差进行分析,表1为态势目标的主要运动要素参数摘录。
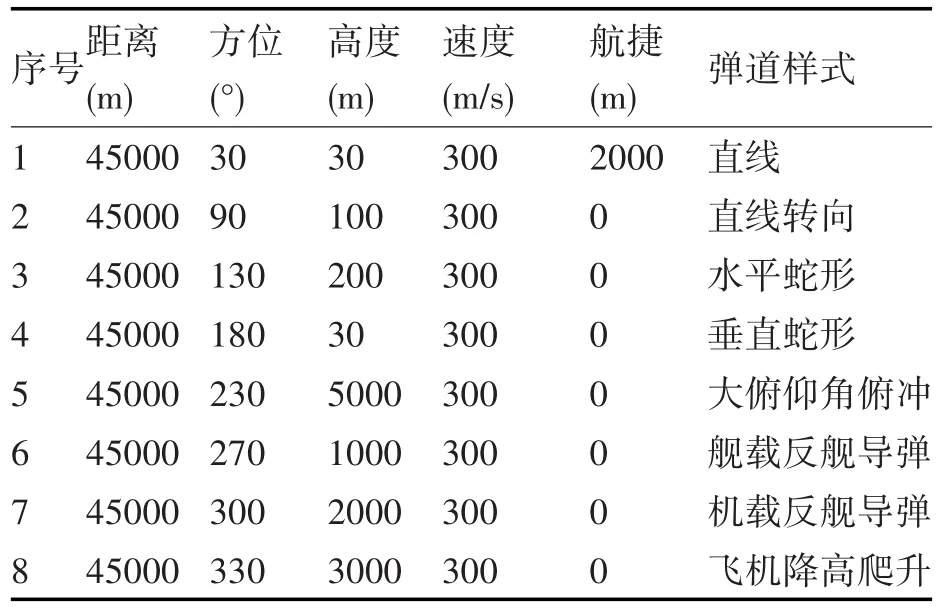
表1 目标运动的主要参数设计(摘录)
根据表1的主要参数要求,计算出目标的航迹曲线如图4所示。来袭目标都是由远及近的向站飞行,其中,图(a)为目标航迹的距离、方位参数绘制的极坐标曲线图,其形状与航迹的水平投影相似;图(b)为目标相对于舰艇作战系统站心坐标系的三维曲线图,可以看出目标航迹的三维空间变化情况;图(c)为目标飞行航迹的海拔高度图,可以看出目标飞行过程的高度变化情况;图(d)为作战系统站心坐标系观测到的z轴参数的变化曲线,与图(c)相比较,可以飞行过程中地球曲率影响带来的z轴参数变化的情况;图(e)为雷达测量目标的仰角曲线图,可以看出不同目标飞行过程中的雷达测量仰角变化情况。
图4显示的是主要的飞行轨迹样式,在试验测试中,基于这几种飞行轨迹样式,模拟不同数量的导弹态势编组和时序关联,就可以构建成复杂的导弹来袭态势。
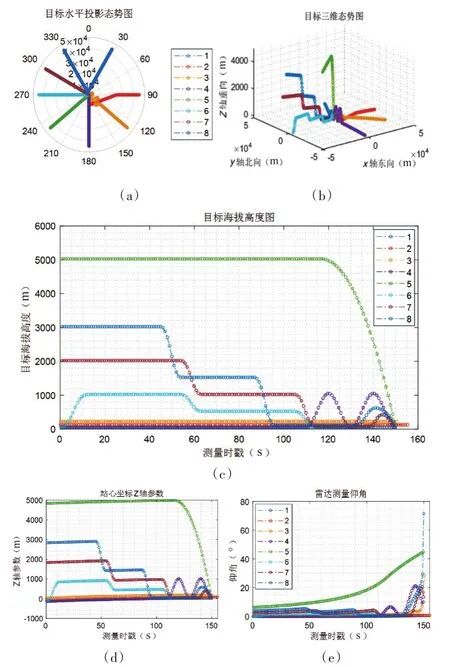
图4 目标航迹样例分析图
分析态势模拟的理论误差,选取目标来袭距离均为200km,来袭方位均为45°,高度分别为30m~9000m的8枚向站飞行的导弹进行对比分析。图5(a)为来袭目标方位角的解算值与设定值之间的偏差曲线,随着高度的增加,误差曲线逐渐下移,解算误差总体上在10-4度量级,雷达报文中对方位和仰角数字化的最低有效位(LSB)为90/214=5.493164×10-3度,所以方位角的解算精度满足试验要求。图5(b)为来袭目标的高度解算值与设定值之间的偏差曲线,在不同高度上的误差规律基本相似,误差由远及近逐渐变小,解算误差总体上在10-7m量级,由此可见这种解算方法,在高度信息上解算精度比较高。
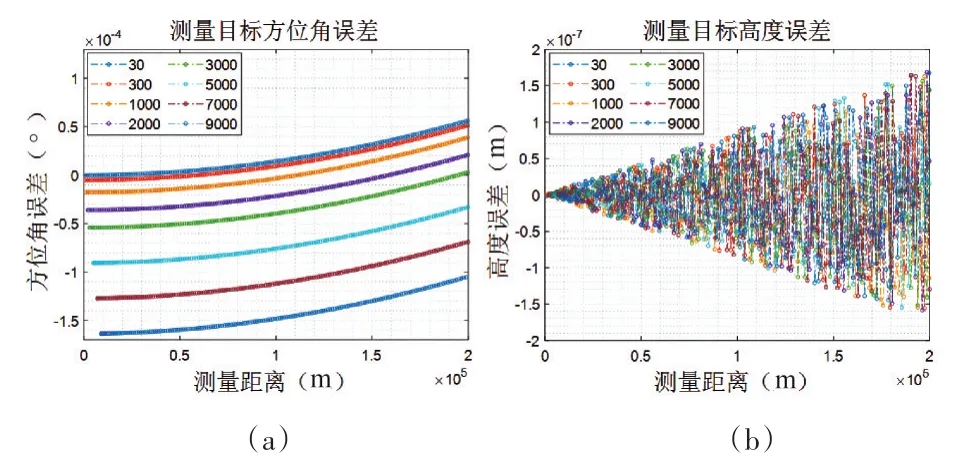
图5 目标航迹方位与高度理论误差分析图
解算生成的态势数据,经过与雷达探测相关和报文协议匹配后,发送给指控系统。依据报文协议进行的数字化量纲转换,带来新的数字化误差,误差来源包括时戳、距离取整,方位角和仰角根据最低有效位(LSB)的换算取整,数字化取整都是按照四舍五入的方法,那么由于仰角数字化带来的高度变化理论误差如式(11)所示。

式中,D为目标距离,Her为仰角数字化带来的高度误差,βLSB为仰角最低有效位。其误差曲线如图6所示,由远及近误差逐渐变小,距离在200km时误差约在±10m之内波动,距离在50km范围内误差基本上在±2m之内波动。

图6 仰角数字化引起的高度理论误差分析图
试验过程中通过录取指控融合与目指数据,武器系统射击诸元的解算数据,经过分析得到目标模拟距离精度达到±2m,航捷精度达到±2m,方位和仰角精度达到最低有效位5.493164×10-3°,高度解算精度符合式(11)和图6的变化规律。
5 结语
本文提出了基于数据驱动的在线仿真方法,编写了数据生成软件和数据推送软件,在某型水面舰艇对空自防御系统性能试验鉴定中,制作了数百个试验态势,驱动了对空自防御系统的目标航迹融合、威胁判断、目指分配、通道组织试验测试,大大提高了试验效率和有效性。同时,制作了实弹射击的目标模拟态势,带动了指控和武器系统的联调检验,为实弹射击的装备技术准备和人员合练提供了保障。在今后的研究中,将进一步加强数据推送过程中的闭环控制,能够根据交战结果对态势数据进行实时调整控制。

