电泳过程车身结构变形仿真方法概述

李鼎 于保君 刘创举 朱学武 曹正林

（1. 中国第一汽车股份有限公司 研发总院，长春130013；2. 汽车振动噪声与安全控制综合技术国家重点实验室，长春130013）

主题词：涂装电泳 有限元法 有限体积法 流固耦合

缩略语

FVM Finite Volume Method

FSI Fluid-Structure Interaction

VOF Volume Of Fluid

FEM Finite Element Method

FSI Fluid-Structure Interaction

CFD Computational Fluid Dynamics

CSD Computational Structural Dynamics

1 前言

电泳涂装工艺一般由涂装前预处理、电泳涂装、电泳后清洗、电泳涂膜的烘干等多道工艺组成，如图1所示。为提高电泳质量和生产节拍，新型翻转线、穿梭机等电泳线逐步被采用，而与之带来的是白车身闭合件的变形、生产过程中车身倾斜和运动装置的脱钩等现象在电泳过程中时有发生。

图1 电泳涂装工艺示意

传统结构强度设计主要考虑整车的碰撞、强度、模态和刚度参数，并未充分考虑白车身在各大工艺过程的应力应变累积情况。而白车身在冲压、焊接工艺设计时，充分考虑了材料、模具、夹具因素的影响，白车身焊接总成整体变形量不大。而当焊接总成进过涂装生产线，由冲压、焊接引入的残余应力，电泳泳池中的流体压力积累的塑性变形，烘烤引入的材料应力释放、热应力变形，最终造成总装时部分车身结构面差较大，无法顺利完成装配。

由于白车身经过涂装后，变形影响因素复杂，因此，在研究此类系统问题时，首先需要将问题进行分解，然后分析不同工序对结构变形的影响，找出设计的薄弱环节，加以优化，再通过多学科仿真工具将全生命周期下的变形情况进行分析和验证。

白车身在电泳槽中的受力主要来自其在泳池中改变姿态而引起的阻力、浸入液面以下受到的浮力、自身重力、工装的约束力，因此可以将模型抽象为求解流体力学及结构力学问题。流体力学部分需要考虑气-液-固3相的交互作用，目前考虑多相流的方法主要是有限体积法（Volume Of Fluid,VOF），由于白车身在泳池中是运动的，因此若采用网格算法进行仿真，则需要采用重叠网格技术。考虑到流体-固体间的交互作用并不显著，因此计算时可以采用单向耦合法进行计算，即先计算不同位置、时间下白车身各零部件表面受到的流体压力情况，再将其作为压力边界条件导入到结构力学计算中。由于白车身钣金为标准固体模型，目前金属弹塑性变形数值模拟中的一种有效数值计算方法为有限元法，将求解对象离散为由各种单元组成的计算模型，计算流体载荷激励下各离散单元非线性位移响应，从而获取钣金残余变形。

当前对电泳过程车身结构变形仿真方法研究尚处于起步阶段。ESS斯太尔工程软件公司提出了一种基于有限差分法对工业EPD 涂层过程进行准确有效的模拟方法[1]。埃尔朗根-纽伦堡大学的Dominik Bartuschat 介绍了一种用于微流控电泳大规模并行直接数值模拟的耦合算法，这种多物理算法采用了流体和离子的欧拉描述，结合了移动带电粒子的拉格朗日表示[2]。卡尔斯鲁厄理工学院用数值方法证明了分段式对电极在不同电位差下可以有效地减少涂层材料的用量，将现有的模型扩展到三维空间中的任意非平面几何[3]。上汽通用五菱汽车股份有限公司应用电泳仿真CAE技术对车身电泳膜厚进行了仿真分析，提升了产品的强度和防腐性能[4]。Institut für Computerphysik利用分子动力学模拟方法研究了聚电解质在平行非带电平板间的电泳拉伸，模拟结果显示，流体动力相互作用的影响，减少了限制板之间的距离[5]。

2 流体侧仿真

电泳过程车身结构流固耦合仿真主要采用计算流体力学计算流体部分。白车身在电泳槽中运动，会产生复杂多变的流体流动特性，电泳液的流动符合湍流流动特性，而车身运动中包含进出槽过程，当中会卷入空气进入车身腔体内部，电泳液在车身表面存在浸润、物质交换的物理化学过程，携带的电泳液在出槽过程会有流淌现象。因此白车身电泳槽的运动过程实质上是一个多相流问题。根据具体工程应用，可以将电泳液定义为流体的液相，空气定义为气相，整个流动过程符合气液2相流计算模型。

2.1 有限体积法网格化理论

有限体积法（Finite Volume Method，FVM）是近年发展非常迅速的一种离散化方法，其特点是计算效率高，目前在流体领域得到了广泛的应用。其基本思路是：将计算区域划分为网格，并使每个网格点周围有一个互不重复的控制体积；将待解的微分方程（控制方程）对每一个控制体积分，从而得到一组离散方程。其中的未知数是网格点上的因变量，为了求出控制体的积分，必须假定因变量值在网格点之间的变化规律。从积分区域的选取方法看来，有限体积法属于加权余量法中的子域法，从未知解的近似方法看来，有限体积法属于采用局部近似的离散方法。北京航空航天大学流体力学研究所的朱自强给出了一种生成分区对接网格和Euler 方程分区解，以二维多段翼型为对象分别讨论了分区重叠结构网格方法、非结构网格方法和自适应的笛卡尔网格法[6]。杨建宏通过有限元空间和有限体积元空间的一种双射投影，得到了不可压缩流问题低次等阶稳定有限体积元方法[7]。D.G.Roychowdhury 讨论了计算流体力学中的各种控制方程及其推导，以及偏微分方程描述边界条件的物理和数学意义[8]。

对于电泳过程车身高度复杂的几何，捕捉此几何可能比较困难。在这类情况下，包面可用于简化和捕捉复杂几何的水密表示。无论是否使用包面，通常都使用表面重构来重构几何的初始表面。几何的初始表面通常由许多三角表面组成。此三角形化也称为网格化，通常包含高度偏斜的三角形，不适用于生成高质量体网格。重构通过生成尺寸更均匀的三角形提高这些表面的整体质量，此方法最适合网格模型。然后，使用重构表面作为体网格的基础。

2.2 多相流仿真方法

目前在多相流计算中，如果采用网格算法，通常采用欧拉-欧拉法和欧拉-拉格朗日法2种方法，其中欧拉-欧拉法常用流体体积模型（VOF）、混合物模型及欧拉模型，欧拉-拉格朗日法常用离散相模型。

VOF 模型是一种在固定欧拉网格下表面追踪的方法，它通过研究网格单元中流体和网格体积分数来确定自由面，追踪流体的变化，而非追踪自由液面上质点的运动。在计算过程中，利用各流体的体积分数为计算参数，在一个动量方程中进行求解，把每个时刻各流体所占的体积比都记录下来。

体积追踪/交界面捕捉法非常适用于模拟具有大尺度交界面的分层多相流体。必须注意的是，计算网格单元的尺寸在将交界面分类为大尺度还是小尺度时至关重要。由于体积追踪/交界面捕捉法依赖于完全求解交界面，因此在离散流态建模精度同样重要的多尺度流体模拟中使用这些方法会导致成本过高。流体体积(Volume Of Fluid,VOF) 多相模型实施属于交界面捕捉方法系列，可预测不混溶相交界面的分布和移动。此建模方法假设网格分辨率足以求解相之间的交界面位置和形状。

交界面的相分布和位置由相体积分数∝i的场来描述。相i的体积分数定义如式（1）：

式中，Vi为为网格单元中相i的体积，V为网格单元的体积。

网格单元中所有相的体积分数总和必须是式（2）：

式中，N为总相数；∝i=0表示网格单元完全没有相i；∝i=1 表示网格单元完全由相i填充；0＜∝i＜1表示2个极限之间的值存在相间交界面i。

包含交界面的网格单元中计算的材料属性依赖于组成流体的材料属性。同一包含交界面的网格单元中的流体被视为混合物，其中混合物的密度、粘度及比热如式（3）（4）（5）：

式中，ρi为相i密度，μi为相i动力粘度，(Cp)i相i比热。

体积分数传输方程相i的分布由相质量守恒方程驱动，如式（6）：

式中，a为表面积矢量，v为混合（质量平均）速度，vd,t为扩散速度，Sai为相i的用户自定义源项为相密度ρi的材料或拉格朗日导数。

计算采用如下所示计算相体积分数：

1）存在2 个VOF 相时，仅对第1 个相求解体积分数传输。在每个网格单元中，调整第2个相的体积分数，使这2个相的体积分数总和等于1。

2）存在3个或更多VOF相时，对所有相求解体积分数传输。然后，根据每个网格单元中的所有相的体积分数总和标准化每个相的体积分数。

连续性方程所有相的总质量守恒方程由式（7）给出：

式中，S为与相源项相关的质量源项，如式（8）所示：

通过由式（3）给出的密度来解释对流体混合物组成相的体积分数的依赖性。

动量方程及能量方程如式（9）式（10）所示：

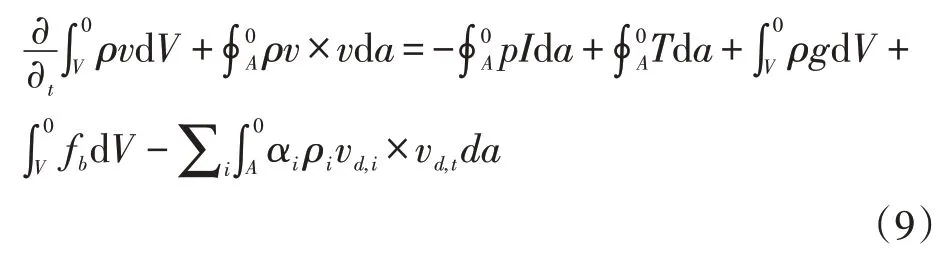
式中，p为压力，I为单位张量，T为应力张量，fb为体积力矢量。

工程中关注的大多数流体流都具有不规则的波动流量。此类波动通常尺度小但频率高，要在时间和空间上对其求解，需要高昂的计算成本。可以不求解湍流的精确控制方程（直接数值模拟），改为求解平均量或滤波量来近似小波动结构的影响，这样成本较低。各种湍流模型为此类结构的建模提供了不同的方法。

2.3 重叠网格技术

由于白车身在电泳槽中是运动的，如果采用网格重构技术，网格计算量很大而且会造成后期结构有限元计算网格节点不统一。因此需要使用重叠网格技术。重叠网格也称作“嵌套”网格，用于离散具有以任意方式相互重叠的多个不同网格的计算域。这些网格在处理涉及多个体或移动体的问题时以及优化研究中最为有用。Tapan K. Sengupta 通过计算二维Navier-Stokes 方程，使用单块结构和重叠网格来求解圆柱绕流，利用相对较少的网格点捕获了该布置的已知流动特性[9]。

中国船舶科学研究中心的赵发明采用RANS方法和重叠网格计算了带自由液面的船舶绕流问题，描述了重叠网格和单相Level Set 自由液面模拟方法的数学模型及求解过程[10]。上海交通大学船舶海洋与建筑工程学院的王建华采用重叠网格技术开发的多功能水动力学求解器naoe-FOAM-SJTU，对标准船模DTMB5512裸船体在平面运动机构(PMM)控制作用下对纯摇首运动进行了数值模拟[11]。海军工程大学的周广礼以Suboff标模为研究对象，基于RANS方程、VOF模型及重叠网格技术，建立了潜艇应急上浮运动的数值预报方法[12]。

在大多数情况下，使用重叠网格不需要在生成初始网格之后进行任何网格修改，比标准网格化方法更灵活。任何涉及重叠网格的研究都具有封闭整个求解域的背景区域，以及包含域中的体的一个或更多较小区域（图2）。

图2 重叠网格示意

在重叠网格中，网格单元分组为活动、不活动或受体网格单元。在活动网格单元中，将对离散控制方程进行求解。在不活动网格单元中，不会对任何方程进行求解，但是如果重叠区域在移动，这些网格单元可以变为活动状态。受体网格单元可分离背景区域中的活动和不活动网格单元，并与重叠区域中的重叠边界相连接。受体网格单元用于耦合2个重叠网格上的求解。一个网格的供体网格单元处的变量值，通过插值表示其他网格中受体网格单元处的变量值。供体网格单元是其他网格中最靠近受体网格单元的活动网格单元。

将同时为所有区域中的所有活动网格单元计算求解，即网格为隐式耦合。当引用离散方程中一个网格的受体网格单元中的变量值时，将使用其他网格中供体网格。

3 固体侧仿真

电泳过程中，车身变形是由液体冲击及车身自身运动导致，因此需将流体侧计算获得的不同时刻下的流体压力值，映射到结构计算的有限元网格上，作为压力边界条件计算整个过程中白车身的弹塑性变形情况。

3.1 有限元法网格化理论

有限元法（Finite Element Method,FEM）是广泛应用的固体力学数值计算方法。有限元法是将一个连续的求解域任意分成适当形状的许多微小单元，并于各小单元分片构造插值函数，然后根据极值原理（变分或加权余量法），将问题的控制方程转化为所有单元上的有限元方程，把总体的极值作为个单元极值之和，即将局部单元总体合成，形成嵌入了指定边界条件的代数方程组，求解该方程组就得到各节点上待求的函数值。有限元法的基础是极值原理和划分插值，它吸收了有限差分法中离散处理的内核，又采用了变分计算中选择逼近函数并对区域积分的合理方法，是这2 类方法相互结合，取长补短发展的结果。它具有广泛的适应性，特别适用于几何及物理条件比较复杂的问题，而且便于程序的标准化。Nathan Mendes 在Basics in Practical Finite-Element Method 一书中详细介绍了有限元法及其应用[13]。庄茁在基于ABAQUS 的有限元分析和应用中详细介绍了有限元的基本理论和数值计算方法，并对相关例题进行了讨论研究[14]。杜平安详细介绍了划分有限元网格时应考虑的一些基本原则，包括网格的数量、疏密、阶次、质量、分界点、布局、编号等[15]。

3.2 多体动力学仿真

白车身在电泳槽中的运动模式与涂装工艺相关，如图3所示。在自身重力的作用下，不同的运动模式对车身变形有相应的影响，因此在模拟电泳过程固体侧变形时，需考虑动力学影响。

图3 车身电泳过程示意

应用拉格朗日待定乘子法，动力学方程如式（11）：

式中，Φq为约束方程雅克比矩阵；M为质量矩阵；λ为拉格朗日乘子；q̈为加速度；F(q,q̇,t)为作用力；γ为加速度公式中二阶导数项。

其中，系统约束方程为式（12）：

求约束方程广义坐标的偏微分，可得到约束方程雅克比矩阵Φq：

速度方程为式（14）

加速度方程为式（15）

由加速度方程得到的拉格朗日乘子γ为式（16）

3.3 结构力学非线性仿真

与流体方程不同，固体应力在拉格朗日架构中求解，网格依据材料中的材料点。这意味着特定网格单元中的质量将在变形时保持不变，因为它在物理上代表相同的材料。此网格单元质量由材料原始密度与原始体积的乘积来确定。因此，变形状态下的密度是原始质量除以网格单元的当前体积。

固体力学用于描述固体连续体对应用负载的响应行为。应用负载包括体积力、表面负载、点力或固体温度变化导致的热负载。应用负载会在结构中产生应力场，并且可能导致结构位移从初始未变形配置到变形配置。

应用的负载可导致固体结构产生从初始配置到变形配置的位移。总位移由刚体运动和体中各点的相对位移（决定固体结构的变形）共同组成，如图4所示。

图4 各节点总位移示意[16]

如果未变形配置中材料点的位置为X，且此点相对于变形配置的位移为u(X,t)，则该材料点在变形配置中的位置为式（17）：

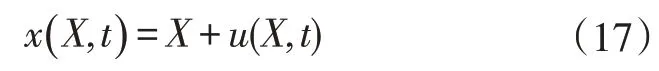
采用分量形式，位移可以表示为式（18）：

刚体的位移场完全由单个位移矢量定义。可变形体的位移场由其材料点的位移矢量集定义。

应力是作用于表面的单位面积力的度量。在固体结构中，外力或温度变化会产生可能导致固体结构运动和变形的应力场。而阻碍结构变形的内力也会引起可将结构恢复到原始未变形状态的内部弹性应力。一些材料还具有内置应力，这种应力在没有作用力和变形时就已存在。

一般情况下，作用于体的平面截面上的应力由矢量（称作应力矢量或拉力）定义如式（19）：

式中，F为作用于平面的力，A为平面的面积。

在任意点处，应力是单位面积上的力，应力状态完全由与3个通过该点且相互垂直的平面关联的应力矢量定义。因此，任何平面上的任何点处的应力状态均通过式（20）形式的二阶张量定义：固体侧计算得到的离散网格节点坐标与原始坐标之差即为车身在电泳过程中的残余变形。

4 流固耦合仿真方法研究

流固耦合(Fluid-Structure Interaction,FSI)是目前很多领域研究的热点和难点之一，与国外相比，国内在该方面的研究相对滞后或片面。Lúcia Armiliato Sangalli 提出了一种用于颤振失稳主动控制桥梁数值模拟的流固耦合格式，采用2 步Taylor-Galerkin 显式方法和任意拉格朗日-欧拉（ALE）描述求解了流动基本方程[17]。Andreas Hessenthaler 建立了16 个独立的分析解决方案，能够在二维和三维、静态和瞬态情况以及线性和超弹性固体材料中实现法FSI 分析，证明了这些解决方案在分析收敛行为方面的实用性[18]。陈锋绍了流固耦合的基本理论和算法，包括流固耦合问题的基本概念与耦合机理的分类，探讨了强耦合和弱耦合算法的计算流程与适用范围，阐述了任意拉格朗日欧拉法、无网格法、特征线分离算法及基于流动条件插值的有限元法等流固耦合分析方法[19]。王建军详细描述了自由液面大晃动的流固耦合问题的性质和特点，讨论了交替求解方法及其对求解此类问题的特别适应性[20]。Yue Qian-bei 提出了一种基于子迭代回路的弱耦合算法，对弹性管的固有频率与静流频率之比的影响进行了深入的数值研究[21]。José A.González提出了一种考虑沸腾和冷凝相变的水蒸汽能量系统瞬态模拟的流固耦合有限元方法，利用Crank-Nicolson 显式隐式时间积分方法，提升了分析精度和稳定性[22]。

4.1 有限元法网流固耦合分类

流固耦合问题从物理上可分为2 类：第1 类是耦合仅作用在2相交界面上，由耦合面上的动力学平衡条件及运动学协调条件来引入方程上的耦合，如气动弹性、水动弹性问题等；第2类是二相遇部分或全部重叠在一起，如渗流问题，其耦合效应通过描述问题的微分方程体现。流固耦合问题从控制方程解法上可分为直接求解(Direct)的强耦合(Strong coupling)和分区迭代求解(Partitioned)的弱耦合(Loose coupling)。所谓强耦合，是将流体域、固体域和耦合作用构造在同一控制方程中，在同一时间步内，同时求解所有变量。由于固体方程与流体方程存在很大的差异，联立求解困难重重。目前还没有一款商业软件可以求解强流固耦合问题。弱耦合是在每一时间步内，分别依次对CFD方程和CSD方程求解,通过中介交换固体域和流体域的计算结果数据,从而实现耦合求解。目前，流固耦合基本上都是采用弱耦合。由于存在时间差，所以与现实情况存在一定的误差。单向耦合与双向耦合主要是针对弱耦合求解。

考虑到车身电泳过程流体-固体间的交互作用并不显著，且车身结构较为复杂，因此，计算时采用单向弱耦合法进行计算，即先计算不同位置、时间下白车身各零部件表面受到的流体压力情况，再将其作为压力边界条件导入到结构力学计算中，最终获得白车身的整体弹塑性变形结果。

4.2 分类界面信息传递与网格匹配

流固耦合的关键是界面信息传递，其原理很简单，即流体域和固体域在边界上对应质点间满足位移协调ds=df和作用力的平衡条件fs=ff。但进行数值模拟时，由于CFD 和CSD 对计算网格要求的不同，导致耦合界面上的网格不匹配，节点多数情况下并不重合，从而不能直接进行数据的交换，这就需要流固界面上节点采用一定的信息映射方法。

通常CFD计算要求的网格密度比CSD要密得多，由此产生耦合界面上2套非匹配网格之间的数据传递问题,在数学上是一个双向插值问题。结构将在流体荷载作用下发生的变形通过耦合界面由CSD 网格传递给CFD 网格，CFD 求解器在新状态下求解流场，再将流体荷载通过耦合界面传递给CSD 网格。可以通过采用一定的映射算子来进行计算，将流体节点应力首先映射到固体节点，然后通过积分(采用固体边界的差值函数)至固体节点力，再将计算出固体模型的节点力，在有限元步骤里作为自然边界条件。由于固体节点力是流体速度和压强的函数，因此固体域的结构离散方程里包括了流域求解变量。

5 结束语

综上所述，电泳过程车身结构变形仿真分析尚处于理论阶段，未有全面系统的流程与试验对比作为支撑，少数关于电泳过程车身的仿真仍主要以涂层本身为研究对象，且主要为静态过程。本文所述的电泳过程车身结构变形预期仿真方法会在以下3点存在较大挑战：

（1）车身电泳过程中边界条件，包括工艺操作参数设定的整体移动速度、翻转速度、喷嘴流场均会影响白车身水动力CFD分析结果，且车身在出水时会产生白车身集液问题，因此边界条件的准确度及选用的算法模型将会对结果精度有较大影响。

（2）由于白车身在电泳槽中是运动的，因此与采用重叠网格技术，而白车身与开闭件结构较为复杂且有较多孔隙，结构的离散化规则会导致不同的结果响应，且会影响相应的计算时间。

（3）由于流体侧与固体侧分别采用有限体积法与有限元法进行求解，因此分类界面信息传递与网格匹配中，不同的映射算子、传递迭代步长、耦合策略等将会对固体域的结构离散方程求解有较大影响，如何优化上述参数需要进行深入研究。