光刻调焦调平测量系统算法比较研究∗
范 伟 李世光 武志鹏 段 晨 宗明成
(1.中国科学院微电子研究所 北京 100029)
(2.中国科学院大学 北京 100049)
1 引言
光刻机是大规模集成电路芯片制造的核心设备,对焦控制[1]是保障光刻机成像质量、光刻工艺窗口和产品良率的重要技术保障,调焦调平测量系统是光刻机对焦控制的核心部件。调焦调平测量系统的数据处理精度影响光刻机的对焦控制性能[2],计算速度影响光刻机的产能[3],因此需要综合考虑这两个因素。本文对比分析多项式拟合算法(polynomial fitting)[4]、RF(random forest)算法[5~6]和XGBoost(extreme gradient boosting)算法[7]在调焦调平测量系统中的测量精度与计算耗时,提出适用于光刻调焦调平测量系统的拟合算法。
2 调焦调平测量系统与实验测量
本实验室搭建的调焦调平测量系统[8]基于光学三角法测量硅片高度,探测器接收到的O光与E光信号[9]为
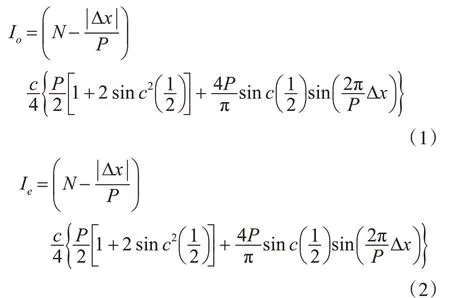
式中,N为光栅狭缝个数,P是矩形光栅周期,Δx是硅片高度变化为h时从投影光栅出射的光束中心位置在探测光栅处产生的偏移,c是(偏振片+分光晶体)组件的透射率。
对O光和E光信号进行归一化差分处理[9]后得到hraw,即当硅片在调焦调平测量系统零位附近± 1.25μm范围内变化时,hraw随h近似线性变化。光栅狭缝个数为29,周期为30,采样点数为7520个,仿真生成该范围内连续扫描35次的hraw与h数据,如图1所示。通过拟合算法得到硅片表面高度h随hraw的变化关系模型后,即可通过hraw计算得到硅片表面拟合高度hfit。不同的拟合算法得到的这种变化关系模型具有不同的计算精度和速度。
使用基于Python的Scikit-learn工具包对数据进行处理。将hraw与h输入到模型中可得拟合算法模型,将hraw代入拟合算法模型中即可得到硅片表面高度拟合值hfit,记录获得hfit的耗时,计算硅片表面真实高度h与拟合高度hfit的差herror及其3σ值,即,式中μ为herror的均值,N为数据个数。

图1 实验数据
3 本研究采用的拟合算法
本研究采用3种拟合算法:多项式拟合、RF算法和XGBoost。多项式拟合算法是曲线拟合的基本方法,其形式简单且易于工程实现。RF算法是Bagging集成算法[10]的典型代表,通过并联多个基学习器的结果提高精度。XGBoost算法是Boosting集成算法的典型代表,通过串联多个基学习器的结果提高精度。
3.1 多项式拟合算法
多项式拟合函数为多次方程,其形式为
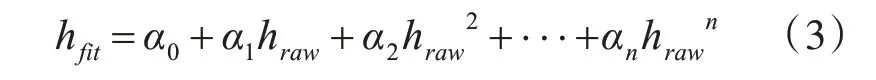
式中αi为拟合系数,由最小二乘法确定,即最小化
3.2 RF算法
RF由多个决策树(decision tree)并联组合而成,对单个决策树的结果进行结合后作为RF集成方法的结果,算法主要参数为决策树的总个数n与单个决策树的最大深度(max depth),其框架示意如图2所示。
决策树在构建过程中采用平方误差准则(square error criterion)进行特征选择构建二叉树。对于输入样本(xi,yi),单个决策树的模型[11]如下:
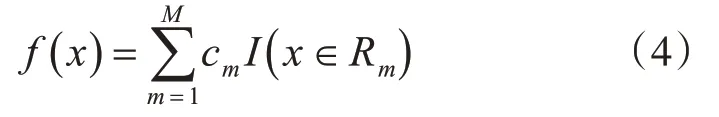
式中,R1,R2,…,RM为输入空间可划分成的M个区域,Cm为每个区域Rm上的输出值。
3.3 XGBoost算法
XGBoost由多个决策树串联组合而成,前一个决策树的输出结果作为输入传送到下一个决策树中,经过多个决策树得的输出作为RF集成方法的结果,主要参数为决策树的总个数n与单个决策树的最大深度(max depth),其框架示意如图3所示。

图3 XGBoost算法框架示意图
对于给定N个样本、m个特征的数据集D={(xi,yi)}(|D|=N,xi∈Rm,yi∈R),集成树模型使用K棵CART决策树结果的累加值作为预测值[6]:

式中,fk(xi)是样本(xi,yi)在第k棵树的叶子结点上的权重。F={f(x)=wq(x)}(q:Rm→T,w∈RT),q表示将样本映射到相应叶子结点的树结构,T表示树中叶子结点的个数。wi表示第i个叶子结点的评分(score)。
4 仿真结果与分析
将图1原始数据转化成hraw-h曲线,如图4(a)曲线所示。使用多项式、RF和XGBoost算法对该曲线进行拟合,拟合高度hfit分别如图4(a)曲线所示。3种算法计算得到的hfit与h相减后得到拟合误差,如图4(b)~(d)所示。误差图中的水平线纵坐标值对应误差的±3σ值,多项式拟合误差为0.001nm,RF拟合误差为0,XGBoost拟合误差为10.789nm。其中,RF算法拟合误差为0的原因将在4.2节分析。
图4展示的是某特定参数下不同算法的拟合高度、误差和3σ值。实际上,算法的拟合精度3σ与计算耗时会随拟合参数变化而变化,下文对此变化关系进行仿真与实验分析,并说明图4(b)~(d)的拟合参数设置过程。

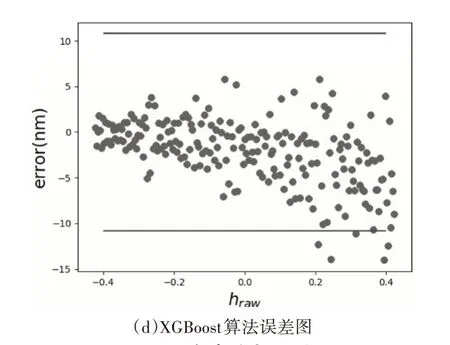
图4 拟合高度与误差图
4.1 多项式拟合算法分析
改变多项式拟合阶数,对图4(a)中hraw-h曲线进行拟合,拟合误差的3σ值如图5所示,小图为局部放大图。随着拟合阶数的增加,拟合误差的3σ值不断减小。多次统计发现多项式拟合算法计算耗时总小于1ms,这是因为多项式拟合算法简单,时间复杂度小。
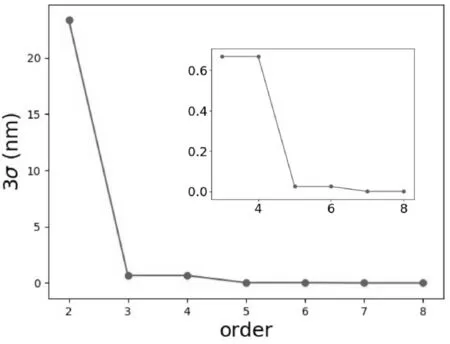
图5 多项式拟合算法3σ 值随阶数变化图
4.2 RF拟合算法分析
RF算法中影响精度与计算耗时的主要因素是决策树的最大深度与决策树的个数n,使用网格搜索[12]方法改变这两个参数,拟合误差的3σ值与计算耗时如图6所示。
由图6(a)可知,RF算法中,决策树的最大深度对拟合误差有较大影响,决策树个数的变化对拟合误差影响小。这是因为RF算法采用的并行计算策略在决策树增多时可以降低拟合方差,拟合误差的减少主要依靠单个决策树的最大深度,决策树的最大深度越深,拟合误差越小。由图6(b)可知,计算耗时随决策树个数与决策树的最大深度的增加呈增加趋势,模型复杂度的提升会造成计算时长的增加。
在RF算法中,单个决策树的输入为hraw,输出为该决策树得到的拟合高度hfit,由于仿真数据是没有噪声影响的采样点序列,当决策树最大深度增加时,算法对数据的拟合能力不断增强,算法能获得hraw序列和h序列间的一一对应关系,如同构建了键为hraw,值为h的映射表,通过查询hraw,可直接得到对应的h,因此图4(c)中误差为0。
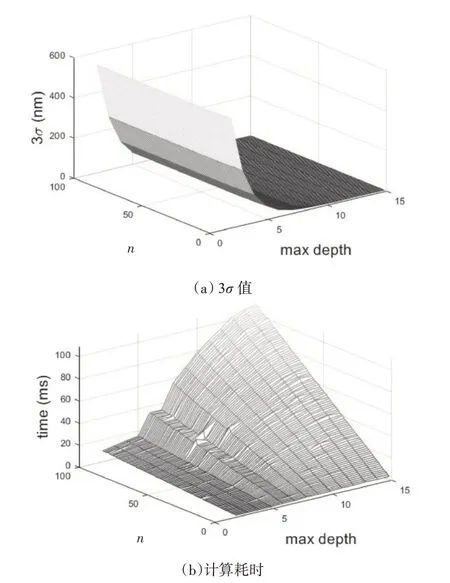
图6 RF算法3σ 值与计算耗时图
4.3 XGBoost拟合算法分析
改变决策树的个数和最大深度,XGBoost算法拟合误差的3σ值与计算耗时如图7所示。

图7 XGBoost算法3σ 值与计算耗时图
由图7(a)可知XGBoost算法中测量精度随决策树的最大深度与决策树的个数增加而增加。由图7(b)可知计算耗时随决策树个数n与决策树最大深度的增加而增加。RF算法中各决策树相互独立,而XGBoost算法中,前一个决策树的输出作为下一个决策树的输入,hfit为各个决策树的输出加权和。XGBoost与RF算法计算机制的不同,使得尽管RF和XGBoost均采用决策树个数和最大深度作为拟合参数,两者的拟合精度有较大差异。
4.4 拟合算法对比分析
分别改变多项式拟合算法的阶数、RF和XG⁃Boost算法中的最大深度与决策树个数,对图1所示的数据重新进行拟合。当多项式拟合阶数在2~8范围内变化,决策树个数在1~100范围内变化,最大深度在2~15范围内变化时,得到不同参数下的3σ值。在光刻机中,为了兼顾对焦精度和产能,必须兼顾算法的拟合精度与拟合时间,最终得到一个优化方案。因此在参数选取时,设定两个约束条件:1)计算当前参数与前一次参数下的3σ差值Δ3σ,只选取保证Δ3σ<0.3nm的参数。其中,0.3nm是个拟合实践值,当Δ3σ<0.3nm时,可以认为拟合精度基本维持在最高精度,不随参数递增而提高;2)设定计算耗时小于某给定计算时间。这是因为计算耗时越长,拟合精度通常更好,而工程实践一般不允许拟合时间过长。对于多项式拟合算法,在8阶拟合范围内,计算时间均小于1ms,满足Δ3σ<0.3nm的阶数有4,6,7,8。拟合残差3σ最小时(0.001nm)对应的阶数为7和8,由于7阶对应的计算时间短,因此选择7阶作为多项式拟合的阶数。对于RF算法和XGBoost算法,约束条件1)具体为:当前参数对(i,j)得到的3σ值(i为决策树个数n,j为最大深度max depth),与参数对(i-1,j)和(i,j-1)得到的3σ值的差异都满足Δ3σ<0.3nm 。由图6和图7可知,同时满足上述两个约束条件的(i,j)通常不唯一,为了得到最佳拟合效果,选取拟合残差3σ最小时所对应的那组(i,j)作为该曲线的拟合参数。绘制不同计算时间下的3σ曲线如图8所示,小图为局部放大图。图4表示的是当计算时间为3ms时(图8矩形框区域所示),3类算法的拟合高度与误差曲线,此时多项式拟合为7阶;RF决策树个数为3,最大深度为8;XGBoost决策树个数为8,最大深度为10。
由图8可知,多项式拟合算法精度随时间变化不敏感,7阶多项式拟合的3σ值为0.001nm,RF算法和XGBoost算法精度随计算时间的增加迅速提升,RF算法在2ms时,对仿真数据完全拟合,误差为0,XFBoost算法在5ms时,拟合精度基本趋于稳定,为0.6nm。在计算时间比较关键的情况下,例如计算时间为1ms,多项式拟合算法精度最高,其次为RF算法。
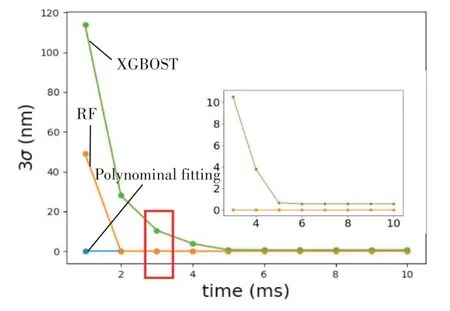
图8 不同算法3σ 值随给定计算时间的变化图
5 实验结果与分析
为了验证上述3种算法在实际数据中的有效性,采集3组实验数据,按4.4节中所示流程获得不同算法的3σ值随给定计算时间的变化,如图9所示。3种算法随计算时间变化的趋势与图8相同,多项式拟合精度随时间变化不敏感,RF算法和XGBoost算法精度随计算时间的增加而迅速提升,相对于XGBoost算法,RF算法可以更快地稳定到比较高的精度。但总体上,3σ值均有所增加,RF和XGBoost算法趋于稳定的时间有所延长,RF算法精度在3ms时超越多项式拟合算法,而XGBoost在5ms时拟合精度超越多项式拟合算法,且RF算法在处理实际数据上,拟合精度略优于XGBoost算法。
从图9中可知,3次实验在给定计算时间为10ms时,多项式拟合算法的3σ值分别为14.1nm、25.6nm和17.4nm;RF算法的3σ值分别为7.8nm、24.8nm和13.9nm;XGBoost算法的3σ值分别为9.2nm、24.7nm和14.4nm。在给定1ms的计算时间下,多项式拟合算法精度最高。图9中的3σ值大于仿真结果中对应的数值,这是因为实验环境不理想,存在环境噪声,实验系统自身存在10nm的重复性误差等。随给定计算时间增加,RF算法与XG⁃Boost算法拟合精度不断提升并超越多项式拟合算法,这是因为多项式拟合基于最小二乘法,因此对噪声比较敏感,而基于决策树的RF算法与XG⁃Boost算法对噪声有较好的鲁棒性。
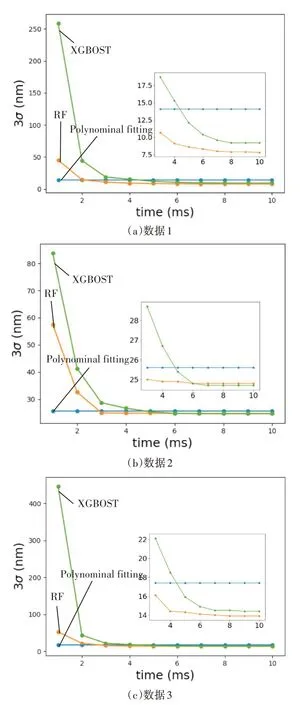
图9 不同算法3σ 值随给定计算时间的变化图
6 结语
本文通过仿真与实验对比分析了多项式拟合、RF算法和XGBoost算法在光刻调焦调平测量系统中数据处理的精度与速度。仿真与实验结果表明,多项式拟合精度随时间变化不敏感,RF算法和XGBoost算法精度随计算时间的增加而迅速提升。对于不存在噪声的仿真数据,7阶多项式拟合的3σ值固定在0.001nm;RF算法在2ms时,算法对仿真数据完全拟合,误差为0;XGBoost算法在5ms时,拟合精度基本趋于稳定,为0.6nm。对于存在噪声的实验数据,RF算法相对于XGBoost算法可以更快地稳定到比较高的精度,且拟合精度略优于XGBoost算法。随计算时间的增加,RF算法与XG⁃Boost算法拟合精度不断提升并分别于3ms和5ms超越多项式拟合算法,这是因为多项式拟合基于最小二乘法,因此对噪声比较敏感,而基于决策树的RF算法与XGBoost算法对噪声有较好的鲁棒性。在计算时间比较关键的情况下,例如计算时间为1ms,多项式拟合算法精度最高,其次为RF算法。在光刻机中,为了兼顾对焦精度和产能,必须兼顾算法的拟合精度与拟合时间。在处理实际数据时,RF和XGBoost拟合精度尽管在3ms~5ms以后比多项式拟合精度略有提高,但提高有限,而3ms~5ms处理一组数据对光刻机产能而言难以容忍。综合考虑拟合精度与计算时间,调焦调平测量系统选用多项式拟合算法较为合适。

