基于逻辑运算的离散人工蜂群优化双聚类算法∗

马 卫 朱 娴

（1.南京旅游职业学院酒店管理学院 南京 211100）

（2.南京大学计算机科学与技术系计算机软件新技术国家重点实验室 南京 210093）

（3.南京理工大学紫金学院计算机学院 南京 210046）

1 引言

DNA微阵列技术可以同时测量成千上万个基因的表达水平，通过不同实验条件下的重复实验产生数百个实验资料。这种技术通常会产生大量的原始数据，通过分析提取有用的信息，对医学临床诊断、揭示疾病发生机制等方面起着重要作用。

为了挖掘基因表达数据中基因和实验条件相互表达的局部信息，Cheng和Church［1］提出了双聚类CC算法，运用贪心策略同时在基因和实验条件两个维度上搜索双聚类。随后，可重叠、随机搜索和多目标进化等双聚类算法不断提出。

Yang等［2］提出了概率算法（FLOC），在CC算法的基础上进行了改进，解决了每次迭代只能发现单个双聚类的问题，能够发现可重叠的双聚类。群体智能算法是近三十年非常普遍的数据挖掘方法，模拟退火算法、遗传算法、粒子群算法、蚁群算法等均被应用于双聚类。Chakraborty［3］初始化双聚类种子采用模拟退火法随机搜索双聚类，使得产生双聚类结果达到全局最优。Wolf等［4］采用模拟退火法在全局搜索的基础上进行了改进。多目标进化双聚类算法是目前双聚类优化采用最多的算法。Mitra等［5］采用经典非支配排序遗传算法优化双聚类，提出了具有多目标进化双聚类框架。刘万军［6］提出了微阵列多目标优化双聚类，分别用多目标粒子群、多目标蚁群、多目标人工免疫等多目标群体算法优化双聚类。Carlos等［7］采用基因和实验条件组表示双聚类编码，提出了一种改进的多目标遗传双聚类算法。

近年，Karaboga［8］提出了人工蜂群算法，该算法模拟蜜蜂采蜜行为随机搜索优化，具有寻优精度高、全局搜索能力强等特点，被广泛应用于求解组合优化以及各类工程问题的优化。离散人工蜂群算法被提出应用于离散优化工程问题，比较常用的离散方法有SF（Sigmoid Function）方法［9］，二进制粒子群算法［10］、离散人工蜂群算法［11］均采用SF方法。朱冰莲等［12］提出了一种基于逻辑运算的人工蜂群算法，解决了离散人工蜂群算法策略更新问题，有效提高了离散优化的性能，加快了算法的收敛速度。

本文在离散人工蜂群算法的框架下，提出了基于逻辑运算的离散人工蜂群优化双聚类算法（LOABCB算法）。该算法提高了双聚类的全局寻优能力，能发现基因表达数据中一个或多个具有生物意义的全局最优双聚类。

2 双聚类

2.1 双聚类模型

令基因表达数据矩阵为Am×n，其中矩阵A中的行集合为基因集合G={g1,g2,…,gm}，列集合为实验条件集合C={c1,c2,…,cn}，aij为表达矩阵Am×n的元素值，代表在第j列实验条件下第i行基因的表达值。

AI×J为双聚类，其中I为基因集合的子集I⊆G，J为实验条件集合的子集J⊆C，在理想状态下，双聚类的元素值aij可以定义为行均值加上列均值减去矩阵均值（1）。然而，基因数据中存在噪声，双聚类并不一定是理想的，因此定义残差值表达元素与双聚类其他元素表达的标准。元素值aij的残差值定义为式（2）。

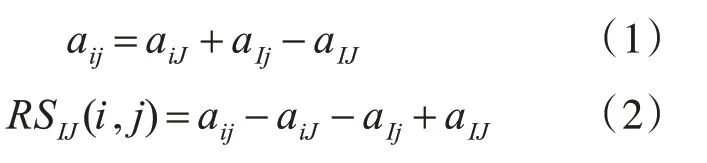
元素值aij的残差值越小，表示aij与双聚类其他元素的相互表达一致性越大。因此，均方残值是衡量双聚类基因和实验条件相关性的重要指标。均方残值的表示为H(I,J)，定义为式（3）。

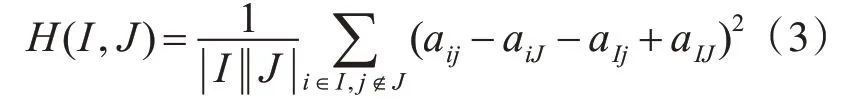
如果满足H(I,J)≤δ，且δ≥0，则子矩阵AIJ叫做δ-双聚类。

2.2 双聚类基因差异表达

优化具有生物意义的双聚类是选择相互表达的相似基因，如图1所示，gt为初始基因，g1～g4为优化产生的基因，其中，基因g1～g3表达模式与初始基因gt表达模式较一致，基因g4的表达模式有较高的差异度。

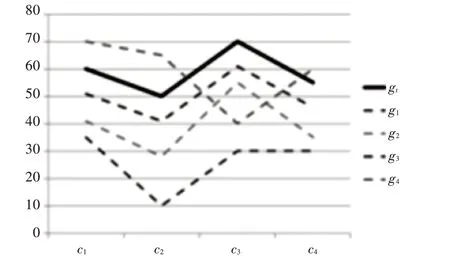
图1 基因表达图谱

对双聚类矩阵Am×n进行基因表达模式转换，保持行基因m不变，列为实验条件集合两两组合n(n-1)/2，产生变换矩阵Bm×n(n-1)/2，矩阵B变换规则如式（4）。

其中，i∈[1…m]，j∈[1…n(n-1)/2]，p＜q。

表达差异度的确定公式如式（5）：

式中，Bt为目标向量，Bi(t≠i) 为比较向量，COMPARE是Bt和Bi的比较操作符，di记录比较操作在某一列的返回值，相同返回0不同则返回1。表达差异比率计算公式如式（6）：

式中，ε为表达差异比率，表示di中1的比率，其中，D=n(n-1)/2。

3 人工蜂群算法

人工蜂群算法（Artificial Bee Colony，ABC）是建立在群体性智能和蜂群高度社会化的一种随机搜索优化算法。人工蜂群算法分为三类群体，根据蜜蜂的分工协作分成雇佣蜂、跟随蜂和侦察蜂。雇佣蜂负责搜索蜜源记录相关信息，按照一定的概率分享将蜜源信息传递给跟随蜂。跟随蜂主要任务为开采蜜源，挑选高质量蜜源进一步进行领域搜索。侦察蜂是一只虚拟蜂，具有全局随机搜索引导作用。当雇佣蜂和跟随蜂多次搜索仍未获得较高质量的蜜源时，雇佣蜂转变为侦察蜂重新随机寻找新的蜜源。

假定蜜蜂种群的规模为N，蜜源、雇佣蜂、跟随蜂的数量均为N。在一个D维空间里，Xi表示第i个食物的当前位置，如式（7）所示。

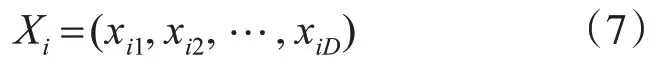
雇佣蜂的初始位置从D维参数中随机产生，由式（8）产生：

其中，i∈{1,2,...,N},j∈{1,2,...,D}，ub和lb分别表示搜索空间的上限与下限的范围值。

ABC算法中，雇佣蜂根据式（9）从D维空间中随机抽取一个维度进行更新。

其中，k∈{1,2,...,N}-{i}，φi,j=rand[-1,1]为[-1,1]上的随机数。xk,j表示第k只雇佣蜂第j维上的分量。

雇佣蜂进行邻域搜索、适应度评价、蜜源位置更新后，产生较优蜜源并传递给跟随蜂。跟随蜂按照一定的概率式（10）选择蜜源，然后根据雇佣蜂邻域搜索式（9）进行位置更新。

其中，me为雇佣蜂的数量，fiti表示第i个蜜源的适用度，pi表示第i个蜜源被选中的概率。

当雇佣蜂和跟随蜂的搜索达到最大限制次数limit，表示当前蜜源质量未得到提升，则雇佣蜂转为侦察蜂，根据式（8）进行重新搜索，最后获得全局最优解。

4 基于逻辑运算的离散人工蜂群双聚类算法

4.1 编码方式

将离散人工蜂群算法应用到双聚类搜索中，首先对双聚类进行编码。双聚类为一个长度为1*(m+n) 固定数组，解的形式为Xi={xi1,xi2,…,xi,m+n}，其中m和n分别表示基因表达数据矩阵的基因数和实验条件数。Xi∈{0,1}即解X的值非0即1，当解xij=1，j∈{1,2,…,m+n}，表示对应j位可选，对应的基因或实验条件属于该双聚类；当解xij=0则表示第j位不可选，不包括在双聚类中。

4.2 邻域搜索策略

人工蜂群算法邻域搜索过程主要集中在侦察蜂和跟随蜂两个阶段，即侦察蜂和跟随蜂在D维空间中进行单维度更新，离散人工蜂群算法解Xi在D维空间的值非0即1，由于新解的产生仅仅为简单的取反运算，这种随机性操作导致大量劣质双聚类出现。

针对离散二进制优化问题，既要保证新解与原解的差异，又要考虑双聚类的优化程度。采用海明距离表示各个解向量之间的差异度［13］建立群体间的学习模型，通过表达差异比率平衡更新策略，加快优质双聚类产生，策略如下：

设置交叉比率R，按照比率随机抽取D维空间维度值更新，更新公式如式（11）：

式中，i≠k，“⊕”表示解向量在D维空间对应维间的异或操作。

设置表达差异比率阈值th，当xij=1且εij≥th，进行解的变异更新如式（12）；否则保持原解不变。

在邻域搜索过程中，Xi为当前解，表示为Xi={xi1,xi2,…,xiD}，Xk为种群中随机挑选出的邻域解，表示为Xk={xk1,xk2,…,xkD}。式（11）通过当前解和邻域异或操作更新单个维度上的值产生新解，式（12）根据表达差异比率对当前解进行取反操作，产生新解。

4.3 算法步骤

LOABCB算法步骤：

5 实验结果及性能分析

基于逻辑运算的离散人工蜂群优化双聚类算法实现环境为Windows 8.1，PC机为2.5GHz CPU Intel Core（TM）i7-4710MQ 12GB内存，采用Matlab 2012b编程。实验数据采用酵母细胞基因表达数据集，该数据集为CC算法使用的基因表达数据集。基因表达数据集经过处理后可以减少噪声的影响，提高双聚类的生成质量，数据网址为http：//arep.med.harvard.edu/biclustering。

5.1 实验数据描述

酵母细胞基因表达数据集采用Tavazoie等［14］的生物实验，包含2884个基因17种实验条件下的表达数据。Cheng和Church［1］对原始酵母细胞基因表达数据集进行预处理，缺失值用-1替换，其余值取对数后乘于100，使得表达数据的取值范围在［0，600］。

5.2 性能分析

5.2.1 实验结果比较

为了验证LOABCB算法的有效性，本文选择了近年来新提出的几个优化算法进行比较，包括多目标进化算法以及在多目标进化算法基础上进行改进的双聚类算法SPEA2B［5］、eMOGB［7］，MOPSOB［6］，OMOACOB［6］，MOSFLB［16］，以及采用人工蜂群双聚类的MOABCB［17］算法。

本文LOABCB算法参数设置与其他比较算法参数设置如表1所示，其余参数表达差异比率阈值th为0.3，最大迭代次数MCN为100，蜜源停留最大限制次数limit为10。

表1 酵母细胞基因表达数据集参数设置

从表2中可以看出，在酵母细胞基因表达数据集的实验结果中，本文算法获得的双聚类平均均方残值优于SPEA2B、eMOGB、MOABCB算法，但平均行数最低，主要原因是算法进行了表达差异比率的双聚类修正，降低了平均均方残值和平均行数。对比于其它比较算法，LOABCB算法获得的双聚类平均列数高于其他比较算法，说明LOABCB算法具备最优解优化的性能。

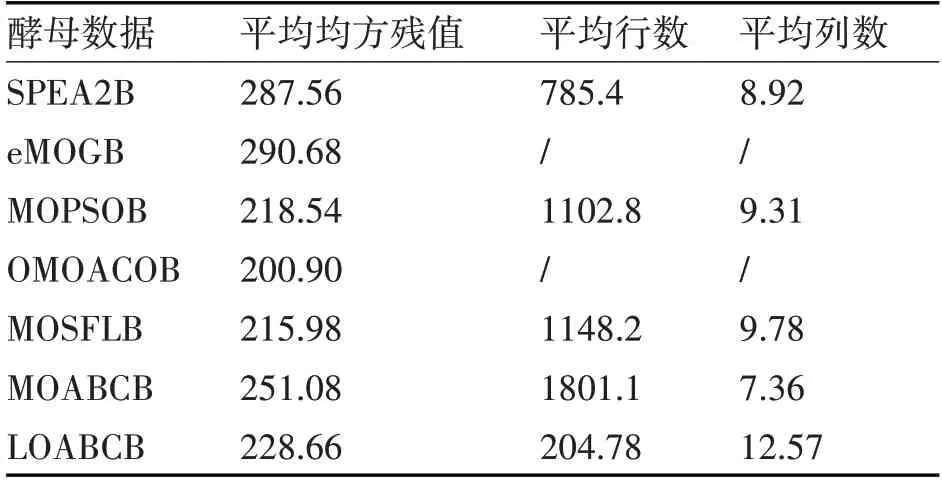
表2 酵母细胞基因表达数据集结果比较

5.2.2 生物注释富集比较

基因本体（Gene Ontology，GO）是目前应用最广泛的基因注释体系之一，描述了基因产物相关的生物过程、细胞组成和分子功能。它是生物学中极为重要的方法和工具，基因表达数据双聚类是挖掘具有某种生物学上意义的问题，为了验证本文算法获得的双聚类参与了生物过程，首先通过计算P-value评价双聚类的统计相关性，然后用GO功能进行评价衡量基因集合的富集程度。

实验采用在线工具FuncAssociate［18］（http：//llama.mshri.on.ca/funcassociate）计算P-value评价算法的统计相关性，当P-value小于5%时说明基因在对应GO上出现富集。如图2所示，本文算法与CC［1］、ISA［19］、OPSM［20］、MBA［21］分别取P-value=5%、1%、0.5%、0.1%和0.001%进行比较。本文算法获得的双聚类P-value为5%比例高于CC和ISA算法，低于OPSM和MBA算法。双聚类P-value为0.001%比例高于CC、ISA、OPSM算法仅低于MBA算法。

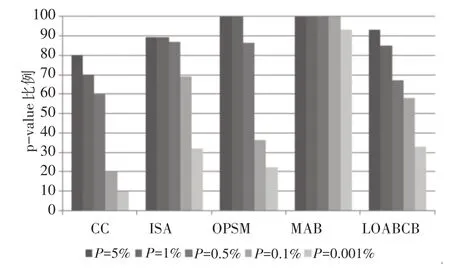
图2 双聚类GO富集注释比例

表3 双聚类Bicluster10的GO富集注释

实验采用FuncAssociate工具对每个双聚类计算P-value，评价双聚类中基因与对应GO注释富集的匹配程度。表3表示双聚类Bicluster10中P-value小于5%时的GO注释富集详细情况，共富集了16个GO功能类别，其中最显著富集注释是P-value小于0.001的属性“chromosome organization”，对应的基因本体ID为GO：0051276。结果表明LOABCB算法所得结果具有富集注释的多样性，可以挖掘出具有显著性富集注释功能的生物信息。

综上所述，本文提出的算法LOABCB发现的双聚类具有较高的质量，能够在离散人工蜂群优化的框架下维持最优解的多样性，同时具备生物学意义的双聚类。

6 结语

本文在离散人工蜂群优化算法基础上提出了一种基于逻辑运算的全局调控基因表达模式的双聚类算法（LOABCB算法）。算法采用邻域搜索策略不断更新蜂群搜索位置，在优化过程中采用均方残值度量蜂群之间的优劣，通过基因表达差异比率对双聚类进行修正。实验表明，LOABCB算法能够在离散人工蜂群优化的框架下通过邻域搜索策略更新解，维持最优解的多样性产生具有高相关表达的双聚类。此外，与其他算法相比，本文算法所得双聚类具有高显著的基因GO富集注释，从而表明LOABCB算法的多样性、有效性和生物意义。