隐蔽空间下超宽带 TDOA定位算法研究

王佰亮，刘江波

(国家粮食和物资储备局，北京 100038)

1 概述

随着国内城市化和机动化的加快，具有节能、快捷和大运量特征的城市轨道交通建设越来越受到众多城市的关注，轨道交通路网建设进程不断发展。其中，施工安全是整个轨道交通建设行业的重要问题，特别是隧道等隐蔽空间施工安全问题。隐蔽空间施工环境艰苦恶劣、危险系数高、施工人员多，使得施工建设企业面临巨大的管理难度。因此，通过新型技术手段实现对隐蔽空间工作人员的准确定位，对保障人员安全、灾后急救等尤为重要。

尽管GPS 可以很好的解决室外多数环境中的精确定位问题，但对于各种室内、地下、隧道等特殊场景，GPS 却无能为力。目前，应用于各种室内、地下、隧道等特殊场景的主流定位技术包括Wi-Fi定位技术、射频识别技术、Zigbee 定位技术、UWB 定位技术等[1]。UWB 定位技术由于定位精度高[2-3]，部署方便，在隐蔽空间定位中得到了广泛的应用。各种定位系统中常用的位置解算方法有最小二乘算法、泰勒级数算法、Chan 算法等[4]。这些算法应用于隐蔽空间定位的不足之处在于：LS 算法虽然运算简单快速，但求出的却是次优解；Taylor算法需要一个与实际位置接近的初始值，若初始值误差大将导致算法不收敛，并且Taylor 算法运算量较大[5]；Chan 算法和LS 一样，虽然计算快捷，但是在非视距(NLOS) 环境下定位性能显著下降[6]。BP 神经网络有强大非线性映射能力，近年来广泛运用于各种定位系统，在提高定位精度上有较大的优势[7-9]，但也存在收敛速度的问题。为此，研究了一种结合最小二乘位置求解方法（LS）的BP 神经网络定位算法，在提高BP 收敛速度的同时提高定位精度。

2 最小二乘融合BP神经网络定位算法

2.1 融合定位思路

最小二乘融合BP 神经网络定位算法的基本思路是：利用测量得到的TDOA 值和已知的基站坐标，采用LS 算法进行位置计算，获得一个与实际位置接近的待测节点位置的粗估计；然后根据待测节点初始估计位置坐标及基站坐标，进行TDOA 测量值重构；运用重构TDOA 及基站信息进行BP 神经网络训练及位置解算，优化LS 计算结果，从而获得最终定位结果。具体过程如图1 所示。

2.2 最小二乘位置估计算法

假设参与定位的基站坐标为,待测节点坐标为(xi，yi)，i=1，2...N。基站与待测节点间的距离用(x，y)来表示。则：

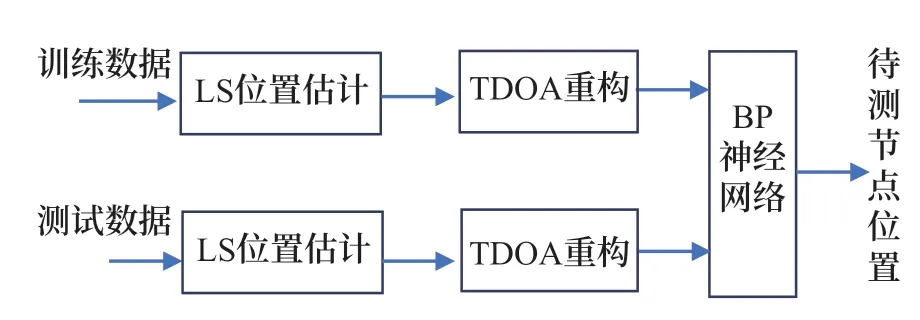
图1 最小二乘融合BP神经网络定位思路Fig.1 The scheme combing least square and BP neural network

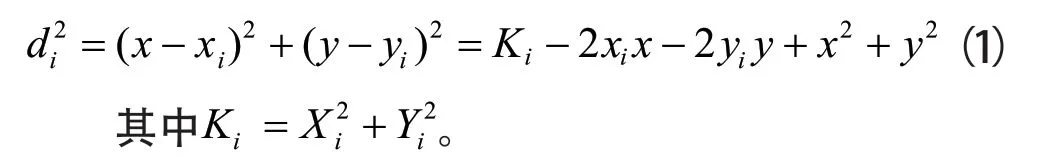
令di，1表示待测节点到基站i与基站1 的距离差。则

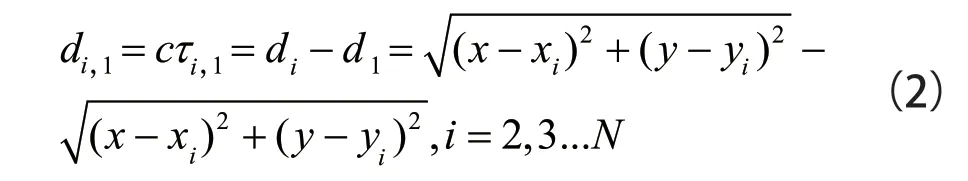
其中c为电波传播速度，τi，1为TDOA 测量值。对该非线性方程组进行线性化处理，得到

式中xi，1=xi-x1，yi，1=yi-y1。

将x，y，d1看成未知数，公式（4）写成矩阵的形式为

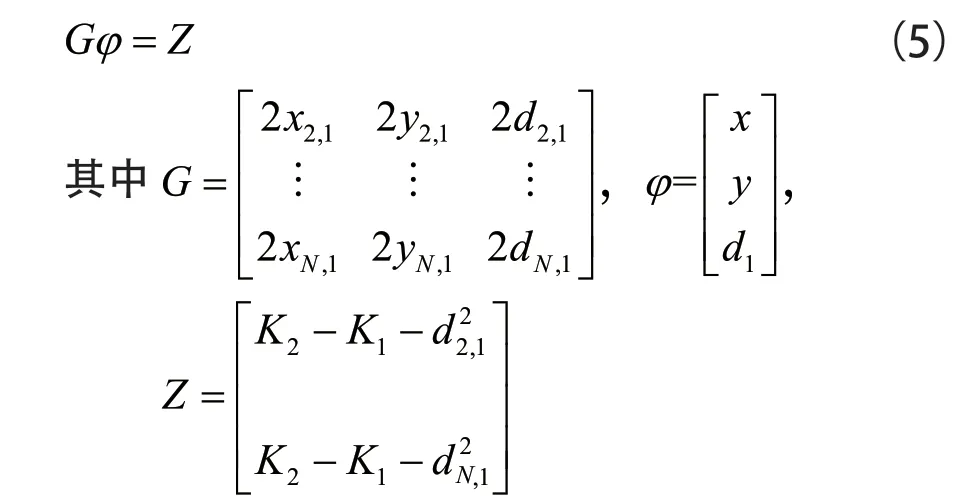
利用最小二乘法求解（5）式得

其中x,y即为待测节点估计位置。利用该估计结果，根据公式（2）即可进行TDOA 重构。

2.3 BP神经网络位置解算原理

BP 神经网络位置解算利用重构TDOA 进行网络训练，训练好的网络将用于对测试数据的位置解算。一般来说，BP 神经网络是一个多层网络，包括输入层、输出层和隐含层，其中隐含层可以为一层或多层。由于定位模型复杂度不高，经过实测数据进行验证分析，选取单隐层BP 神经网络对待测节点进行位置估计，其结构如图2 所示。

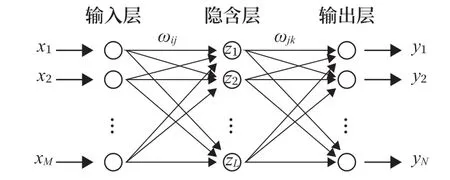
图2 BP神经网络结构Fig.2 Structure of BP neural network

BP 神经网络输入层由M个神经元构成，M的个数由参与定位的基站数决定。输入层的输入是参与定位的基站坐标及重构TDOA，即该TDOA 由LS 算法定位结果修正得到。输入层的数据结构如表1所示。

输出层由N（N=2）个神经元构成，对应估计得到的待测节点坐标（x,y）。

隐藏层含有L(L=11)个神经元。隐含层神经元的激活函数选取为tansig 函数，公式为

表1 输入层数据结构Tab.1 Data structure of input layer

则隐含层的输出为

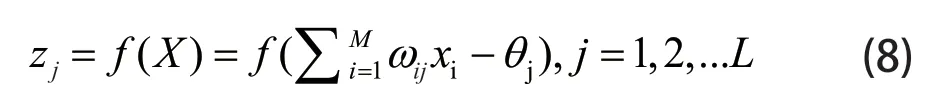
输出层的激活函数选取为线性purelin 函数。则输出层的输出为

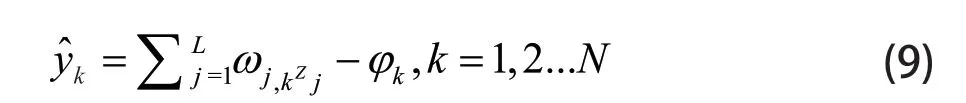
定义误差输出函数为

利用反向传播训练函数trainlm 函数进行权值更新，更新过程中学习率选取为0.01。

3 性能仿真分析

仿真区域设置为边长10 m 的二维正方形平面区域。在该区域布置5 个基站，坐标分别为：（0，0）,（0，10），（10，0），（10，10），（5，5）。待测节点在二维平面区域内随机分布，测量误差服从高斯分布，非视距误差服从高斯分布或指数分布。具体仿真过程如图3 所示。

图3 仿真过程Fig.3 Process of simulation

基站与待测节点间视距传输时的仿真结果如图4、5 所示。视距传输时只考虑测量误差。从图4、5 中可以看出测量误差分别服从均值为0，标准差为10 cm 或15 cm 的高斯分布。基站与待测节点间非视距传输时的仿真结果如图6、7 所示。非视距传输时除考虑测量误差外还要考虑非视距误差。从图6、7 中可以看出测量误差都服从均值为0，标准差为10 cm 的高斯分布；如图6 所示非视距传播的误差服从均值为50 cm，标准差为10 cm 的高斯分布。如图7 所示非视距传播的误差服从指数分布，指数分布的均值为tm，tm=Tdαω，其中10 lg(ω)～N(0，σω)，σω=4，T=19 ns，α=0.5。

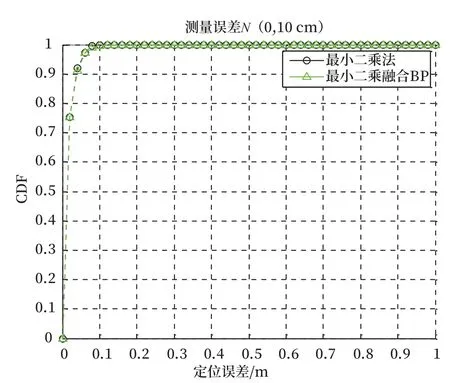
图4 视距-测量误差N(0,10 cm)定位误差Fig.4 LOS-the positioning accuracy for measurement error of N (0,10 cm)

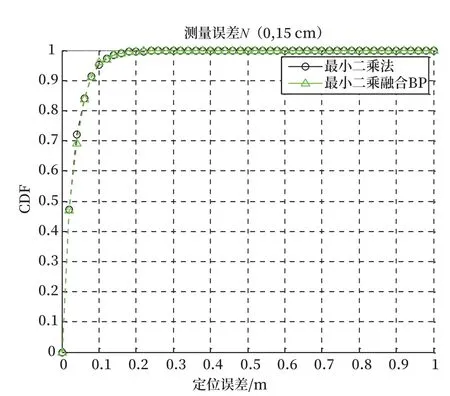
图5 视距-测量误差N(0,15 cm)定位误差Fig.5 LOS-the positioning accuracy for measurement error of N (0,15 cm)

图6 非视距-NLOS N(50 cm,10 cm)定位误差Fig.6 NLOS-the positioning accuracy for NLOS N (50 cm,10 cm)

对比最小二乘融合BP 神经网络的定位方案以及最小二乘法定位方法的定位误差累积分布函数可知，在视距传输情况下，最小二乘融合BP 神经网络的定位方案与最小二乘法定位方法定位精度相当。但在非视距环境下，最小二乘融合BP 神经网络的定位方案定位精度明显高于最小二乘法定位算法。在非视距误差服从均值为50 cm，标准差为10 cm的情况下，最小二乘融合BP 神经网络的定位方案中定位误差小于20 cm 的概率接近80%；而最小二乘法算法定位误差小于20 cm 的概率只有大概20%。在非视距误差服从指数分布的情况下，最小二乘融合BP 神经网络的定位方案中定位误差小于20 cm 的概率接近100%；而最小二乘法算法定位误差小于20 cm 的概率只有大概22%。

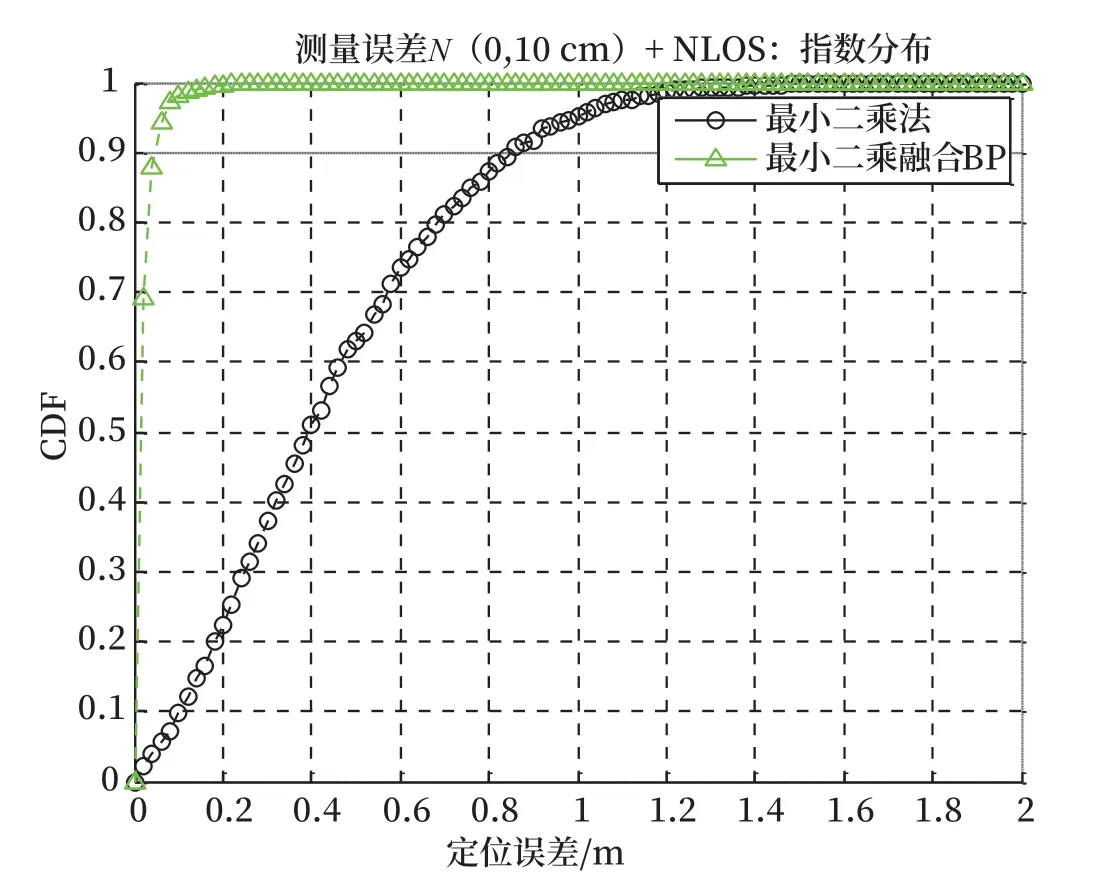
图7 非视距-NLOS指数分布定位误差Fig.7 NLOS-the positioning accuracy for exponential distribution of NLOS

其次，4 种情况下各算法的定位误差最大最小值及均方根误差如表2 所示。

从表2 可得到和图4～7 相似的结论。同时可以看出，在非视距情况下，最小二乘融合BP 神经网络的定位方案中定位误差均方值远远小于最小二乘算法。

4 结束语

研究一种基于TDOA 的最小二乘和BP 神经网络融合定位算法，该算法在NLOS 环境下利用BP神经网络进行最小二乘法定位结果优化，降低了NLOS 误差的影响，明显提高了定位精度。实验结果表明，该算法在非视距情况下定位性能远优于最小二乘法，具有较强的抗 NLOS 误差能力，能适应不同环境下定位的需求。

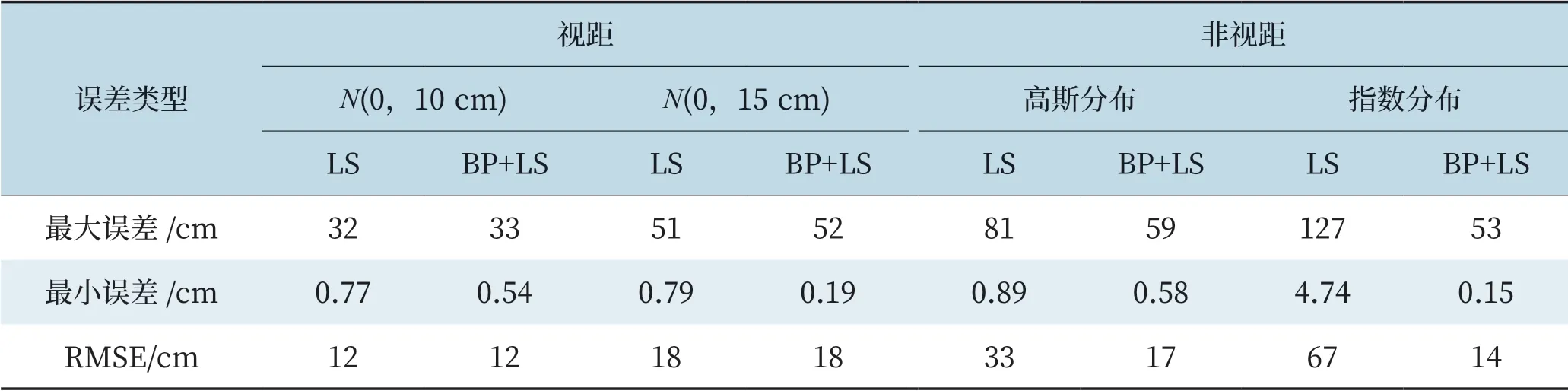
表2 均方根误差Tab.2 Root mean square error