一种描述列车运行轨迹的时间-速度-位置模型

江 明

(1.北京全路通信信号研究设计院集团有限公司，北京 100070；2.北京市高速铁路运行控制系统工程技术研究中心，北京 100070)

1 概述

铁路在组织旅客和货物运输的生产过程中，列车运行是一个很复杂的环节，它要利用多种铁路技术设备，要求各个部门、各工种、各项作业之间互相协调配合，才能保证行车安全和提高运输效率。为了描述列车运行状态，调度指挥系统的核心是采用时间-位置模型的列车运行图，列车运行控制系统的核心是采用位置-速度模型的控车曲线。时间-位置模型和位置-速度模型均部分反映了列车运行状态，但同时也忽略了一些状态，因而无法反映列车运行状态的全貌。

列车运行图是用以表示列车在铁路区间运行及在车站到发或通过时刻的技术文件，是列车运行时空过程的图解，运用坐标原理对列车运行时间、空间关系进行表示[1]。列车运行图采用时间-位置模型，能清晰地展示各类列车计划占用区间的顺序、列车运行经过的交路（含起始站、终到站和所有中间站）、列车在各车站到发或通过的时刻、在车站的停站时间、在终点站的折返作业时长等内容[2]。但是，列车运行图未考虑列车实际运行速度和车长因素，未考虑各种不同类型的线路限速，也未考虑列车故障带来的影响，无法反映列车实际运行状态。当由于自然灾害、基础设施、人为因素等导致列车晚点，造成列车实际运行偏离计划时，当前列车运行图提供的信息无法满足快速准确的列车运行调整需求。

列车运行控制是保证行车安全的关键因素，主要通过控制列车运行速度来保证列车间的安全行车间距，保障列车的安全运行。列控车载控车曲线采用位置-速度模型，考虑了列车实际运行速度、各种不同类型的线路限速以及车长因素，但是未考虑时间因素、列车故障带来的影响，也未考虑列车内不同车厢之间的关系，提供的信息也无法满足快速准确的列车运行调整需求。

为了在一个统一的模型中整体描述列车运行的精确过程，综合列车运行图的时间-位置模型、列车运行控制的位置-速度模型两个模型的优点，本文提出一种综合考虑时间-速度-位置3 个维度的模型（TVP 模型），能够描述包含时间、列车速度、列车位置等丰富信息的列车运行状态。结合列车多质点模型，将列车分解为多个列车质点，在此基础上分析了列车质点在时间-速度-位置三维空间中相关的安全区域、可达区域、协同区域等区域的边界及其特点，给出了列车安全可达区域的范围。最后，从运输组织、调度指挥、运行控制、控制调度一体化等多个方面总结梳理了该模型适用的应用领域。

2 时间-速度-位置模型

时间-速度-位置模型描述了一个由时间、速度、位置3 个维度构成的列车运行区域，定义了包括安全区域、可达区域、协同区域、安全可达区域在内的一系列区域。将列车分解为多个列车质点，三维空间中的每个点代表一个列车质点的运行状态，一条线代表一个列车质点的运行轨迹，一簇线代表列车的运行轨迹。TVP 模型综合考虑了线路条件、各种不同类型的线路限速、列车故障、列车实际运行速度、车长、列车内部车厢间关系等因素对列车运行的影响，能够更为精确地描述列车运行状态和运行轨迹。

列车运行区域TRA，是一个由指定的运行时间段T=[T0,T1]、线路设计速度V=[0,V设]、指定的线路范围P=[P0,P1]确定的三维区域。其中T可按实际需要选取，如3 h、24 h、一个月等；P可按实际需要选取，如调度台管辖范围、线路管辖范围、路局管辖范围等。为了更好地描述TVP 模型，本文后续均以一站一区间10 km 长度的线路作为示例，考虑1 000 s 的时间长度，线路设计速度为250 km/h，线路平面如图1 所示。对应的列车运行区域如图2 所示，其中T=[0,1 000]（s）、V=[0,250]（km/h）、P=[0,1 000]（10 m）。

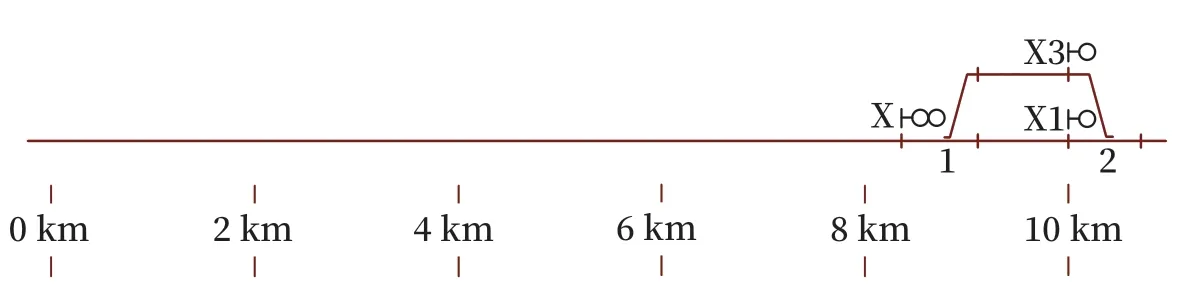
图1 示例线路平面图Fig.1 Layout of the example line

在本模型中，待描述的列车可采用各种不同的车型，既可以是动车组，也可以是机车。采用多质点模型[3]，把列车看成是多个质点连接成的“质点链”。假定一列列车由若干个列车质点构成，每个列车质点i在时刻t具有一个唯一的运行状态，可用三维空间中的一个点（t,vi(t),pi(t)）来描述。其中，vi(t)指的是列车质点i在时刻t的运行速度，pi(t)指的是列车质点i在时刻t的运行位置。图2 中给出几个列车运行状态的示例。其中，红色列车表示一列8 节编组的动车组，图中给出不同时间不同位置的两个状态，每个“*”代表一个列车质点；蓝色列车表示一列20 节编组的机车牵引列车，图中给出了不同时间不同位置的两个状态，每个“〇”代表一个列车质点。由于机车牵引列车采用车钩来连接不同车厢，在运行过程中可能存在不同列车质点速度不同的运行状态。该状态在列车运行图的时间-位置模型、列车运行控制的位置-速度模型中都无法描述，而本模型可精确描述同一列车不同列车质点在同一时刻的不同速度，如图2 所示。

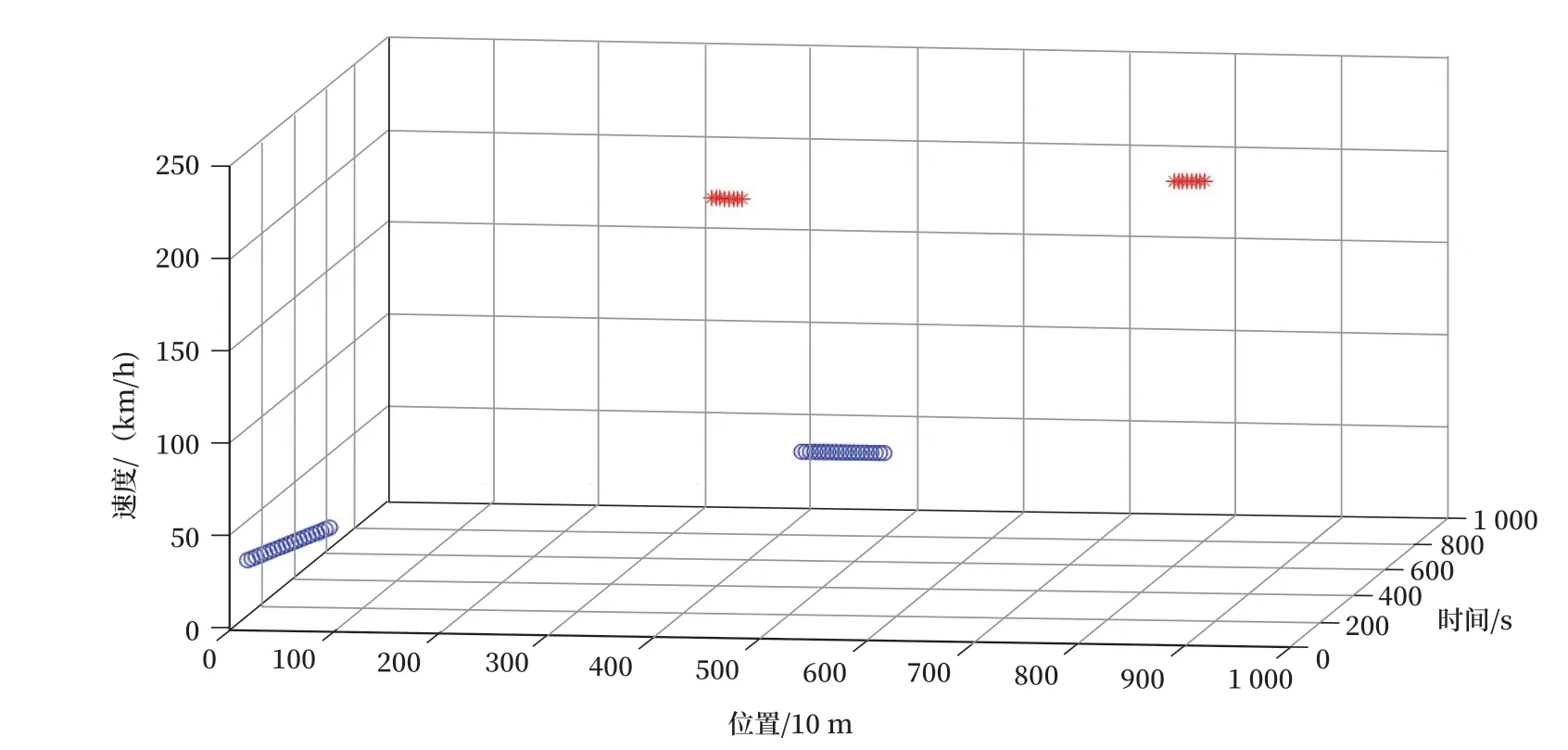
图2 列车运行区域及列车运行状态示例Fig.2 Example of train running area and train running status

将不同时刻列车质点的运行状态顺序相连，即可获得列车质点的运行轨迹。构成列车的列车质点运行轨迹的综合，即为列车的运行轨迹。

3 时间-速度-位置模型的特性分析

3.1 列车质点安全区域

一个列车质点i的安全区域SA（i），是指在列车运行区域内，仅考虑单个列车质点i、不考虑其他列车质点的前提下，由所有表示列车质点i运行处于安全状态的点组成的区域，即列车质点不超速的区域。由于每列车的动力学特性不同，不同列车质点的安全区域有可能不同，且该区域是一个随着时间不断变化的区域。

为描述安全区域的示例，在图1 所示线路上增加其余假定条件：车站接近区段（7～9 km）的允许速度为200 km/h；在700～1 000 s、0～2 km 范围内设置速度为120 km/h 的临时限速；在0～100 s 范围内设置100 s 的天窗；车站进站信号机X 于时刻为500 s 时开放，1 号道岔开通道岔侧向，道岔限速80 km/h。

根据导致列车质点非安全状态的原因，可将非安全区域分为3 种，分别是线路条件导致的非安全区域NSA1、因外部环境导致的非安全区域NSA2、因列车自身运行导致的非安全区域NSA3。从列车运行区域去掉非安全区域，剩余的区域即为列车质点的安全区域。

线路条件相关的非安全区域NSA1 指列车质点速度超过各种静态限速的区域。在示例中，车站接近区段（7～9 km）的允许速度为200 km/h，低于线路设计速度，构成非安全区域NSA1。该区域是一个时不变的区域，仅在固定地段存在，与时间无关，与列车运行图的排列无关，与列车特性无关，如图3 中绿色区域所示。

外部环境相关的非安全区域NSA2 指风雨雪、异物入侵等环境条件导致的列车允许速度下降。在示例中，因环境因素导致在700～1 000 s、0～2 km范围内设置了速度为120 km/h 的临时限速，构成非安全区域NSA2。该区域是一个时变的区域，仅在某一时段某一区段存在，与列车运行图的排列无关，与列车特性无关，如图3 中红色区域所示。

图3 列车质点安全区域与非安全区域示例图Fig.3 Schematic diagram of safe and unsafe areas for train particles

列车运行相关的非安全区域NSA3 指与列车质点运行相关的允许速度下降或者禁止列车移动。导致的原因包括天窗对应区域、车辆原因（列车限制速度、列车故障限速）导致的限速、跟道岔相关的限速等。在本示例中，在0～100 s 范围内设置100 s 的天窗；车站进站信号机X 于时刻500 s 时开放，1 号道岔开通道岔侧向，道岔限速80 km/h。这些因素构成非安全区域NSA3（i）。该区域是一个时变的区域，仅在某一时段某一区段存在，与列车运行图的排列有关，与列车特性有关，如图3 中蓝色区域所示。

综上可知，列车质点i对应的安全区域为SA（i）=TRA-NSA1-NSA2-NSA3（i），其中SA、NSA3 与i相关，TRA、NSA1、NSA2 与i无关。见图3 中灰色区域。

3.2 列车质点可达区域

对于列车质点i，指定列车运行区域中的任意两个点E0(i)=（t0,vi(t0),pi(t0)）、E1(i)=（t1,vi(t1),pi(t1)），如果根据线路坡度、曲率等参数以及列车质点i的动力学参数，能够找到至少一条从E0(i)到E1(i)的运行轨迹，则称从E0(i)到E1(i)的关系为可达，其中E0(i)为可达关系的起点，E1(i)为可达关系的终点。

对于列车质点i，以Et(i)=（t,vi(t),pi(t)）为起点或终点，所有具有可达关系的点组成的区域称为可达区域RA（i）。影响可达区域大小的因素包括：线路坡度、曲率，列车质点的质量、牵引制动参数、黏着系数等。从定义可知，可达区域分为两种：一种是以该点作为起始点，能够达到的所有终点组成的可达区域RA1（i）；一种是以该点作为终点，满足可达条件对应的所有起点组成的可达区域RA2（i）。

该区域仅与列车质点所在位置的线路条件以及列车质点的特性有关，是一个时不变的区域，与列车运行图的排列无关。

3.3 列车质点协同区域

当一列车需要用多个列车质点来描述时，除了所有的列车质点均处于安全区域内，还需要列车质点间不存在冲撞、挤钩、断钩等风险，方可表示整列车的运行处于安全状态。因此，为了保证列车运行安全，还需要考虑因列车质点间的交互状态导致的协同区域CA。不同列车构成的列车群也同理，只需将列车质点替换成列车即可。

考虑列车质点i，它与前行列车质点i-1 交互，时刻t时它们在列车运行区域中所处的点分别为Et(i)=（t,vi(t),pi(t)），Et(i-1)=（t,vi-1(t),pi-1(t)）。如果两个列车质点间采用车钩连接，则需避免挤钩、断钩的情况；如果两个列车质点（在列车群的场景下则为两列车）间无车钩连接，则仅需要避免冲撞（含冒进信号）即可。如果对位于Et(i)的列车质点i与位于Et(i-1)的列车质点i-1 满足上述要求，则称其关系为协同。

与处于Et（i）的列车质点i具有协同关系的所有点构成的区域称为协同区域CA（i）。影响该区域大小的因素包括：线路坡度、曲率，列车质点及相邻质点的质量、牵引制动参数、黏着系数等。协同区域也可分为两种，一种是针对车钩连接的场景，在任一时刻t列车质点间位置或速度的差异不至于大到导致挤钩或断钩的区域CA1（i）；另一种是针对无车钩连接的场景，按照列车质点制动性能能够避免列车质点与前行相邻列车质点相撞的区域CA2（i）。根据信号制式的不同，在固定闭塞制式下，CA2（i）还应包括避免冒进信号的区域。

该区域仅与列车质点所在位置的线路条件以及列车质点的特性有关，是一个时不变的区域，与列车运行图的排列无关。

3.4 列车安全可达区域

指定列车运行区域中的任意到站停车点Et=（t,0,p），考虑指定车型（即动力学参数）的列车（含列车质点1…N），则列车质点i对应的安全区域与可达区域的交集即为停车点Et对列车质点i的安全可达区域SRA（i）。

所有列车质点的安全可达区域与所有列车质点的协同区域的交集，为整列车的安全可达区域在此区域内，求解得出的任意一条列车运行轨迹，可确定一条能够满足安全运行条件的列车驾驶策略。

4 时间-速度-位置模型的应用领域

TVP 模型能够比时间-位置模型、速度-位置模型提供更为丰富、更为精确的列车运行状态，在运输组织、调度指挥、运行控制、控制调度一体化等方面均可获得广泛应用。

4.1 运输组织应用领域

TVP 模型可用于列车运行图评估。在本模型中可计算各列车质点的可达区域，当前行列车晚点时，可根据可达区域定量计算前车晚点对后续列车的影响，从而评估列车运行图对故障的容忍能力和恢复能力。

TVP 模型可用于计算运输组织关注的重要参数，包括但不限于：

追踪间隔，在列车运行区域绘制出所有列车的运行轨迹，计算两根相邻列车运行轨迹经过同一位置的时间差，取其最大值即为最小追踪间隔；

线路输送能力，由于采用了多质点模型，在本模型中具备列车辆数、追踪间隔等信息，结合列车重量，即可计算线路输送能力。

4.2 调度指挥应用领域

TVP 模型可用于运行计划调整。当实际运营过程中因受到随机因素干扰导致前行列车偏离计划运行时，通过计算列车的安全可达区域，并从中选取一条最优的列车运行轨迹，可有效指导尽快恢复运输秩序，更好满足快速准确的列车运行调整需求。

TVP 模型可用于异常情况报警。在本模型中，可实时评估列车的实际运行轨迹与安全区域、协同区域的关系。当运行环境发生变化导致安全区域、协同区域变化时，可预测后续列车运行状态，当出现异常情况时向调度员报警。

4.3 运行控制应用领域

TVP 模型可用于列车运行安全性检查。当列车运行轨迹超出安全可达区域时，说明存在安全风险，需要采取安全控制措施。

TVP 模型可用于控制策略优化，实现节能降耗。例如，在列车安全可达区域内选取能耗最优的列车运行轨迹，可实现单车节能降耗。对多车场景而言，在位置维度可细分为若干不同的供电臂，每个切面可表示同一供电臂下运行的列车信息，通过调整该切面内的列车运行，有效利用再生制动能。

4.4 控制调度一体化应用领域

控制与调度一体化的基本理念就是根据铁路运营的需要，以调度指挥的业务流程为导向，深度融合调度指挥和列车运行控制的技术，实现智能、扁平、全局化的控制调度一体化，从而实现路网整体运行效率的全局最优化控制[4]，保障列车群安全高效节能运行，全面提升及时应对突发事件能力。

目前对控制调度一体化的研究已经有初步成果[5]，但是缺乏一个良好的模型来支撑相关研究，制约了一体化研究工作的快速推进。TVP 模型能够同时描述包含列车位置、列车速度以及时间信息的列车运行轨迹，可为控制调度一体化研究提供精确的列车运行状态和列车运行轨迹，为后续研究打下良好基础。和运行轨迹的描述提供一种新的视角和方法论。

5 总结

综合列车运行图的时间-位置模型、列车运行控制的位置-速度模型两种模型的优点，本文提出一种用于描述列车运行状态和运行轨迹的时间-速度-位置模型。结合列车多质点模型，定义列车质点的安全区域、可达区域和协同区域，分析上述区域的边界和特点，给出列车安全可达区域的范围。该模型同时适用于动车组和机车，能够满足运输组织、调度指挥、运行控制、控制调度一体化等多个方面的理论分析和运用实践需求，为列车运行状态