液氮深冷低温箱的数值模拟与实验研究
郭帅帅 杨鹏 贺素艳 赵有信 李金伟 马永志
摘要: 为解决生物样本的深冷低温存储问题,本文设计了一种利用液氮制冷的深冷低温箱,并对低温箱的制冷性能进行研究。采用Fluent软件模拟与实验相结合的方法,模拟低温箱中换热器自然对流换热过程,研究了LN2深冷低温冷藏箱的制冷性能,对自然对流换热时间、低温箱中的气流流动规律以及LN2的消耗量进行预测,结合模拟结果,对低温箱的制冷性能展开实验研究,并将实验数据与模拟数据进行对比。研究结果表明,由于涡流作用,箱体前部温度均匀性优于后部,箱内最大气体流速0.24 m/s,低温箱內平均温度从初始温度288.15 K下降到123 K,耗时264 min,平均制冷量1434.09 kW,该过程消耗LN2质量为 110.94 kg,模拟时间误差16.3%,LN2质量误差15.7%。该研究为LN2深低温冷藏箱的设计提供了理论依据,具有一定的应用价值。
关键词: 液氮; 低温箱; 数值模拟; 制冷性能
中图分类号: TB661; V245.3+43文献标识码: A
作者简介: 郭帅帅(1995-),男,硕士研究生,主要研究方向为制冷技术节能研究。
通信作者: 贺素艳(1967-),女,河北唐山人,博士,副教授,主要研究方向为自复叠制冷研究。 Email: 743702960@qq.com
低温技术是我国国民经济建设和国防现代化过程中不可缺少的技术,通常温度低于173 K以下的冷处理叫做深冷处理,该技术在工业气体液化和分离、材料处理、质检科研、超导应用、航空航天、生物医疗、基因储存、能源以及实验等领域得到了广泛应用[1-3]。液氮(LN2)、液氢及液化天然气等低温液化气体用于深冷处理时,具有简单、清洁、经济等优点,但是其制冷性能的稳定性和制冷效率有待研究。近几年,许多学者对液氮在制冷方面的应用展开了大量研究。徐瀚洲等人[4]设计了一种食品冷藏箱,研究了箱内自然对流和强制对流两种工况下降温的特性和液氮消耗量,结果表明箱内采用风机强制对流的工况下降温更快,但液氮消耗量更大;王斯民等人[5]以LN2作为研究工质,对竖直圆管内低温流体的沸腾相变流动进行了数值模拟,结果表明,冷流体吸热沸腾后,蒸发流成为竖直圆管壁面换热的主要部分,沸腾换热成为主要的换热过程;陈书平等人[6]的研究表明随着LN2流速的增大,气化管内的换热也增加;R. Tavakoli等人[7]提出使用VOF法追踪两相流界面,得到提高计算精度、加快收敛速度的方法,对两相流的模拟计算具有一定的参考价值;M. Herrmann等人[8]建立了基于非结构网格体系上的两相流模型,应用于较精细的网格;Jiang等人[9]采用DNS和LES封闭模型方程建立了单流体两相流模型;V. V. Klimenko等人[10]研究了LN2作为研究工质的强制对流两相流,提出需要气化的冷工质流动方向为从下向上时,传热效果最好。大多数研究者对LN2管内沸腾管热的研究,而关于LN2换热器的自然对流换热的研究较少。基于此,本文采用Fluent软件模拟低温箱中换热器与箱内空气的自然对流换热过程,采用数值模拟与实验相结合的方法,预测自然对流换热时间、低温箱中的气流流动规律以及液氮的消耗量,从而探究深冷低温箱的工作特性。该研究在制冷方面具有一定的应用前景。
1系统介绍
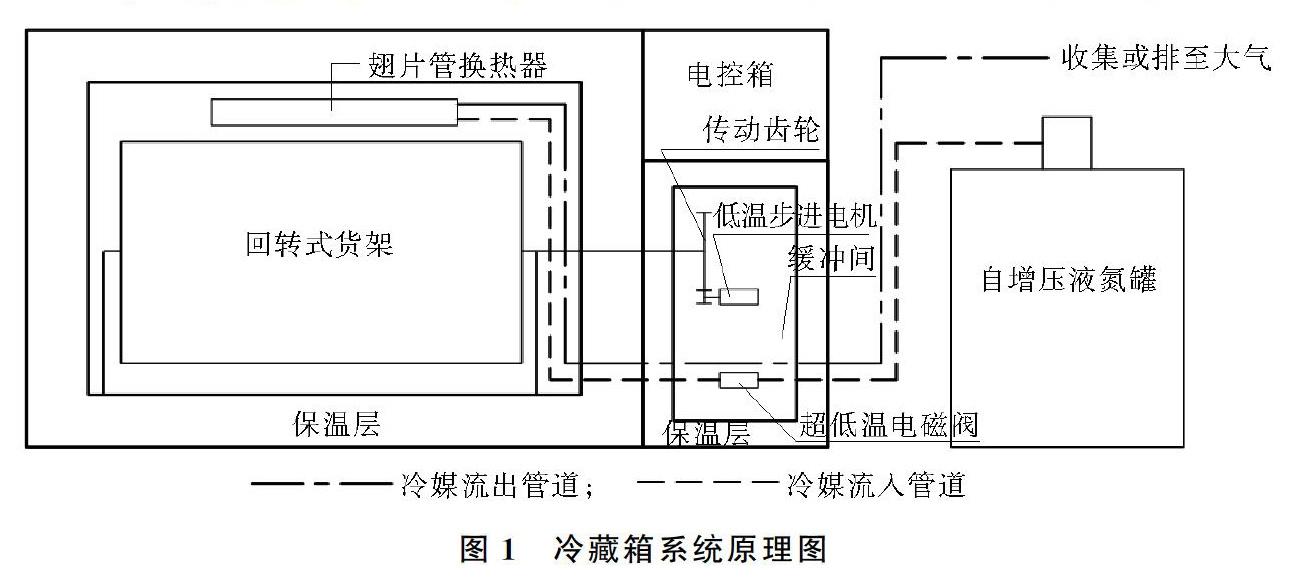
冷藏箱系统原理图如图1所示。该冷藏箱的存储温度设置为123 K,LN2从自增压灌流出,经缓冲间利用下进上出的方式进入翅片管式换热器,换热器在低温箱中通过自然对流的方式进行热交换,使低温箱温度降低。保温层能够减少低温箱内的冷量损失,当低温箱内平均温度低于设定温度时,电控箱发出指令,电磁阀关闭;当低温箱内温度高于设定温度时,电磁阀开启。为观察自然对流过程中低温箱内的温度均匀性及降温速率,对低温箱中自然对流换热过程进行数值模拟,与实验结果进行对比,并检验其合理性。
2低温箱数值模拟研究
2.1几何模型
本文研究的冷藏箱及换热器几何模型如图2所示。图2a中,蓝色区域为低温箱壁,绿色区域为低温换热器部分,低温箱长度为1.9 m,宽度为1.0 m,高度为1.3 m,斜面倾斜度为60°。将换热器简化为与实验中换热器换热面积相同的阶梯型长方体,低温箱外使用保温材料,假设低温箱与外界无热量交换,箱内为干空气,选取LN2为低温介质,不考虑换热器内的相变和箱内辐射换热。初始时刻箱内温度为288.15 K,随着液氮通入换热器,其表面温度开始下降,在自然对流的作用下,箱内温度逐渐下降,直到理想温度。网格划分选用体网格的Tetra/Mixed网格类型,冷藏箱网格划分网格数为196 628,换热器网格划分网格数共为52 623,网格质量检查结果均在0.3以上,质量良好。
2.3计算方法
利用Fluent 16.0软件进行模拟,选用Tecplot360EX 2015R1对数值模拟结果进行处理,求解方法采用压力基求解器,控制方程的离散格式采用一阶迎风格式,速度-压力耦合采用SIMPLE算法进行非稳态计算。当求解器参数设定完成后,设定k-ε标准模型参数,定义重力沿Y轴负方向及计算中管道壁面材料(copper)与冷藏箱壁面材料(aluminum)的属性[14],设定计算边界条件,冷藏箱表面热流为0,由于冷藏箱自然对流传热过程为非稳态过程,换热器壁面平均温度随箱内平均温度发生变化。根据换热器的模拟结果,拟
合出管道壁面温度与环境温度的对应关系,编写成UDF导入Fluent,作为换热器壁面温度设置的依据[1520]。在冷藏箱底部、中部及顶部各设定5个监测点a、b、c、d、e,并设定监测参数。冷藏箱内监测点位置及编号如图3所示。初始化后,patch换热器壁面温度及冷藏箱内部初始温度为288.15 K,设置时间步长、时间步数后进行迭代计算。得到监测点数据后,将监测点a1至e1和a3至e3的数据分别平均后,得到冷藏箱底部和上部平均温度,将监测点a1至e1、a2至e2、a3至e3的数据平均后,得到冷藏箱内平均温度。
2.4计算结果
冷藏箱壁面温度分布云图如图4所示。图4a为自然对流3 600 s时的温度分布云图,最低温度212 K,最高温度216 K,冷藏箱上部温度略高于下部;图4b为换热14 400 s时的温度分布云图,最高温度123 K,最低温度117 K,但温度均匀性更好。
与X轴垂直的冷藏箱中心截面温度分布云图如图5所示,图5a为3 600 s时的温度分布云图,图5b为14 400 s时的温度分布云图。通过模拟结果看出,冷藏箱前部温度高于后部,上部溫度高于下部,换热器周围温度最低,冷藏箱顶面与斜面的交界处温度最高,且换热时间越长,箱内的温度均匀性越好。
冷藏箱底部、中部及顶部平均温度变化曲线如图6。由图6可以看出,降温过程持续262 min,冷藏箱内平均温度由288.15 K下降至116.72 K。在第60 min时,冷藏箱内平均温度为203.40 K;第240 min时,冷藏箱内平均温度为120.90 K;6.4 min时,冷藏箱底部平均温度与顶部平均温度温差最大为11.00 K;67.2 min时,温差降至5.00 K以下,降温过程平均温差为3.89 K。
冷藏箱模拟结果与X轴垂直的冷藏箱中心截面速度分布云图如图7所示。图7a为3 600 s时的速度分布云图,图7b为14 400 s时的速度分布云图。通过模拟可以得出,由于重力作用,在靠近换热器壁面处,低温空气垂直下落至冷藏箱底部后散开,在冷藏箱内部形成涡流,越靠近冷藏箱后壁,空气流速越快,流速随着冷藏箱内温度的降低而减慢,处于0.10~0.24 m/s之间。由于涡流的作用,使与X轴垂直的中心界面上,冷藏箱壁面温度沿顺时针方向逐渐升高。冷藏箱自然对流传热温度均匀性好且过程安全,但降温过程缓慢,需要4.0 h可使冷藏箱最高温度低于设定温度。
3实验研究
3.1实验过程
在进行实验前,首先检查冷藏箱及液氮罐,确保其压力正常,PT100温度探头布置如图8。图中探头a位于换热器管道入口处;探头b位于换热器管道出口处;探头c位于冷藏箱内底部,探头d位于冷藏箱内顶部;探头e位于缓冲间中心处。具体实验步骤为:开启冷藏箱上位机操作系统及液氮罐的自增压阀门,观察液氮罐压力表,当压力升高至0.05~0.09 MPa时,关闭液氮罐的自增压阀门,开启液氮罐的进、排液阀,通过上位机操作系统开启电磁阀,并控制步进电机是否旋转,记录PT100温度传感器显示数据,使用毕托管与倾斜式微压计测量出口处N2流速并记录,调整液氮罐的进、排液阀开度,通过上位机操作系统开启或关闭电磁阀,关闭液氮罐的进、排液阀,通过上位机操作系统关闭电磁阀,关闭冷藏箱上位机操作系统。
复测试根据实验不同要求,调整液氮罐的进、排液阀开度,控制电磁阀开启或关闭,控制步进电机是否旋转,重复以上步骤。实验过程中环境温度为288 K,使用YDZ-200型自增压液氮罐,容器配有升压系统,通过汽化罐内少量LN2使容器内产生压力并连续排液。实验过程中,自增压液氮罐压力表示数保持在0.1~0.2 MPa,符合液氮罐排液压力需求。由于未选用自增压液氮罐专用高精度出口流量控制设备,因此实验过程中液氮罐排液量非恒定值,误差约为±0.1 kg/min。为避免低温窒息等危害,使用一根外径为28 mm的管道,连接冷藏箱与大气环境,并使用10 mm厚的保温材料进行保护。
3.2实验结果及分析
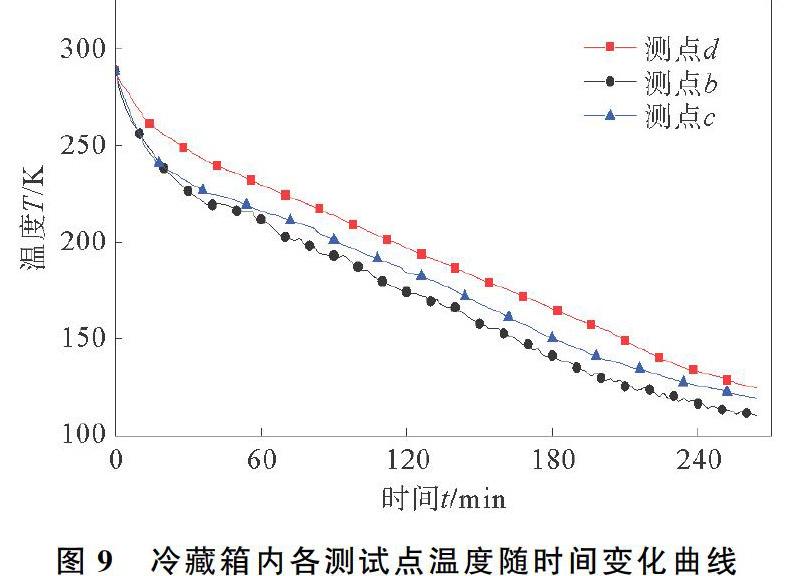
冷藏箱内各测试点温度随时间变化曲线如图9所示。由图9可以看出,冷藏箱制冷过程耗时264 min,箱体内平均温度由288 K下降至122.25 K,测点b、c、d的温度分别从288 K下降至110.62 K、119.8 K、124.7 K,温度由高到低依次是测点d(即冷藏箱内顶部),测点c(即冷藏箱内底部),测点b(即换热器管道出口处)。由于冷藏箱内传热方式主要为自然对流换热,降温过程中冷藏箱顶部与底部存在温度差,测点c、d测量温度平均温差为12.1 K。换热器出口温度始终低于冷藏箱顶部温度,在30 min之前,由于冷藏箱内温度与LN2温度温差巨大,换热器出口温度与冷藏箱底部温度相近,30 min之后,测点b和测点c的平均温差为8.8 K。在20 min之前,测点b、c、d温度变化较大,20 min之后测点b、c、d温度变化相对减小,变化曲线呈线性变化,这是由于PT100测点热惯性较大,冷藏箱内放置有回转式货架,货架温度在不断降低,而且换热器LN2入口流速并非定值。经测量,测点a,即LN2入口处平均温度为87.6 K,与LN2沸点存在10.6 K的温差,这是液氮罐与冷藏箱连接的不锈钢软管导致,管长约1 m;测点e,即缓冲间温度最低为258 K,最高为291 K,最低温度是由于冷藏箱漏冷与传动轴导热,最高温度是由于缓冲间内电磁阀与电机开启产生热量。
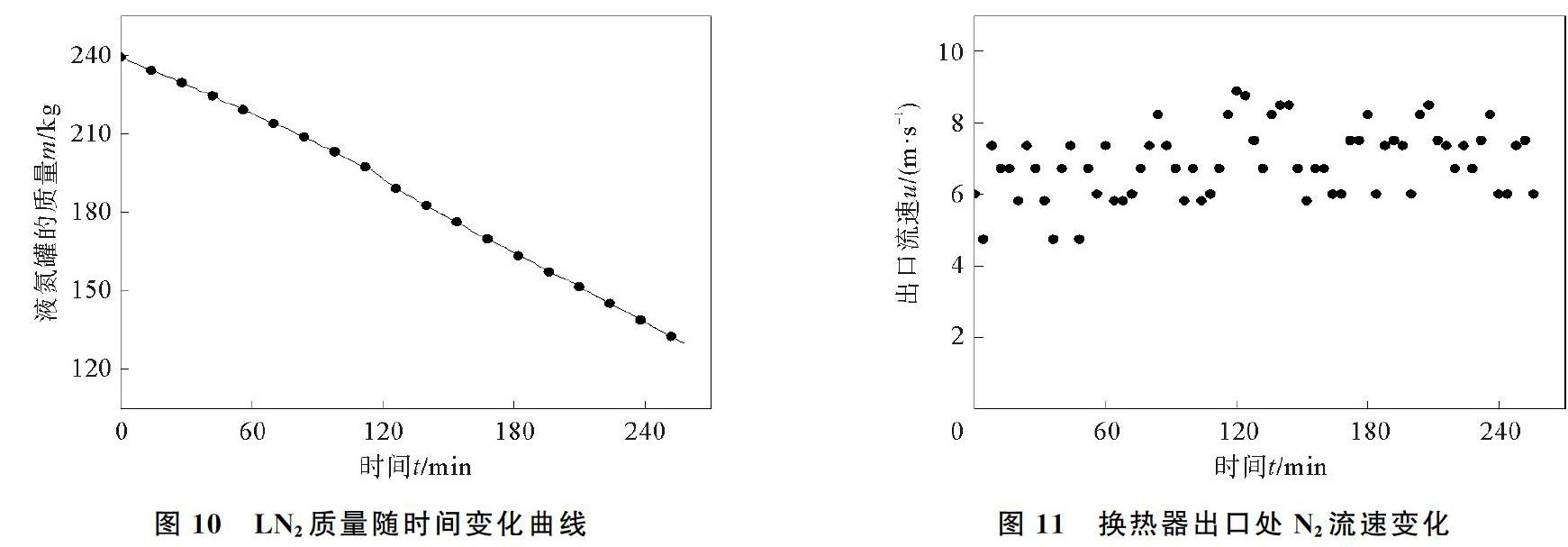
LN2质量随时间变化曲线如图10所示,换热器出口处N2流速变化如图11所示。
由图10和11可以看出,降温过程LN2共消耗110.94 kg,LN2平均入口流速为25.21 m/s;换热器出口处N2平均流速为6.5 m/s。经计算,实验过程冷藏箱平均制冷量为1 434.09 W,当LN2入口流速一定时,冷藏箱内温度越低,相对制冷量越小。
3.3数值模拟与实验对比
冷藏箱平均温度实验数据与模拟值对比如图12所示。由图12可以看出,两条降温曲线走势基本相同,在约30 min之前,冷藏箱平均温度模拟过程高于实验过程,这是由于实验过程箱体内温度测点位置所致,测点c的位置靠近进液管,测量温度相对较低;30 min之后,温度呈线性下降趋势,这是由于实验过程箱体漏冷与内部货架吸热所致。实验过程中,冷藏箱平均温度下降至123 K,用时264 min,模拟过程用时227 min,相差37 min,实验过程消耗LN2质量为110.94 kg,模拟过程消耗LN2质量为95.9 kg,相差15.04 kg。
整个降温过程中,实验值与模拟值存在一定误差,其原因如下:
1)实验过程由于自增压液氮罐内部压力不稳定与换热器分液管路安装位置的影响,换热器入口流量非恒定值,平均入口流量为12.5 kg/h,不同入口与不同时间入口流量波动较大,模拟过程换热器入口流量为定值。
2)实验过程由于液氮罐与冷藏箱连接软管有冷量损失,换热器入口处LN2温度比模拟过程温度较高。
3)实验过程冷藏箱内仅有两个PT100温度测点,测得温度分布不是非常精准,模拟过程在冷藏箱内设有15个温度监测点。
4)实验过程冷藏箱维护结构、门体及传动轴存在漏冷现象,箱内放置有回转式货架,模拟过程冷藏箱壁面假设为绝热。
5)实验过程换热器管道与翅片温度存在一定温差,模拟过程假设换热器壁面温度均匀。
4结束语
本文利用Fluent软件数值模拟与实验相结合的方法,研究了LN2深冷低温冷藏箱的制冷性能。模拟结果表明,低温换热器通过自然对流的方式与箱内空气进行热交换,换热过程中由于冷热干空气密度不同的原因形成涡流,从而导致箱体温度顶部高于底部、前部高于后部,低温箱内温度降至设计温度123 K,用时264 min,此过程消耗LN2质量为110.94 kg,模拟时间误差为16.3%,LN2质量误差为15.7%,拟合结果较好,为LN2深低温冷藏箱的设计提供了理论依据。本研究中低温换热器设计在低温箱的顶部偏后位置,箱内产生了一定的温度不均勻性,且降温时间较长,下一步重点研究低温换热器的安装位置以及结构设计,以达到加强换热以缩减降温时间。
参考文献:
[1]陈虹, 邹阳, 梁文清, 等. 液氮管道排空过程CFD模拟及分析[J]. 东南大学学报: 自然科学版, 2016, 46(6): 1246-1250.
[2]王世伟. 液氮制冷低温物流箱的设计与实验研究[D]. 天津: 天津商业大学, 2016.
[3]任泽霈, 张登富. 三维半封闭空间自然对流的流动与换热研究[J]. 工程热物理学报, 1990, 11(2): 188-193.
[4]徐瀚洲, 郭宪民, 王世伟. 液氮冷藏箱性能实验研究[J]. 低温与特气, 2020, 38(2): 29-32.
[5]王斯民, 厉彦忠, 文键, 等.竖直圆管内液氮过冷流动沸腾数值模拟研究[J]. 化学工程, 2008, 36(10): 17-20.
[6]陈叔平, 韩宏茵, 谢福寿, 等. 翅片管气化器管内相变传热流动数值模拟[J]. 低温与超导, 2012, 40(2): 52-56.
[7]Tavakoli R, Babaei R, Varahram N, et a1. Numerical simulation of liquid/gas phase flow during mold filling[J]. Computer methods in applied mechanics and energy, 2006, 196(1-3): 697-713.
[8]Herrmann M. A balanced force refined level set grid method for two-phase flows on unstructured flow solver grids[J]. Journal of Computational Physics, 2008, 227(4): 2674-2706.
[9]Jiang X, Siamas G A, Jagus K, et a1. Physical modeling and advanced simulations of gas-liquid two-phase jet flows in atomization and sprays[J]. Progress in Energy and Combustion Science, 2010, 36(2): 131-167.
[10]Klimenko V V, Fyodorov M V, Fomichyov Y A. Channel orientation and geometry influence on heat transfer with two-Base forced flow of nitrogen[J]. Cryogenics, 1989, 29(1): 31-36.
[11]任嘉友, 王子云, 齐润生, 等. 高封闭方腔自然对流换热特性数值模拟研究[J]. 热能动力工程, 2019, 34(12): 79-85.
[12]Chai X, Li W, Chen B, et al. Numerical simulation of turbulent natural convection in an enclosure with a curved surface heated from below[J]. Progress in Nuclear Energy, 2020, 126: 103392-103402.
[13]Souayeh B, Ben-Cheikh N, Ben-Beya B. Numerical simulation of three-dimensional natural convection in a cubic enclosure induced by an isothermally-heated circular cylinder at different inclinations[J]. International Journal of Thermal Sciences, 2016, 110: 325-339.
[14]熊莉芳, 林源, 李世武. k-ε湍流模型及其在FLUENT軟件中的应用[J]. 工业加热, 2007, 36(4): 13-15.
[15]张敏, 陶锴, 晏刚. 含内热源的梯形腔自然对流换热数值模拟[J]. 化工学报, 2011, 62(6): 1543-1548.
[16]周振君, 雷刚, 王天祥. 低温液氮贮箱增压性能及热分层研究[J]. 低温与超导, 2017, 45(1): 6-10, 37.
[17]杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 2006.
[18]陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2008.
[19]无锡市蓝星压力容器有限公司. 一种液氮深冷换热器: 中国, CN201420047731.7[P]. 2014-12-03.
[20]张周卫, 李跃, 汪雅红, 等. 低温液氮用系列缠绕管式换热器的研究与开发[J]. 石油机械, 2015, 43(6): 117-122.
Abstract: In order to solve the cryogenic storage problem of biological samples, a cryogenic chamber using liquid nitrogen refrigeration is designed in this paper, and the refrigeration performance of the cryogenic chamber is studied. Using the Fluent software to simulate software combined with practice, the method of simulation of cold box process of natural convection heat transfer in heat exchanger, it studied the LN2 cryogenic cooling performance of the cooler at low temperature, and predicts natural convection heat exchange time, the air flow pattern in the box and the consumption of liquid nitrogen. Combined with the simulation result, it studies the cooling performance of low temperature experiment research box, and compares the experimental data and simulation data. The maximum gas velocity was 0.24 m/s. The average temperature in the cryogenic chamber decreased from the initial temperature of 288.15 K to 123 K. It took 264 min and the average cooling capacity was 1434.09 kW. The process consumed 110.94 kg liquid nitrogen. This study provides a theoretical basis for the design of LN2 deep and low temperature refrigerator, which has certain application value.
Key words: liquid Nitrogen; cryogenic chamber; numerical simulation; refrigeration performance

