基于遗传算法的小型高增益阵列天线设计*

戴欣华 ，苏新彦 ，姚金杰 ，江润东 ，唐 强

(1.中北大学 信息探测与处理山西省重点实验室，山西 太原030051；2.西安机电信息技术研究所，陕西 西安710065)

0 引言

小型毫米波雷达在单兵雷达[1]、汽车防撞[2]、探测制导[3]等领域得到广泛应用。 而在此类应用中一个非常突出的问题是如何在狭小的安装空间内同时满足大探测范围和足够远的探测距离，对应天线的特性为高增益和宽波束宽度。因此设计满足高增益和宽波束宽度需求的阵列天线具有相当大的实际意义和工程价值。

文献[4]提出的一种四元并联馈电双天线阵，采用传统并联馈电设计阵列增益不足[4]；文献[1]、[2]中的串并联混合馈电设计都采用矩形栅格矩形边界阵，存在口径效率不足这个问题。 文献[5]采用加载寄生元件方法扩展了波束宽度，但当频率上升到Ka 波段时对加工精度的要求过于苛刻[5]。 提高增益的最直接做法是增加阵元数目，而增加阵元数目会降低波束宽度，因此在阵列天线设计过程中引入智能优化算法对阵列的性能进行优化十分必要。 以遗传算法为例，通常做法是将阵列的结构参数[6]、幅相分布[7]、相对位置[8-9]等作为优化变量，选取合适的选择、交叉、变异算子及策略获得满足设计需求的阵列天线。 在对文献[6]～文献[9]研究的基础上可知，工程实践中对遗传算法优化天线的具体方案不能以一概全，要根据具体情况采取最合适的设计方案。

本文开展了将遗传算法应用在天线优化中的研究并提出了一种运用于小型毫米波雷达前端的微带阵列天线，天线阵列采用串并联混合的馈电方式，通过遗传算法优化正交传输线的长度控制子阵列的相对位置，实现指定载体上小型化微带阵列天线高增益和宽波束宽度目标。

1 阵列天线设计

本文提出的天线所需要满足的具体指标包括收发天线阵列排布在直径为30 mm 的圆形基底内，天线中心频率为36 GHz，在中心频率36 GHz 增益大于12 dBi，E 面和H 面波束宽度不低于15°。 由此单个收发阵列约束在半径为15 mm 的半圆内，微带阵列设计为8 元，阵列分为两种子阵以及馈电网络共三部分。阵列天线的设计流程包括设计阵元和馈电网络，阵列分为串联子阵和并联子阵，互相之间通过子阵馈电网络进行功率分配。

1.1 阵元设计

根据工程经验选择厚度为10 mil、介电常数为2.2 的Rogers 5880 作为介质基板，铜厚1 oz，串联和并联子阵内的阵元略有不同，但是都可以用传输线模型进行分析设计。传输线法将矩形微带贴片看作场沿横边没有变化的传输线谐振器，沿纵向呈驻波变化，辐射主要由两开路端处的边缘场产生，因此，可以将矩形微带贴片表示为两条平行缝隙[10]。 贴片的尺寸由经验公式(1)～(4)估算：

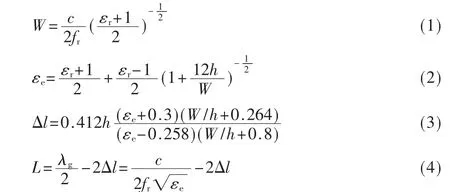
式中：W、L 分别为贴片辐射边和非辐射边的长度；fr是天线谐 振 频 率；εr、εe、h 分 别 为介质 的 相 对 介 电 常 数、等效相对介电常数和厚度；εr、Δl 分别是介质中的波导波长和开路端缝隙等效导纳的延伸长度。同时在馈电方式的选择上，串联子阵的阵元采用边缘馈电，并联子阵的阵元采用嵌入式馈电。 确定初始尺寸后，在仿真软件中微调使贴片在中心频率谐振。串馈两阵元及并馈阵元结构见图1。

1.2 串联、并联子阵设计

分别仿真串联子阵以及并联子阵。 串联子阵由两个矩形贴片组成，分别是传输单元和匹配单元，可以等效为4 元辐射电导谐振电路，根据1.1 节结果将初始尺寸带入子阵仿真，考虑到组阵后贴片之间互耦，沿微带线在每个贴片边设置探针检测谐振状态[11]，再微调阵元尺寸使得子阵在中心频率谐振。 并联子阵同理。 串联子阵为避免反射波同向叠加，串联馈电的两阵元间隔不是半波长的倍数， 因此波束不是指向边射方向而是倾斜的，且主波束随频率偏移[10]。 两并联子阵从输入端至各阵元等长，各单元同相，形成边射波束。

1.3 馈电网络设计

阵列采用50 Ω 同轴线经2.92 mm 连接器从底部馈电，馈电口距离板边0.5 mm，通过一段35.36 Ω 的四分之一波长阻抗变换器变换成25 Ω 后分为两路50 Ω，每一路再分别分为两路，一路为两贴片串联，另一路为两贴片并联。 并联子阵通过一段正交馈线与馈电点连接，通过优化正交馈线的长度控制串联子阵与并联子阵的相对位置从而优化阵列辐射特性。 由于阵列尺寸限制，串联子阵的安装空间较为狭隘难以做阻抗变换，在主馈线与串、并联子阵的连接处采取不等分功分器，由式(5)、式(6)通过改变传输线的特性阻抗调整功率分配比。根据串联子阵及主传输线宽度并考虑加工公差，并联子阵与串联子阵的功分比为1.3：1。 各馈线特性阻抗见表1。

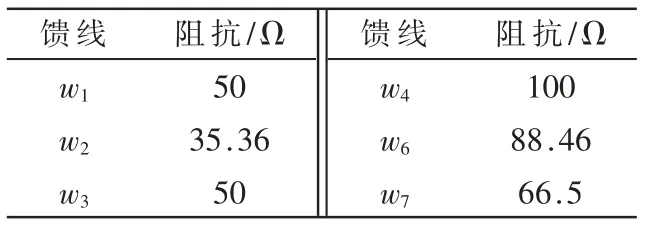
表1 各馈线特性阻抗

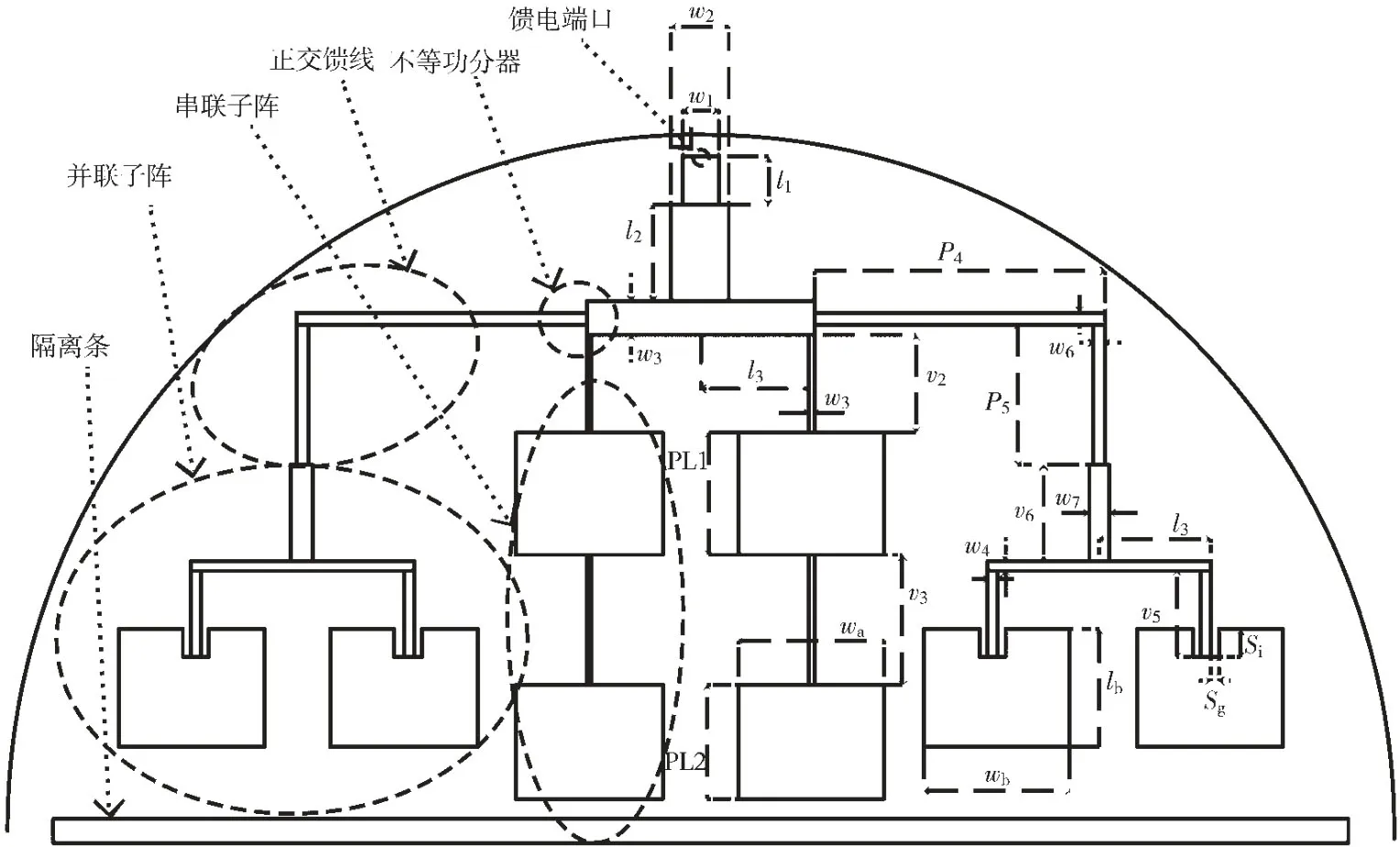
图1 阵列天线结构示意图

收发阵列之间放置0.5 mm 宽、28 mm 长的矩形条以提升隔离度，阵列设计完成之后的结构如图1 所示。

2 阵列天线优化

单个收发阵列若干随机阵元分布情况下的阵列谐振峰有多个且都不在中心频率，由此出现阻抗失配损耗，当阵元间距过大会导致出现栅瓣，这些都必然影响天线阵列的增益[12]。 因此有必要使用遗传算法进行优化布阵，以期在给定约束下确定天线阵列的物理布局，获取满足期望性能指标的辐射方向图。

2.1 确定优化变量

在子阵已经设计好的基础上，各阵元在各子阵中位置确定，只要确定子阵位置即可确定各阵元位置。 以子阵中两阵元的中点为圆心，用两阵元的外接圆作为子阵的模型，示意图如图2 所示。串馈阵只有一维自由度，并馈阵有二维自由度。根据子阵模型可以给出阵列的阵因子方向图函数：

式 中Pxn、Pyn为 阵 元n 的 位 置 坐 标，N 为 阵 元 个 数，θ、φ为阵面扫描角，In为阵元激励幅度，I0为阵元放置在原点的信号强度[13]。 由式(7)可知，阵因子方向图取决于阵元位置，串馈子阵的位置(x1，ya)由l3确定，并馈子阵列的位置(xb，yb)由P4、P5决定，将其作为决策变量。 约束条件包括子阵及馈电网络之间不能重叠且所有阵元及馈电网络都要在基底上以及根据工程实际要在板边留出安全距离。 据此计算后建立划分串并联子阵平面阵列形式下的优化模型见式(8)，模型中所用常量见表2。

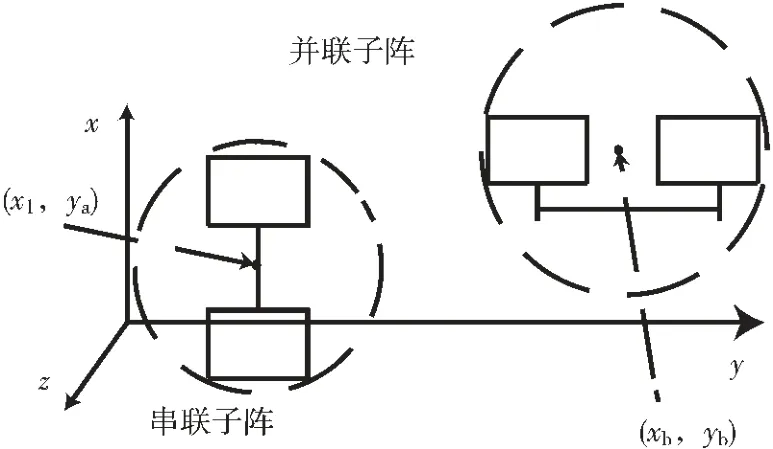
图2 子阵模型示意图

表2 优化模型常量表

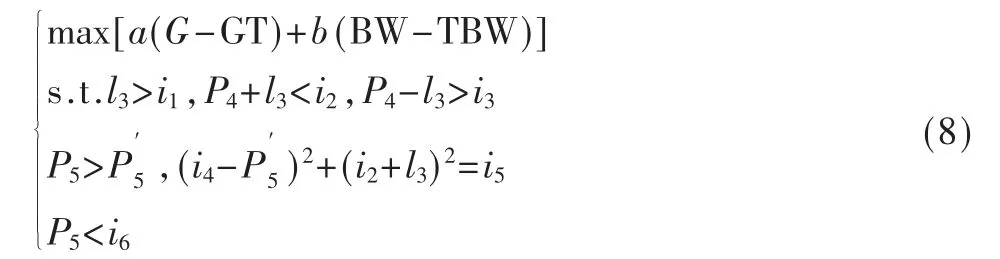
2.2 遗传算法优化

主馈电网络的优化变量是两串馈阵列的距离、两并馈阵相对于串馈阵的距离，子阵的各阵元之间存在互耦。由2.1 节可知，天线阵的各个参数并非独立地影响着天线的辐射特性，而是相互影响，相互作用，单独对相关参数进行分析很难得到较优的天线方向图性能。 在求解这种非线性多约束的多元组合优化问题上，智能优化算法具有独特的优势。 基于遗传算法对天线阵列进行优化。

采用的遗传算法流程如图3 所示，生成初始种群时群体规模NP 取100。 编码采用实数编码,将各优化变量作为基因构成染色体。 为了实现在对主瓣方向上的增益进行控制的同时实现需求的波束宽度要求，根据最大E面波束宽度、中心频率处最大主瓣增益构造适应度函数。

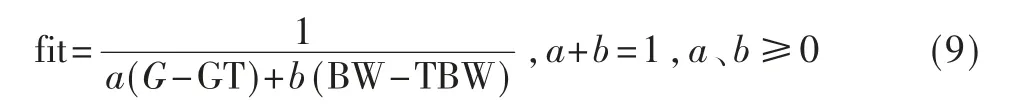
式中，G 为主瓣相对增益，GT 为目标主瓣相对增益；BW 为波束宽度，TBW 为目标波束宽度，G、GT、BW、TBW都采用归一化dB 值来表示。 通过调整加权系数a、b调整对增益和波束宽度要求的权衡，根据经验选取a=0.8，b=0.2。 波束宽度越大，增益越高，适应度函数越趋近于0。

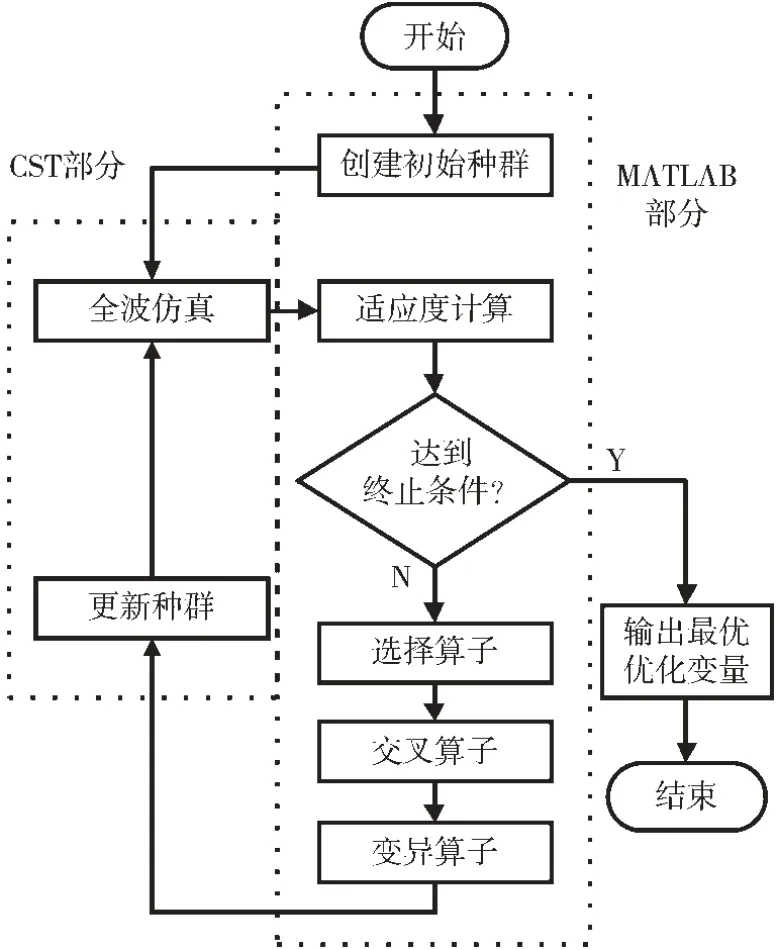
图3 遗传算法流程

随后对种群中的个体进行选择、交叉、变异的操作，选择和交叉操作采用“君主方案”，就是根据群体适应度值高低排序的基础上，用最优个体与其他偶数位的所有个体进行交叉，每次交叉产生两个新个体，交叉后对新产生的群体进行多点变异产生新群体，在计算其适应度值，然后和父群体合并，按照适应度值进行排序，选择前NP 个个体为新群体[14]。同时为了防止Pareto 最优解丢失并加速算法的快速收敛，参考非支配排序遗传算法(NSGA-Ⅱ)[15]，引入精英策略，保留父代中的优良个体直接进入子代，具体操作为在交叉、变异之后用父代最优个体替换新种群中的最差个体。交叉概率取0.5，变异概率取0.1。

遗传算法在MATLAB 中完成，将参数传递给CST MWS之后调用求解器进行全波仿真，随后提取CST 中中心频率处的方向图数据(波束宽度、增益)供MATLAB 读取，进行计算适应度值、选择、交叉变异的遗传操作。当获得全局最优解或达到迭代次数限制时停止迭代并输出优化变量。 优化完毕之后阵列天线的结构参数如表3 所示。

表3 天线阵列结构参数(mm)

3 仿真测试结果与分析

优化完毕之后更新结构参数进行全波仿真，在PCB加工后采用矢网测量反射系数曲线如图4 所示。 在微波暗室中测试天线实物如图5 所示，测试得到E 面、H 面方向图如图6、图7 所示。

图4 仿真及实测S11 曲线

阵列天线的-10 dB 阻抗带宽为6.94%(34.8～37.3 GHz)，反射系数与仿真结果相比有差异原因可能是所用2.92 mm连接头与天线的馈电点手工粘合导致损耗及测量误差。测试E、H 面波束宽度分别为28°、15°，与仿真值略有差异可能是加工精度不够导致。 在中心频率36 GHz 处测试得到最大增益为15 dBi，与仿真结果基本相符。

4 结论

图5 天线实物及暗室测试图

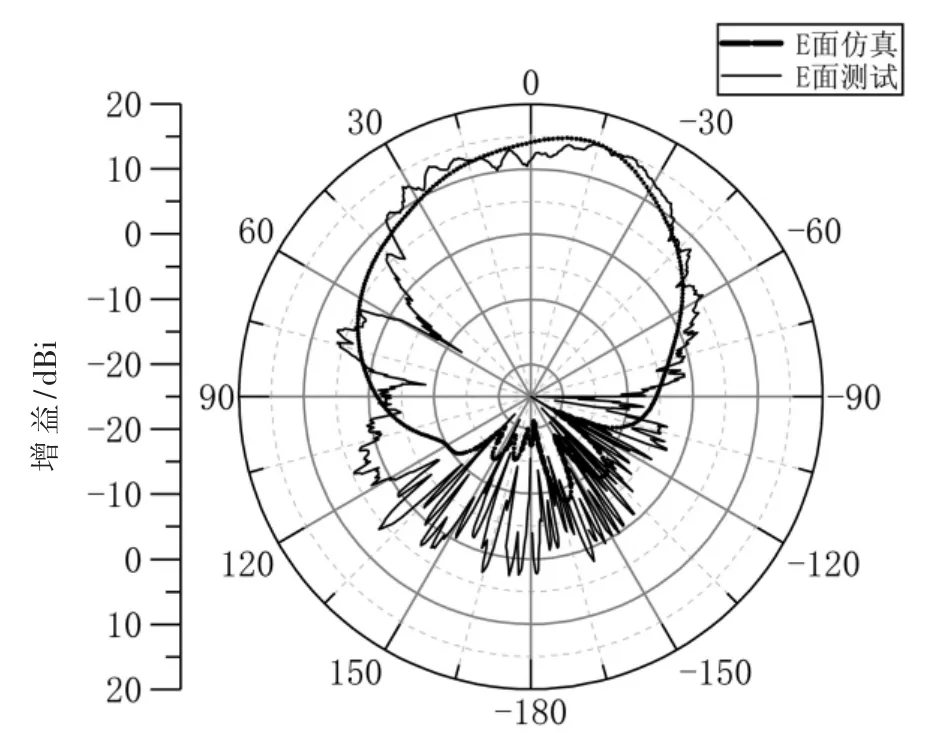
图6 E 面方向图

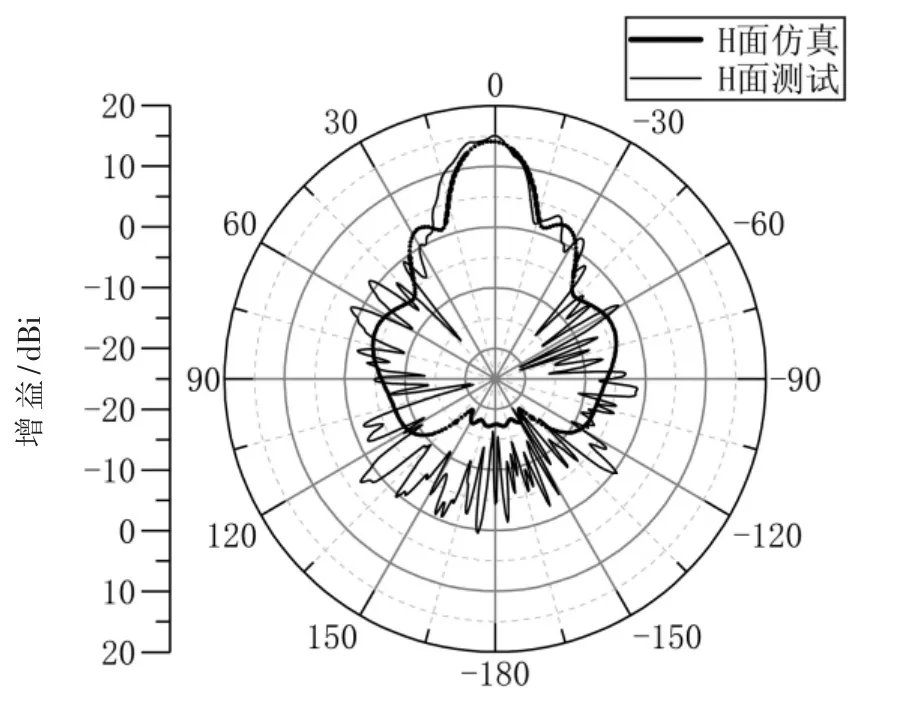
图7 H 面方向图

针对小型化毫米波雷达对大探测范围及远距离探测的需求，本文设计了一种Ka 波段小型高增益阵列天线，天线结构参数采用遗传算法优化，仿真及测试结果表明天线具有15 dBi 的高增益及在E 面28°、H 面15°较宽的波束宽度，可以应用在小型毫米波雷达及相关领域，具有一定的实际意义和工程价值。