铰接车橡胶弹簧悬挂系统非线性特性建模分析
谢 芳,翟振辉
(1.河南职业技术学院,河南 郑州 450046;2.河南工学院,河南 新乡 453003)
1 引言
悬挂系统对整车安全行驶具有重要作用,系统中弹性元件有钢质弹簧,其基本性能是线性的,非线性弹簧如空气弹簧、油气弹簧和橡胶弹簧,非线性弹簧用于车辆悬挂系统在国内外得到研究和开发[1]。橡胶弹簧悬挂系统结果简单且具有良好非线性刚度特性,减振性能良好,在非公路车辆、大型载重车辆和工程车辆中有广阔应用前景。因此,对橡胶弹簧悬挂系统非线性特征进行研究具有重要意义。
对悬架系统研究取得一定成果:文献[2]针对刚度的影响,建立了两自由度车辆模型进行分析;文献[3]通过对比分析,寻找提升悬挂系统建模精度的方法;文献[4]在室内整车道路模拟实验台上进行各种路面模拟试验,可预测车辆动力学性能指标;文献[5]采用Matlab 对不同方案的悬架系统进行对比分析。针对铰接式自卸车悬挂采用的橡胶弹簧悬架系统非线性特性进行分析,从橡胶弹簧的实际结构出发,通过静、动态试验,对橡胶弹簧的静刚度、动刚度及阻尼损耗因子等基本特性进行分析。在试验基础之上,同时基于有限元方法,建立橡胶弹簧的有限元模型,分析橡胶弹簧的结构参数与刚度的关系,为橡胶弹簧的工程设计提供依据。
2 橡胶弹簧悬挂系统试验分析
2.1 铰接式自卸车悬挂系统
铰接式自卸车悬挂系统,如图1(a)所示。前悬挂,如图1(b)所示。后悬挂,如图 1(c)所示。

图1 铰接式自卸车悬挂系统Fig.1 Articulated Dump Truck Suspension System
图1(a)弹性元件采用新型橡胶弹簧,悬挂系统有着明显优点。图1(b)由具有箱形断面形式“U”形架、横拉杆、四个沙漏式橡胶弹簧、四个液压减振器及二个橡胶缓冲器等组成。“确保车桥在一定范围的自由摆,以使两个车轮始终与地面接触。图1(c)“A”形架承受纵向力,横拉杆承受侧向力,橡胶复合弹簧则承受垂向力。
2.2 橡胶弹簧静态实验分析
橡胶弹簧是铰接式自卸车橡胶悬挂系统关键元件,对橡胶弹簧进行静动态试验并确定其静动态性能是整车悬挂系统动力学建模与分析的基础[6]。待实验的悬挂系统弹性元件,实验环境温度为19℃,如图2(a)所示。前悬沙漏式橡胶弹簧结构,如图2(b)所示。在对其按照上述过程进行试验时,将试验分为两组:一组为带上下钢套;另一组为不带上下钢套。带上下钢套的橡胶弹簧的静态实验过程,如图2(c)所示。从图中可以明显看出从轻载到重载的加载过程中橡胶弹簧的变形状况[7]。带有钢套和不带钢套的实验数据分别,如表1、表2 所示。

图2 橡胶弹簧及实验Fig.2 Rubber Spring and Test

表1 橡胶弹簧实验数据(带钢套)Tab.1 Static Experimental Results

表2 橡胶弹簧实验数据(不带钢套)Tab.2 Static Experimental Results
为得到载荷—变形曲线,对实验数据采用最小二乘法进行曲线拟合,这里采用3 次多项式拟合[8],得带钢套实验拟合方程:

式中:δ—变形。拟合残差平方和为1.5392。
对方程(1)求导,可求得橡胶弹簧的刚度:

不带钢套实验的拟合方程:

其残差平方和为3.6085。
拟和曲线,如图3(a)所示;可作出刚度曲线,如图3(b)所示。
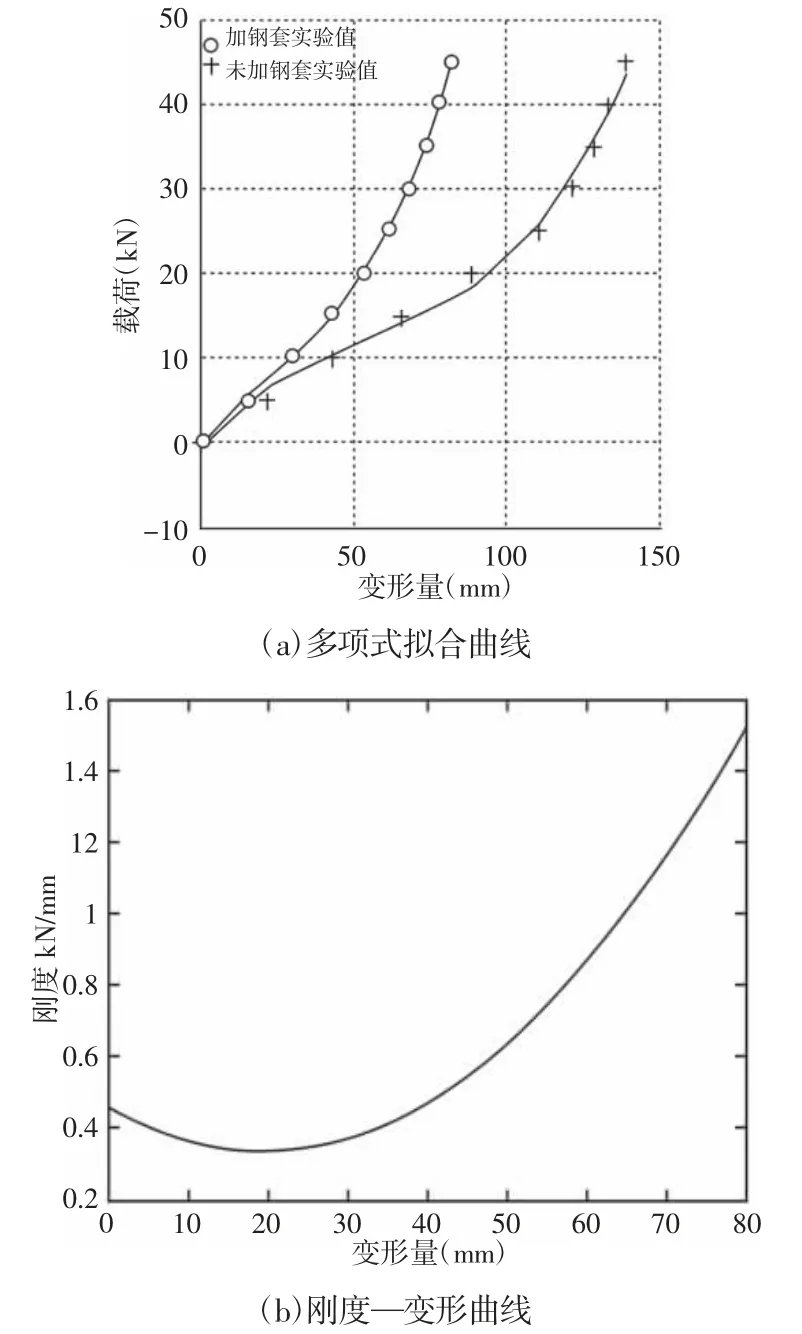
图3 橡胶弹簧多项式拟合曲线Fig.3 Rubber Spring Polynomial Fitting Curve
由图3(a)可知,钢套对橡胶弹簧刚度影响明显,特别是在外载大于10kN 区域,区别更大,当外载等于20kN 时,带刚套橡胶弹簧变形为52.765mm(三次平均),而未带刚套变形则达到88.078mm(两次平均)。带刚套刚度大于不带刚套的原因是钢套限制橡胶弹簧自由变形,减小橡胶弹簧可自由变形面积。橡胶弹簧实际工作状态是带刚套的。由图3(b)可知,在变形超过30mm,即载荷大于10kN,刚度随载荷增加而增大明显,有利于改善车辆平顺性。
2.3 橡胶弹簧动态实验分析
橡胶弹簧动态性能可用复刚度K*表示:

式中:K*—橡胶弹簧的同相动刚度;h—反映橡胶弹簧阻尼特性的正交动刚度,即结构阻尼系数;η—橡胶弹簧的阻尼损耗因子。
为了测定橡胶弹簧动刚度和阻尼损耗因子等动态性能,对橡胶弹簧进行动态实验[9]。设定实验参数,激励采用正弦波形式,振幅分别为0.2mm、0.5mm、1.0mm、1.5mm,频率范围从0.2Hz 开始,间隔0.2Hz,扫频到30Hz,静载设为5kN。由实验数据分别绘出在四种不同振幅下、选定频率范围内的动刚度、阻尼损耗因子及传递率曲线,如图4 所示。
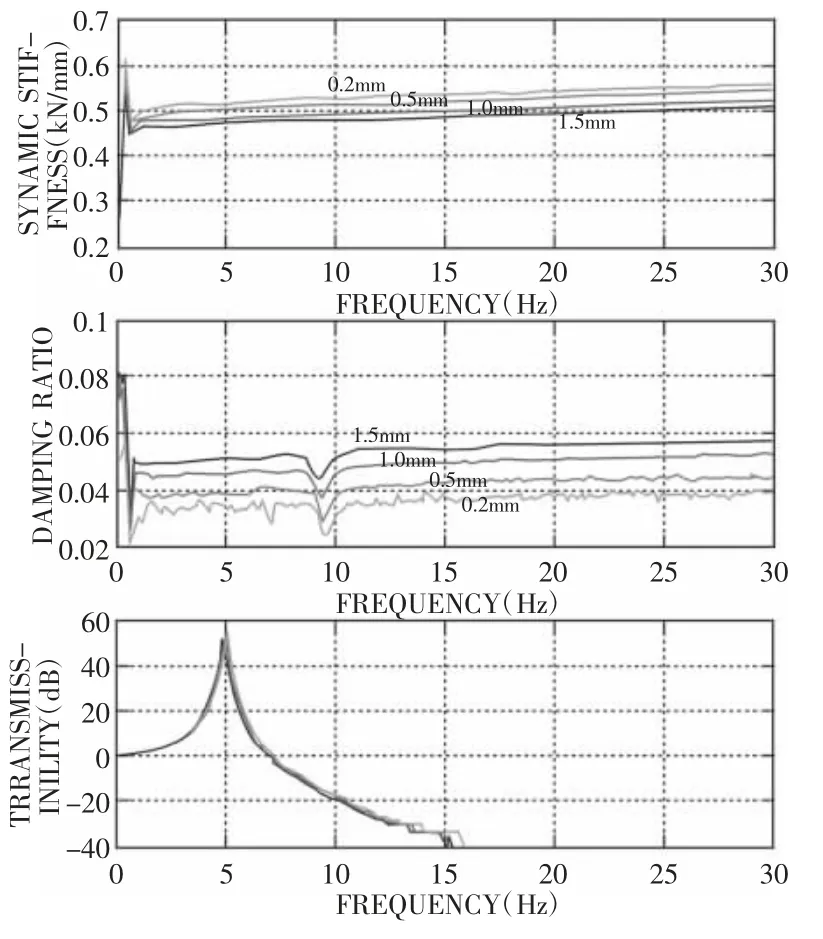
图4 橡胶弹簧动态特性曲线Fig.4 Rubber Spring Dynamic Characteristics Curve
由图可知,动刚度随着频率增加而略有增加,随着动载振幅增加而略有减小,从0.52kN/mm降至0.48kN/mm。阻尼损耗因子随频率增加而略有增加,随着动载振幅增加而增加,当动载分别为振幅0.2mm、0.5mm、1.0mm、1.5mm 正弦激励时,阻尼损耗因子约为0.036,0.04,0.05,0.055。动载振幅改变时,固有频率变化不大(因为动刚度变化不大),共振频率均出现在5Hz 附近。当动载分别为振幅0.2mm、0.5mm、1.0mm、1.5mm 的正弦激励时,共振传递率为552.65,670.84,276.75,356.28。从以上实验结果可以看出:橡胶弹簧的动态性能不但取决于频率,对振幅亦有较大的依从性。
3 橡胶弹簧有限元建模分析
3.1 前悬橡胶弹簧有限元分析
由于沙漏式橡胶弹簧结构和载荷(垂向工作载荷)都是轴对称的,因此对它进行轴对称分析[10]。同时,为了不同的计算精度、计算时间和后处理效果的不同考虑,分别建立平面和立体的模型进行分析。
在上钢套施加5kN、25kN、45kN,如图5 所示。平面分析结果,如图 5(a)、图 5(b)、图 5(c)所示。立体分析图,如图 5(d)、图 5(e)、图 5(f)所示。
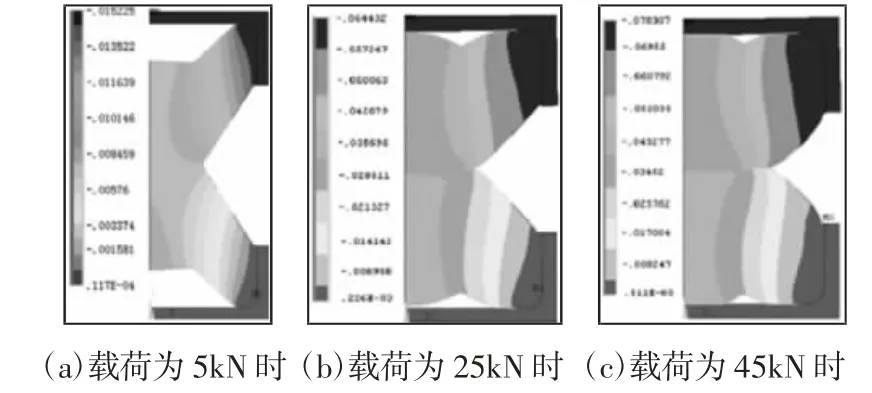
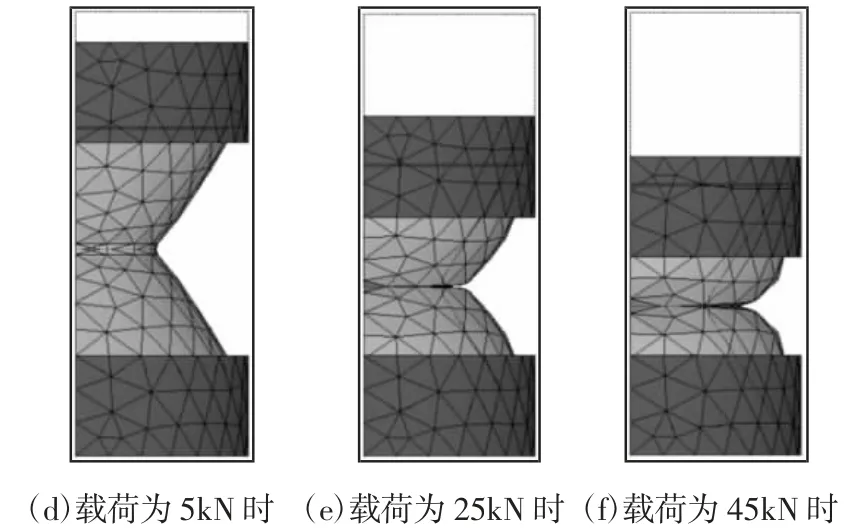
图5 橡胶弹簧变形图Fig.5 Rubber Spring Deformation
由图可知,随着载荷的增加,明显表现出非线性变化规律。有限元计算结果和橡胶弹簧试验结果的对比,如表3 所示。根据表3 中的数据可以做出橡胶弹簧载荷-变形曲线,如图6 所示。

表3 试验和有限元仿真数据对比(载荷kN,变形mm)Tab.3 Experimental and Finite Element Simulation Data Comparison

图6 橡胶弹簧载荷-变形曲线Fig.6 Rubber Spring Load-Deformation Curve
由图可知,橡胶弹簧变形表现较强非线性。试验与仿真结果基本一致。沙漏式橡胶弹簧不仅能提供三个方向挠度,轴向具有更大承载变形能力。在25kN 以后,几何非线性对总刚度的贡献很大。
3.2 后悬橡胶弹簧有限元分析
铰接式自卸车后悬架的弹性元件采用橡胶复合弹簧,结构如图7 所示。采用与前悬橡胶弹簧相同的有限元建模与方法,对后悬橡胶复合弹簧进行有限元分析,得到的载荷-变形数据,如表4 所示。对比图,如图8 所示。结果表明仿真预测结果是准确可靠的。

图7 橡胶复合弹簧Fig.7 Rubber Composite Spring

表4 橡胶复合弹簧载荷-变形数据(载荷kN,变形单mm)Tab.4 Rubber Composite Spring Load-Deformation Data
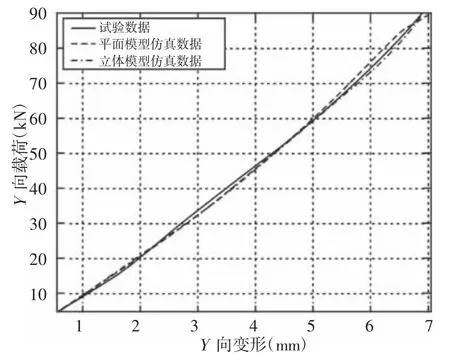
图8 橡胶复合弹簧载荷-变形曲线Fig.8 Rubber Composite Spring Load-Deformation Curve
4 结构参数对刚度特性影响
以橡胶弹簧有限元模型为基础,研究橡胶弹簧结构尺寸变化对刚度影响,从而为橡胶弹簧设计提供依据。以前悬橡胶弹簧为研究对象,如图9 所示。研究alpha 角、高度h2、连接半径RD3对刚度的影响。

图9 橡胶弹簧结构Fig.9 Rubber Spring Structure
alpha角与刚度关系以5°为一个梯度,改变橡胶弹簧alpha角,基于有限元模型,对橡胶弹簧力与位移关系进行仿真,绘制不同alpha 角情况下,力F与位移量L关系曲线,如图10(a)所示。通过改变h2值,采用有限元方法对橡胶弹簧力F与位移关系进了仿真,绘制不同h2情况下力F与位移量L关系曲线,如图10(b)所示。通过改变RD3 值,基于有限元方法,对力F与位移关系进行仿真,绘制不同RD3 对应力F与位移关系曲线,如图10(c)所示。

图10 结构参数对刚度特性影响Fig.10 Influence of Structural Parameters on Stiffness
从图10(a)可知,alpha 角影响非常明显;在力F不变情况下,随着alpha 角增加,压缩位移量减小,即刚度增大;随着alpha角减小,力与位移非线性关系越来越显著。因此,可以认为alpha角是设计前悬橡胶弹簧重要参数,且影响较大,既可决定橡胶弹簧刚度值大小,也决定非线性刚度曲线形状。从图10(b)可知,在力F不变时,随着h2增加,位移量呈上升趋势,即刚度有减小趋势,但同时也可看到,位移变化幅度不大,说明高度h2对刚度影响不如alpha 角大。随着h2增加橡胶弹簧刚度减小,主要由于h2是橡胶弹簧上下中心部位被挖去圆锥台高度,由于此部位有空间,当施加轴向力时,在外部有钢套约束情况下,橡胶弹簧就会向着内部空间膨胀鼓起,很显然,高度越大,可以提供橡胶膨胀的空间就越大,这样就容易被压缩,从而刚度就越小。从图10(c)可知,随着连接半径RD3 增加,在相同轴向力作用下,得到轴向压缩量呈减小趋势,而且可以看到随着RD3 增大,相同力作用下,带来位移量变小的值不是很大,因此转角半径的对刚度影响不显著。
5 结论
对铰接式自卸车前后悬挂进行分析,在试验基础上,基于有限元方法对橡胶弹簧非线性刚度特性进行建模与分析,并研究结构参数对其刚度特性影响。可知:(1)橡胶弹簧静态特性试验研究表明,橡胶弹簧刚度随着载荷增大而明显增大,这种非线性变化对整车平顺性有利。(2)橡胶弹簧动态特性试验研究表明,其动刚度和阻尼损耗因子与振动频率和振幅有很大关系。试验结果可作为设计选用橡胶弹簧的依据。(3)仿真获得刚度曲线与试验分析基本一致,表明橡胶弹簧理论分析和建模方法的准确可靠性。(4)不同橡胶弹簧结构参数变化对刚度影响也不相同,它们之间的关系可为橡胶弹簧刚度特性的设计提供依据。

