目标函数不确定性对流域径流预报效果的影响

夏 正 兵，邱 鹏

(江苏城市职业学院 建筑工程学院，江苏 南通 226006)

1 研究背景

作为模拟流域水文过程和揭示流域水资源丰枯状态的重要工具，水文模型被广泛应用于水文预报、水资源管理、气候变化和土地利用变化等方面[1-3]。然而，水文模型多基于大量数学方程对复杂流域水文过程进行抽象性描述，而大部分参数不能直接从流域特征中获取，必须采用人工或智能优化算法予以确定，以使模拟的水文过程尽可能接近流域实际的水文特性[4-5]。过去通常是采用单一目标函数评价模型的模拟精度，但众多水文模型参数率定结果表明：单一目标函数仅能反映流域水文特征的某一方面(洪量、洪峰等)，并不能够综合刻画水文过程中流域的全部水文特性[6-7]。比如，若选择相对误差(RE)作为目标函数，那么模拟结果在总水量上具有很好的性能，但在流量过程线形状和峰值流量上的性能会较差；若选择纳什效率系数(NSE)作为目标函数，则模型对高水流量较敏感，但会忽视枯水流量。

近年来，国内外学者针对多目标函数的水文模型参数率定过程进行了研究，并取得了较满意的结果[8-10]。例如，欧阳硕等[11]采用多目标文化自适应仿电磁学算法(MOCSEM)，对新安江模型进行了多目标参数的求解，结果表明，该方法可以同时权衡流域水文系统不同水文特性的参数组合方式。周建中等[7]采用多目标优化算法(MOSCDE)对新安江模型参数进行率定，结果表明，改进的非劣解选择方法能够有效地从大规模非劣解集中筛选出最优的非劣解。杜彦臻等[12]采用多目标混合复杂演化(MOSCEM-UA)方法来率定垂向混合产流模型参数，结果表明，采用多目标最优非劣解准则来选取最优解，使筛选结果更具准确性和可靠性。黄晓敏等[13]对比评估了NSGA-Ⅱ和MOPSO多目标的优化性能后发现，前者的非支配解的空间分布较后者相对均匀，即NSGA-Ⅱ的优化性能更优。徐帆等[14]以海河流域为研究对象，通过引入集成学习理论，将多目标NSGA-Ⅱ算法和集成学习相结合，有效地提高了洪水预测的泛化能力和预测精度。

以往的研究结果表明：采用多目标函数获得的模型模拟精度优于单目标函数，但在多目标函数的选择上存在着较大差异。同时，受近期气候变化和高强度人类活动的影响，流域或区域水资源在质和量上均发生了明显改变，目标函数选择的不确定性可能会影响到流域不同时期水资源的评估水平。因此，探究不同目标函数及其组合的不确定性对不同时期流域水资源评估的影响具有重要意义。

综上，本文以长江北岸的嘉陵江流域为例，利用流域内部及周边18个气象站点2006～2011年的日气象数据(降水、气温、风速等)和水文数据，通过设定不同目标函数及其组合方案集，采用多目标优化算法(NSGA-Ⅱ)来优化各方案下HyMod模型最优的参数组合，并将该优化结果与适应于单目标的遗传算法(GA)优化结果进行对比分析。在此基础上，量化评估了不同目标函数及其组合对不同量级流量和月尺度水资源评估的影响。

2 研究区域概况及数据来源

嘉陵江流域发源于秦岭北麓的代王山，干流流经三省一市(甘肃省、陕西省、四川省和重庆市)，流域支流较多，重要支流有八渡河、西汉水、白龙江、渠江和涪江等，干流全长1 345 km[15-16]。嘉陵江流域是长江上游的重要支流，也是三峡水库集水区域最大的一级支流，流域属于典型的亚热带气候区。年内水资源时程分布不均，年降水量主要集中在5～10月，略阳以上降水量较小，介于600～800 mm，中下游平原区约为1 000 mm。流域年潜在蒸发能力介于800～900 mm，多年平均径流量约为700亿m3。流域地理位置及其气象水文站点空间分布情况如图1所示。

图1 流域地理位置及气象水文站点位置空间分布示意Fig.1 Geographical location of the basin and spatial distribution of meteorological and hydrological stations

本文所采用的气象和水文数据包括流域内部及周边18个国家基准站2006～2011年逐日降水、风速、相对湿度、日照时数、气温等气象数据，以及同期流域出口控制站北碚水文站逐日实测流量数据，其中气象资料获取自国家气象共享服务网基准数据，水文数据获取自长江流域水文年鉴。

3 研究方法

3.1 概念式HyMod水文模型

HyMod模型是一种概念式水文模型，被广泛应用于水资源模拟、水文预报等方面，其产汇流过程主要包括高速流水箱产流和低速流水箱产流，采用蓄满产流机制[17-18]。HyMod模型满足的基本假定为：流域由无穷多个互不相干的点集合组成，且空间上任意一点的初始土壤蓄水量为已知，而且仅当净雨量P大于土壤有效持水能力(Cmax)时产流。同时，模型的蓄水能力曲线被假定为

(1)

式中：F为流域任意一点的累积蓄水能力；参数B为流域的蓄水能力变化系数；C为流域中任意一点的土壤蓄水能力。HyMod模型的产汇流过程结构如图2所示。

图2 HyMod模型的产汇流过程结构示意Fig.2 Schematic diagram of the production and convergence process of the HyMod model

3.2 多目标优化方法——NSGA-Ⅱ

NSGA-Ⅱ是针对NSGA 在非支配集构造、维持解集分布性策略中存在的不足所提出的改进算法[19]。该算法以聚集密度为目标，保证群体的多样性水平，其中聚集距离表示当前个体与相邻个体在每个子目标的距离和。非支配集的保存机制依据偏序关系，对于不同的子集选择排序小的子集，对于相同的子集保留聚集密度小的个体进入下一代。

3.3 多目标距离函数法

本文采用多目标距离函数法对Pareto集进行求解。该方法首先将不同目标函数值进行转化，目的是转化后的不同函数值到原点的距离相等[7]。具体为：以各个目标函数中最大的最小值减去其最小值，并修正目标函数到原点的距离。其计算公式为

Ai=max{Fj，min，j=1，2，…，n}-Fi，min

(2)

式中：Ai为目标函数i的转化常数；Fj，min为第j个目标函数的最小值；Fi，min为第i个目标函数的最小值；n为目标函数个数。

根据转化常数可以将不同目标函数进行聚合，其计算公式为

(3)

式中：Fagg代表参数组合θ下的聚合值。

通过式(2)将NSGA-Ⅱ得到的Pareto集合进行转化，就可以从参数空间中找到唯一一组最优的参数组合，即把多目标求解转化为单目标求解过程。

3.4 目标函数

不同目标函数反映了水文过程的不同特征，但多目标之间往往存在冲突。本文目标函数选取的同时考虑了：

(1) 模拟过程与实测过程水量的平衡。

(2) 模拟过程和实测过程的流量过程线形状一致。

(3) 洪峰流量、峰现时间吻合程度高，即均方根误差、高水流量误差系数和低水流量误差系数，3个目标函数的计算公式分别为

(4)

(5)

(6)

式中：Qobs，i为第i天的实测值，m3/s；Qsim，i为第i天的模拟值，m3/s；H为流量序列个数；N为场次洪水数；θ为模型参数组。

为了探究不同目标函数及其组合对不同量级流量和月径流量评估的影响，本文设定的目标函数组合方案集如表1所列。其中，F1、F2和F3方案采用广泛应用的遗传算法(GA)进行单目标模型参数优选，F1F2、F1F3、F2F3和F1F2F3组合方案则采用多目标NSGA-Ⅱ算法进行模型参数优选。

3.5 模型参数设定

(1) 目标函数F1、F2和F3为单目标，采用GA算法进行参数优选，其参数设定为：种群大小为200、最大迭代次数设置为10 000、交叉概率和变异概率分别为0.70和0.30。

(2) 不同目标之间的组合则采用NSGA-Ⅱ多目标算法，其参数设定为：种群大小设定为100次、最大迭代次数设定为10 000、交叉概率和变异概率分别为0.80和0.05，算法得到最大迭代次数时终止。

(3) 率定和验证的相关过程为：① 基于嘉陵江流域18个气象站点逐日降水、气温等资料，采用Penman-Monteith公式计算各站点的日潜在蒸发量；基于ArcGIS平台构建泰森多边形矩阵，计算流域面降水量和面潜在蒸发量。② 模型预热期为2006年，率定期、验证期分别为2007～2009年和2010～2011年。③ 将日面降水量和蒸发量数据分别输入到单目标和多目标模型中，分别采用单目标GA算法和多目标NSGA-Ⅱ算法进行率定期参数优选，将优选出的最优参数组合作为模型参数，并将其与验证期数据共同输入模型，进行模型性能验证。本文设定的目标函数组合方案集如表1所列。

3.6 模型性能评价指标

为了评估模拟值与实测值之间的差异，即模型性能评价精度，本文选取了纳什效率系数NSE、相对误差RE以及相关系数R2对模型性能进行适应性评价，其详细的计算公式参阅参考文献[2-3]。而且仅当NSE>0.5、RE<20%和R2>0.5同时得到满足时，才认为构建的嘉陵江流域HyMod模型是成功的。

4 结果与分析

4.1 不同目标函数组合下模型参数取值结果

表2为不同目标函数组合下模型参数的取值结果。由表2可以看出：同一参数在不同目标函数及其组合下，其取值差异不同，比如参数Cmax在F1、F1F3和F1F2F3目标函数下的取值基本一样，为18.63左右；但在其他目标函数组合下的取值差异较大，F2F3和F3下取值分别为5.31和28.71。这就意味着在不同目标函数下，模型参数参与水文过程的方式不同，参数值Cmax越大，流域产流方式更多是以蓄满产流为主，其参数值Cmax越小，则越易发生超渗产流。同时，参数bexp值越大，意味着流域内土壤含水量的空间变化性较大，即流量过程变化较快。总之，目标函数选择的不确定性直接决定着流域的产汇流方式，进而也会影响到流域径流模拟的精度。

表2 不同目标函数下HyMod模型参数取值结果Tab.2 Results of HyMod model parameter values under different objective functions

4.2 不同目标函数组合下HyMod模型性能评价结果

表3为不同目标函数下HyMod模型率定期和验证期模型性能评价结果。由表3可知：不同目标函数组合下，模型在率定期的径流模拟精度均优于验证期的径流模拟精度。单目标函数下，率定期和验证期考虑了实测水文过程和模拟过程吻合程度(F1)的目标函数获得的模型模拟精度最优，率定期和验证期NSE、RE和R2分别为0.70，0.10，0.85和0.69，0.12，0.83；而仅考虑洪峰流量拟合过程(F3)的目标函数得到的率定期和验证期NSE均在0.50左右，但模拟值与实测值的偏差却高达0.25。这就意味着单目标函数选择的不确定性将会给流域水资源的评估带来很大影响，应予以重视。

表3 不同目标函数下HyMod模型率定期和验证期模型性能评价结果Tab.3 Performance evaluation results of HyMod model rate under different objective functions

由多目标优化结果可以看出：不同目标函数组合下，若同时考虑实测水文过程与模拟水文过程的吻合程度(F1)，则率定期和验证期径流模拟的精度均较优，比如，率定期F1F2、F1F3目标函数下得到的NSE值均为0.71，验证期得到的NSE值则均为0.69。若未同时考虑F1目标函数，则模型模拟的精度较差，比如F2F3。若同时考虑F1、F2和F3，率定期和验证期得到的NSE值均会大于其他目标函数组合，且实测值与模拟值之间的偏差均小于其他目标函数组合。这就意味着采用多目标函数率定水文模型参数是十分重要的，也是必要的。

此外，多目标函数组合下(F1F2F3)得到的模型模拟精度均明显优于单目标模型的模拟精度，这一结果与周建中等[7]和杜彦臻等[12]研究得到的评价结果具有很好的一致性。

图3为不同目标函数下HyMod模型率定期和验证期的水文过程模拟结果。由图3可以看出：不同目标函数下，实测水文过程线与模拟水文过程线拟合程度较好，但在不同时段存在着明显差异。比如，单目标函数下：F2目标函数下得到的水文过程线在汛期对高流量的捕捉较差，洪峰流量明显被高估；而F3目标函数下得到的水文过程线对小洪水峰值流量的捕捉较好，但对高流量的捕捉同样较差。

图3 率定期和验证期HyMod模型在单目标和多目标下的水文模拟结果Fig.3 Results of calibration and verification period HyMod models under single and multiple objectives

由多目标函数下水文过程的拟合结果可以看出：F1F2F3目标函数下得到的水文模拟过程和实测水文过程基本一致，且对小洪水和大洪水的捕捉均较好；但在F2F3目标函数下得到模拟流量在非汛期(枯水期)明显被低估，这就意味着在不同目标函数下，水文模拟流量在不同时期对水文过程的捕捉能力存在较大差异，比如相较于单目标，无论是汛期还是非汛期，模拟流量过程线均与实测流量过程线的起伏变化一致；而单目标下的F3目标函数忽略了水量平衡因素，导致汛期(6～10月)洪量较小；F2目标函数忽略了洪峰流量拟合，导致汛期对洪峰的抓捕不准确。此外，对比多目标拟合结果可以看出：引入目标函数F1的情况下，汛期F1F2F3的性能劣于F2F3，表明引入过多的优化目标反而会降低优化结果的性能。因此，在采用多目标优化率定模型时，目标函数的合理选择也是十分重要的。

4.3 目标函数组合的不确定性对不同量级流量的影响

由前文可知：在不同目标函数下，水文模型侧重于捕捉水文过程的不同水文特征，这将会导致模型的模拟精度存在明显差异(由模型适应性评价结果可知)，但不易清晰看出目标函数组合的不确定性对不同量级流量的影响，因此，本节基于不同目标函数下的水文模拟结果，绘制出了其累积流量历时曲线，如图4所示。

图4 不同目标函数下水文模拟累积流量历时曲线Fig.4 Hydrological simulation cumulative flow duration curve under different objective functions

由图4可以看出：单目标时，10%～50%频率流量下，F1目标函数得到的模拟流量明显被低估，而F3目标函数下得到的模拟流量则存在着微弱的高估现象。同时，F3目标函数下显著低估了特大洪水量级，这从侧面验证了水文模拟过程对高流量的捕捉较差的结论。

由多目标的模拟结果可以看出：在F2F3目标函数下,水文模型得到的模拟流量在不同频率流量下表现形式差异较大，即高估高水流量、低估低水流量，这也是其水文模拟精度较差的主要原因。在其他目标函数下，水文模拟值与实测值误差较小。

4.4 目标函数组合的不确定性对月尺度径流预报的影响

基于不同目标函数下率定期和验证期的径流模拟结果，对比评估了目标函数组合的不确定性对月尺度水资源评估的影响，以期为流域水资源管理规划提供科学的参考。

图5为不同目标函数对月尺度模拟流量值的影响。由图5可以看出：

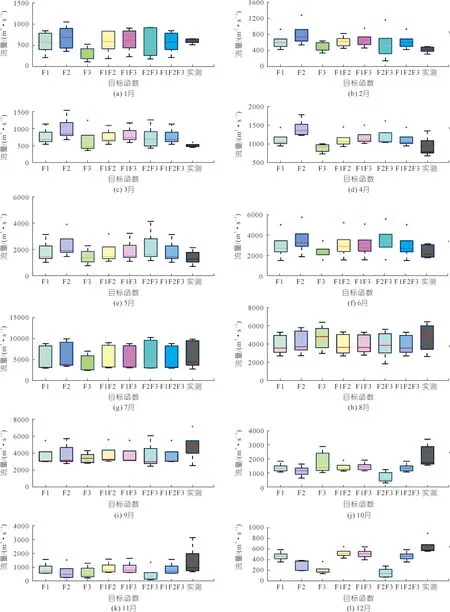
图5 不同目标函数对月尺度模拟流量值的影响Fig.5 Effects of different objective functions on simulated flow values on a monthly scale

(1) 不同目标函数下，月尺度模拟流量值与实测值之间差异的表现形式不同，但总体表现为，考虑多目标函数的模型模拟流量值与实测值之间的差异较小，而仅考虑单目标函数得到的流量值与实测值差异较大，尤其是在F3目标函数下，非汛期(10～12月份)明显低估了流域水资源量。

(2) 在非汛期(1～4月)，不同目标函数下得到的模拟流量误差范围明显要大于实测值的取值区间(由箱体宽度可知)，这可能归因于嘉陵江流域属于典型的亚热带气候区，受降水的时程分配不均影响(主要集中于5～10月份)而导致的；在非汛期径流量条件下，模型同时采用蓄满产流机制产流，对枯水流量的捕捉较差。

(3) 5～6月份，F2F3目标函数下得到的模拟流量明显被高估，尤其是6月份，其模拟值与实测值(中位数)差值高达2 350.00 m3/s；同时，8～12月份，模拟值显著被低估，尤其是10月份，其模拟值与实测值差值高达1 285.47 m3/s。

(4) 总的来说，采用不同的目标函数，可能在模型模拟性能评价结果上的差异较小，比如F1F2和F1F3，其率定期和验证期的NSE值相同，但不同时期在水资源评估方面却存在着较大差异。

综上所述，开展不同目标函数下不同量级和不同特征时期的流域径流预报分析，可有效提高流域管理机构的管理水平。

5 结 论

本文以典型的湿润区嘉陵江流域为研究对象，通过设定不同的目标函数方案集，分别采用遗传算法(GA)来优化单目标模型参数和采用NSGA-Ⅱ算法来优化多目标下的HyMod水文模型的参数。其次，对比分析了目标函数不确定性对模型模拟精度的性能评价结果，并探究了目标函数不确定性对不同量级的流量和月尺度水资源评估的影响。主要得到以下结论。

(1) 相较于单目标，同时考虑洪量和洪峰目标函数，可以有效提高水文预报精度；而仅考虑单目标时，则模拟值和实测值之间的误差较大。

(2) 不同目标函数在不同频率流量下的表现形式不同，当频率流量为10%～50%时，在F1目标函数下得到的模拟流量明显被低估，而在F3目标函数下则存在模拟流量被高估的现象。

(3) 采用不同的目标函数，可能在模型模拟性能评价结果上的差异较小，比如F1F2目标函数和F1F3目标函数率定期及验证期的NSE值相同，但在不同时期的径流预报方面，却存在着较大的差异。