列车管压强梯度对电空制动系统动力学影响

王振兴，郑永杰，康凯，任志国

（075000 河北省 张家口市 河北建筑工程学院）

0 引言

重载列车长度长、承重大，道路路况复杂、坡度大，只有通过精准操纵才能保证列车安全性。为了提升重载列车载重，我国采用了机车无线同步操纵技术（Locotrol）。该操纵系统虽可以改善制动性能，但Locotrol 制动系统依然将空气作为制动信号，并没有解决空气信号沿列车管传播速度有限的问题。20 世纪90 年代，美国开始研究在重载列车上使用ECP 制动系统[1]，该制动系统是通过电信号传递制动指令，近乎即时的传递速度是传统靠空气波传递制动命令的空气制动系统不能比拟的。目前已在美国、加拿大、南非、澳大利亚等国使用，并取得了很好的效果。但ECP制动系统结构复杂，需要改造现有车辆，成本较高，不易维护等缺陷限制了ECP 制动系统在我国推广的可行性。

如今提出一种与我国现有车辆完全兼容的电空制动系统，通过将车辆分成若干组，每组安装一套电控排气装置，通过压缩空气和电信号共同传递制动信号，即便在电控排气装置由于设备故障等原因而失效时，列车仍然能进行纯空气制动。电空制动系统既解决了兼容性问题又实现了靠电信号来传递制动信号，它对于我国开发新型制动系统有着重要意义。

随着计算机运算能力的提升，建立模型对重载列车动力学研究成为国内外学者的首选。Gruber[2]等提出将车辆作为刚体模型并只有一个纵向自由度，各刚体通过钩缓装置连接；Duncan[3]等利用仿真模拟方法对重载列车纵向冲动研究；Ansari[4]模拟了钩缓装置对列车车钩力的影响；C Cole[5]等通过仿真研究了轨道车辆在不同轨道上的动态轮轨接触应力。20 世纪90 年代起，国内学者开始纵向动力学研究。马大炜[6]通过对缓冲器冲击作用研究提出最大纵向力的化简算法；程海涛[7]等通过Newmark 显示积分法求得两车间最大纵向力；李显洲[8]通过MATLAB/Simulink 建立了完整纵向动力学模型；池茂儒[9]等利用循环变量法建立了重载列车三维空间耦合动力学模型。魏伟[10-11]、Wu Q[12]等应用流体动力学理论建立了重载列车制动管路及分配阀模型，并开发了Train Air Brake and Longitudinal Dynamics Simulation System（TABLDSS）仿真系统。

当列车通过长大坡道时，为了克服列车的自然加速度以保证限速，司机必须通过多次空气制动来调速。其特点是由减压制动、制动保压和缓解再充气组成一个制动周期的多次重复作用。为了尽快再制动，当列车再充气时间较短时，就会使得列车管中存在压强梯度，导致循环制动时制动缸压强不足，造成车钩断裂甚至脱轨。目前，国内外对列车管存在压强梯度时重载列车纵向冲动的研究还不够深入，只有文献[13]探讨了在列车进行纯空气制动时，列车管压力梯度对重载列车纵向冲动影响。本文利用在某仿真程序中已经建立的分组式电空制动系统模型计算了列车管压强梯度对采用电空制动系统的列车进行电空制动时纵向冲动影响。

1 电控排气装置物理模型

减小制动时的纵向冲动是长大列车安全运行急需解决的问题，仿真计算结果的准确性取决于电控空气制动模型建立得是否合适。列车中只有部分车辆安装了电控排气装置，对于没有安装电控排气装置的车辆使用原有的车辆制动系统模型，其工作原理在文献[14]中已详细介绍。图1所示为电控排气装置模型。

图1 电控排气装置控制模型Fig.1 Electronically controlled exhaust control model

图1 为带有电控排气装置的控制模型。将列车分为若干组后，在原有空气制动系统不改变的情况下，在每组中增加1 个电控排气装置、1 个中继机构和1 个均衡风缸，该排气装置通过接收机车发出的无线电信号控制排气装置的排气口。在常用和紧急制动时，机车信号发生装置发出无线控制指令，该无线控制指令包含减压量信号，排气装置接收到无线控制制动信号时，排气装置开始排出均衡风缸中的气，由于中继机构两侧存在压强差，列车管中的空气压力将中继机构中的活塞往上托起，从而促使下方排气口开放，使得列车管的风排入大气。当列车管中的空气压力减小到与均衡风缸一致时，中继机构会通过自身重力落下，关闭排气口，此时，列车管停止排风减压。当机车发出缓解信号时，电控制动装置接收到信号后，将列车管经过中继机构的充气孔与均衡风缸联通，实现均衡风缸充气功能，保证下一次制动时均衡风缸正常排风。

2 管路内压缩空气流动方程

计算管路内气体流动是建立空气制动系统模型的关键。制动系统内管路均为细长管，因此管内气体径向流动效应与纵向流动效应相比可忽略不计。假设管路的内壁是刚性的，管路内为一维、非等熵不定常的气体流动，而且在不计空气重力的情况下，根据气体流动的连续性、动量守恒定律和能量守恒定律建立方程组如下[15]：

上述方法不适用于边界点的情况，所以需要不同的边界条件建立相应的方程，空气制动系统中主要的边界条件如下：

（1）用于管路端部的封闭端边界方程为

（2）用于紧急制动和常用制动时列车管小孔排气方程为

（3）用于主管和支管连接处多分支边界方程为

（4）管路阻力边界方程（模拟软管连接器）为

（5）缸与管路连接边界方程为

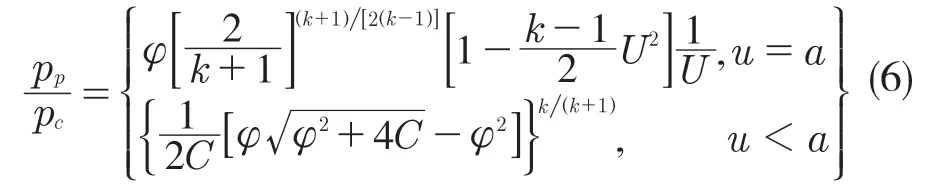
式中：U——无量纲速度；a——无量纲音速；φ——面积比；λ——黎曼变量；AA——熵；F——管接头面积；M——马赫数；pc——缸内气体压力；pp——管压力；pref——参考压力；φ——缸口面积比；k——阻力系数；C——无量纲速度相关的系数。变量中带*号——对应的变量除以熵值；下标N——接头处第N 个管端；下标in——入口处值；下标1，2——上流和下流。

各腔室内气体状态计算根据定容积开口系统热力学第一定律，即

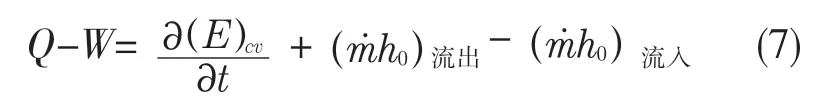
上述方程通过反复迭代利用数值计算方法求解。

3 分组式电空制动系统编组方案及仿真分析

图2 为列车分组式电空制动系统的编组情况。图2 中，J 表示机车，Z1，Z2…Zt 表示电控排气装置安装位置，N1，N2…Nn表示整个列车所含有的分组数。机车J 位于列车的第1 位置，第1 个电控排气装置安装在第2 位置，也就是第1节车辆上。按某工厂设计的每两节车为1 组，所以第2 个电控排气装置应安装在第3 节车辆上，第n 个电控排气装置则应位于第2n-1 节车辆上，如果列车中车辆总数为奇数，为防止列车出现紧急制动，则规定最后一组为3 节车辆。

图2 列车分组式电空制动系统的编组Fig.2 Grouping of train grouped electric air brake systems

电控排气装置靠电信号控制，理论上电信号传播时间差可忽略，但考虑到各个腔室滞后特性，假设电控排气装置初始动作时间有2 种：按某种波速均匀传递、按正态随机分布排气。均匀传递方式中，考虑传递波速：1 000 m/s；正态随机分布传递方式中，按随机变化范围为2 s 进行仿真。

当列车管定压600 kPa 时，列车缓解充气时间较短，为了能够尽快再制动，此时，首尾车辆列车管一定会存在压强差。为了研究列车管压强梯度对采用分组式电空制动系统列车的纵向冲动影响，本次仿真中计算了列车4 种不同梯度分布方式对带有电控排气装置的万吨重载列车纵向冲动影响。图3 绘制了4 种梯度方案：第1 种方案是列车管压强从首车600 kPa 降到尾车590 kPa且呈线性变化；方案2、方案3、方案4 分别为列车管压强从首车600 kPa 降到580，570，560 kPa，梯度均为线性变化。

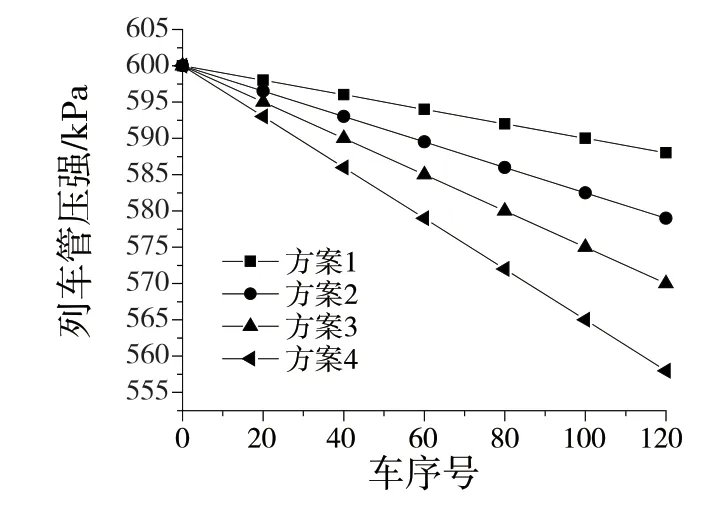
图3 4 种列车管压力梯度分布方案Fig.3 Four kinds of train pipe pressure gradient distribution scheme

4 计算结果及分析

本次计算列车为C80 万吨重载列车，列车编组为1HXD1+116C80，线路为平直线路。各车辆缓冲器类型、闸瓦类型及闸瓦摩擦系数均一致。由于列车在制动过程中主要表现的是压钩力，所以只对各个工况下压钩力进行比较，压钩力表现为负值。

图4 绘出了安装电控排气装置列车以匀速1 000 m/s 波速由前向后传播时列车管压强梯度对车钩力的影响。从图4 可见，当列车进行制动时，安装电控排气装置的列车以均速1 000 m/s 波速传播，电信号的传递方式是从前向后传播，前部车辆较后部车辆先制动，所以导致后部车辆向前涌，产生较大压钩力。

图4 顺序制动列车管梯度对车钩力影响Fig.4 Effect of pipe gradient of sequential brake train on coupler force

从图4 也可以看出，随着列车管压力梯度增大，列车各车位产生的最大车钩力也随之增大。当尾车列车管为理想压强600 kPa 开始制动时，最大压钩力为-288.9 kN。当尾车列车管压强分别为590，580，570，560 kPa 开始制动时，最大压钩力分别为-329.8，-375.9，-418.9，-449.6 kN，比理想工况尾车列车管压强为600 kPa 分别增加了14.1%，30.1%，44.9%，55.6%。随着列车管压强梯度的增加，分组式电空制动系统对列车纵向冲动减小效果逐渐减弱，但从图中还可以看出，4 种工况下进行常用全制动时最大车钩力发生车位一致，所以其制动过程制动机理一致。

图5 绘出了安装电控排气装置列车以随机2 s 制动时列车管压强梯度对车钩力的影响。从图5 可以看出，由于制动不均匀，相邻车辆的最大车钩力可能并不连续而是形成一些毛刺。因为电控排气装置随机动作，导致发生最大车钩力位置也是随机的，最大车钩力发生位置可能在中部也可能在尾部，这是由于在随机动作时，除了缓冲器特性以外，可能列车连续的某一部分车辆电控排气装置响应时间比较均匀，形成的制动力比较一致，对其前部车辆压扯造成压钩力的出现。在进行随机2 s 电控排气制动时，随着列车管压强梯度增大车钩力也随之增大。当尾车列车管压强为600 kPa 时，最大车钩为181.1 kN；当尾车列车管压强分别为590，580，570，560 kPa 开始制动时，最大压钩力分别为-183.6，-210.9，-291.9，-356.2 kN，比理想工况尾车列车管压强为600 kPa 分别增加了2.5，29.8，110.8，175.1 kN。

图5 随机制动列车管梯度对车钩力影响Fig.5 Influence of pipe gradient of train with random braking on coupler force

图6、图7 分别为当列车管存在压强梯度时，安装电控排气装置的列车采用顺序制动和随机制动时制动缸压强随车长变化曲线。横坐标代表车长，纵坐标代表制动缸平衡压强，曲线由尾车制动缸平衡压强区分。

从图6、图7 看出，当列车管存在压强梯度并进行常用全制动，沿车长方向制动缸稳定时压强数值越来越小，但对首车并没有影响，不管尾车开始制动时列车管压强为多少，首车制动缸稳定时的压强均为474 kPa。当尾车列车管压强为理想工况600 kPa 时，采用分组式电空制动系统制动（顺序制动和随机制动），首尾车制动缸平衡时压强几乎一致；当尾车列车管压强分别为590，580，570，560 kPa 进行电空制动时，尾车列车管压强每降低10 kPa 则制动缸平衡压强大约降低8 kPa。采用分组式电空制动系统虽然可以使首尾车制动缸动作时间差减小，有利于提高制动同步性，但并不能改变制动缸平衡时的压强大小。随着列车管梯度压强越来越大，列车后部车辆制动缸稳定压强越来越小，从而使得制动力沿车长越来越小，由于压强梯度的存在使得列车前部制动力大于后部制动力，制动时前部车辆制动能力比后部车辆强，最终导致列车纵向力增大。

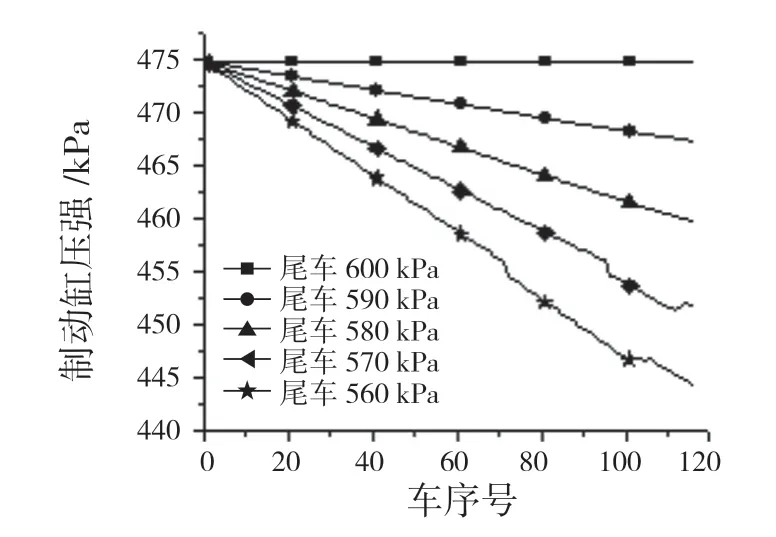
图6 顺序制动列车管梯度对制动缸压强影响Fig.6 Influence of pipe gradient of sequential brake train on brake cylinder pressure

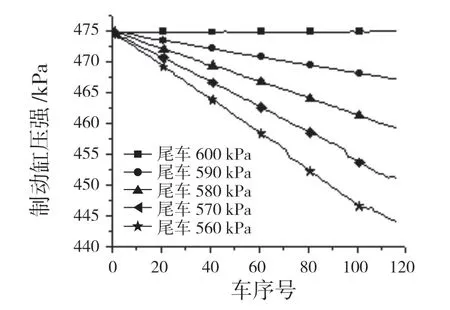
图7 随机制动列车管梯度对制动缸压强影响Fig.7 Influence of pipe gradient of random brake train on brake cylinder pressure

5 结论

（1）首尾车列车管压强梯度相差越大，电空制动时最大车钩力值越大；

（2）首尾车列车管压强梯度每增大1 0 kPa，电空制动时尾车制动缸平衡压强差则减小8 kPa；

（3）列车管压强梯度对首车制动缸平衡压强没有影响。