车身焊点布置优化研究

冯赛，徐家川，李迪，杨磊

（255000 山东省 淄博市 山东理工大学 交通与车辆工程学院）

0 引言

随着汽车行业竞争越来越激烈，降低生产成本和提高生产效率一直是汽车研发中心攻克的重要方面。焊接作为生产的重要一环，其焊点优化布置成为重点改进目标。白车身焊点数量巨大，如何准确有效地对焊点进行优化布置，对保证甚至提升原有结构性能并尽可能减少生产成本具有重要意义。

一段时间以来，国内外各大主机厂研发部门对优化焊点布置投入了大量人力物力，主要以拓扑优化的方法为指导进行优化，并获得了不错效果。D.M.Junqueira[1]等运用数值模拟和拓扑优化的方法找到最佳焊点分布，并保证扭转刚度保持在规定范围内；Ann-Britt Ryberg[2]等提出了3 种优化车身结构焊点数量的方法，证明了拓扑优化方法的效率更高；Leonardo Coriteac[3]等证明了利用CAE 优化算法可以在大幅度减少点焊数量的同时不损失性能和功能；屈新田[4]等通过HyperWorks/OptiStruct对车门焊点进行拓扑优化，并依据优化结果结合工程经验调整焊点布置；钱银超[5]等利用OptiStruct 对前减震器塔座焊点布置进行了拓扑优化分析，通过找到冗余焊点，结合焊点疲劳的计算结果确定出最终的优化方案；胡朝辉[6]等提出了一种基于焊点间距参数化的焊点布置优化方法对焊点布置方案进行优化；刘亮亮[7]利用软件OptiStruct 对不锈钢车体中的部分焊点进行了拓扑优化，在满足相关安全标准的前提下，该部分焊点得到大幅度减少，且优化后车体结构的强度刚度没有明显减弱。

在设计白车身的中后期，研发部门凭借对车身结构性能和工艺经验对焊点进行初步布置。此时的车身性能如刚度、模态等大致在设计要求之间，但基于经验的焊点布置不能保证车身性能和焊点数量最优，且优化后较少对比验证拓扑优化与其他方法优化的优越性，这就需要对焊点布置进一步研究。

本文依据拓扑优化仿真结果进一步优化焊点，删除筛选出的低密度单元焊点55 个，通过仿真对比分析其性能，证明在保证原有性能基础上减少焊点的可行性，达到了节约成本和提高生产效率的目的。车身焊点布置优化设计方法如图1 所示，主要包含以下步骤：建模、静刚度以及模态分析、焊点拓扑优化、基于不同方案对焊点优化对比分析。

图1 焊点拓扑优化研究流程图Fig.1 Flowchart of research on topology optimization of solder joints

1 焊接原理及模拟焊点选择

1.1 焊接原理

焊接是通过加压或加热、或两者并用，加或不加填充材料，使分离的金属表面达到原子间的结合，形成永久性连接的一种工艺方法[8]。焊接方法依据加热金属的热源性质、是否采用加压以及形成接头的状态划分。常用的焊接方法有很多，如熔化焊、压力焊以及钎焊等等，点焊属于压力焊的一种。焊接方法分类如表1 所示。

点焊是工件组合以后通过电极施加压力，利用电流流过接头处的接触面及邻近区域产生的电阻热进行焊接的方法[9]。点焊主要历经4 个阶段，分别是预压程序、焊接程序、维持程序和休止程序。在预压阶段只对母材金属施压，不通过电流。在焊接程序以及维持程序阶段，压力达到一定程度时，通过电流产生的热量融化母材金属，从而形成熔核。到达休止阶段时停止通电，压力也在逐渐减小[10]。

表1 焊接方法分类Tab.1 Classification of welding methods

点焊在车身焊接中运用广泛，如应用于焊接车身总成、车身侧围等分总成以及小型板类零件等。

1.2 有限元软件中的模拟焊点选择

不管是对焊点自身的疲劳、断裂等失效仿真所运用的焊点精细化模型，还是车身有限元分析中用到的焊点简化模型，都对仿真精度有不同程度的要求。因此，为得到更准确的仿真分析结果，需要针对不同的情况选取有效模拟真实焊点的焊点有限元模型。在有限元仿真软件中，常用的点焊结构仿真模型主要有RBE2，ACM，RBAR 和CWELD 等[11]。

综合考虑精度和效率，焊点较多的车身适合优先采用可变形梁单元、ACM2 单元以及CWELD 单元，其优缺点如表2 所示。CWELD 优点众多，如建模简单、对网格要求宽泛且能精准模拟焊点位置。为保证精度且减少计算时间，本文采用CWELD 模拟焊点。

表2 不同焊点的优缺点汇总Tab.2 Summary of advantages and disadvantages of different solder joints

2 车身多工况有限元分析

2.1 车身有限元模型建立

本文的有限元分析模型为某车身简化模型，大部分采用壳单元shell 建模，内外板主要采用钢材料，材料卡片为 MAT1，即材料属性不随温度变化的各向同性材料，泊松比为0.3，密度为7.85e-03 kg/m3，弹性模量为2.1e+05 MPa。整个模型节点数为335 371 个，单元数为326 214 个，CWELD 单元数为3 481 个，焊点分布如图2 所示。

图2 焊点分布Fig.2 Distribution of solder joints

2.2 车身多工况建立

本文主要对扭转工况、弯曲工况以及模态工况进行建立。

（1）弯曲工况。本工况主要模拟汽车在水平直线的路面行驶条件下车身结构受载时的情况。弯曲工况约束以及载荷建立：用RBE2 抓取各减震器的安装点，约束前减震器安装点连接中线Z 方向的平动自由度；约束后减震器安装点全部自由度。在左右门槛梁对应于B 柱中心的位置，用RBE2 抓取3×3 或2×4 个单元格，再通过RBE2抓取这两个RBE2的主节点，形成刚性连接，在最后生成的主节点上施加Z 向载荷-3 000 N。

（2）扭转工况。本工况主要模拟车辆在行驶过程中遇到轮胎悬空或抬高时的情况。扭转工况约束以及载荷建立：约束前减震器安装点连接中线Z 方向的平动自由度；约束后减震器安装点全部自由度。在前减震器安装点处施加Z 方向载荷，两载荷大小相等均为2 832.5 N，方向相反。

（3）模态工况。模态分析主要研究车身结构振动的固有频率和相应振型，为避免车身共振和降低噪声提供支撑。新建EIGRL 卡片，提取10～80 Hz 范围内的无约束自然模态频率。车身结构有限元模型及其部分载荷和约束如图3 所示。

图3 车身结构有限元模型及其部分载荷和约束Fig.3 Finite element model of body structure with partial loads and constraints

2.3 车身有限元仿真结果

通过HyperMesh/Optistruct 计算得到车身结构在弯曲、扭转工况下的变形云图和应力云图，以及一阶模态振型云图，有限元分析结果如图4所示。

图4 不同工况下的变形云图、应力云图以及1 阶模态振型云图Fig.4 Deformation cloud diagram,stress cloud diagram and first-order mode shape cloud diagram under different working conditions

从图4 可以看出，对于弯曲工况，车身B 柱、门槛梁以及门槛梁与地板交接等处变形较为明显，车身最大变形量为0.535 mm；车身应力则集中在门槛梁处，车身最大应力为154.8 MPa。对于扭转工况，车身的较大变形主要集中在A 柱、前纵梁等处，车身最大变形量为4.290 mm；车身应力集中在A 柱与前围上板交接等处，车身最大应力为281.4 MPa。对于模态分析，一阶模态频率为33.697 Hz，振型为前围上板沿Y 轴弯曲。

3 车身焊点拓扑优化

3.1 车身焊点拓扑优化模型

拓扑优化以车身焊点体积最小为优化目标，以保证弯曲刚度、扭转刚度以及模态频率为约束条件，设计变量为焊点单元密度，建立车身焊点拓扑优化数学模型为

2) 2017年8月21日15时，系统中W136号仪表连续出现传感器/变送器通信失败，变送器初始化，驱动超出量程，驱动增益低等4个关键报警信息。经排查为核心处理器故障，成功避免交接双方出现计量纠纷。

式中:xj——设计变量；m——设计变量个数；f（xi）——焊点体积目标函数；gi（x）——约束函数；——约束的上下极限；n——约束函数个数。根据2.3 节得到的车身静刚度与模态分析结果，为尽量保持原有性能，设置约束条件为：一阶模态大于30 Hz，扭转工况变形量小于4.4 mm、应力值小于285 MPa，弯曲工况变形量小于0.6 mm、应力值小于160 MPa。

3.2 车身焊点拓扑优化参数及优化结果

变密度法经常运用到Optistruct 拓扑优化当中，其基本思想是将有限元模型设计区域内的每个单元密度作为设计变量，密度值在0～1 范围内连续变化。当拓扑优化后的单元相对密度近似于0 时，表示去除该单元；当单元相对密度接近于1 时，表示保留该单元。通过引入惩罚因子，达到减少中间密度的目的，得到更接近于0 或1 的离散变量。

在变密度法拓扑优化中，惩罚因子的阈值至关重要。当惩罚因子过大时，优化时间长且不易收敛；当惩罚因子过小时，拓扑优化结果存在过量中间密度单元。通过不断仿真分析，本文涉及的车身模型更适宜将惩罚因子设为 6，使得计算过程时间短收敛快，且得到的计算结果里包含的中间密度单元较少。

本文在已经优化的基础上再优化，且只考虑部分CWELD 焊点，所以优化后的焊点主要分布在相对密度为0.7～1.0 的区间，这就保证了单元相对密度接近1.0，有利于焊点的拓扑优化[12]，为第4 节优选焊点提供有力数据，拓扑优化后焊点相对密度分布见表3。

表3 拓扑优化后焊点相对密度分布Tab.3 Relative density distribution of solder joints after topology optimization

4 基于拓扑优化焊点优选对比研究

经过上一节车身焊点拓扑优化，得到相对较优的焊点密度分布，虽然密度在0.7～1.0 区间内的焊点占比约96%，但仍需分析中间密度单元存留问题。本节采用删除单元密度较低焊点和随机删除冗余焊点两种方案，以此验证基于拓扑优化焊点的优越性，分别以优化方案1、方案2 区分。

对于优化方案1，首先在HyperViews 查看拓扑优化结果，用Query 筛选出密度较小的焊点ID，再通过HyperMesh 的删除Delete 功能中elems →by id 输入筛选好的焊点ID，以此缩减影响车身结构性能较小的某些局部部位的焊点。待优化焊点分布如图 5 所示，其中图5（a）对应图5（c），均为x-y 平面上的焊点分布；图5（b）对应图5（d），均为x-z 平面上的焊点分布。从两组对应焊点分布图可以看出，删除的焊点主要分布在车身前部性能影响较小的区域；对于优化方案2，则直接运用HyperMesh 的删除Delete 功能去掉排布较密焊点，如减少A，B 柱与地板焊接接头处、门槛梁和前纵梁处的焊点数量。通过调整焊点密度，两种优化方法焊点均减少55 个。

为验证基于拓扑优化的焊点调整优越性，分别对两种方法优化焊点后的车身进行多工况多性能仿真，仿真结果对比如表4 所示。

由表4 模态分析结果可知，2 种方案的1 阶模态频率都有不同程度降低，分别为0.03 Hz和3.778 Hz。该款汽车激振频率为23～25 Hz，虽然方案2 的1 阶模态频率仍高于激振频率2 Hz以上而不产生共振，但远不如方案1 稳定。

表4 两种方法优化焊点后的车身多工况仿真结果对比Tab.4 Comparison of simulation results of the two methods for optimizing solder joint under multiple working conditions

图5 原始焊点与待优化焊点分布对比Fig.5 Distribution of original solder joints compared with that of solder joints to be optimized

从扭转工况结果分析可知，方案1 的最大变形量相比优化前减小0.001 mm，几乎保持不变，方案2 最大变形量则增加0.066 mm；最大应力值前者保持不变，后者则相较增加0.5 MPa，误差较大，由此可知方案1 更具优越性。本文以2 种方案优化下扭转工况的变形云图与应力云图为例对比，如图6 所示。

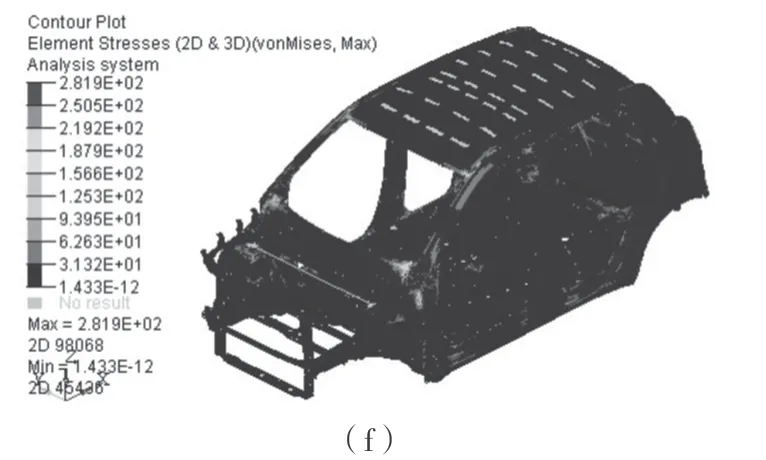
图6 不同优化方法下的扭转工况变形云图与应力云图对比Fig.6 Comparison of deformation cloud map and stress cloud map under different optimization methods

从弯曲工况结果来看，方案1 的最大变形量相比优化前减小0.002 mm，相对误差仅为-0.04%，方案2 最大变形量则增加0.017 6 mm，相对误差为3.29%；最大应力值前者几乎保持不变，后者则相较增加0.5 MPa，误差较大。由此方案1 更具有优越性。

由仿真结果对比分析可知，经过方案1 优化后的车身性能与原车身性能相比误差较小，相对误差均在0.1%以内，方案2 各指标相对误差均较大，由此验证了基于拓扑优化车身焊点的可行性，符合汽车轻量化设计的要求。

5 结束语

本文以某简化车身为研究对象，建立车身焊点拓扑优化数学模型，拓扑优化的优化目标为车身焊点体积最小，以保证甚至提高弯曲刚度、扭转刚度以及模态频率为约束条件，焊点单元密度为设计变量，得到焊点拓扑优化仿真结果。通过优化影响车身性能较小区域焊点使其焊点间距增大，并对车身性能进行对比分析，得出以下结论：

（1）通过拓扑优化后得到不同的焊点单元密度分布为研究对象，主要以合理减少中间单元密度的焊点为出发点进行优化，如增大影响车身性能较小区域的焊点距离。通过对比删除单元密度较低的焊点和随机删除冗余焊点2 种方案，可知在满足节约成本的同时，基于拓扑优化后的焊点分布比随机删除冗余焊点布置更能满足车身性能要求。

（2）通过变密度法拓扑优化，车身结构整体性能如刚度、模态等满足要求，1 阶模态频率、扭转工况以及弯曲工况下的最大变形量和最大应力值的相对误差均在0.1%以内，证明了其可行性。不仅车身性能得以保证，而且减少了车身焊点的数量，达到了车身轻量化以及节约焊接成本的效果。