高压转子组合不平衡量对发动机振动的影响分析
□ 王洪明
中国航发沈阳黎明航空发动机有限责任公司 沈阳 110043
1 分析背景
高压压气机转子和高压涡轮转子组合件简称高压转子组合件,高压转子组合不平衡量会引起发动机振动,发动机振动则会严重影响发动机的性能。特别是在飞行过程中,发动机振动会增大磨损,导致系统故障,造成不可预知的后果[1]。付玄等[2]分析振动组件的动态响应特性,将高频轴向振动应用于相应螺母的分解操作。陈果[3]建立了含复杂滚动轴承的航空发动机振动模型,并进行了研究。栗江等[4]研究连接结构对航空发动机装配体振动特性的影响,有助于实现对航空发动机振动特性的精确分析,提高航空发动机的整机性能。冯健朋等[5]介绍了航空发动机动平衡及振动不平衡相位检测技术的现状与发展。高金吉[6]指出航空发动机振动问题较为突出,是设计、研制、生产、使用新一代航空发动机的瓶颈。柏树生等[7]分析了航空发动机常见振动故障,提出了排除措施。孟俊[8]对航空发动机振动控制技术进行了分析和验证。任志远等[9]针对航空发动机振动故障,确认振动原因为低压涡轮转子不平衡,进而对低压涡轮转子平衡工艺进行优化,保证了低压涡轮转子的平衡质量,排除了振动故障。郑丽等[10]总结了航空发动机振动问题的研究现状和趋势,具有一定的参考价值。洪亮等[11]提出转子对中性差及螺栓连接松动是导致航空发动机压气机部件出现振动异常的原因。
发动机振动对发动机使用寿命影响很大,控制发动机振动是延长发动机使用寿命的重要手段。笔者针对高压转子组合不平衡量对发动机振动的影响进行分析。
2 高压转子组合不平衡量对发动机振动峰值的影响
2.1 理论分析
发动机振动的主要原因是高压转子组合件受到不平衡力作用。由于高压转子组合件的质心与形心不一致,使高压转子组合件出现质量不平衡,导致发动机振动峰值较大。根据发动机试车振动情况及发动机试车后高压转子组合件检查情况,确认发动机振动峰值较大是由高压转子组合不平衡量较大引起的。对于振动峰值较大的发动机,可以采用减小高压转子组合不平衡量的方法来应对。
高压转子组合件运动示意图如图1所示。设高压转子组合件的质量差为Δm,转速为ω,自旋转半径为r,偏离中心旋转半径为R,则高压转子组合件的不平衡力F为:
F=Δmω2r
(1)

图1 高压转子组合件运动示意图
发动机工作过程中,高压转子组合件会偏离中心做旋转运动,发动机存在振动。高压转子组合件偏离中心做旋转运动的线速度对应振动峰值时,高压转子组合件所受的不平衡力即为高压转子组合件的离心力F1:
F1=F=Δmω2r=mv2/R
(2)
式中:m为高压转子组合件的质量;v为发动机振动峰值。
由式(1)、式(2)可知,当高压转子组合不平衡量较小时,高压转子组合件的质量差较小,高压转子组合件受到的不平衡力和离心力较小,发动机振动峰值也较小;随着高压转子组合不平衡量增大,高压转子组合件的质量差增大,高压转子组合件受到的不平衡力和离心力增大,发动机振动峰值也增大。由此可见,可以通过控制高压转子组合不平衡量来控制发动机的振动峰值。
2.2 统计分析
发动机的振动峰值是评判发动机振动是否合格的重要参数之一。为分析高压转子组合不平衡量对发动机振动峰值的影响,统计200台次发动机的高压转子组合不平衡量,分为小于10 g·cm、10~15 g·cm、15~20 g·cm、20~25 g·cm四个组别,分析不同组别高压转子组合不平衡量对发动机振动峰值的影响。
根据发动机设计文件要求判定发动机振动峰值是否合格,高压转子组合不平衡量对发动机振动峰值合格率的影响如图2所示。在高压转子组合不平衡量的四个组别中,发动机振动峰值的合格率均高于不合格率。高压转子组合不平衡量越小,发动机振动峰值的合格率越高,表征发动机振动峰值合格的可能性越大。

图2 高压转子组合不平衡量对发动机振动峰值合格率的影响
设置分界线用于判定发动机振动峰值是否优秀,高压转子组合不平衡量对发动机振动峰值优秀率的影响如图3所示。由图3可知,将高压转子组合不平衡量控制在15 g·cm以下,可以保证发动机振动峰值的优秀率高于非优秀率。高压转子组合不平衡量越小,发动机振动峰值优秀率越高,发动机振动峰值优秀的可能性越大。
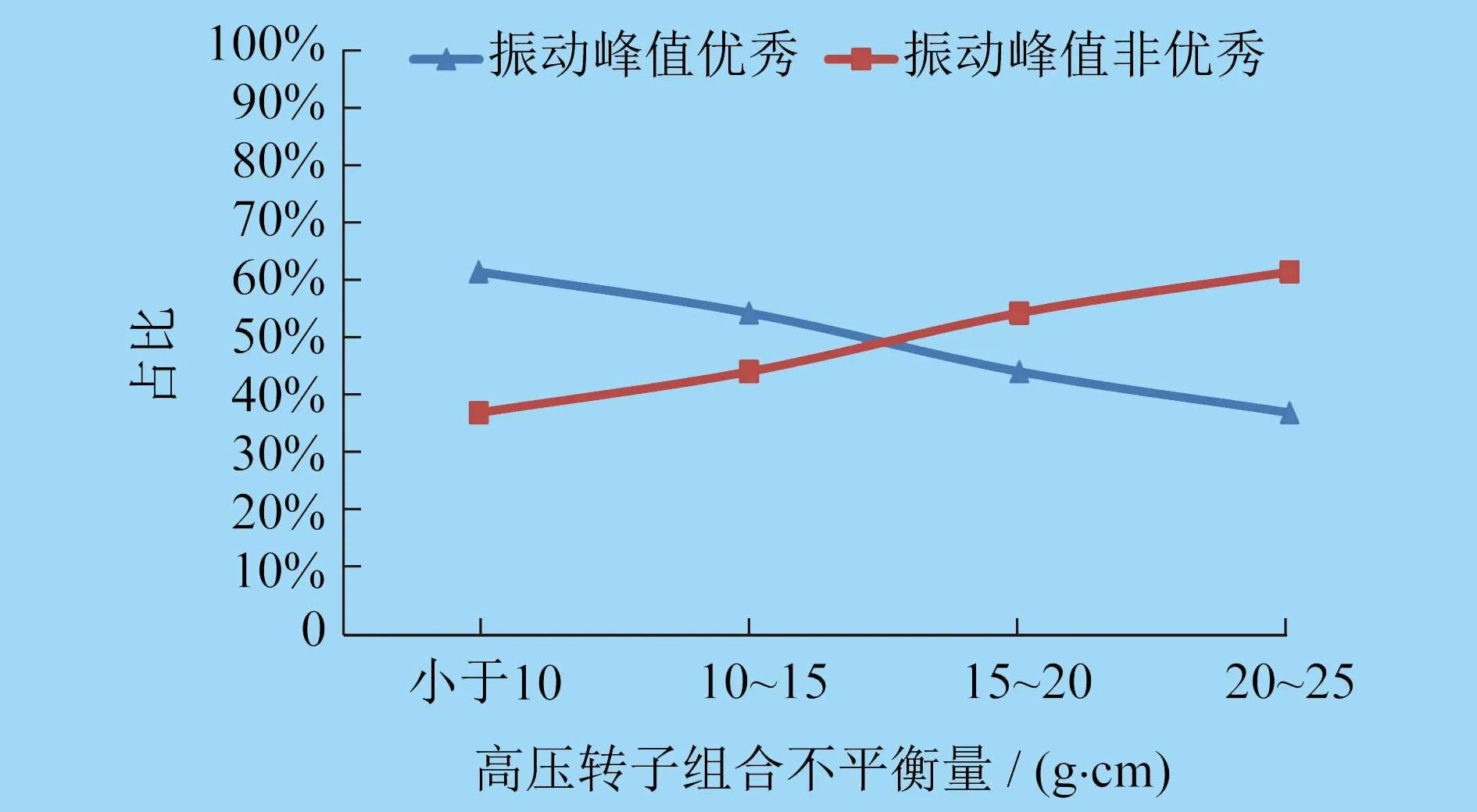
图3 高压转子组合不平衡量对发动机振动峰值优秀率的影响
3 高压转子组合不平衡量对发动机振动变化的影响
3.1 理论分析
高压转子组合件在工作过程中,受到不平衡力的作用,绕中心做旋转运动,不同运动位置如图4所示。根据能量守恒定律,有:
mv2/2=mgh
(3)
式中:h为高压转子组合件的摆动幅度;g为重力加速度。
(1) 当高压转子组合不平衡量较小时,高压转子组合件的质量差较小,根据式(1)、式(2)可以判定高压转子组合件所受的离心力较小,发动机振动峰值较小,于是根据式(3)有:
mv2/2=mgh1<2mgR
(4)
式中:h1为高压转子组合件的摆动高度。
此时对应位置一,h1小于2R,高压转子组合件无法绕轴线做圆周运动,发动机的振动峰值和振动变化均较小。
(2) 当高压转子组合不平衡量增大时,高压转子组合件的质量差增大,根据式(1)、式(2)可以判定高压转子组合件所受的离心力增大,发动机振动峰值增大,于是根据式(3)有:
mv2/2=mgh2<2mgR
(5)
式中:h2为高压转子组合件的摆动高度。
此时对应位置二,h2小于2R,高压转子组合件无法绕轴线做圆周运动,但发动机的振动峰值和振动变化值均增大。

图4 高压转子组合件运动位置
(3) 当高压转子组合不平衡量继续增大时,高压转子组合件的质量差很大,根据式(1)、式(2)可以判定高压转子组合件所受的离心力很大,发动机振动峰值很大,于是根据式(3)有:
mv2/2>2mgR
(6)
此时对应位置三,高压转子组合件可以绕轴线做圆周运动,发动机的振动峰值很大,振动变化则为零。
3.2 统计分析
发动机在同一转速下,振动峰值的变化量称为发动机振动变化值,发动机振动变化值是评判发动机振动合格的另一个重要参数。为分析高压转子组合不平衡量对发动机振动变化的影响,统计200台次发动机高压转子组合不平衡值,共分为小于10 g·cm、10~15 g·cm、15~20 g·cm、20~25 g·cm四个组别。
根据发动机设计文件要求判定发动机振动变化是否合格,高压转子组合不平衡量对发动机振动变化合格率的影响如图5所示。由图5可知,在高压转子组合不平衡量四个组别中,发动机振动变化的合格率均远高于不合格率。高压转子组合不平衡量控制在10 g·cm以下或20~25 g·cm时,发动机振动变化合格率较高。

图5 高压转子组合不平衡量对发动机振动变化合格率的影响
设置分界线用于判定发动机振动变化是否优秀,高压转子组合不平衡量对发动机振动变化优秀率的影响如图6所示。由图6可知,在划分的高压转子组合不平衡量的四个组别中,小于10 g·cm、15~20 g·cm两个组别的发动机振动变化优秀率较高,尤其是高压转子组合不平衡量小于10 g·cm时,发动机振动变化的优秀率最高。
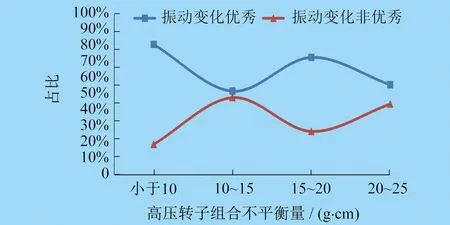
图6 高压转子组合不平衡量对发动机振动变化优秀率的影响
4 分析结论
(1) 高压转子组合不平衡量越小,发动机振动峰值合格的可能性越大,发动机振动峰值优秀的可能性越大,因此,高压转子组合不平衡量越小越好。
(2) 高压转子组合不平衡量控制在10 g·cm以下或20 g~25 g·cm时,发动机振动变化合格率及优秀率较高。
(3) 综合考虑发动机振动峰值和振动变化,建议将高压转子组合不平衡量控制在10 g·cm以下。

