基于VMD-TEO的输电线路故障定位方法

张文坚，申岩，于文斌

(哈尔滨工业大学 电气工程及其自动化学院，黑龙江 哈尔滨 150001)

随着我国电网容量、距离、规模的增大，各等级输电线路总长也在逐渐攀升。而大多架设在山区、江河以及环境恶劣地区的架空线路受到线路故障影响将更加严重，电网的安全运行稳定性将面临干扰[1]。故障持续时间的长短决定了对电网产生危害的大小，快速准确定位故障点是输电线路安全运行的一项重大要求。

目前国内外对线路故障测距方面的研究日趋成熟，故障分析法以及行波法已经大量运用在实际工作场合中。尤为突出的是行波法中的双端行波法，即D型行波定位方法，其原理较单端行波法更加可靠，并且行波衰减现象更少见[2-3]。但在行波波头的检测领域中，仍存在一系列问题[4]。

针对行波波头的准确检测，有学者提出了基于小波变换理论提取故障行波波头，该方法利用小波分解后的某一尺度来提取模极大值，作为行波波头到达时刻带入计算[5-9]。小波变换不失为一种有效的波头提取方法，不过由于方法的自适应性差，小波基函数种类和不同分解尺度将会给计算结果带来较大差异，若行波信号中含有噪声干扰，小波变换方法将失去良好的定位性能，甚至无法定位[10-11]。

本文提出利用变分模态分解(variational mode decomposition，VMD)算法来提取故障行波的波头信号，对于含有噪声较严重的信号，使用VMD算法分解行波故障信号[11-13]，然后通过Teager能量算子(Teager energy operator，TEO)对分解后的高频模态分量进行能量突变点的提取，得到对应行波到达时刻[14-16]。在交流输电线路故障测距背景下，VMD-TEO算法能通过分解后的低、中频段故障信息来提取波头到达时刻，有效避免了在高频段混叠噪声情况下的波头提取问题。利用分布式监测故障定位测距公式计算故障点位置[17-19]，并与仿真故障设置点对比得到误差距离。最后通过算例仿真，在含有噪声干扰的行波信号中利用VMD-TEO算法检测波头信号，与相同环境下的小波算法检测结果进行对比，以验证VMD-TEO算法的准确性。

1 算法理论

1.1 VMD算法原理

VMD算法是在经验模态分解(empirical mode decomposition，EMD)算法的基础上进行优化的一种分解算法。算法将信号分解成指定的层数，在不同的限带宽本征模态函数(band limited intrinsic mode function，BLIMF)分量中迭代求取模型的最优解，求取各个模态的中心频率与带宽，使得信号能够有效地自适应分解。

将信号f分解成K个模态分量uk(t)(k=1，2，…，K，其中t为时间)，各模态分量的中心频率为ωk，具体分解过程如下：

a)通过Hilbert变换[20]获得每个模态信号解析后的单边际频谱；

b)将各模态频率变换至基频带上，并由单个混合指数来控制估计的中心频率exp(-jωkt)；

c)高斯平滑解调信号获取分量带宽。

目标函数写为：

(1)

式中：∂t()为Hilbert变换；δ(t)为单位脉冲信号。

目标函数求解：

a)利用Lagrange函数将约束问题非约束化，增广Lagrange函数

(2)

式中：α为二次惩罚因子，用于数据约束平衡；λ(t)为Lagrange乘子，用于增强约束性。

b)求解增广Lagrange函数的鞍点需利用交替方向乘子法，分解求解uk,n+1、ωk,n+1以及λn+1(下标n+1表示第n+1次迭代，下同)，在收敛域附近求得最优分解结果。

求解过程中需要逐步更新uk,n+1、ωk,n+1与λn+1。uk,n+1的表达式为

(3)

式中X为模态分量集合。

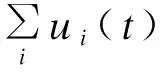
(4)

通过二次优化得到

(5)

此外，重构信号的表达式如果包含中心频率ωk，则表述为

(6)

优化可得

(7)

求解得

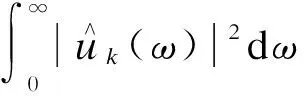
(8)

式(3)—(8)中：ω为原始信号的中心频率；顶标“∧”表示傅里叶变换。

Lagrange乘子更新公式为

(9)

式中τ为噪声容限参数，随着τ的降低可以增强对信号的过滤程度，τ=0时可过滤强噪声。

当迭代结果不满足停止条件，迭代将继续进行；当结果满足停止条件，即停止迭代，得到信号分解结果。停止条件为

(10)

式中ε为收敛条件。

1.2 VMD算法迭代流程

VMD算法交替迭代的流程如图1所示，首先初始化{uk,1}、{ωk,1}、λ1，依次通过式(5)、(8)、(9)迭代更新{uk,n+1}、{ωk,n+1}、{λn+1}，对每次迭代得到的{uk,n+1}、{ωk,n+1}、{λn+1}代入停止条件中判断结果，满足条件则停止迭代，不满足则继续下一次迭代，输出结果为经VMD算法自适应分解后的BLIMF分量。

图1 VMD算法交替迭代流程Fig.1 Alternative iteration process of VMD algorithm

1.3 TEO

卷积运算是Hilbert变换的实质，对模态分解后的信号x(t)进行Hilbert变换处理，可记为

(11)

构造解析信号z(t)，其表达式由变换前后的信号组成，即

(12)

瞬时频率

(13)

瞬时频率的极大值点与波头到达时刻相对应，但Hilbert变换中的卷积运算对信号的时间窗口较为敏感，时间窗口的长度、信号突变点等都是提取行波波头到达时刻的影响因素，直接关系到故障定位的精度。

本文使用TEO对故障行波信号波头进行检测，TEO与信号时窗长度及位置无关，具有运算量小、便捷的优势。

TEO处理连续信号x(t)的计算式为

ψ[x(t)]=x′2(t)-x(t)x″(t).

(14)

式中：ψ[]为TEO函数；x′(t)、x″(t)为信号的一阶与二阶导数。

TEO处理离散信号x(t)的计算式为

ψ[x(n)]=x2(n)-x(n+1)x(n-1).

(15)

通过TEO处理VMD分解后的信号，可以实现准确的信号能量跟踪，将提取到的能量极大值点作为故障行波波头到达时刻，从而进行故障定位运算。

2 线路模型与算法参数

2.1 系统模型

如图2所示，系统模型为全长100 km的110 kV交流线路。测点1、2、3间隔50 km安置在架空线路中。故障设置在测点1—测点2区间内。

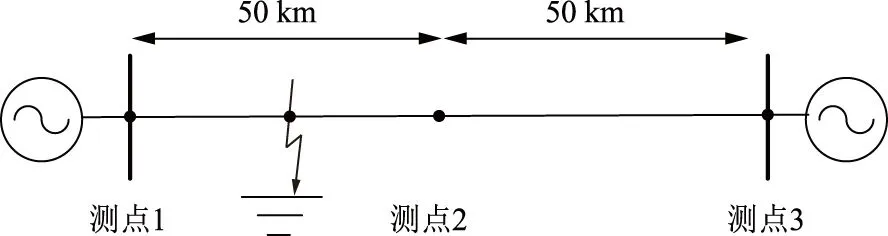
图2 110 kV输电线路仿真模型Fig.2 Simulation model of 110 kV transmission line

通过布置分布式监测点，可以实时在线测量波速，减小由波速不准确带来的定位误差，并且可以人为将监测点间的距离设定为较小值，进一步减小线路长度不确定性带来的误差。各监测点配置了GPS以及GPRS功能，GPS技术用来实现各个监测点间的对时同步，GPRS用来实现故障后行波数据的打包上传。

2.2 噪声模型

输电线路采集故障行波信号一般利用互感器，但互感器的检测易受噪声干扰。噪声的影响因素以及来源可以分为外部因素和内部因素。外部因素包括线路施工、电气设备干扰等；而内部因素一般来源于互感器自身内部的随机波动。

选取高斯白噪声作为噪声干扰项叠加在行波信号中，仿真噪声对波头检测的干扰，其中高斯白噪声的时域图像如图3所示。

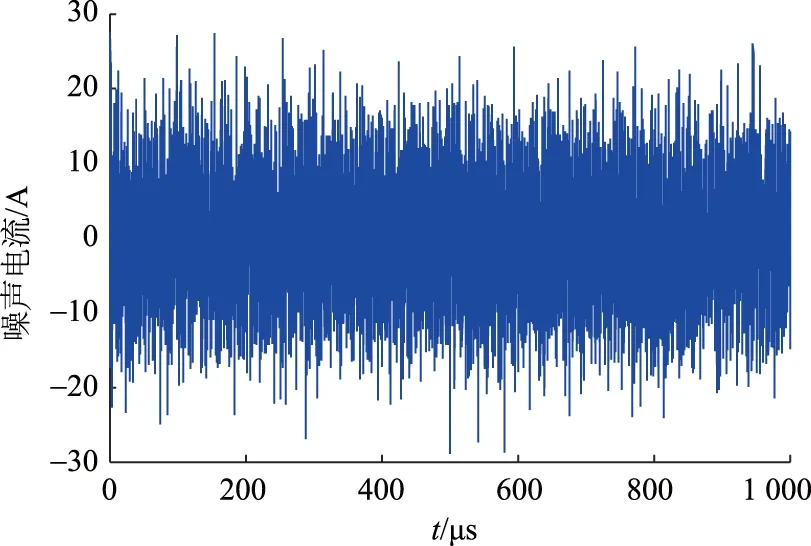
图3 高斯白噪声时域图像Fig.3 Time domain image of Gaussian white noise

2.3 算法参数选取

本文采用VMD-TEO算法对含噪行波进行滤波处理并提取行波波头到达时刻，设置分解模态数K=3,二次惩罚因子α=2 000。当K取值过大时，将出现过分解现象，故障信息将被淹没；当K取值很小时，不会出现过度分解问题，但是极值点的位置发生一定的偏移，将带来故障定位误差。当α取值很大时，模态极值在逐渐变小，存在被噪声干扰淹没的问题；当α取值很小时，极值点的位置和个数发生一定的偏移，影响故障定位准确度。通过大量算例分析，以上的VMD-TEO算法参数设置适用于处理各种电压等级线路的短路故障行波信号。当线路发生雷击故障时，分解模态数取K=4,定位效果更优。

3 仿真分析

本文通过ATP-EMTP仿真软件对110 kV电压等级交流架空输电线进行短路故障仿真，其中输电线路选择J.Marti频变参数模型，在线路测点1与测点2之间设置故障点位置距测点1为27 km，故障发生于0.3 ms时刻，仿真总时长设置为2 ms，并采用凯伦贝尔变换矩阵进行三相解耦计算。

幅值越小的行波信号越容易受到噪声的干扰，从而在波头检测环节出现到达时刻偏移或者误测的问题，导致故障定位存在较大误差，增加后续巡线工作负担。仿真设置采样频率10 MHz，故障角相同，过渡电阻分别为20 Ω、200 Ω、400 Ω时的短路故障，白噪声叠加在故障电流行波中的波形如图4所示。

图4 不同过渡电阻下的带噪故障行波波形Fig.4 Traveling waveforms of noise fault with different transition resistance

由于故障行波幅值与过渡电阻呈反比，在过渡电阻逐渐增加的过程中，原始行波单调奇异性特征逐渐消失于杂乱无章的白噪声中。对不同过渡电阻的行波信号分别进行db4小波分解，分解层数为6层(d1—d6)。其中过渡电阻为20 Ω的分解结果如图5所示，过渡电阻为400 Ω的分解结果如图6所示。

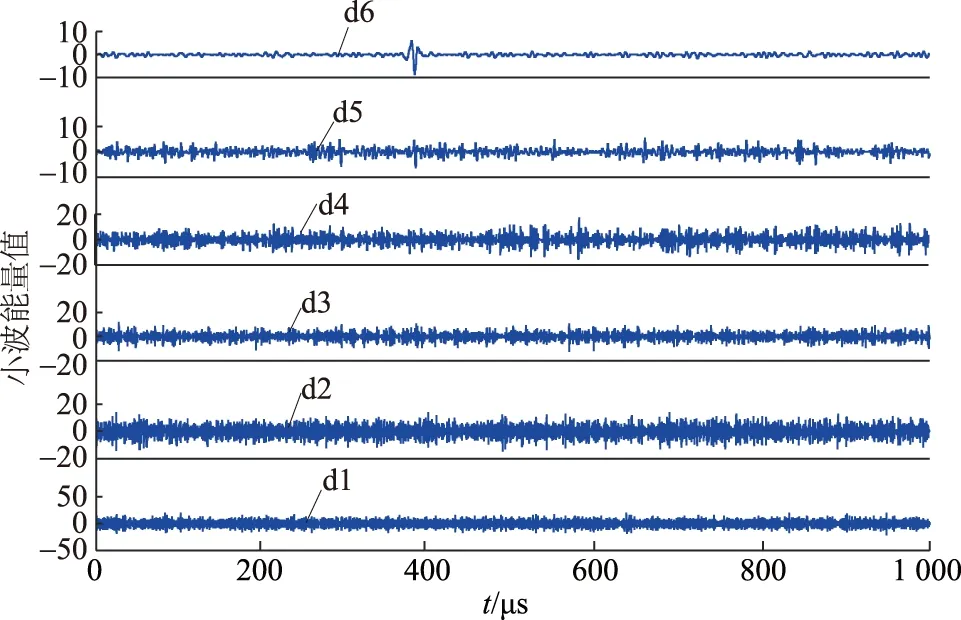
图5 过渡电阻为20 Ω时，带噪故障行波的小波分解结果Fig.5 Wavelet decomposition results of traveling wave with noise when the transition resistance is 20 Ω

图6 过渡电阻为400 Ω时，带噪故障行波的小波分解结果Fig.6 Wavelet decomposition results of traveling wave with noise when the transition resistance is 400 Ω

从图5可以看出，d1—d4层均呈现白噪声特征，噪声干扰随着小波分解层数的增加而略有减弱。对d6层一处幅值明显的模极大值进行到达时刻提取，可得t=386.3 μs。

从图6可以看出，行波幅值的下降导致d5层已经难以发现模极大值点，在最高层中提取波头到达时刻t=380.5 μs。将其与低层次的小波变换波头检测结果对比，发现随着故障行波自身幅值减小，行波信号受到噪声影响变大，在强噪声影响下，高分解尺度中才勉强能提取波头到达时刻，但仍存在时刻偏移问题。

分布式定位法利用每个监测点采集的第一个行波波头到达时刻来计算故障发生位置，对同相角、过渡电阻分别为20 Ω、200 Ω、400 Ω时的带噪故障行波信号均利用小波变换提取首波头达到时刻，计算故障点位置以及定位误差，结果见表1。

表1 不同过渡电阻时，利用小波变换法处理带噪故障行波的测距结果Tab.1 Distance measurement results of traveling wave with noise using wavelet transform method under different transition resistances

由表1可知，小波变换处理含噪故障行波来提取波头到达时刻，分解后的高频分量仍含有大量噪声干扰，波形呈白噪声状。而利用低频段的小波分量来提取波头到达时刻将会产生时刻的偏移，造成较大的定位误差。当过渡电阻达到400 Ω时，分布式故障定位结果与真实值相差873 m，这已经远超过采样率为10 MHz的误差阈值，说明噪声环境下小波变换法检测行波到达时刻的定位准确度较一般。

由上述结论可知，当故障的过渡电阻为400 Ω时，小波变换法的测距误差为873 m，定位精度较一般。利用VMD算法对相同噪声背景下﹝图4(c)﹞的故障行波进行分解，将信号分解为高、中、低3个频段，分解结果如图7所示。

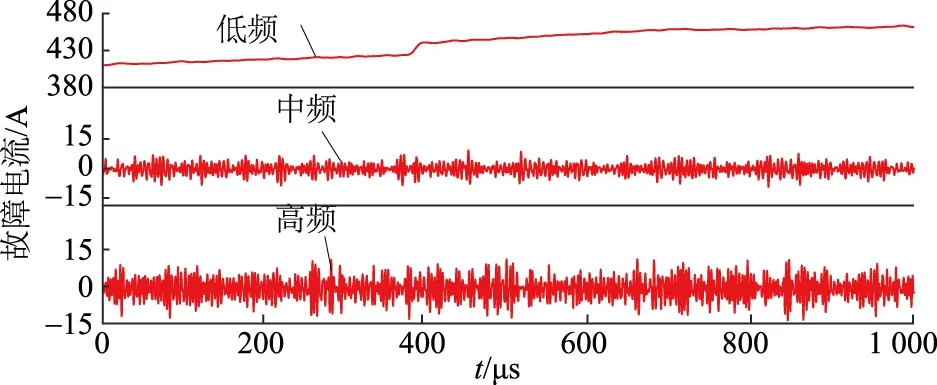
图7 经VMD算法分解后的带噪故障信号Fig.7 Noisy signals after VMD decomposition

经VMD算法分解后的带噪信号与小波分解结果类似，高频段仍存在白噪声特征，而低频段却很好地保留了原始行波特征。将经VMD算法处理后的低频段信号波形与无噪的原始故障行波信号进行对比，如图8所示。

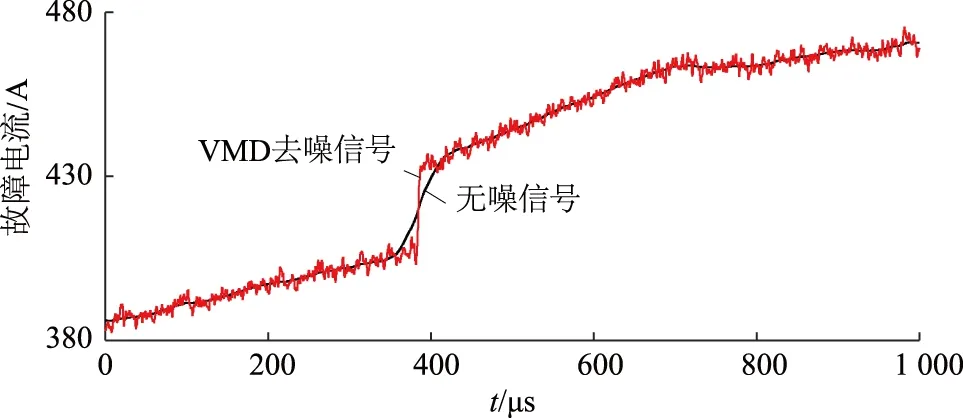
图8 经VMD算法分解后的低频信号与原始信号对比Fig.8 Comparison between low-frequency signal and original signal after VMD decomposition

由图8可以看出，VMD算法能够对含噪信号作一次降噪处理，过滤掉大部分噪声，并恢复故障信号的原始波形特性。对最低频的BLIMF分量再进行VMD算法分解，分解结果如图9所示。

对首次VMD算法分解后得到的最低频信号分量进行二次VMD算法分解，相当于二次滤波，从二次分解图中可以看出最高频仍然呈现较无序的噪声特征，观察中频段信号波形发现有明显的极大值点，说明带噪信号经过二次VMD分解可以提取到行波到达监测点时刻。通过TEO提取信号瞬时能量变化的极大值点，提取对应的横坐标。3个测点的结果如图10所示。

图9 低频信号二次VMD算法分解结果Fig.9 Results of low-frequency signals after secondary VMD decomposition

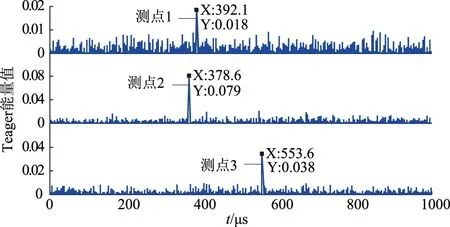
图10 3个测点带噪信号波头检测结果Fig.10 Detection results of noisy signal wavefronts at three detection points

得到3个测点的故障行波到达时刻分别为t1=392.1 μs、t2=378.6 μs、t3=553.6 μs。代入定位公式可得

(16)

式中：x为故障距离测点1的距离；v为行波波速；L12为测点1与测点2的距离；L23为测点2与测点3的距离。

计算结果与仿真原始故障定位误差仅有74 m，远小于利用小波变换处理信号时的测距误差。

为更好地说明算法的适用性，改变故障位置以及过渡电阻值的大小，计算小波变换与VMD-TEO算法的故障定位结果，见表2。

表2 不同故障位置时，小波变换法与VMD-TEO算法的故障定位结果Tab.2 Fault location results based on wavelet transform method and VMD-TEO algorithm for different faults

由表2可知，在高功率噪声干扰环境下或低幅值故障行波信号的情况下，VMD-TEO算法仍可以有效提取行波波头到达时刻并得到较为准确的故障位置，定位误差小于0.1%。对于带噪行波信号的波头检测问题，VMD-TEO算法在噪声环境下的定位效果优于传统小波变换法。

4 结束语

针对传统小波变换法在短路行波故障存在噪声干扰情况下检测行波波头自适应性差、定位精度低的问题，本文基于VMD-TEO算法对故障行波进行噪声过滤与自适应分解，结合分布式监测的故障定位理论，使得故障波形更具真实度，定位误差不足0.1%。本文方法完全可以用于输电线路短路故障定位测距。