钢桁架拱桥施工阶段风荷载计算及稳定性分析
姜 敏
(中铁第五勘察设计院集团有限公司,北京 102600)
1 前 言
随着我国交通网路系统的完善,桥梁跨度不断增长,桥梁的柔度逐渐增大,桥梁逐渐成为风致振动敏感结构。桥梁施工阶段与成桥状态相比较时,由于施工阶段结构的最终体系尚未形成,结构的柔度较大,尤其是在主梁架设初期,结构的抗风稳定性与成桥状态相比较差,风作用对桥梁施工阶段的影响更为突出,因此对桥梁施工阶段进行抗风稳定性分析很有必要。抗风稳定性校核计算有静力校核计算和动力校核计算之分,静力校核计算是以一定的设计风速为依据来计算作用于桥梁结构上的风荷载,按照静力学的校核计算方法来验算结构在该风速作用下是否安全。对于大跨度钢桁拱桥而言,这就要求我们准确掌握多榀桁架梁的风荷载计算方法,本文针对大跨度三榀桁架桥的风荷载进行了研究。
2 工程概况
本文以广州市南沙区在建明珠湾大跨度连续钢桁架拱桥为依托,确定相关规范关于风荷载参数的计算方法。其主桥采用(96+164+436+164+96+60)m中承式六跨连续钢桁拱桥,全长1 016 m。据当地2004~2017年风向、风速资料统计,该地区春、东两季以N、NNE、NE风向为主;夏、秋两季以S风向为主,历年最大风速26 m/s。本区为台风影响区,台风一般发生在6~10月,年均受影响的次数2.85次,最大风力在9级以上。由于工程建设需要,施工期不能避开台风期。故施工阶段的抗风评估及抗风措施将直接影响施工的安全与质量。
此桥主梁为三主桁连续钢桁拱桥结构,桁间距18.1 m,边桁桁高10.369 m,中桁桁高10.685 m,边桁拱顶至中墩支点高度为109 m,拱肋下弦线形采用二次抛物线,其矢高98 m,矢跨比为1/4.45。桥型布置图见图1,横断面布置见图2。

图1 桥型布置图
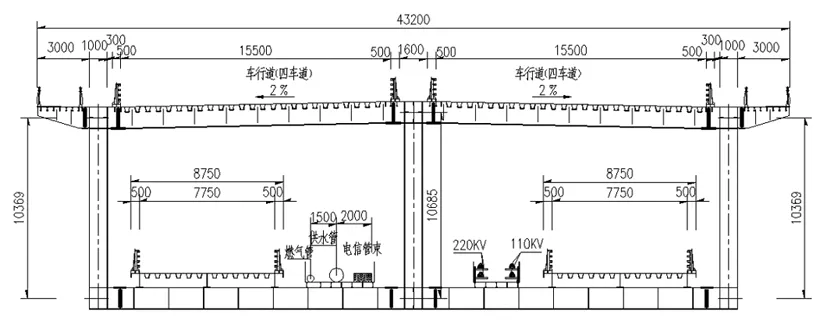
图2 横断面图/mm
以主梁一节段为例,按规范要求计算其风荷载取值。全桥基本节间距为 12 m,在主墩顶拱脚处部分区段采用 14 m节间。主桁杆件高度为1.2 m,杆件最大板厚52 mm,腹杆截面最大高度为1.2 m,内宽1 m,最大板厚为56 mm。12 m节间桁架净面积A1=(1.2+0.052)×12×2+(1+0.056)×10.685+1×(10.6852+122)0.5=57.4 m2;12 m节间桁架轮廓面积A2=(1.2+0.052+10.685)×12=143.2 m2。实面积比=桁架净面积/桁架轮廓面积=A1/A2=0.4,间距比=两桁架中心距/迎风桁架高度=18.1/10.685=1.69。由于此桥位于开阔水面,故地表类别为A类。
3 风荷载标准值计算
3.1 按《公路桥梁抗风设计规范》计算
根据《公路桥梁抗风设计规范》(JTG∕T 3360-01-2018)可知,由实面积比与间距比可得桁架遮挡系数η=0.635,上部结构为两片或两片以上桁架时,每片桁架的横向力系数均取为ηCH。
根据《公路桥梁抗风设计规范》(JTG∕T 3360-01-2018),风荷载计算如下:
桥梁或构件基准高度Z处的设计基准风速
Usd=ksfkfktkhU10=0.88×1.05×1×1.37×37.6=47.6 m/s
(1)
式中:Ud为桥梁或构件基准高度Z处的设计基准风速,m/s;ksf为施工阶段抗风风险系数;kf为抗风风险系数;kt为地形条件系数;kh为地表类别转换及风速高度修正系数。
等效静阵风风速
Ug=GvUd=1.22×47.6=59 m/s
(2)
式中:Gv为等效静阵风系数。
横桥向风作用下主梁每片桁架单位长度上的顺风向等效静阵风荷载:
Fg=1/2ρUg2ηCHD=1/2×1.25×592×0.635×1×0.4×10.685=5 904.6 N/m
(3)
式中:Fg为作用在主梁单位长度上的顺风向等效静阵风荷载,N/m;ρ为空气密度, kg/m3,可取为1.25 kg/m3;Ug为等效静阵风风速,m/s;CH为主梁横向力系数;D为主梁特征高度,m。
3.2 按《建筑结构荷载规范》计算
计算主要受力结构时,风荷载标准值
wk=βzμsμzw0
(4)
式中:βz为高度z处的风振系数;μs为风荷载体型系数;μz为风压高度变化系数;w0为基本风压,KN/m2,w0=1/2ρv02=1/2×1.25×10-3×37.62=0.883 6 KN/m2v0为基本风速;ρ为空气密度。
根据《建筑结构荷载规范》8.4.1条可知对于高度大于30 m且高宽比大于1.5倍的房屋,以及基本自振周期T1大于0.25 s的各种高耸结构,应考虑风压脉动对结构产生风向风振的影响。对于此桥可不考虑脉动风振作用,故高度z处的风振系数βz=1。
根据表8.2.1可得地面粗糙度A类,离地面或海平面高度为36 m,风压高度变化系数为1.742。
对于n片型式相同且彼此等间隔的等高结构,应考虑多片结构的重叠挡风折减作用。根据表8.3.1可得:n榀平行桁架的整体体型系数μstw=μst(1-ηn)/(1-η),式中μst为单榀桁架的体型系数,μst=φμs。μs为桁架构件的体型系数,φ=An/A为桁架的挡风系数,An为挡风净投影面积,A为桁架的轮廓面积。
三榀平行桁架的风荷载体型系数μstw=μst(1-η3)/(1-η)=0.4×1.3×(1-0.5693)/(1-0.569)=0.984。
故按《建筑结构荷载规范》可得三片主桁整体风荷载标准值wk=βzμsμzw0=1×0.984×1.742×0.883 6=1.515 KN/m2。
根据《建筑结构荷载规范》可得风荷载作用在三片桁架单位长度上的顺风向风荷载F=wkA2/12=1.515×143.2/12=18.079 KN/m。
3.3 风荷载标准值计算结果差异分析
从上述两种不同规范关于风荷载的计算结果可知,风荷载标准值“公路桥梁抗风设计规范”/“建筑结构荷载规范”=3×5.9/18.079=0.98,其中《公路桥梁抗风设计规范》考虑了抗风风险系数ksf=0.88及kf=1.05;若不考虑,风荷载标准值“公路桥梁抗风设计规范”/“建筑结构荷载规范”=3×5.9/(0.88×1.05)/18.079=1.06。两种规范的计算结果相差不大。两种规范计算过程中具体参数差异详见表1。

表1 计算参数类比
4 施工阶段的稳定性分析
采用MIDAS Civil2019有限元分析软件对在建明珠湾大跨度连续钢桁架拱桥进行施工过程分析,采用梁单元和桁架单元建立三维模型,节点共4 455个,单元共11 148个。施工阶段整体有限元模型见图3。

图3 明珠湾大桥有限元模型
桥梁的静态失稳可以分为两种形式:横向屈曲和静态扭转发散。通常指桥梁结构在一定风速作用下,产生弯曲或扭转变形,一方面桥梁结构的变形会改变其刚度,另一方面会影响风场分布,从而改变风的大小和方向,反过来它进一步增大了结构的变形,最终导致结构失稳的现象。
本文为施工阶段分析,考虑的荷载为结构自重、施工荷载(吊机、压重等)及风荷载。其中风荷载取值采用《公路桥梁抗风设计规范》计算值。通过分析,随着施工过程中主梁跨度的增大,结构整体柔度逐渐增大,故桥梁结构最大单悬臂状态的静风稳定性最差,跨中合拢前大悬臂状态为控制工况。在MIDAS Civil的屈曲分析中,提取组合工况下稳定安全系数,对失稳模型进行分析。

图4 小里程侧桥塔扭转整体屈曲
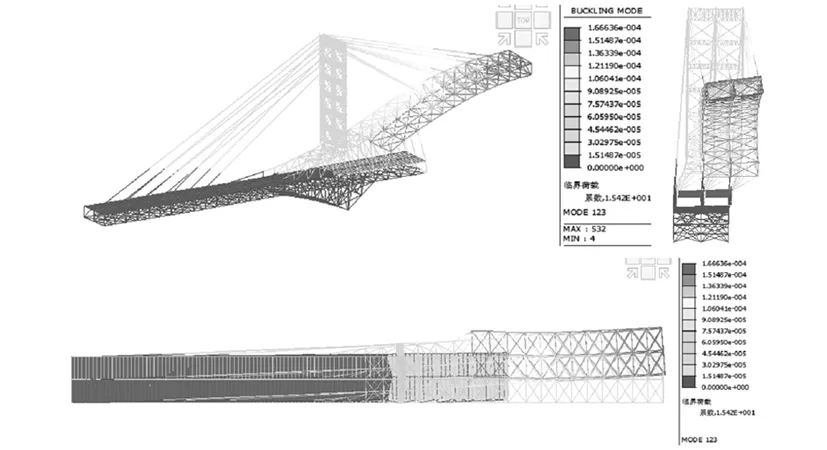
图5 小里程侧侧向整体屈曲
由计算结果可知,在组合荷载工况下,此桥三主桁钢桁梁的整体弹性稳定安全系数值最小为11.5,满足《公路斜拉桥设计规范》(试行)(JTJ027-96)中规定的结构稳定安全系数应大于4的要求。
5 结 语
(1)《公路桥梁抗风设计规范》采用的基本风速U10为重现期100年的风速数学期望值,而《建筑结构荷载规范》采用的是重现期50年的风压值,“建筑结构荷载规范”规定对于高层建筑、高耸结构及对风荷载比较敏感的其他结构,基本风压的取值应适当提高。
(2)对于钢桁架桥风荷载标准值而言,上述两种规范风荷载的计算结果相差2%~6%,结果基本吻合。
(3)对于自振周期较大、跨径较大或者对风荷载敏感的结构,应考虑脉动风荷载的影响。桥梁结构建议参考《公路桥梁抗风设计规范》根据地表类别和风荷载水平加载长度考虑阵风系数的影响。
(4)通过模型计算的明珠湾钢桁梁最大单悬臂状态抗风整体稳定性虽满足规范要求,但由于风本身的复杂性使得结构的风致振动是一个复杂的变化过程,关系到施工过程中结构的抗风安全问题。故施工过程中可采取一定的抗风措施来保证施工过程的安全,建议措施有以下几种。
在最大单悬臂阶段为防止发生围绕桥塔平面外的水平摆动以及平面内的竖向振动,建议悬臂施工应避免强风季节,尽快完成边跨合龙,必要时可设置临时墩来缩短悬臂长度;在最大单悬臂阶段,强风作用下主梁的平面外和平面内抖振产生的惯性力较大,根据实际情况,必要时可设置阻尼器及临时风缆来抑制振动。
若施工过程中斜拉索有足够大的阻尼,便不会发生尾流驰振和风雨共振。因此,提高阻尼可在斜拉索与主梁交接处附近安装油压阻尼器或粘性剪切型阻尼器来降低尾流驰振和风雨共振产生的不利影响。

