基于SEM的PPP项目政府补偿决策影响因素研究

朱琛，申建红，2，贾格淋，王迪

(1.青岛理工大学 管理工程学院，山东 青岛 266520；2. 山东省高校智慧城市建设管理研究中心，山东 青岛 266520)

PPP(Public—Private—Partnership)是指政府采取补偿措施激励社会资本融入资金，投资建设基础设施项目的一种优化的融资方式，能够减轻政府在财政收支方面的负担，避免不必要的费用超支，从而达到降低风险，互利共赢的局面[1]。但由于PPP项目多集中在公共产品或城市基础设施领域，受限于自身的准公共物品属性，前期投入多，如果后期运营不足，就会导致未来现金流很难补偿所有的投资成本，而适当合理的政府补偿决策不仅能保证社会资本方的权益，有效地激励社会资本的投入，还能够提高项目的运行效率。因此，研究政府补偿决策的影响因素对于PPP项目的成功运营具有十分重要的意义。

PPP项目具有准公益性，而社会资本方在考虑资金投入项目时，往往考虑的是投资成本的利益最大化，因此政府作出的补偿决策对于社会资本方资金的投入具有极大的吸引力。国内外已有不少学者对PPP项目政府补偿决策进行研究。Zhenyao Wu，Bin Shuai针对公路PPP项目建立了税收补贴模型和交通补贴模型，采用蒙特卡洛模拟方法得到不同补偿方式下政府补贴的价值和可能性，为政府选择合理的补贴方式、平衡补偿风险、制定补贴政策等提供有益参考[2]。Xiaowei An等考虑城市水环境治理的经济效益，采用博弈论方法求解激励系数，基于此建立了一种有效的政府补偿决策，为城市水环境治理PPP项目的实施提供参考[3]。王春艳，朱炜认为收益状态会影响政府作出合理的补偿决策，基于收益动态平衡的原则，预测项目的收入界限并构建合理的政府补偿机制，研究项目收益与政府补偿存在的关系[4]。袁汝华等将净收益法引入水利PPP项目政府补贴模型，采用当地价格取代协议价格对补贴额进行改进，并选取了172个水利工程实例验证模型的可行性[5]。还有学者将偏好理论引入政府补偿机制中，从补偿契约视角下研究政府补偿机制并建立相关模型，高华，张璇认为社会资本公平偏好的程度会影响政府作出补偿决策，将公平偏好理论引入政府补偿机制的研究中，运用Stackelberg博弈方法探讨公平偏好下社会资本的投资决策与政府补偿机制的关系[6]。杜洋，丰景春从公私两方风险偏好差异的角度，分别建立了政府和社会资本方的期望效用函数，基于此对政府和社会资本方的投资策略进行博弈，改进政府补偿决策的方法，得出了政府在集中决策与分散决策下的最优补偿方案[7]。吴孝灵等从政府补偿契约角度出发，基于改进FS模型建立了政府补偿下的投资决策模型[8]。张硕宇，任志涛通过讨价还价模型建立了不完全契约视角下的政府补偿机制[9]。综上所述，国内外学者对PPP项目政府补偿研究主要集中在对政府补偿决策建立相关模型以及政府补偿机制的研究上，很少有对政府补偿决策影响因素及其关系之间的研究，事实上政府作出补偿决策受到多种因素的影响。

本文首先利用文献统计分析法对影响政府作出补偿的因素进行识别并采用专家打分法进行初步筛选；其次通过问卷调查和灰色关联度对相关指标进行确定，构建政府补偿决策影响因素结构方程模型，最后运用数学的方法对工程项目、政府承受能力、社会资本方、社会公众和外部环境五项潜在因素对政府补偿决策的影响程度进行权重计算，以期为政府作出补偿决策提供相关依据。

1 政府补偿决策因素识别和确定

1.1 政府补偿决策因素的识别

为了科学有效地识别政府补偿决策的影响因素，通过在中国知网上检索“政府补偿”“PPP项目”“补偿决策”等关键词，限制时间搜索范围为2010～2020年，共筛选出210篇相关文献，根据这些文章中涉及到的决策因素，以citespace软件为构建工具，结合词频分析法，共确定了36个决策因素。将文献中提及的因素进行归纳划分，对其表意相似的因素进行整合处理，得到以下23个影响因素。按照工程项目、政府承受能力、社会资本方、社会公众、外部环境5个方面对主要因素进行归纳划分，如表1所示。

表1 政府补偿决策影响因素文献清单

1.2 政府补偿决策影响因素的确定

为了准确获得政府补偿决策因素及其重要程度，采用灰色关联度分析对各子因素之间的数值关系进行分析，并根据各因素之间关联度的大小进行指标筛选。为了增强数据的可信度和科学性，邀请20位具有PPP项目经验的专家组成评价小组，并向其发放“政府补偿决策影响因素咨询问卷”，对23个影响因素重要程度打分，调查专家的来源分布如表2所示。

表2 专家来源分布表

针对收集的23个评价项的数据资料，使用SPSSAU软件(分辨系数取0.5) 进行灰色关联度分析。根据灰色关联分析的原理，关联度越大，说明两个因素关系密切，相关程度越高；关联度越小，说明两个因素之间关系越弱[10-11]。以关联度大于 0.5 为入选标准，关联度统计结果如表3所示。由表3可以看出，C3、E1、E2 这3个评价项的关联度低于0.5，予以剔除，剩余的20个指标作为政府补偿决策影响因素的评价指标，如图1所示。

表3 关联度统计结果表

2 数据来源及分析

2.1 数据来源

将图1中影响政府作出补偿决策的20个因素作为问卷基础，另行设计“结构方程模型政府补偿影响因素量表”问卷,指标打分表采用李科特5级量表设计方法，根据每个因素的重要程度分为五级，其级别和分值如表4所示，受测者可根据个人经验进行打分。

调查问卷从2020年6月初开始发放，历时4个月，主要通过与PPP咨询公司交流访谈，进入企业公司、参加PPP交流会议等方式直接发放调查问卷，或对针对性人群发布线上调查问卷的方式进行填写。本次共发放了240份问卷，其中包含182份线下调查问卷，58份线上问卷，最终收回了213份，其中包含191份有效问卷，有效回收率为89.67%，达到了回收标准。对213份问卷进行调查对象基本资料的收集和整理，结果如表5所示。

表5 调查对象社会背景清单表

2.2 信度效度分析

信效度分析可以检验样本数据与真实结果的接近程度，利用 SPSS 26.0软件对数据进行可靠度分析。信度分析结果显示Cronbach's α为0.903，接近1，测量条款设计良好,信度较高；KMO值能够检验数据是否可以做因子分析，反映变量值之间的相关程度，大于0.7就可以反映变量之间的强关联性，如表6所示，效度分析中KMO值为0.869，较适合做因子分析；Bartlett球形检验主要检验数据的分布以及变量的独立性，P值小于0.05，则排斥原假设，表中显著性概率P值为0.000，说明问卷有效性高，统计量显著。问卷整体信度可靠，五个潜在变量的Cronbach's α信度系数均大于 0.6，在可接受范围内，因此具有较高的一致性和可靠性。

表6 SPSS效度分析表

3 结构方程模型及构建分析

3.1 结构方程模型

结构方程模型(Structural Equation Modeling,SEM )作为一种有效的多元数据统计分析工具，由测量模型和结构模型构成[12]。测量模型中有两个模型变量，一个是无法进行直接测量和观测的抽象变量——潜变量，另一个是对这些潜变量进行定量化描述的显变量，通常至少有两个变量因素，因此测量模型主要研究潜变量与显变量之间的关系；结构模型研究的是所有变量之间的关系，包括可以解释的部分以及无法用语言描述的部分，测量模型和结构模型两者的结合能够准确的测量整体模型的拟合程度[13]。

通过对2.1中的调查问卷收集的数据进行量化处理，运用结构方程模型进行验证性分析，确定影响因素之间的结构关系并利用路径系数判断关键指标。

3.2 一阶结构方程模型构建及分析

在AMOS22.0中将收集整理的数据导入，构建政府补偿决策影响因素模型如图2所示，根据模型的拟合情况发现，一阶模型中的参数，包括负误差项α，标准化系数k和误差项θ都在可接受范围内，通过违规估计检查，得到拟合结果，如表7所示。

卡方λ自由度比在1～3范围内显著性明显，通过表7得到，卡方λ自由度比为2.1，数据比较理想；GFI=0.926>9,CFI=0.987>0.9,IFI=0.964>0.9,TLI=0.953>0.9,近似均方差RMSEA=0.056<0.08,AGFI>0.9,表明该模型指标配适度良好，模型构建合理。

表7 AMOS拟合情况表

3.3 二阶结构方程模型建立及分析

3.2节中由于一阶模型具有较好的拟合度，同时发现五个一级指标之间的相关性呈大致相近关系，故利用二阶模型应能充分表达一阶因子关系。为准确判断政府补偿决策的关键影响，将二阶因子归集为政府补偿决策影响因素，用AMOS软件对数据重新处理，构建基于政府补偿决策影响因素的二阶SEM模型，运行结果如图3和表8所示。

表8 AMOS拟合情况表

通过表8得知，各个适配指标均在可接受范围内，拟合程度较高，说明理论模型接近实际数据，可靠性比较高。为了进一步反映政府补偿决策影响因素的指标的重要程度，根据路径系数对潜因素以及影响因素进行权重计算，结果如表9所示。

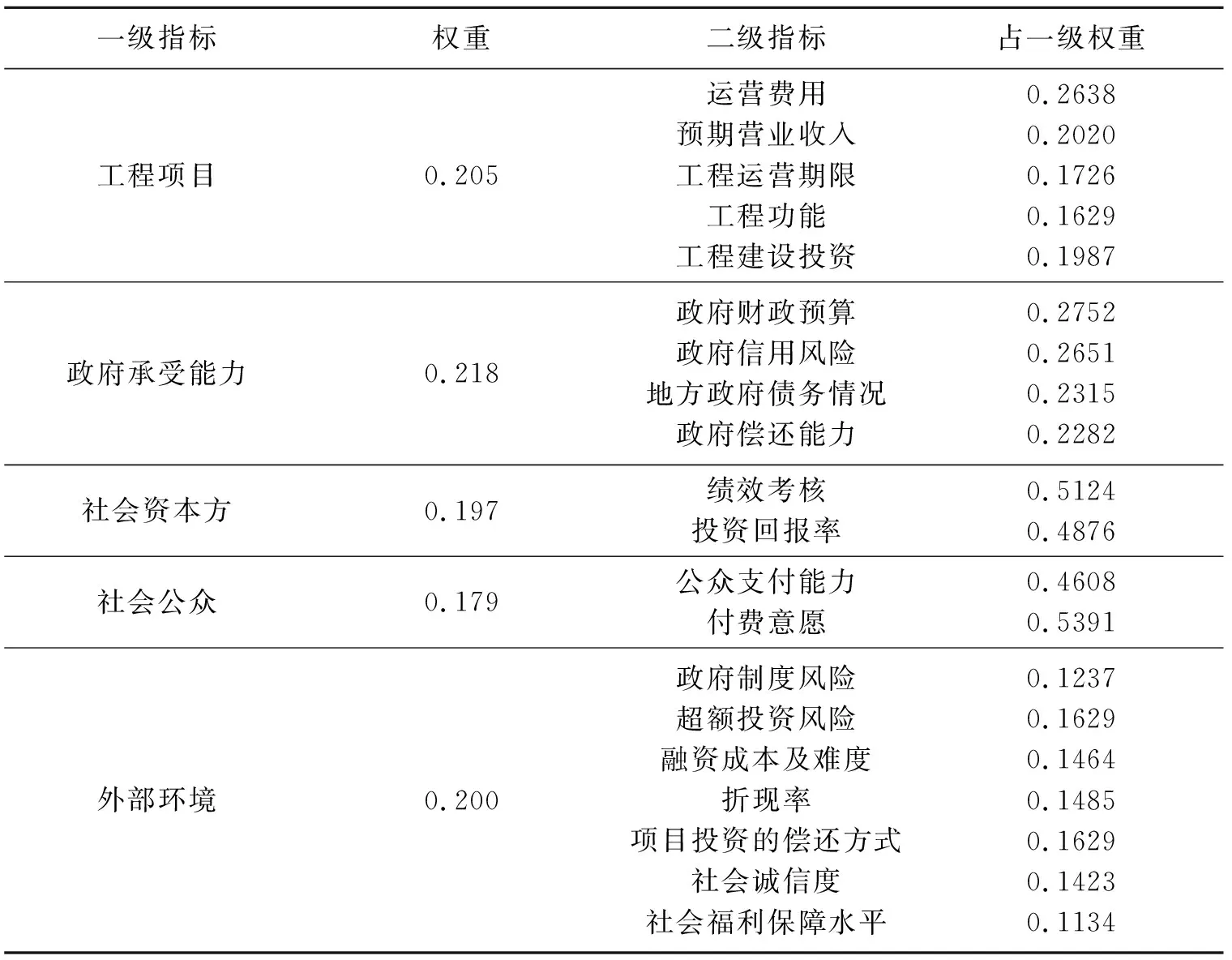
表9 权重计算表

3.4 解释结构方程模型

在PPP项目中影响政府补偿决策的因素相互关系如图2、图3所示，通过分析PPP项目中政府补偿影响因素之间的关系，可为政府补偿作出决策提供参考。

(1)图2展示了影响政府作出补偿决策的因素并非是独立的，因素之间存在相关性，其中B和C之间的相关系数最高0.68，说明政府承受能力与社会资本方有很大的关系，如政府财政预算与社会资本方的投资回报率。若政府财政预算不平衡，对社会资本方的补偿受到影响,会使得社会资本方的投资回报率下降。

(2)从图3来看，五个一级指标的路径系数都达到了 0.6 以上，说明这五类因素对政府作出补偿决策起到关键的作用，在政府作出补偿决策时，应充分考虑五个方面的因素影响，使得政府补偿充分合理，避免考虑不充分导致项目失败，削弱社会资本方的积极性。

3.4.1 结构模型解释 (1)从表9的一级指标权重来看，五个一级指标中政府承受能力所占权重较大，为0.218。政府承受能力是衡量政府是否能对社会资本给予补偿的标准，也是保障社会资本方权益的基本条件，为了保证PPP项目的顺利执行，政府在作出补偿决策时应充分考虑自己的承受能力，采取政府承受能力论证等方式测算政府承受能力大小，保障PPP项目的顺利进行。

(2)其次权重最大的一级指标是工程项目因素，权重比值为0.205，说明工程项目因素在政府作出补偿决策时应重点考虑；政府对PPP项目补偿测算时，会考虑项目的营业收入以及运营成本，针对收益情况给予社会资本方补助，保障社会资本方的权益。

(3)外部环境的权重比值为0.2，政府在作出补偿决策时，应充分考虑到外部环境的影响。PPP项目周期长，应考虑政策制度的变更风险、折现率变化以及社会水平的变化等多种因素可能产生的后果；PPP项目投资额巨大，要考虑实际融资过程中融资成本的难度、超额投资成本的可能性等因素，从而做出合理的补偿决策。

(4)社会资本方以及社会公众的权重比值小，其中社会资本方权重比值为0.197，PPP项目中政府的补偿标准一般不是固定的，会根据社会资本方的绩效情况以及投资回报率，适当调整补偿标准，因此政府在作出补偿决策时应考虑社会资本方的实际情况；社会公众的权重最小，为0.179，比重最小，但在PPP项目政府补偿实施过程中，政府理应考虑社会公众的需求和承担能力，不应忽视社会公众的作用性。

3.4.2 测量模型解释 (1)在工程项目一级指标中，运营费用因素占一级指标权重为0.2638，所占权重最大，为影响主因，其次权重较大的预期营业收入所占比重为0.2020，在政府作出补偿决策时会充分考虑工程项目的实际运营费用以及预期营运收入，运营费用和预期营运收入决定了社会资本方的收益，社会资本方的收益不足，则政府提高补偿金额，弥补社会资本方的亏损，收益过高，则政府缩减补偿额。

(2)在政府承受能力指标中，政府的财政预算因素为关键影响因素，所占权重为0.2752。PPP项目入库后，政府将对PPP项目的补偿义务和付费纳入预算中，收支预算测算的不平衡性会使得PPP项目的财政支出超出政府的承受能力范围，因此政府应提高政府预算的准确性，促进PPP项目健康发展。

(3)在社会公众指标中，公众支付能力和付费意愿权重比较大，但是社会公众指标权重很小，综合考虑两者权重，其对政府作出补偿决策影响程度较小；在社会资本方指标中，绩效考核指标权重为0.5124，权重较大，政府会根据PPP项目的绩效评价结果，对社会资本方实施补偿策略。

(4)在外部环境指标中，PPP项目的超额投资风险和项目投资的偿还方式所占权重较大，均为0.1629。PPP项目执行周期长，投资额巨大，执行过程中各种不确定因素会造成投资额相对增多，例如机械设备的更新，使得重置成本发生变化，造成超额投资风险等；PPP项目中社会资本方所获收益来源是特许经营期的使用者付费亦或是政府出资补偿，政府在作出补偿决策时也应充分考虑这一点。

4 结论和讨论

本文对相关文献进行研究，通过灰色关联度法建立相应的指标体系并进行问卷调查，在考虑影响因素相关性的基础上，建立政府补偿影响因素的结构方程模型，对PPP项目中政府补偿决策的因素进行验证性分析，研究影响政府作出补偿决策的关键因素之间的关系以及重要程度，得到以下结论：

(1) 模型中权重系数和相关系数表明，PPP项目中政府作出补偿决策受到多种因素共同作用的影响，并且各个因素之间绝非独立存在的。

(2) 政府补偿决策影响因素的一级指标权重由大到小依次是政府承受能力、工程项目、外部环境、社会资本方和社会公众，较为重要的二级指标是政府财政预算、项目预期营业收入、运营费用和政府偿还能力。

(3) 通过建立结构方程模型解决了观测变量只能定性主观判断的缺点，将定性转化成定量，量化了影响因素之间的关系以及影响权重的大小。

在实际研究中，由于调查问卷样本数量和局限性较强，数据分布有不均匀现象且具有时效性，可能会使得所测结果与实际情况存在偏差，因此在未来数据模拟分析的发展上可以进一步研究。