基于改进核函数的支持向量机时间序列数据分类

李翔宇，李瑞兴，曾燕清

(1.闽江师范高等专科学校 计算机系，福建 福州 350108；2.物联网福建省高校应用工程中心，福建 福州 350108；3.福建江夏学院 电子信息科学学院，福建 福州 350108)

时间序列数据正在以一种难以想象的规模和速度快速增长，已经在商业、医药和科学研究等领域占据了大量的存储空间[1]。近年来，时间序列数据分类被广泛应用到很多的领域中，例如心电图ECG的模式匹配、手写识别、网络的入侵预测以及股市行情预测等。由于时间序列数据具有维度高、数据量大以及流数据等复杂特性，因此实际应用中时间序列数据分类面临了很多挑战。

由于时间序列数据在相同位置的数值一般不可直接比较，一般的分类算法不能直接应用于时间序列数据分类。为了解决这些问题，国内外的学者对时间序列数据分类进行大量的研究，并取得了很多有效的成果。原继东[2]等人通过计算原有时间序列与k个最好逻辑Shapelets的距离，将原有时间序列转换成新的拥有k个属性的数据，将时间序列分类问题转化成传统的分类问题。王志海[3]等人为每个待分类实例构建各自的数据驱动的懒惰式Shapelets分类模型，缩小了与其分类相关的时间序列搜索空间，并获得能够直接反映待分类实例的显著局部特征的Shapelets。王子一[4]等人通过k-shape聚类算法对子序列聚类，寻找两类时间序列数据中各自比较有区分性的片段，并以此来作为分类的依据。李海林[5]等人通过近邻传播算法对训练集数据进行聚类并寻找各类别的代表点，构建代表点的代表对象集，最后借助基于动态时间弯曲的均值中心方法对各代表对象集实现中心群计算，结合改进后的K近邻算法实现时间序列数据的分类。

支持向量机(SVM)[6-7]是 Vapnik 等人提出的一种建立在统计学习理论基础上的数据挖掘方法。在众多的机器学习算法中，支持向量机作为一种分类效果和稳定性较好的机器学习算法得到了广泛应用[8]。许多学者将SVM算法运用时间序列数据的分类工作中[9-10]，张坤华[11]等人针对多变量时间序列定义了每个属性的局部密度和判别距离，根据决策图的分布来筛选属性，最终通过SVM对数据进行分类。张振国[12]等人以子序列为单位，构建时序数据间的相似性向量，快速筛选出具有高分类能力的Shapelets集合，并使用SVM算法进行分类。传统的SVM算法一般应用于时间序列数据分类的最后阶段，即对降维或者转化操作后的时间序列数据进行分类。

针对时间序列数据的分类，传统的SVM算法仅通过样本在空间中的几何距离判别样本的类别，为此提出了一种基于改进核函数的支持向量机算法。首先计算样本与空间基数据的时间序列互相关距离，将样本数据映射到新的特征空间中，其次根据新特征空间的训练样本数据构建线性核函数的核矩阵，计算得到SVM的分类模型，最终根据该分类模型对新特征空间的测试样本数据进行分类获得分类结果。

1 SVM_IK算法

1.1 时间序列距离

1.1.1 时间序列

定义1(时间序列数据)：时间序列数据是一个有序的信息集合。时间序列X={x1,x2,Λ,xn}是一个长度为n的数据序列，其中数据序列的采样间隔为Δt=t(xi)-t(xi-1)。

定义2(空间基数据)：空间基数据是时间序列数据，主要应用于时间序列数据的特征空间转换。

定义3(类别时间序列数据)：类别时间序列数据是由定义1的时间序列数据与该时间序列数据的类别构成，D={(X1,y1),(X2,y2),Λ,(xn,yn)}，其中yi是时间序列Xi的类别。

1.1.2 时间序列互相关距离 在信号处理的流程中，常常用互相关函数来计算两个不同的波的相似性[13],因此可以将其应用于时间序列数据之间的相似性度量。让一个时间序列保持静止，另一个序列在静止序列上滑动，通过平移找到互相关的最大值，即为两个时间序列的相似性。对于时间序列数据x=(x1,x2,…,xm)与时间序列数据y=(y1,y2,…,ym)，序列x位移w个位置后与静止序列y的互相关函数如公式(1)所示：

(1)

其中w∈{-m,-m+1,Λ,0,Λ,m-1,m}，w≥0 时，表示x序列向右移动w个位置，w<0时，表示x序列向左移动w个位置，移动后空余的位置由0替代。

找到一个最优的位移w，使得C(x,y,w)的值最大，也就找到了x相对于y最好的位移。根据文献[14]的时间序列形状距离，时间序列互相关距离如定义4所示。

定义4(时间序列互相关距离)：衡量两个时间序列数据在形态上的一致性，时间序列x与序列y的互相关距离如公式(2)所示：

(2)

两个时间序列之间的互相关数值范围限定到[0,2]之间，即数值越大、越不相似，数值越小，越相似。

1.2 支持向量机(SVM)

支持向量机是基于统计学习理论( SLT) 的新型机器学习方法[12]。它是为了解决二分类识别问题而提出了方法，通过寻找一个最优的超平面，不仅能将训练样本正确分开，而且能使两类样本的分类间隔最大。

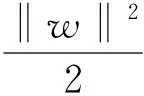
(3)

引入Lagrange函数来解决以上优化问题，如公式(4)：

(4)

其中λ≥0为拉格朗日乘子，通过对w和b求偏导，设置偏导为0，即可求解最优权值向量w*和最优偏置b*，分别如公式(5)和公式(6)所示：

(5)

b*=yi-∑yjλj(xj·xi)

(6)

由此可以获得最优的决策函数如公式(7)：

(7)

对于实际上难以线性分类的问题，可以将待分类数据射到某个高维的特征空间，并在该特征空间中构造最优分类面，从而转化成线性可分类问题。以高维空间的样本Φ(x)代替原样本数据x,则可以得到最优分类函数如公式(8)所示：

(8)

在高维特征空间构造最优超平面时，仅使用特征空间中的内积实现。可以通过一个核函数K(X,Xp)，如公式(9)所示：

(9)

则在特高维征空间建立超平面时无需考虑变换Φ的形式，简化映射空间中的内积运算。SVM的常用核函数有：Linear(线性)核函数、Polynomial(多项式)核函数、RBF(径向基)核函数和Sigmoid型核函数。

1.3 SVM_IK算法的步骤

SVM引入核函数的目的是将高维特征空间中大量的内积计算转换成低维空间简单的运算实现模型构建。不同的核函数蕴藏的几何度量特征各异，选择不同的核函数导致SVM泛化能力存在差异[15]。针对时间序列数据的分类，需要符合其特征的核函数对数据进行空间转换。

线性核函数作为SVM中的最简单的核函数，它并未对原始的数据元素进行空间转换。数据X=(x1,x2,…,xm)在线性核函数的公式中计算如公式(10)所示：

(10)

由于线性核函数中的几何度量特征不能有效的衡量时间序列数据的关系。为此，引入时间序列互相关距离，将时间序列数据映射到新的特征空间中，消除原始特征空间中数据的时间序列特性。通过空间基数据T=(t1,t2,…,tm)，对原始时间序列数据进行转换，得到新的特征空间数据，如公式(11)所示：

(11)

新的特征空间的数据不再具有原始时间序列特性，因此可使用线性核函数获得较好的SVM分类效果。将线性核函数与新的特征空间转换结合，改进的线性核函数如公式(12)：

k(X,X)=Dist(X,T)·Dist(X,T)

(12)

SVM_IK算法首先选用训练数据集作为空间基数据对训练数据进行空间转换，将空间转换映射后的结果进行构建相应的分类模型。其次将待分类的时间序列数据进行相应的空间转换，将空间转换后的结果输入到分类模型进行分类获得最终结果。SVM_IK算法的具体步骤如下：

步骤1：将时间序列数据集分为训练数据集Dtr(m×v)、训练标签集Ltr(m×1)、测试数据集Dte(n×v)、测试标签集Lte(n×1)，其中m为训练集样本个数，n为测试集样本个数，v为数据的维数；

步骤2：将训练集Dtr中的样本与空间基数据Dtr两两计算样本之间的时间序列互相关距离，构建m×m的新特征空间中的训练样本数据；

步骤3：将待分类数据集Dte中的样本与空间基数据Dtr两两计算样本之间的时间序列互相关距离，构建n×m的新特征空间中的待分类样本数据；

步骤4：使用线性核函数K(X,X)与训练标签集Ltr构建SVM分类模型Model 。

步骤5：构建n×m的新空间中的待分类样本数据输入到Model中进行分类，最终获得数据分类结果。

2 实验结果

实验采用编程语言为Python3.7，实验程序代码基于台湾林智仁教授等开发、设计的LibSVM[15]软件包基础上完成的。实验采用25组UCR数据集验证算法的有效性，UCR数据集是目前时间序列分类研究中普遍使用的数据集。

从表1可以看出，实验数据类型多样。类别从2类到60类，数据维度也是大小不一，最小60维，最长2000维；训练数据与测试数据的样本数量的差异也较大，因此可以更全面的衡量算法的性能。为了便于测试，实验数据集采用默认的训练数据和测试数据划分，以准确率作为分类结果评价指标。准确率定义如下:

准确率 = 正确分类的样本数/总样本数

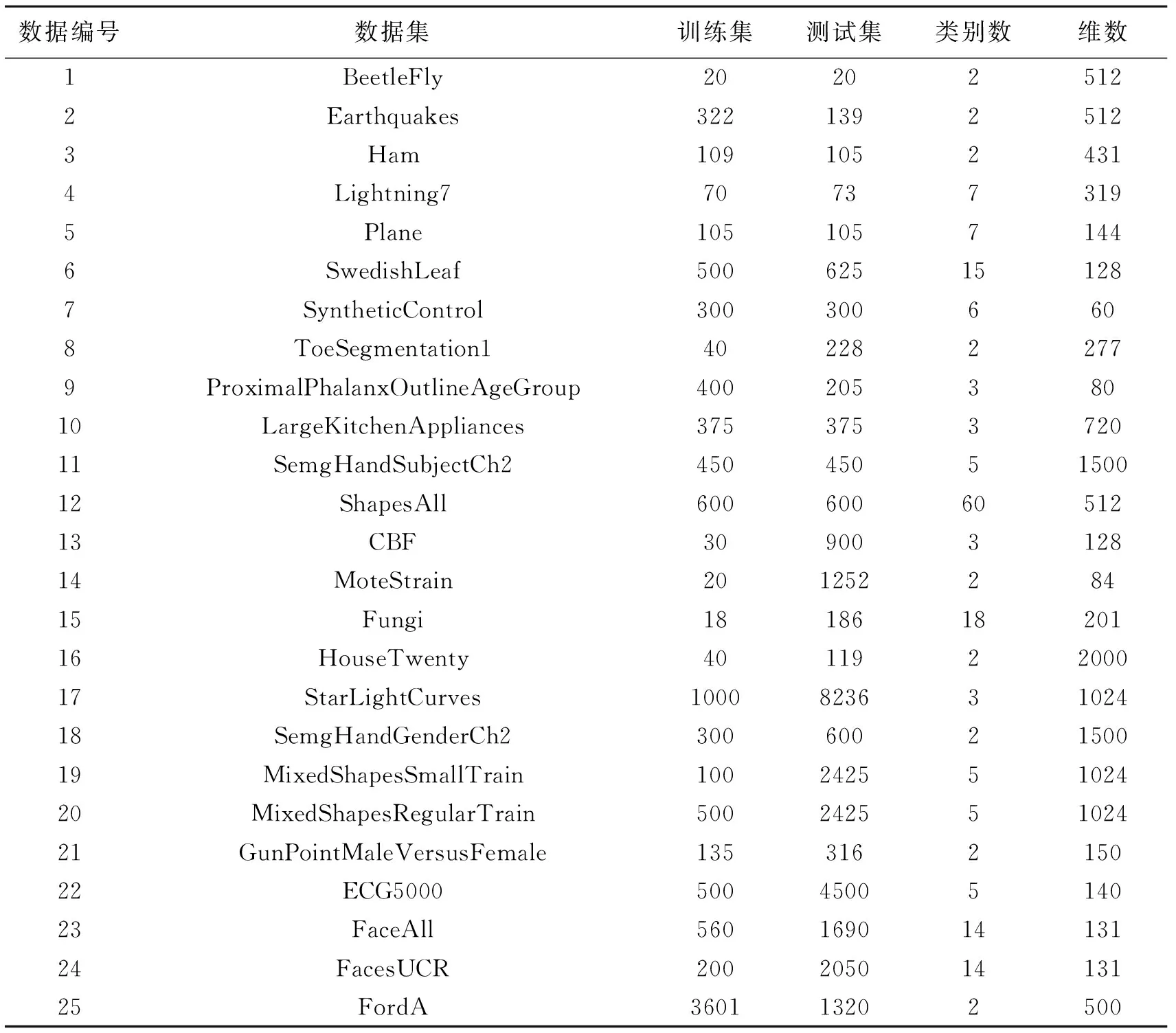
表1 25组UCR数据集

2.1 SVM_IK算法与传统SVM算法比较

实验中的对比算法采用基于Linear核函数、Polynomial核函数、RBF核函数、 Sigmoid型核函数下的SVM算法，实验中它们的简写分别为SVM_L、SVM_P、SVM_R和SVM_S。以上4种核函数的参数设置均采用libsvm中的默认参数，基于这些核函数的SVM算法分别对训练数据进行构建分类模型，最后通过构建的分类模型分别对测试数据分类，计算不同核函数下的准确率。SVM_IK算法对训练数据集构建分类模型，通过测试数据与训练数据的时间序列互相关距离构建的测试数据进行分类，计算最终的分类准确率。SVM_IK算法与4种不同核函数下的传统SVM算法实验对比图1和表2所示。

表2 与4种核函数下的SVM算法平均准确率对比

图1可知，基于RBF核函数、 Sigmoid型核函数的传统SVM算法对时间序列数据的分类效果较差，基于Linear核函数、Polynomial核函数的SVM算法则效果相当。SVM_IK算法仅8组数据的分类效果略低于这四种算法，其他17组数据的分类效果持平或者高于4种核函数下的SVM算法。

从表1中可以发现，SVM_IK算法的平均准确率均高于4种核函数下的SVM算法。由于传统的SVM算法采用的几何距离来衡量样本与超平面之间的距离，SVM_IK算法考虑到时间序列的形状上的相似度。

2.2 不同度量方式下的SVM_IK算法对比

SVM_IK算法采用时间序列互相关距离、DTW距离和欧氏距离下的改进算法分类效果，实验中采用简写为SVM_IK(R)、SVM_IK(ED)和SVM_IK(DTW)，它们的分类结果图2和表3所示。

表3 SVM_IK算法的三种度量下的平均准确率

从图2中可以发现，采用时间序列互相关距离时，18组数据的分类效果均好于其他两种度量，7组数据的分类效果略低于或持平于其他两种度量方式。同时表3中也可以发现采用时间序列互相关距离时，对于25组数据的平均分类准确率优于其他两种度量方式。也说明了 SVM_IK算法采用的时间序列互相关距离在分类过程中起到了积极的效果。

2.3 SVM_IK算法与1-NN算法对比

本实验对比SVM_IK算法与1-NN算法的分类结果，采用欧式距离度量的1-NN(ED)和采用DTW距离的1-NN(DTW)，对比结果如图3和表4所示。

表4 与1-NN算法平均分类准确率对比

图3中可以发现，与两种度量方式下的1-NN算法相比，SVM_IK算法有9组数据的分类效果略低于这他们两者，有2组数据的分类效果与其中一者持平，有14组数据的分类效果都高于这两者。通过表4可以发现本文算法的平均值均高于这两种度量下的1-NN算法。因此，本文提出的SVM_IK算法对时间序列数据分类能够有较好的分类准确率。

3 结论

时间序列数据分类在被广泛应用于很多领域中，很多学者把支持向量机应用于时间序列分类中。针对传统的支持向量机分类仅依据样本点在空间中的几何距离作为分类评判的依据，而没有考虑时间序列的数据形态特性，本文提出了SVM_IK算法引入了时间序列互相关距离，将时间序列的形态相似度引入到分类算法中，并对线性核函数进行相应的改进，使得支持向量机能够考虑样本形态上的相似性，在UCR数据集上获得较好的分类效果。