基于GWO-BP神经网络算法的WFGD系统在线优化

王 涛， 任少君， 司风琪， 马利君， 王力光

(1. 东南大学 能源热转换及其过程测控教育部重点实验室， 南京 210096； 2. 大唐环境产业集团股份有限公司特许经营分公司， 南京 210096)

近年来，随着国家对环保要求的不断提高，燃煤机组进行了超低排放改造。“十三五”规划中将SO2排放质量浓度限值从200 mg/m3降低至35 mg/m3。由于环保考核要求严格，为降低超标排放的风险，运行人员通常会选择多台浆液循环泵同时运行的方式，将SO2排放质量浓度控制在低于排放限值的安全区域内。这种运行方式使脱硫系统出口SO2质量浓度远低于国家规定的排放限值，大大增加了电厂脱硫系统的运行成本，降低了脱硫系统运行经济性，因此存在着很大的优化空间来节约电厂脱硫系统运行成本。

杨勇平等[1-3]通过机理分析方法对脱硫系统进行优化。然而，脱硫系统的实际运行状态受到多种因素(如机组负荷、煤质、锅炉燃烧方式等)的影响，难以通过一般的机理模型进行表化，因此数据驱动方法被广泛应用于脱硫系统的优化运行。QIAO Z L等[4-6]通过在稳定工况下对数据模型进行分析研究以优化脱硫系统的运行方式。

由于运行时外部条件在不断变化，脱硫系统很难长期处在稳定的运行状态，造成系统实际运行数据波动大，基于稳定的目标工况也很难给出可靠的优化方案[7]。在保证SO2排放质量浓度达标的前提下，笔者提出了一种灰狼优化(GWO)-BP神经网络建模方法，以浆液循环泵的运行情况作为工况划分条件，分别建立不同模态下的调度模型，构成针对石灰石-石膏湿法烟气脱硫(WFGD)系统的多模态在线优化模型组。通过该模型组预测运行浆液循环泵数量(即循环浆液量)对WFGD系统出口SO2质量浓度变化量的影响，从而实现对浆液循环泵的在线调度，达到降低脱硫系统运行成本的目的。此外，笔者对建模结果进一步进行分析，得到了机组负荷、入口SO2质量浓度对出口SO2质量浓度变化量的影响，并利用现场试验数据对该模型组的准确性进行了验证。

1 WFGD系统

WFGD技术是电站中应用最广泛的烟气脱硫技术，占总量的85%左右[8-9]。图1为WFGD系统工艺流程。锅炉排放的烟气经电除尘器和增压风机后，从吸收塔底部进入塔内。烟气在塔内自下而上流动，石灰石浆液从喷淋层喷出，从上往下滴落，两者逆向流动，在相互接触时，烟气中的SO2与石灰石浆液中的CaCO3发生化学反应生成CaSO3。生成的CaSO3落入塔底浆液池中，与H2O、O2反应生成CaSO4·2H2O[10-11]。而脱除SO2的净烟气经吸收塔顶部的除雾器除去烟气中的液滴后，通过烟囱排入大气。

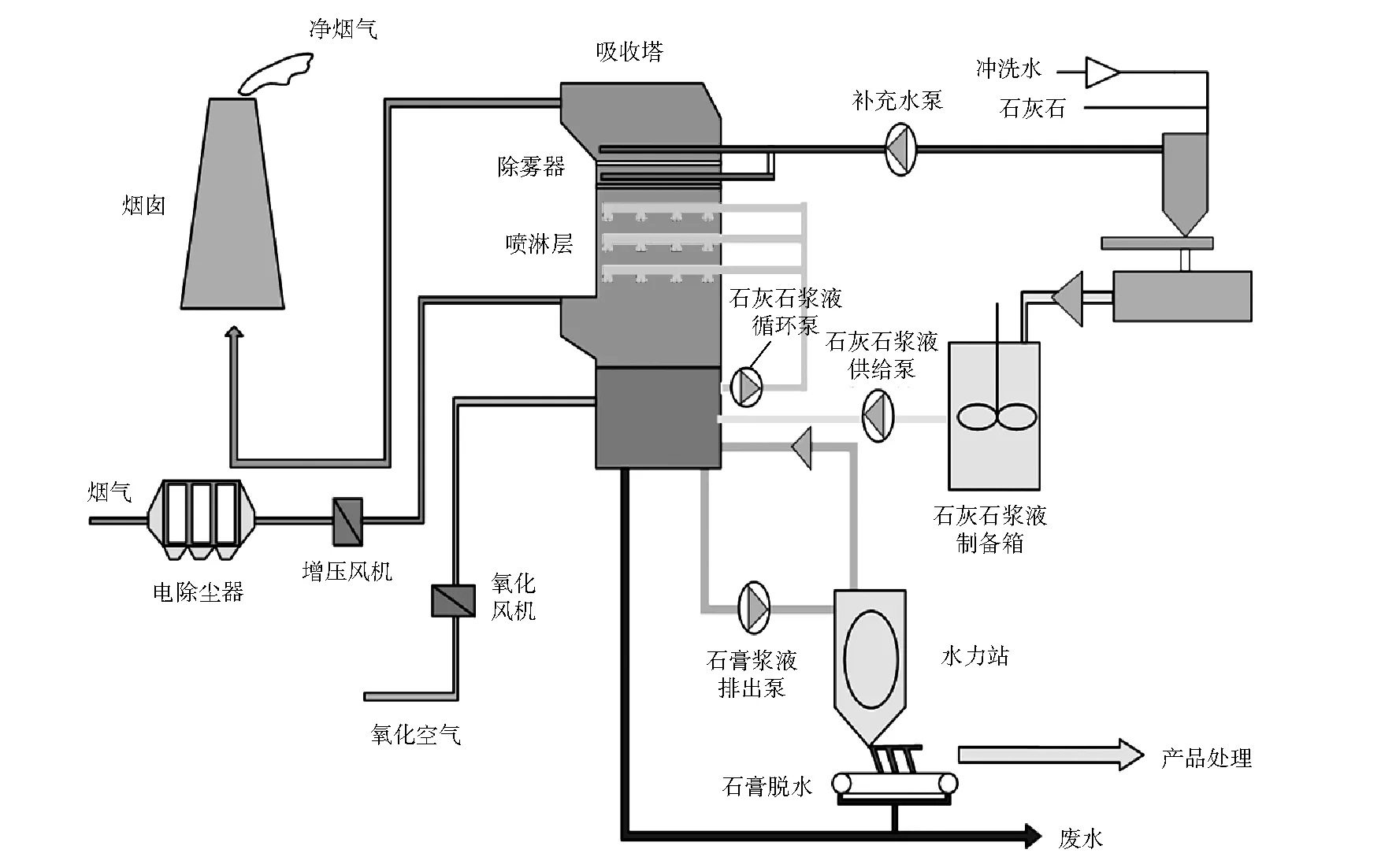
图1 WFGD系统工艺流程

由图1可得：WFGD系统以机组负荷、烟气流量、入口SO2质量浓度、出口SO2质量浓度(即SO2排放质量浓度)等参数为依据，通过控制运行浆液循环泵的数量来控制石灰石浆液供浆量。浆液循环泵作为WFGD系统核心设备，也是WFGD系统的耗电大户，其厂用电耗占比为0.7%～1.0%，耗电成本占WFGD系统总成本的60%～70%[12]。因此，采用合理的浆液循环泵运行策略可以大大降低电站脱硫成本。目前，燃煤机组WFGD系统还缺乏超低排放下浆液循环泵的运行规范，无法获得启停泵前后WFGD系统出口SO2质量浓度的变化情况，因此需要建立相应的出口SO2质量浓度变化量预测模型。

2 GWO-BP神经网络算法

2.1 BP神经网络

BP神经网络因具有简单的结构，可实现从输入到输出的任意非线性映射等特点[13]，成为目前应用最广泛的人工神经网络算法之一。BP神经网络是一种误差逆传播的多层前馈神经网络，其结构见图2，包括输入层、隐含层和输出层[14]。

BP神经网络具体计算步骤为：

(1) 随机初始化网络权重和偏置在0～1。

(2) 神经网络前向传播。

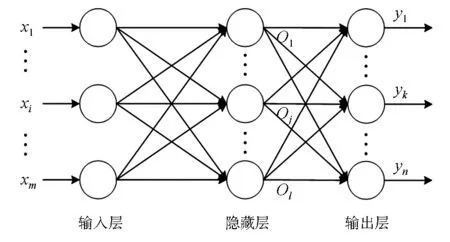
xi—输入层输入值(i=1,2，…，m，m为输入层个数)；Oj—隐藏层输出值(j=1,2，…，l，l为隐藏层个数)；yk—输出层输出值(k=1,2，…，n，n为输入层个数)。

图2 三层BP神经网络结构示意图

隐藏层和输出层输出计算公式为：

(1)

式中：f为Sigmoid激活函数[15]，f=1/(1+e-x)；wij为输入层输出侧各节点权重；θj为隐藏层输入侧各节点偏置；wjk为隐藏层输出侧各节点权重；θk为输出层输入侧各节点偏置。

(3) 神经网络反向传播。

定义神经网络的误差函数为：

(2)

误差函数对权重及偏置求偏微商可得：

(3)

式中：Δwjk、Δwij分别为wjk、wij的变化量；Δθk、Δθj分别为θk、θj的变化量。

对权值、偏置进行更新可得：

(4)

式中：ρ为学习率，0<ρ≤1。

(4) 若误差满足要求，则结束训练；若不满足，则重复步骤(2)和步骤(3)直至达到最大循环次数。

2.2 GWO算法

GWO算法[16]以自然界中灰狼的社会等级制度和狩猎行为为灵感，通过模拟狼群跟踪、追捕、包围、攻击猎物的过程，实现优化目标的目的。整个狼群按照适应度分为最优灰狼α(简称α狼)、次优灰狼β(简称β狼)、第三优灰狼δ(简称δ狼)和其他灰狼(简称ω狼)四个等级。通过计算灰狼个体与猎物间的距离，实现灰狼位置的更新，具体计算公式为：

(5)

式中：t为当前迭代次数；D为灰狼个体与猎物间的距离；XP为猎物的位置；X为灰狼个体的位置；A、C为系数向量，r1、r2为0～1的随机数组成的向量[17]；tmax为最大迭代次数；a为收敛因子[18]，随着迭代次数的增加，a从2线性减小到0。

种群内的其他个体依据α狼、β狼和δ狼的位置不断更新自己的位置，其计算公式为：

(6)

式中：Xα、Xβ、Xδ分别为α狼、β狼和δ狼的位置；Dα、Dβ、Dδ分别为灰狼个体与α狼、β狼和δ狼间的距离；X1、X2、X3分别为第t次灰狼个体向α狼、β狼和δ狼移动步长和方向的向量；A1、A2、A3和C1、C2、C3为α狼、β狼和δ狼移动的系数向量。

2.3 GWO-BP神经网络算法流程

BP神经网络在训练之前通常需要对训练样本进行归一化处理，将不同变量映射到相同的量级空间内。然而，在输入输出关系未知的情况下，盲目地对数据进行归一化处理，实际上就是认定不同输入变量对输出变量具有类似的影响程度，这显然是不合理的。因此，笔者提出了一种基于GWO-BP神经网络的建模方法，通过优化参数训练权重，区分输入变量对输出变量影响程度的差异性，进一步提高BP神经网络的预测精度，并找出对输出变量影响最大的关系变量。

GWO-BP神经网络算法流程见图3(R2为衡量预测结果精度的指标)。

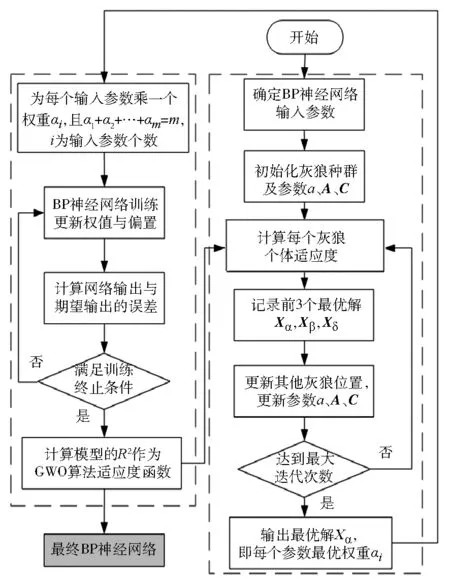
图3 GWO-BP神经网络算法流程图

GWO-BP神经网络算法的具体步骤如下：

(1) 确定BP神经网络的输入和输出参数，并对输入和输出数据进行归一化处理。

(2) GWO算法种群初始化。随机初始化灰狼种群位置Xz(z=1，2，…，Z，Z为灰狼种群数)，每个灰狼个体包含一组权重αi(α1+α2+…+αm=m)，初始化参数a、A、C。

(3) 构造适应度函数。归一化后的每个输入变量乘上对应的权重作为新的输入参数，并对BP神经网络进行训练，利用模型预测输出数据与期望输出数据计算所得的R2构造适应度函数，R2的计算公式为：

(7)

(4) 对种群中的每个灰狼个体执行BP神经网络训练，并通过式(7)计算每个灰狼个体的适应度，从中选出适应度最高的3个灰狼，作为当前的最优解Xα、次优解Xβ和第三优解Xδ。

(5) 根据式(6)和式(7)更新ω狼个体的位置，更新参数a、A、C。根据步骤(3)所述重新构造新的BP神经网络，并对网络进行训练，重新计算每个灰狼个体的适应度，更新Xα、Xβ和Xδ。

(6) 判断GWO算法是否达到最大迭代次数。若是，则停止迭代，并输出最优结果Xα；反之，则重复执行步骤(3)～步骤(5)，直至达到最大迭代次数。

(7) 利用GWO算法得到的最优输入变量的权重再次训练BP神经网络，可得到训练精度最高的BP神经网络模型，并将其作为最终模型。

3 WFGD系统在线优化

为了实现对浆液循环泵的在线调度，从而达到降低WFGD系统运行成本的目的，笔者以运行浆液循环泵台数划分工况，建立基于GWO-BP神经网络的WFGD系统在线优化调度模型组合，图4为基于GWO-BP神经网络的WFGD系统在线优化调度方法流程。

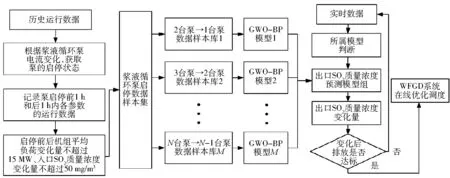
图4 基于GWO-BP神经网络的WFGD系统在线优化调度方法流程

该方法具体步骤如下：

(1) 依据浆液循环泵电流参数，判断浆液循环泵的运行状态。记录只有单台浆液循环泵启停的时刻，并记录该时刻前后各1 h内相关参数的历史运行数据。

(2) 由于机组负荷多变及配煤掺烧等因素影响，WFGD系统常在不同工况下运行。除此之外，由于笔者研究浆液循环泵运行台数与出口SO2质量浓度变化量的关系，在选择建模样本时，需要保证浆液循环泵启停前后机组负荷和入口SO2质量浓度基本保持稳定，排除其他因素对建模结果造成干扰，从而提高模型的准确度与精度。因此，需要对获得的数据样本进行稳态筛选。稳态筛选条件为：浆液循环泵启停前后机组平均负荷变化量不超过15 MW、入口SO2质量浓度变化量不超过50 mg/m3，最终获得浆液循环泵启停数据样本集。

(3) 按照浆液循环泵运行情况，将数据样本划分到相应的样本库中，并采用GWO-BP神经网络建模方法，分别建立WFGD系统在线优化调度模型，其输入输出参数的模型结构见图5。采用出口SO2质量浓度变化量代替实际出口SO2质量浓度作为模型的输出参数，该方法能够有效提高模型的可靠性和应用性，更能直观地反映出切换浆液循环泵后对出口SO2质量浓度变化的影响。

图5 WFGD系统的GWO-BP神经网络模型结构

(4) 通过切换浆液循环泵的运行台数，判断机组实时运行数据所属的模型类别。通过建立的模型组进行预测，可得到当前时刻切换单台浆液循环泵后出口SO2质量浓度的变化量。若变化后的出口SO2质量浓度符合国家排放标准，则可达到对WFGD系统浆液循环泵进行在线优化调度的目的，并为电站浆液循环泵的运行提供参考。

4 应用分析

笔者选取某660 MW燃煤机组WFGD系统作为建模对象，该系统按一炉一塔方式布置，配备4台浆液循环泵。

表1为该电站超低排放改造后SO2排放质量浓度在不同区间内机组的运行时间占比。

表1 机组的运行时间占比

由表1可得：SO2排放质量浓度在0～<20 mg/m3的机组运行时间约占总运行时间的70%，在大部分运行时间内，SO2排放质量浓度远低于国家规定的排放限值，存在很大的优化空间来节约电厂脱硫系统运行成本。因此，笔者利用提出的GWO-BP神经网络建模方法，针对该机组建立WFGD系统在线优化调度模型组。

4.1 数据准备

通过电厂厂级监控信息系统(SIS)，获取该机组5个月的WFGD系统运行数据，采样间隔为1 min。依据浆液循环泵电流参数，获取启停单台浆液循环泵时的各时间节点，以及启停前后各1 h的运行数据。去除机组启停机、SIS测点失效参数等数据，共获得236个样本。

从获得的数据中，依据浆液循环泵启停前后的运行数量，筛选出4台泵切换到3台泵及3台泵切换到2台泵的数据样本。由于2台泵切换到1台泵的样本较少，且1台泵的额定体积流量为9 880 m3/h，在机组正常运行和超低排放前提下，出口SO2质量浓度无法满足国家规定的环保排放标准，故不考虑该情况。对建模所需的数据样本进行稳态筛选，切换前后的运行数据见图6、图7。

图6 4台泵切换到3台泵前后机组的运行数据

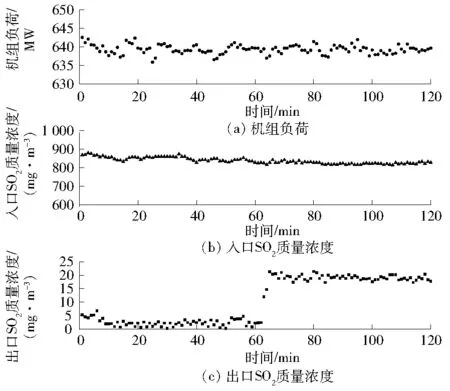
图7 3台泵切换到2台泵前后机组的运行数据

最终获得4台泵切换到3台泵的运行数据共60组，以及3台泵切换到2台泵的运行数据共55组。计算每组样本切换前后机组负荷、入口SO2质量浓度、切换前出口SO2质量浓度及切换后出口SO2质量浓度的变化量(正值表明SO2质量浓度升高)，部分运行数据见表2。

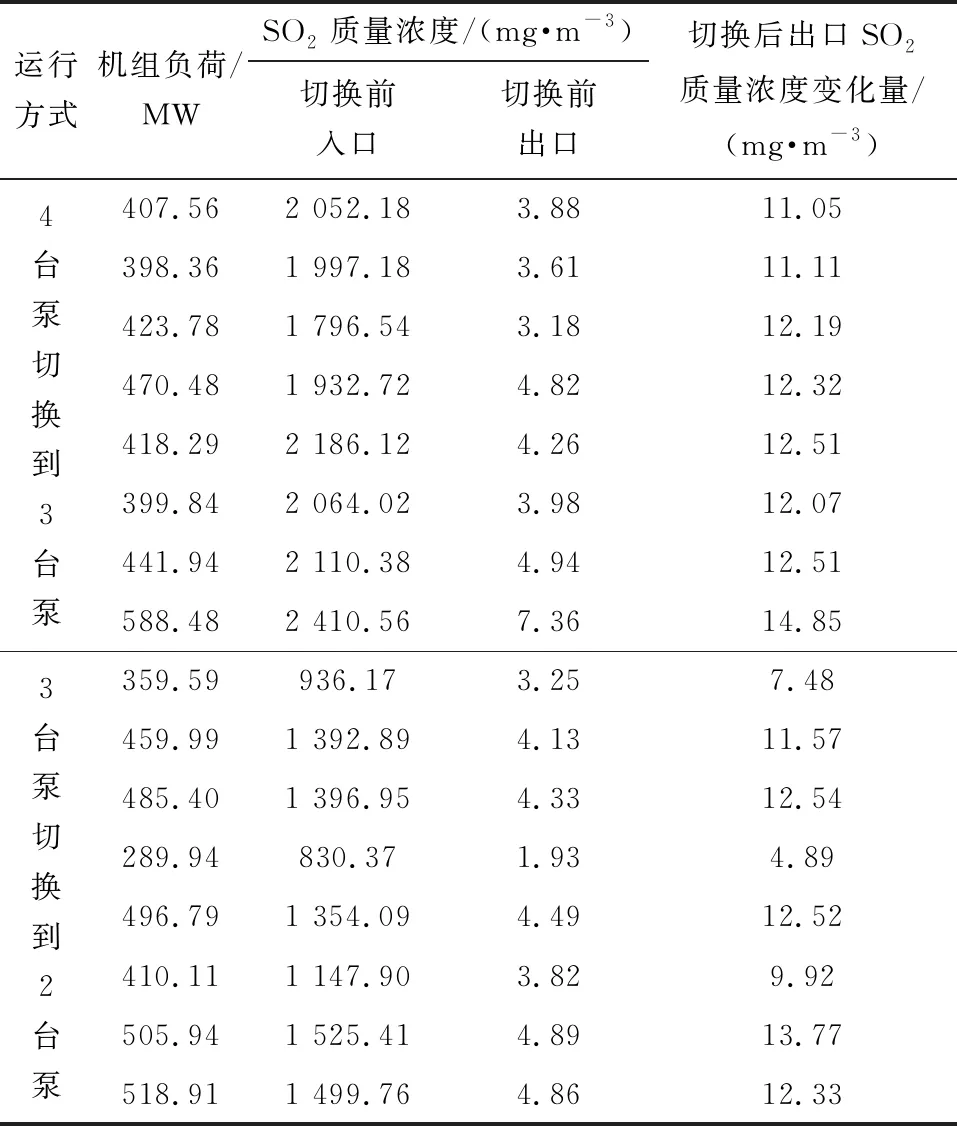
表2 切换前后机组的部分运行数据

由于输入变量和输出变量的量纲不同，直接对模型进行训练会大大降低模型收敛速度和精度，影响模型的预测效果。因此，在训练模型前，采用Min-Max归一化方法对样本数据进行归一化处理，使输入输出数据规范在0～1。

4.2 模型建立

分别利用GWO-BP神经网络建模方法和传统BP算法，建立4台泵切换到3台泵、3台泵切换到2台泵的模型。选取70%样本作为模型的训练样本，剩下数据作为模型的测试样本。通过试验调整，最终确定BP神经网络隐含层数为8，学习率为0.001，最大迭代次数为3 000，训练精度为10-7。设置GWO算法初始种群规模为30，迭代次数为200。通过GWO算法寻优所得的输入参数权重分别为1.18、1.24、0.58，同时也说明机组负荷与入口SO2质量浓度对输出参数的影响较大。

基于GWO-BP神经网络模型和传统BP神经网络模型的训练结果和测试结果见图8(4台泵切换到3台泵)和图9(3台泵切换到2台泵)。由图8和图9可得：基于GWO-BP神经网络模型的拟合效果明显优于传统BP神经网络模型，说明笔者提出的基于GWO-BP神经网络模型具有更好的预测效果。

图8 4台泵切换到3台泵的模型训练和测试结果

图9 3台泵切换到2台泵的模型训练和测试结果

同时，为了定量评价模型性能，采用均方根误差和平均相对误差对模型的精度进行评价。均方根误差和平均相对误差越小，表明预测越准确，模型拟合效果越好。

(8)

(9)

式中：ERMSE为均方根误差；EMRE为平均相对误差。

两种建模方法针对出口SO2质量浓度变化量的结果对比见表3。由表3可得：基于GWO-BP神经网络模型比传统BP神经网络模型有更好的拟合效果。

表3 两种建模方法的结果对比

4.3 结果分析

通过建立的基于GWO-BP神经网络的WFGD系统在线优化调度模型组，研究在其他输入条件不变的情况下，单独改变某个输入参数，出口SO2质量浓度变化量的变化情况。同时，为了验证该模型组的预测性能，将其运用于该机组WFGD系统，研究模型预测结果与实际运行结果的吻合情况。

4.3.1 机组负荷的影响

保持WFGD系统出口SO2质量浓度不变(5 mg/m3)，改变机组负荷，负荷间隔为25 MW，通过模型预测得到的结果见图10。

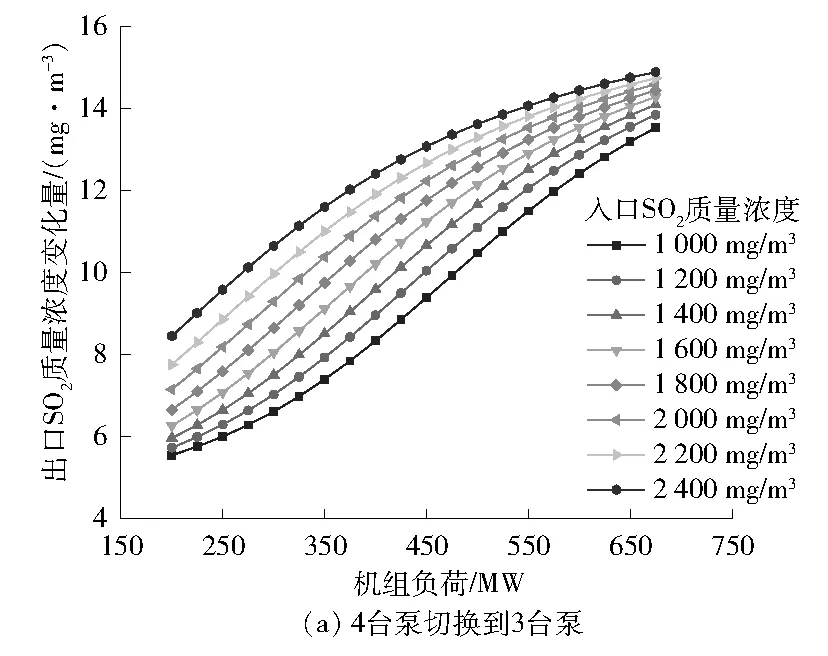
图10 机组负荷对出口SO2质量浓度变化量的影响

由图10可得：关闭1台浆液循环泵后，随着机组负荷增大，出口SO2质量浓度变化量逐渐增大；并且入口SO2质量浓度越大，出口SO2质量浓度变化量越大。

实际脱硫过程中，在入口SO2质量浓度不变的前提下，随着机组负荷的增大，烟气量也随之增加，直接体现在液气比nLG的变化，其计算公式为：

nLG=qm,L/qm,G

(10)

式中：qm,L为循环浆液的质量流量；qm,G为吸收塔通过烟气的质量流量。

脱硫效率随液气比增大而增大，并且当液气比较小时，增加液气比能更有效地提高脱硫效率[19]。此外，从式(10)可看出：在循环浆液质量流量一定时，随着机组负荷增大，吸收塔通过烟气的质量流量增加，因此液气比逐渐减小。在高负荷时液气比较小，所以在高负荷段，切换泵引起的脱硫效率变化更大，因此出口SO2质量浓度变化量随负荷增大而增大，模型所得结果与实际情况基本吻合。

4.3.2 入口SO2质量浓度的影响

保持出口SO2质量浓度一定(5 mg/m3)，改变入口SO2质量浓度，入口SO2质量浓度间隔为50 mg/m3，通过模型预测得到的结果见图11。

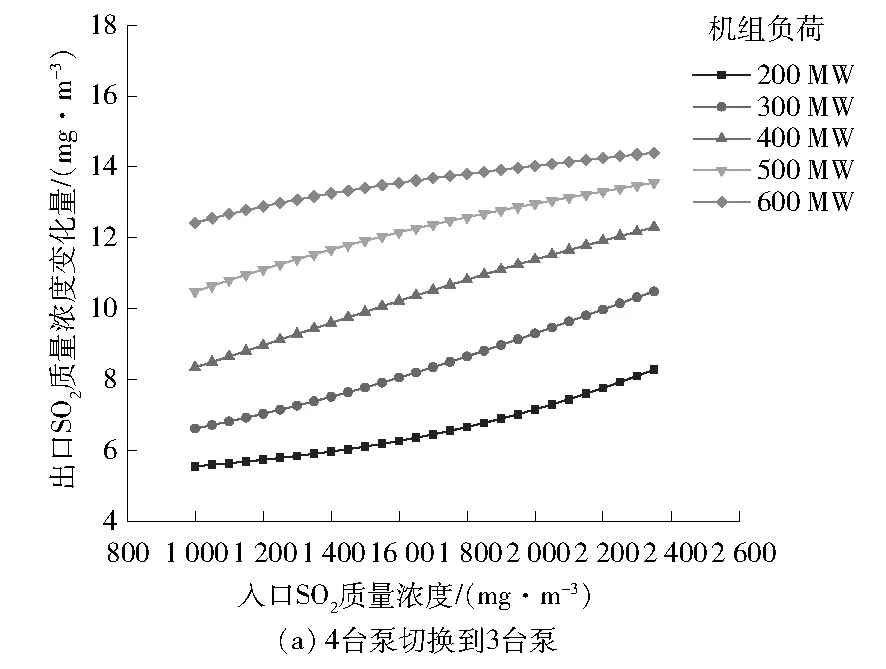
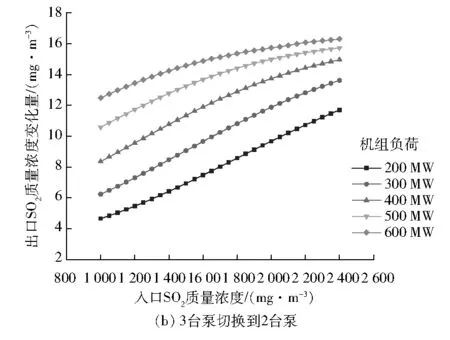
图11 入口SO2质量浓度对出口SO2质量浓度变化量的影响

由图11可得：关闭1台浆液循环泵后，随着入口SO2质量浓度的增大，出口SO2质量浓度变化量呈现出增大的趋势；并且随着机组负荷增大，出口SO2质量浓度变化量减小。这是因为入口SO2质量浓度增大时，为了保持出口SO2质量浓度不变，每台泵需要脱除SO2的量增加。关闭1台浆液循环泵后，出口SO2质量浓度的增加量即为关闭的该台浆液循环泵SO2的脱除量。因此，当关闭1台浆液循环泵后，系统出口SO2质量浓度变化量随着入口SO2质量浓度的增大而增大，模型预测结果与实际运行情况基本吻合。

4.4 现场试验验证

为了验证模型组的预测性能，对该机组进行了相关浆液循环泵切换试验，并将试验验证结果与模型结果进行对比，得到结果见表4。由表4可得：试验验证结果与模型预测结果的绝对误差不超过1.5 mg/m3。这说明该模型的预测精度较高，能够较好地预测切换后WFGD系统出口SO2质量浓度的变化情况，满足实际工程中对出口SO2质量浓度变化情况的预测需求。

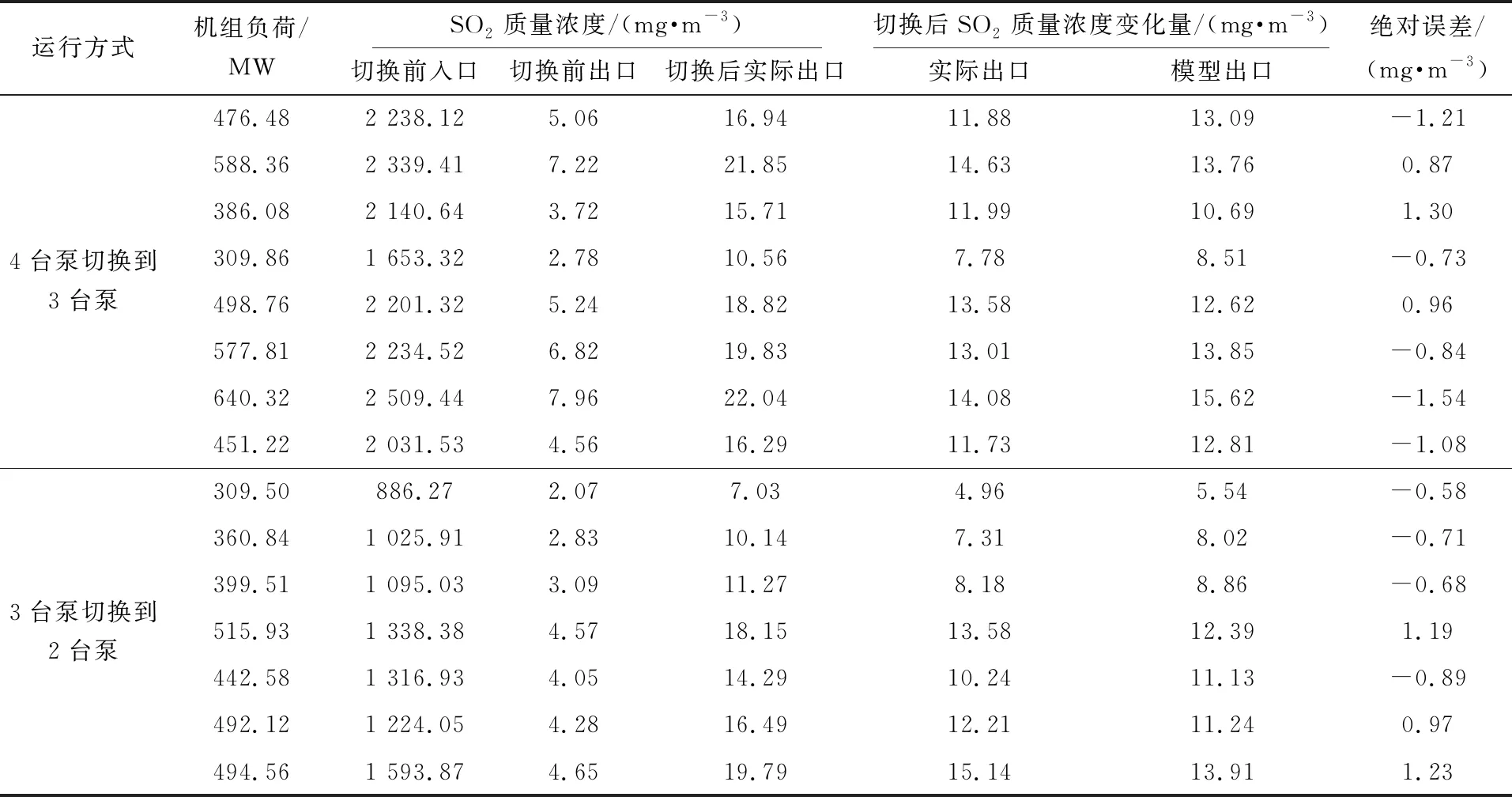
表4 切换前后试验结果与模型预测结果对比

5 结语

笔者提出了一种针对WFGD系统的在线优化调度方法，通过获取某机组浆液循环泵切换数据，建立了基于GWO-BP神经网络算法的脱硫系统出口SO2质量浓度变化量预测模型组，并对预测结果进行了分析，得出以下结论：

(1) 笔者提出的基于GWO-BP神经网络模型比传统BP神经网络模型具有更好的预测效果。

(2) 在模型其他输入参数不变的条件下，切换浆液循环泵后WFGD系统出口SO2质量浓度的变化量随着机组负荷的增大而逐渐增大，且随着入口SO2质量浓度的增大而逐渐增大。

(3) 基于GWO-BP神经网络模型组的预测结果与实际情况基本吻合，预测精度较高，因此该模型可为WFGD系统在线优化调度提供参考。